| Repeat L iterations of Steps 1–6: | ||
| Step 1: Generate Y1 ~ f(Y1 | x1, θ̄12) | ||
| Repeat for i = 2, …, M: | ||
| Step 2: Evaluate g(xi | Y1, …, Yi−1, xi, …, xi−1, θ̄12). If g(·) is a deterministic function (as in dose allocation), record the value as xi. If g(·) is a non-degenerate distribution generate xi accordingly. | ||
| Step 3: Generate Yi ~ f(Yi | Y1, …, Yi−1, xi, θ̄12), using xi from Step 2. | ||
Step 4: The vector
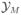 = (Y1, …, YM) is a simulated outcome vector. = (Y1, …, YM) is a simulated outcome vector. | ||
Step 5: Evaluate the posterior variance covariance matrix Σ(θ |
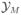 ). This evaluation might require Markov chain Monte Carlo integration when the model is not conjugate. ). This evaluation might require Markov chain Monte Carlo integration when the model is not conjugate. | ||
Step 6: Evaluate det(Σ−1(
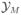 )). )). | ||
| Step 7: The average over all L iterations of steps 1 through 6. | ||
| ||
approximates the desired integral. The sum is over the L repeat simulations of Steps 1 through 6, plugging in the vector
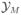 that is generated in each step of the simulation. that is generated in each step of the simulation. |

An official website of the United States government
Here's how you know
Official websites use .gov
A
.gov website belongs to an official
government organization in the United States.
Secure .gov websites use HTTPS
A lock (
) or https:// means you've safely
connected to the .gov website. Share sensitive
information only on official, secure websites.