Repeat L iterations of Steps 1–6:

Step 1: Generate Y1 ~ f(Y1 | x1, θ̄12)

Repeat for i = 2, …, M:

Step 2: Evaluate g(xi | Y1, …, Yi−1, xi, …, xi−1, θ̄12). If g(·) is a deterministic function (as in dose allocation), record the value as xi. If g(·) is a non-degenerate distribution generate xi accordingly.

Step 3: Generate Yi ~ f(Yi | Y1, …, Yi−1, xi, θ̄12), using xi from Step 2.

Step 4: The vector 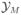= (Y1, …, YM) is a simulated outcome vector.

Step 5: Evaluate the posterior variance covariance matrix Σ(θ | 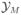). This evaluation might require Markov chain Monte Carlo integration when the model is not conjugate.

Step 6: Evaluate det(Σ−1( )).

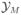Step 7: The average over all L iterations of steps 1 through 6.

$$\frac{1}{L}\sum det({\mathrm{\sum }}^{-1}({\mathcal{Y}}_M))\approx \int det\{{\mathrm{\sum }}^{-1}({\mathcal{Y}}_M)\}{f}_M({\mathcal{Y}}_M\mid {\overline{\mathit{\theta }}}_{12}){dY}_M,$$ (16)

approximates the desired integral. The sum is over the L repeat simulations of Steps 1 through 6, plugging in the vector 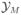that is generated in each step of the simulation.