The working stroke of the myosin II motor in muscle is not tightly coupled to release of orthophosphate from its active site

Abstract

Skeletal muscle shortens faster against a lower load. This force–velocity relationship is the fundamental determinant of muscle performance in vivo and is due to ATP-driven working strokes of myosin II motors, during their cyclic interactions with the actin filament in each half-sarcomere. Crystallographic studies suggest that the working stroke is associated with the release of phosphate (P_i) and consists of 70 deg tilting of a light-chain domain that connects the catalytic domain of the myosin motor to the myosin tail and filament. However, the coupling of the working stroke with P_i release is still an unsolved question. Using nanometre–microsecond mechanics on skinned muscle fibres, we impose stepwise drops in force on an otherwise isometric contraction and record the isotonic velocity transient, to measure the mechanical manifestation of the working stroke of myosin motors and the rate of its regeneration in relation to the half-sarcomere load and [P_i]. We show that the rate constant of the working stroke is unaffected by [P_i], while the subsequent transition to steady velocity shortening is accelerated. We propose a new chemo-mechanical model that reproduces the transient and steady state responses by assuming that: (i) the release of P_i from the catalytic site of a myosin motor can occur at any stage of the working stroke, and (ii) a myosin motor, in an intermediate state of the working stroke, can slip to the next actin monomer during filament sliding. This model explains the efficient action of muscle molecular motors working as an ensemble in the half-sarcomere.

Key points

• Force and shortening in muscle are caused by ATP-driven working strokes of myosin II motors, during their cyclic interactions with the actin filament in each half-sarcomere. Crystallographic studies indicate that the working stroke consists in an interdomain movement of the myosin motor associated with the release of inorganic phosphate (P_i).

• Here the coupling of the working stroke with the release of P_i is studied in situ using fast half-sarcomere mechanics on skinned fibres from rabbit psoas.

• The isotonic velocity transient following stepwise force reductions superimposed on isometric contraction measures the mechanical manifestation of the working stroke and its rate of regeneration.

• The results indicate that the release of P_i from the catalytic site of an actin-attached myosin motor can occur at any stage of the working stroke, and a myosin motor uses two consecutive actin monomers to maximize the power during shortening.

Introduction

In the muscle cell, steady force and shortening are generated by the two bipolar arrays of the motor protein myosin II emerging from the myosin filament and pulling the actin filaments towards the centre of the sarcomere during cyclical ATP-driven interactions. Being part of a collective motor, sarcomeric myosin II has evolved specific mechano-kinetic properties to maximize power and efficiency, that are still not fully defined and can be investigated only by preserving the three-dimensional lattice organization of the myofilaments.

Sarcomere-level mechanics and X-ray interferometry in single intact fibres from frog skeletal muscle have provided most of the information about the number and conformation distribution of the myosin motors as they perform different physiological tasks (Piazzesi et al. 2007). In agreement with earlier evidence obtained with electronic paramagnetic resonance spectroscopy in skinned rabbit fibres (Cooke et al. 1982), no more than 30% of all motors in a myosin half-filament are attached to actin during isometric contraction. During shortening against high and moderate loads, the number of myosin motors reduces in proportion to the sarcomere load, so that individual myosin motors maintain a force similar to the isometric force F₀, pulling the actin filament through a 6 nm stroke, which is about one-half of that suggested by crystallographic models (Rayment et al. 1993; Geeves & Holmes, 2005). These results are consistent with a model of the motor action where power and efficiency are maximized by (i) a rapid conformation-dependent detachment from actin that keeps low the resistive load exerted by the motors at the end of the working stroke (Piazzesi et al. 2007) and (ii) a rate of repriming of the working stroke during shortening at high and moderate load (as measured by the rate of recovery of the ability to execute a second working stroke in the double step release experiment) that is faster than expected from the ATPase rate (Irving et al. 1992; Lombardi et al. 1992, 1995). Using sarcomere level mechanics in demembranated muscle fibres, which allow the control of the chemical composition of the solution bathing the myofilaments, we showed that when the concentration of inorganic phosphate (P_i) is increased the number of motors attached to actin during isometric contraction decreases in proportion to the reduction of force (Caremani et al. 2008), much more than expected from the decrease of the ATPase rate (Bowater & Sleep, 1988; Pate & Cooke, 1989b; Potma & Stienen, 1995, 1996). This finding suggested that during isometric contraction the myosin motor can detach from actin with the hydrolysis products (P_i and ADP) still bound to its catalytic site and re-enter the cycle following rapid release of ligands and rebinding of ATP (Linari et al. 2010; Caremani et al. 2011). This sort of unconventional ATPase cycle, however, cannot per se explain the high power of shortening muscle, because the attachment step is rate limited by ATP hydrolysis (Bagshaw & Trentham, 1974; White & Taylor, 1976; Sleep et al. 2005).

To investigate how the myosin motor, as a part of the collective half-sarcomere motor, can maximize muscle power by increasing the rate of repriming of the working stroke during shortening, we apply here fast sarcomere-level mechanics to demembranated fibres, and record the isotonic velocity transient (Podolsky, 1960; Huxley, 1974; Piazzesi et al. 2002) following a step reduction in force from the isometric force T₀ (see Fig. 1) and its modulation by an increase in the concentration of P_i. The power of this approach derives from the fact that, following the elastic (phase 1) response, the multiphase shortening elicited by the force step occurs under isotonic conditions and thus the half-sarcomere elastic components do not change their length and the shortening depends solely on the action of the ensemble of myosin motors acting in parallel in the half-sarcomere (Piazzesi et al. 2002, 2007; Reconditi et al. 2004). The early rapid shortening (phase 2), complete within few milliseconds, is the mechanical manifestation of the working stroke in the attached motors, synchronised by the drop in force, and the following reduction or pause in shortening velocity (phase 3) is due to synchronised motor detachment preceding the cyclic motor attachment–detachment, accounting for the steady shortening velocity (phase 4). This approach is superior to the use of single molecule mechanics for measuring the kinetics of a rapid non-processive motor like myosin II. Even the recent most sophisticated approach (Capitanio et al. 2012), consisting in the application of a constant resistive load between the actin filament and the myosin motor in the three bead assay configuration, proved to be too far from physiological conditions, giving estimates of the rate of the myosin detachment at the end of the working stroke (∼200 s⁻¹) one order of magnitude slower than that measured in situ at the same low load (1000–2000 s⁻¹ (Piazzesi et al. 2007), due to the low ATP concentration required for recording single events by increasing their lifetime.

Figure 1. Isotonic velocity transient following a step in force to 0.5 T₀ superimposed on the isometric contraction.

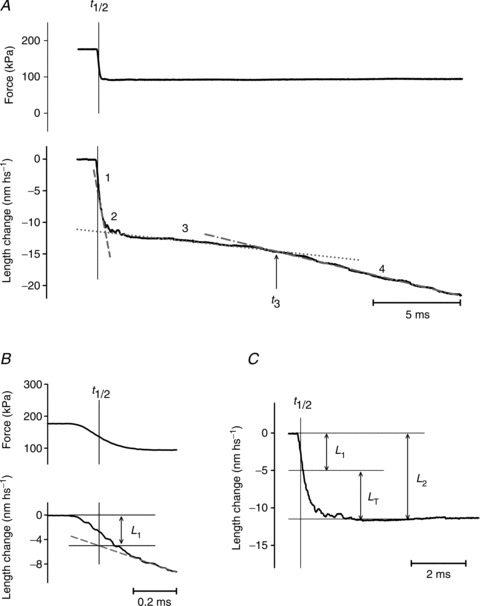
A, shortening of the half-sarcomere (lower trace) in response to the step to 0.5 T₀ (upper trace). Numbers above the shortening record identify the phases of the transient; t₃ marks the transition between phases 3 and 4. B and C, early components of the shortening showing the method for estimating L₁ and L₂. L₁ is measured by extrapolating the tangent to the initial part of phase 2 response (dashed line in A and B) back to the half-time of the force step (t_½, indicated by the vertical line). L₂ is measured by extrapolating the ordinate intercept of the tangent to the phase 3 response (dotted line in A) back to t_½, to suppress the small contribution of phase 3. Alternatively, as shown in C, the whole time course of phase 2 shortening leading to L₂ is calculated by subtracting the phase 3 tangent from the record starting from t_½. L_T, the size of the working stroke, is obtained by subtracting the elastic response L₁ from L₂. Steady shortening velocity is estimated from the slope of the tangent to phase 4 response (dotted–dashed line in A). Fibre segment length, 3.3 mm; segment length under the striation follower, 1.0 mm; average sarcomere length, 2.51 μm; CSA, 3780 μm²; temperature, 11.8°C.

With respect to the complementary method of imposing a length step to elicit the force transient (Huxley & Simmons, 1971), the force step method has the advantage that the rate of phase 2 shortening occurs under isotonic conditions and thus is the direct expression of the strain-dependent kinetics of the working stroke, without any influence of filament compliance (Reconditi et al. 2004; Linari et al. 2009).

We find that the speed of the early rapid shortening in phase 2 of the velocity transient following the force drop to the same value relative to the isometric force is not affected by [P_i], while the pause in phase 3 is briefer and the steady shortening velocity is increased. The results are interpreted in terms of a chemo-mechanical model of the myosin motor that integrates a kinetic model able to simulate the P_i dependence of isometric force and ATPase rate (Linari et al. 2010) with the Huxley–Simmons model of the working stroke (Huxley & Simmons, 1971), which implies strain-dependent transitions between different states of the attached motors. We conclude that: (i) the execution of the working stroke and the release of hydrolysis products by a force-generating myosin motor are orthogonal events; namely, first P_i and then ADP may be released at any stage of the strain-dependent conformational change in the motor, though progression in the working stroke increases the rate constants of product release; (ii) during steady shortening and power production a myosin motor with both ligands or only ADP in its catalytic site can slip from the original actin monomer to the next actin monomer farther from the centre of the sarcomere, while the actin filament slides along for the action of the other attached motors. In this way the free energy of the ATP hydrolysis remaining from the interaction with the first actin supports further work on the second actin, which is how the sarcomeric myosin, as a part of a collective motor, maximizes muscle power and efficiency.

Methods

Fibre mounting and mechanical apparatus

Experiments were done on glycerinated skinned fibre segments from psoas muscles of adult male New Zealand white rabbits (3–5 kg). Rabbits were killed by injection of an overdose of sodium pentobarbitone (150 mg kg⁻¹) in the marginal ear vein, in accordance with the official regulations of the Community Council (Directive 86/609/EEC) and with Schedule 1 of the UK Animals (Scientific Procedures) Act 1986. The study was approved by the Ethical Committee for Animal Experiments of the University of Florence. Small bundles (70–150 fibres) were stored in skinning solution containing 50% glycerol at –20 °C for 3–4 weeks and single fibres were prepared just before the experiment as previously described (Goldman et al. 1984; Linari et al. 2007). A fibre segment 5–6 mm long was cut from the fibre and T-shaped aluminium clips were mounted at its extremities for attachment between the lever arms of a loudspeaker motor and a capacitance force transducer with resonant frequency 40–50 kHz (Lombardi & Piazzesi, 1990 and references therein). The two ends of the fibre were fixed with glutaraldehyde in rigor solution and glued to the clips with shellac dissolved in ethanol. Sarcomere length (l_s), width (w) and height (h) of the fibre were measured at 0.5 mm intervals in the 3–4 mm central segment of the relaxed fibre with a 40× dry objective (Zeiss, NA 0.60) and a 25× eyepiece. The fibre length (L₀) was adjusted to have a l_s of 2.4–2.5 μm, which is within the plateau region of the force–sarcomere length relation (Stephenson & Williams, 1982). The fibre cross-sectional area (CSA) was determined assuming the fibre cross-section as elliptical (CSA =π/4wh) and its value ranged between 3300 and 5100 μm². Fibres were activated by temperature jump using a solution exchange system (see Linari et al. 2007 and references therein). The fibre was transferred from the relaxing solution to pre-activating solution at 1°C and, after 2 min, to activating solution at 1°C. Force rose to a steady value that was 0.3–0.4 of the isometric force developed at the test temperature of 12°C. The fibre was then transferred to activating solution at the test temperature for 2–3 s for the mechanical test and then to relaxing solution at the same temperature. A striation follower (Huxley et al. 1981) allowed nanometre–microsecond resolution recording of length changes of a selected population of sarcomeres (500–1200) starting when an optic path was achieved via a glass window in the floor of the test temperature drop. The fibre length was controlled by the position of the lever of the loudspeaker motor (fixed-end mode) during the whole activation–relaxation period, except for ca 300 ms starting at the plateau of isometric force, when the mode was shifted from ‘fixed end’ to ‘force clamp’ (feedback signal from the force transducer).

Mechanical protocol

To record the isotonic velocity transient, stepwise drops to different fractions of the isometric force were imposed on the Ca²⁺-activated fibre in force-clamp mode. To account for the artifacts in the force transducer signal due to the change in both temperature and solution, 50 ms after the fibre was introduced into the test-temperature activating solution a large rapid shortening (6%L₀) was imposed on the fibre to induce slackness and record zero force in the test solution. Force redeveloped from the slack state and, once the isometric force had attained the plateau value (T₀), the control was shifted from fixed-end mode to force-clamp mode. Twenty milliseconds late, a step in force, completed within 150–200 μs, was imposed by using as a command signal the output of an integrated circuit that generated steps to preset fractions of T₀ (generally 0.75, 0.5 and 0.25 T₀). When the isotonic shortening had attained ∼60 nm hs⁻¹, the control was shifted back to fixed-end mode and the motor returned to its original position with a slow exponential time course. In force-clamp mode only the direct force signal was used in the feedback loop, while the velocity signal was taken from the motor lever position sensor. At any clamped force, several trials were necessary to adjust the gains of direct, velocity and lag amplifiers to optimise the force step. Measurements were done both in control and in the presence of 10 mm added P_i.

To elicit a stepwise drop in force within 200 μs requires higher gain with larger force steps, as the force after the step (and thus the fibre stiffness) is reduced. Consequently to set the feedback parameters for a satisfactory ramp-faced step without generating instability in the system became progressively more difficult. For this reason force drops below 0.25 T₀ were not applied. Alternatively, T–V relations both in control and in the presence of 10 mm P_i could be obtained by imposing different shortening velocities under loudspeaker motor control (fixed-end mode).

Force, motor position and sarcomere length signals were recorded with a multifunction I/O board (PCI-6110E, National Instruments) and a dedicated program written in LabVIEW (National Instruments) was used for signal recording and analysis.

Solutions

The composition of the solutions was as previously described in Caremani et al. (2008). The starting P_i concentration was adjusted by adding KH₂PO₄ and reducing the concentration of Na₂CP and EGTA/CaEGTA to achieve the same ionic strength (190 mm) as in the control solution (no added P_i). As already reported (Linari et al. 2007), the control solution without added P_i should contain about 1 mm P_i from two sources: P_i contamination in the experimental buffer and accumulation of P_i inside the fibre during contraction (Pate & Cooke, 1989a).

Results

The isotonic velocity transient

The isotonic shortening following a stepwise drop in force imposed on a demembranated fibre during isometric contraction at saturating Ca²⁺ in control conditions (no added P_i) exhibits the typical four phases (Fig. 1) already described for intact frog muscle fibres (Piazzesi et al. 2002).

The first phase consists in an abrupt reduction of half-sarcomere (hs) length which is simultaneous with the force step due to the undamped half-sarcomere elasticity. The estimate of the size of phase 1 shortening, L₁, is influenced by the rapid (phase 2) shortening which has the same direction and starts during the step itself. The effect of phase 2 is subtracted by back extrapolating, to the force step half-time (t_½), the tangent to the initial, almost linear part of phase 2 shortening (dashed line in Fig. 1A and B). L₁ increases with the size of the force step and the relation of L₁ versus the force attained at the end of the step (L₁ relation; black circles in Fig. 2E; means ± SEM bars from 5 fibres) can be interpolated with a linear regression equation that intercepts the ordinate at a value, 7.79 ± 0.11 nm hs⁻¹, representing the strain of the half-sarcomere at T₀ (193 ± 7 kPa in these fibres). The half-sarcomere compliance, C_hs, which is the slope of the relation, is 39.74 ± 2.42 nm MPa⁻¹, a value comparable with those previously determined using length steps at saturating Ca²⁺ (43.8 ± 2.1 nm MPa⁻¹: Caremani et al. 2008; 44.4 ± 5.5 nm MPa⁻¹: Linari et al. 2007).

Figure 2. Early phases of the isotonic velocity transient at different loads and the effect of P_i.

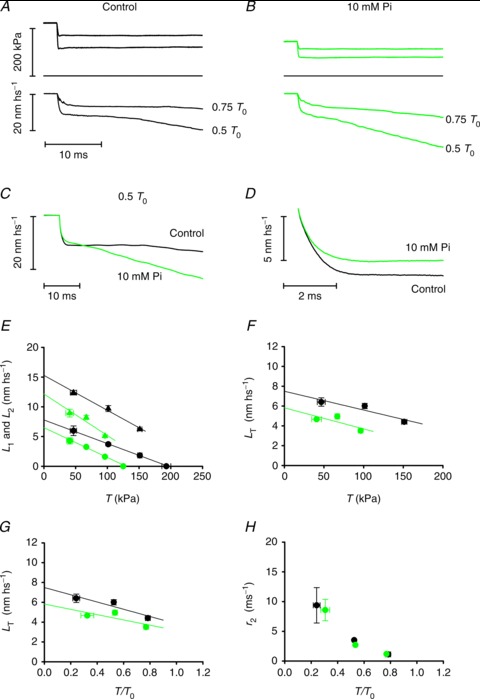
A and B, isotonic velocity transients (lower traces) following force steps (upper traces) to 0.75 and to 0.5 T₀ in the control (A) and in the presence of 10 mm P_i (B); middle traces, force baseline. C, superimposed isotonic velocity transients following a force step to 0.5 T₀ in control (black trace from A) and in 10 mm P_i (green trace from B). D, superimposed phase 2 transients in control (black trace) and in 10 mm P_i (green trace), obtained after subtracting phases 1 and 3 shortening as in Fig. 1C. E, relation of L₁ (circles) and L₂ (triangles) versus force in control (black symbols) and in 10 mm P_i (green symbols). F, relation between the shortening accounted for by the working stroke (L_T) and the force T (kPa) in control (black circles) and in 10 mm P_i (green circles). G, same relations as in F, with force expressed in relative units T/T₀. H, dependence of the rate constant of the working stroke (r₂) on force in control (black circles) and in 10 mm P_i (green circles). In panels E–H, data are the means ± SEM from the five fibres used in these experiments.

The rapid shortening (phase 2 of the isotonic velocity transient) following the elastic response is nearly exponential, as shown in Fig. 1C after subtracting the linear extrapolation of the trace in phase 3 from the shortening in phase 2 (dotted line in Fig. 1A). The amount of shortening attained at the end of phase 2, L₂, increases with the size of the force step (Fig. 2A). The L₂ relation (black triangles in Fig. 2E) can be fitted with a line that intercepts the ordinate at 15.28 ± 0.66 nm hs⁻¹ (Y₀; Ford et al. 1977; Piazzesi et al. 2002). Y₀ represents the maximum amount of shortening accounted for by both the strain of the half-sarcomere elastic elements (myofilaments and myosin motors) during the isometric contraction preceding the force step and the working stroke elicited in the motors by sudden unloading. The size of the shortening accounted for by phase 2 at each clamped force T relative to T₀, L_T, is obtained by subtracting the elastic response L₁ from L₂ (Fig. 1C) and represents the size of the myosin working stroke at that load. L_T increases with the reduction of the load (black circles Fig. 2F): L_T is just above 4 nm at 0.8T₀ and increases up to ∼6.5 nm at 0.25 T₀. The intercept on the ordinate of the linear fit to L_T data (the maximum working stroke at zero load) is ∼8 nm. The time course of the isotonic working stroke is nearly exponential (Fig. 1C) with a speed that increases with the reduction of the load (Fig. 2A). The rate constant of the process, r₂, is estimated by the reciprocal of the time (τ₂) from the end of the step to 63% of L_T. r₂ increases nearly exponentially with the reduction of the load (black circles in Fig. 2H) from ∼900 s⁻¹ at 0.8 T₀ to ∼9000 s⁻¹ at 0.25 T₀.

Phase 2 shortening is followed by a pause or a very slow shortening (phase 3, Fig. 1A), which eventually evolves to the final steady shortening at a velocity (about ten times slower than that of the initial part of phase 2, (Piazzesi et al. 2002) characteristic of the T–V relation (phase 4, black circles in Fig. 3B). Phase 3 is due to detachment of motors that almost synchronously have gone through the working stroke (Reconditi et al. 2004) and its end, marked by the downward inflection of the length trace, corresponds to the time when the motors begin the cyclical attachment–detachment regime. The end of phase 3 is measured as the time (t₃) from the beginning of the step to the intercept between the tangent to phase 4 shortening (dotted–dashed line in Fig. 1A) and the tangent to phase 3 (dotted line). The duration of phase 3 (τ₃), calculated by taking as the starting point the end of phase 2 (estimated as 2τ₂), decreases progressively with the reduction of the load (Fig. 2A), so that its reciprocal, r₃, an estimate of the rate of phase 3 motor detachment from actin following the synchronised execution of the working stroke, rises roughly exponentially with the reduction of the load (black circles in Fig. 3A) from ∼55 s⁻¹ (0.75 T₀) to ∼170 s⁻¹ (0.25 T₀). r₃ measured in this way is probably underestimated with respect to the value obtained directly from the rate of recovery of the X-ray interference signal (Fig. 2A and B in Reconditi et al. 2004), which is the reciprocal of the time to 63% of the recovery.

Figure 3. Late phases of the isotonic velocity transient at different loads.

A, dependence of the rate of phase 3 (r₃) on T/T₀ in control (black circles) and in 10 mm P_i (green circles). B, relations between force (T, kPa) and shortening velocity during phase 4 in control (black circles) and in 10 mm P_i (green circles). Lines are Hill hyperbolic equations fitted to the data (same colour code as for data). Inset, same relations (experimental data omitted) with force expressed as T/T₀. C, power–force relations calculated from data (symbols) and their fits (lines) in B. Inset, same relations with force expressed as T/T₀. Data are means ± SEM.

The effect of increased [P_i] on the velocity transient

The addition of 10 mm P_i to the bathing solution reduces the isometric force developed at saturating Ca²⁺ by ∼35% (Table 1), in agreement with previous work (Fortune et al. 1991; Kawai & Halvorson, 1991; Dantzig et al. 1992; Caremani et al. 2008). The isotonic velocity transient is elicited by imposing on the isometric contraction a stepwise reduction in force to the same relative loads as in the control (Fig. 2A and B). In 10 mm P_i (green traces) the transient maintains the same general shape as in the control (black traces), but exhibits an overall faster transition to phase 4.

Table 1.

Relevant parameters (means ± SEM) of the isometric contraction

	T0 (kPa)	Y0 (nm)	Chs (nm MPa−1)
Control	193 ± 7	7.79 ± 0.11	39.74 ± 2.42
10 mm Pi	125 ± 6	6.67 ± 0.09	51.65 ± 3.10

Data from five fibres.

The L₁ relation (green circles in Fig. 2E) shows a smaller reduction of the ordinate intercept (∼15%) than that of the abscissa intercept (∼35%), so that C_hs in 10 mm P_i becomes 51.65 ± 3.10 nm MPa⁻¹, ∼27% larger than in control, in agreement with previous findings using length steps (Caremani et al. 2008), which shows that addition of P_i reduces the hs strain less than the isometric force because the strain of the myosin motors remains constant while their number reduces in proportion to the isometric force.

In 10 mm P_i the rapid phase 2 shortening appears truncated by a steeper and quicker phase 3, as shown in Fig. 2C by superimposing the transients at 0.5 T₀ in control (black line) and in the presence of 10 mm P_i (green line). L₂, calculated as shown in Fig. 1 (green triangles in Fig. 2E), is reduced at any force, and its ordinate intercept (12.75 ± 0.67 nm hs⁻¹) is smaller than in the control. Since [P_i] reduces the isometric force solely by reducing the number of force-generating motors (Caremani et al. 2008), the isotonic working stroke (L_T) can be related to the actual load on each individual motor by plotting L_T versus the force T relative to the isometric force T₀ in either condition (Fig. 2G; control, black circles; 10 mm P_i, green circles). Also, at the same load per motor the working stroke in 10 mm P_i is smaller than in the control. The reduction is larger at low load, and the linear fit to data gives an estimate of the zero load working stroke (the ordinate intercept) of ∼6 nm (∼75% the control value). On the other hand, the speed of the working stroke at the same relative load is not affected by the increase in P_i, as shown by the superimposed phase 2 responses in Fig. 2D (control, black line; 10 mm P_i: green line). r₂ at any load in 10 mm P_i is almost the same as in the control (Fig. 2H), increasing roughly exponentially with the reduction of the load.

It is also evident from direct inspection of the traces in Fig. 2A (control) and B (10 mm P_i) that the increase in [P_i] reduces the duration of phase 3 and increases the velocity of phase 4 for the same relative load. These effects are emphasised in Fig. 2C by superimposing the velocity transients in the control (black line) and in 10 mm P_i (green line) for a step to 0.5 T₀ τ₃ at any relative load is shorter than in the control, so that the r₃–T/T₀ relation in 10 mm P_i (green circles in Fig. 3A) is shifted upwards with respect to the control (black circles), maintaining the exponential shape. At 0.5 T₀ r₃ is ∼70 s⁻¹ in the control and doubles in 10 mm P_i.

The reduction by P_i of the steady shortening velocity in phase 4 (V) is much less than the reduction of the isometric force (compare green circles (10 mm P_i) and black circles (control) in Fig. 3B). Consequently, at the same relative load, V is larger in 10 mm P_i than in the control and the curvature of the relation is reduced (inset in Fig. 3B). The lines in Fig. 3B are the fits to the force–velocity data (black, control; green, 10 mm P_i) of the Hill hyperbolic equation (Hill, 1938):

(1)

where a and b are the distances between the asymptotes and the ordinate and abscissa axes (related to the curvature of the force–velocity relation) and V₀ (the ordinate intercept) estimates the maximum velocity of shortening or the unloaded shortening velocity. As shown also by Hill parameters (Table 2), the addition of 10 mm P_i increases the shortening velocity at any relative load, without significant effect on V₀, which implies a reduction in the curvature of the T–V relation.

Table 2.

Relevant parameters (means ± SEM) of the force–velocity relation in the control and in 10 mm P_i

	a/T0	b (nm s−1 hs−1)	V0 (nm s−1 hs−1)
Control	0.108 ± 0.014	368 ± 89	4133 ± 103
10 mm Pi	0.214 ± 0.085	795 ± 478	4262 ± 265

Force in units relative to T₀ in the respective solution; a, b and V₀ defined in the text.

T–V relations are used to calculate the power output (T×V) as a function of the load in Fig. 3C. A rise in P_i reduces the power only at high loads (above 50 kPa, green line), so that, when plotted versus the same relative load (inset in Fig. 3C), in 10 mm P_i the maximum power output (occurring at ∼0.3 T₀) increased by 80%.

The kinetic model

The isotonic velocity transient and its modulation by P_i provide quite stringent constraints for a mechanical–kinetic model of the in situ action of the myosin II motors (Piazzesi et al. 2002, 2007; Reconditi et al. 2004; Decostre et al. 2005). As a starting point in the simulation we used a model (see Fig. 4A, black transitions) that integrates a kinetic model capable of simulating the P_i dependence of isometric force and ATPase rate (scheme 2 in Linari et al. 2010) with the Huxley–Simmons model of the working stroke (Huxley & Simmons, 1971). Binding of an ATP molecule to the catalytic site of the myosin head induces dissociation of the myosin motor, M, from actin (step 1), which is followed by the recovery of the conformation of the motor at the beginning of the working stroke and the hydrolysis step (step 2). The M.ADP.P_i–AM.ADP.P_i state represents both the detached (M.ADP.P_i) and the weakly actin-bound (AM.ADP.P_i) motors with the hydrolysis products still bound to the catalytic site. Strong binding of M to an actin monomer A (step 3), caused by the closure of the actin binding cleft (Geeves & Holmes, 2005), implies the formation of the first of four different force-generating states, AM₁.ADP.P_i, that, without significant delay, undergoes the interdomain structural transition leading to the strained conformation responsible for the isometric force (Huxley & Simmons, 1971). The structural transition can occur in any of the biochemical states AM.ADP.P_i, AM.ADP and AM (but in practice when the motor works under physiological conditions only in the first two) and implies three subsequent structural transitions or force-generating steps (M₁→M₂, M₂→M₃ and M₃→M₄) controlled by strain-dependent rate constants. For simplicity, in the absence of specific constraints related to the effect of [ADP], the rate constants of the three transitions are assumed to have the same strain dependence for either state AM.ADP.P_i or AM.ADP, while the values of the rate constants for the AM state (rigor) are 100 times lower. According to the principle of the nearest-neighbour interaction, attachment to the actin monomer (A, approximately 5.5 nm in diameter) occurs for a range of x from –2.75 nm to 2.75 nm, where x is the relative axial position between the motor and A, and is zero for the position of the centre of distribution of attachments of the motors in the M₁ state. The number of force-generating steps is set to three to fit the transition and equilibrium kinetics of the working stroke under the following two conditions. (i) The stiffness of the myosin motor sets a limit to the size of the force-generating step (z) with regard to the ability to reproduce the rate and amplitude of phase 2 of the transient following perturbation in length and load (Piazzesi & Lombardi, 1995; Piazzesi et al. 2002; Woledge et al. 2009; Park-Holohan et al. 2012); the motor stiffness in this work is 1.2 pN nm⁻¹, but with the recovery of lattice dimension in the skinned fibre the stiffness rises to 1.7 pN nm⁻¹. Under these conditions the force and length transients are satisfactorily fitted with z= 3.1 nm. (ii) The maximum sliding distance accounted for by the working stroke in the attached motor, measured either by the maximum step release for which force is recovered in phase 2 (abscissa intercept of the T₂ curve of Huxley & Simmons, 1971; Piazzesi & Lombardi, 1995) or by the extent of rapid shortening following a force step to zero (Piazzesi et al. 2002; Reconditi et al. 2004), is ∼10 nm.

Figure 4. Chemo-mechanical cycle of the myosin motor and free energy diagrams of the four structural states of the actin-attached myosin motor in the AM.ADP.P_i state.

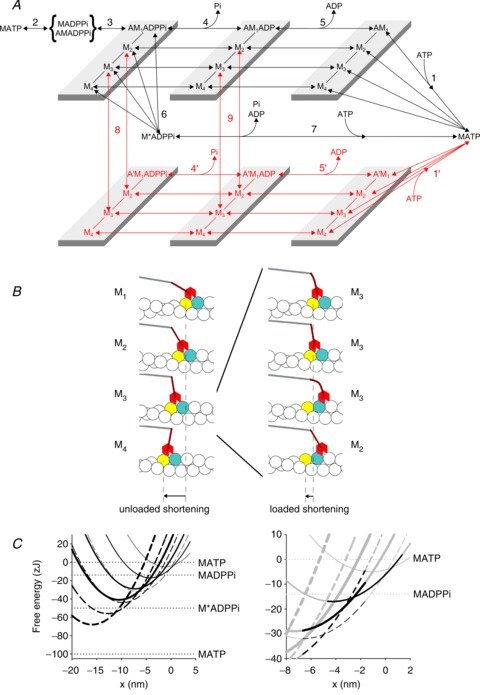
A, scheme representing the chemo-mechanical cycle assumed in the model simulation. The black transitions indicate the cycle undergone by myosin motors that interact with only one actin monomer (A). The red transitions indicate the cycle undergone by myosin motors that slip to the next actin monomer 5.5 nm away from the centre of the sarcomere (A′). M₁–M₄ represent the structural states for a given biochemical state of the attached myosin motor (AM.ADP.P_i, AM.ADP or AM). B, left panel: pictorial representation of the model showing the four structural states under unloaded conditions. B, right panel: representation of the slip of the M₃ state from A to the next actin monomer (A′) during loaded shortening, followed by strain-dependent state re-equilibration. Colour code for the interacting actin monomers: A, yellow, A′, blue. Colour code for the myosin molecule: catalytic domain, red, lever arm, brown, S2 portion connected to the backbone, grey. C, left panel: free energy diagrams of the four structural states of the myosin motor in the AM.ADP.P_i state, attached to either the original actin monomer (A, continuous lines) or the next actin monomer farther from the centre of the sarcomere (A′, dashed lines). The thickness of the line identifies the progression of the state transitions, from M₁, thinnest line, to M₄, thickest line. The slip from A to A′ corresponds to a leftward 5.5 nm shift and a downward 27 zJ shift of the minimum of the free energy parabola of the motor in each state; the increase in strain of the motor implied in the A–A′ transition is shown by the difference in slope of the two free energy parabolas at the same x. x is zero in correspondence of the free energy minimum of a myosin motor attached to A in the M₁ state. Horizontal lines show the free energy of the detached states. C, right panel: shown in grey are the same diagrams as in the left panel, but on an expanded scale to show the energy profiles in the x range concerning the slipping transition. Shown in black are the free energy profiles of the states populated during steady shortening at a velocity (<1000 nm s⁻¹) that maximises the slipping process. The A-attached M₂ motor (thinner continuous line) dwells between the transition to the M₃ state (thicker continuous line) or the slipping to A′(dashed line with the same thickness); the increase in strain following the slipping favours the backward state transition to M₁ (thinnest dashed line).

Both the biochemical events in the attached motor, release of P_i (step 4) and release of ADP (step 5), can occur in any of the four states, the rate constants of P_i release and ADP release increasing with the progression of the motor through the working stroke from M₁ to M₄. This means that the biochemical steps are conformation dependent.

In terms of the crystallographic model (Geeves & Holmes, 2005) the M₁–M₄ states correspond to conformations of the motor with progressive swinging of the lever arm, as shown in the diagram of the structural states under unloaded conditions in the left panel of Fig. 4B. ADP release, but not P_i release, is also strain dependent, that is, for the same conformation its rate constant depends on x. At the same x, the strain depends on the conformation, increasing by 3.1 nm for each state transition M₁–M₂, M₂–M₃, or M₃–M₄. Therefore at any position x the total strain on the motor in the state M_i is given by y_i= (zi+x+x₀), where i is 0, 1, 2, 3 for the states M₁, M₂, M₃, M₄, respectively, and x₀ is the strain of the M₁ state at x= 0, which has been set to 1.15 nm.

The scheme retains the possibility of an unconventional detachment of the myosin motor from actin at an early stage of the ATPase cycle (Linari et al. 2010), with the hydrolysis products still bound to the catalytic site (step 6), followed by fast release of products and binding of a new ATP (step 7).

Isometric contraction

The development of isometric force is rate limited by both the ATP hydrolysis step (step 2; Bagshaw & Trentham, 1974; White & Taylor, 1976; Sleep et al. 2005) and the attachment of cross-bridges (step 3), which then undergo the force-generating transition without significant further delay (Huxley & Simmons, 1971; Linari et al. 2010). Effectively only the M₁ and M₂ states of the motor are responsible for the isometric force, as the subsequent steps in the series of M₁–M₄ transitions are progressively prevented by the increase of the mechanical energy (Huxley & Simmons, 1971; Piazzesi & Lombardi, 1995; Decostre et al. 2005). In structural terms this means that the changes leading to tilting of the lever arm progress only partway. The flux through the biochemical steps is limited by the fact that ADP can be released only following opening of the nucleotide binding pocket (Geeves & Holmes, 2005); thus in isometric conditions ADP release becomes the rate limiting step (Nyitrai & Geeves, 2004; Sleep et al. 2005; West et al. 2005) and motors are predominantly in AM.ADP.P_i and AM.ADP states (see Supplemental Fig. S2). The flux through the unconventional path (Linari et al. 2010) occurs solely from the AM.ADP.P_i state and involves ∼1/4 of the cycling motors, while the remaining flux involves M₂ and M₃ motors completing the biochemical steps while attached (ordinate intercept of Supplemental Fig. S3).

Isotonic velocity transient

The step reduction in load below the isometric force removes the mechanical energy barrier and favours the synchronous structural transition to states M₃ and M₄, as shown by the early rapid shortening (phase 2 of the isotonic velocity transient). The biochemical steps promoted by the corresponding movement of the lever arm and opening of the nucleotide binding pocket are the release of ADP (step 5), the binding of a new ATP and the dissociation of the myosin head from actin (step 1). The synchronisation of these biochemical events leads to a transient loss of the ability of motors to power further shortening (phase 3 of the isotonic velocity transient), as the motors that were responsible for the initial isometric force can interact again with an actin monomer further along the thin filament only after the ATP hydrolysis step (step 2), the rate constant of which in the experimental conditions used here (12°C) is set to 30 s⁻¹ by solution kinetics and fibre measurements (Bagshaw & Trentham, 1974; White & Taylor, 1976; Sleep et al. 2005). Thus the time taken by these motors to enter into the steady state cycling rate should mark the end of phase 3.

The model considered so far (black transitions in Fig. 4A) was unable to fit this stage of the isotonic transient, because the observed rate of isometric force development sets a limit to the rate at which motors detaching at the end of phase 2 of the isotonic velocity transient are substituted by new motors responsible for the transition to steady shortening velocity. This rate is measured by r₃ (black circles in Fig. 3A). Both processes, the rate of isometric force development and r₃, are thought to be kinetically controlled by steps 2 and 3. With the rate constant of step 2 set to 30 s⁻¹, the only adjustable parameter is the rate of step 3. Once this rate is set to a value adequately low to fit the rate of isometric force development (dashed line in Fig. 5A), it results too low to predict the time courses of the termination of the pause and the start of steady shortening. In fact, following the synchronous execution of the working stroke elicited by the force step, the imposed load becomes transiently too large for the motors to provide shortening, leading to a pause longer than is observed (dashed line in Fig. 5B) or, for loads >0.7 T₀, to transient lengthening and exaggerated oscillatory behaviour.

Figure 5. Comparison between experimental data (black) and the responses of the model (blue).

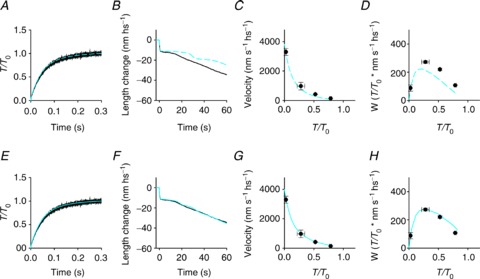
Upper row, blue dashed lines: model not including the possibility of the myosin motor slipping to the second actin monomer. Lower row, blue continuous lines: model including the possibility of slipping to the second actin monomer. A and E, isometric force development. B and F, isotonic velocity transient following a step to 0.5 T₀. C and G, force–velocity relation. D and H, power–force relation. Black trace in B and F from Fig. 2A; symbols in C and G from black symbols in Fig. 3B; symbols in D and H from black symbols in Fig. 3C.

In order to simulate the steady state force–velocity relation, this problem of transient instability can be circumvented by changing the model algorithm from isotonic to isovelocity conditions. In this way it can be seen that the kinetic limit intrinsic to the black transitions in Fig. 4A shows up as a lower-than-observed force at any velocity, which means an increased curvature of the force–velocity relation (Fig. 5C) and a reduced power (Fig. 5D).

Motor interaction with two consecutive actin monomers

We postulate that the mechanism that fits the duration of phase 3 of the isotonic velocity transient and the steady state force– and power–velocity relations, without affecting the rate of the isometric force development (Fig. 5E–H), is based on the possibility that a myosin motor can slip between two consecutive actin monomers while it is still at an intermediate stage of its biochemical and structural cycle. The interaction of a myosin motor with several adjacent actin monomers on the same strand during an ATPase cycle has been originally proposed by Yanagida and co-workers to explain the stepwise movement of myosin in single molecule experiments with scanning probe microscopy (Kitamura et al. 1999). We propose that, for critical values of x in the shortening direction, the M₂ and M₃ motors, with both ligands or ADP in their catalytic site, can slip from the actin monomer to which they were originally attached to the next actin monomer, 5.5 nm further from the centre of the sarcomere (A′, red transitions in Fig. 4A, steps 8 and 9). This allows these motors to recover 5.5 nm strain while remaining in the same structural state and then undergo rapid state re-equilibration according to the strain-dependent rate functions followed by the completion of the structural and biochemical cycle (steps 4′, 5′ and 1′). The slip during shortening from the actin monomer A (yellow) to A′ (blue) of an M₃ motor in the AM.ADP state is detailed in the right panel of Fig. 4B. The slipping transition implies an increase of 5.5 nm in the motor strain, as shown by the 5.5 nm shift of the free energy parabola of the A′-attached motor (dashed lines in Fig. 4C, where the thickness of the line increases progressing from M₁ to M₄), with respect to the corresponding parabola of the A-attached motor (continuous lines, thickness code as for dashed lines). The slipping process is assumed to occur with the motor in the same structural state, and the corresponding increase in the mechanical energy is accounted for by a downward shift of the minimum of the free energy parabola of the A′-attached motor by 27 zJ, with respect to the corresponding parabola of the A-attached motor, so that the process occurs near equilibrium in a narrow range of x. In the right panel of Fig. 4C the free energy profiles of the states concerned in the relevant transitions undergone by an M₂ motor in the AM.ADP.P_i state during steady shortening are delineated in black with respect to the grey profiles that complete the scenario shown in the left panel. It can be seen that at ∼–2.5 nm the A-attached M₂ motor (thinner continuous line) can either undergo the state transition to M₃ (thicker continuous line) or slip to A′ (dashed line with the same thickness), in which case the 5.5 nm increase in strain favours the backward state transition to M₁ (thinnest dashed line).

As detailed in the Supplemental Material, the overall free energy change accounting for the M₁–M₄ transitions while the motor is attached to the same actin in the same biochemical state is 36 zJ and the free energy changes associated with the biochemical steps (see Supplemental Fig. S1) are 15.4 zJ for P_i release (in control conditions, no added P_i) and 5.1 zJ for ADP release. Thus, at difference with the original idea by Yanagida and co-workers (Kitamura et al. 1999), only one slipping transition implying 27 zJ of free energy change is energetically compatible with the free energy made available by ATP hydrolysis.

Following the synchronous execution of the working stroke during phase 2 of the isotonic transient, the slip occurs from both M₂ and M₃ motors, while during steady shortening, the slip mainly occurs from M₃ motors, as the strain-dependent increase in the rate constant of state transitions favours a distribution of the motors ahead in the working stroke. The simulation is optimised by tuning the x dependency of the rate constants of steps 8 and 9 (Fig. 4A) controlling the flux of motors slipping to A′ in relation to their biochemical (either AM.ADP.P_i or AM.ADP) and structural (either M₂ or M₃) state. This flux is maximal during shortening at high loads (T > 0.4 T₀; V < 1000 nm s⁻¹ hs⁻¹); when, as shown in Supplemental Fig. S3, ∼0.4 of cycling motors shifts on A′, while ∼0.4 completes its working stroke on A and ∼0.2 undergoes the detachment from actin at an early stage of the ATPase cycle. For lower loads (and higher shortening velocities) the myosin slip to A′ is progressively prevented by the increase of the strain-dependent rate constants of the state transition on the first actin, which favours the completion of the working stroke and, via formation of M₄ motors, the rapid termination of the conventional biochemical cycle (steps 5 and 1). In this respect it must be noted that another requirement is that the rate constant of ADP release increases not only with the structural transition leading to M₄ (that is, in terms of the crystallographic model, with the progressive swinging of the lever arm and opening of the nucleotide binding pocket), but also with the degree of negative strain on the motor (see Supplemental Table S1). During shortening under zero load the dominating path for the motor to terminate its ATPase cycle is through the conventional cycle (2/3 of the total ATPase rate, Supplemental Fig. S3).

Effect of increased [P_i]

The rise in [P_i] reduces the free energy level of the AM.ADP and AM states (see Supplemental Fig. S1) and thus increases the second order rate constant of the reversal of step 4 (k₋₄). This causes the shift in the equilibrium of attached motors towards the AM.ADP.P_i state and explains the reduction of the number of motors and isometric force and the increase in the rate of force development (Dantzig et al. 1992; Linari et al. 2010).

Both the amplitude of phase 2 and the duration of phase 3 of the isotonic velocity transient following the force step are reduced by the rise in [P_i] (Fig. 2C–G). Truncation of phase 2 and the increase of r₃ induced by P_i (Fig. 3A) are reproduced by the model (compare black and green lines in Fig. 6A) because in the preceding isometric contraction the rise in the proportion of M motors in the AM.ADP.P_i state increases with respect to those in the AM.ADP state and this enhances the probability of detachment from actin through step 6 at any stage of the working stroke, followed by a rapid termination of the ATPase cycle (step 7). In spite of the truncation of phase 2 of the velocity transient, the rate of phase 2 state transitions at the same relative load is not affected by the increase in [P_i] (green and black circles in Figs 2H and 6B). This finding sets a fundamental constraint that is accounted for by the assumption that the biochemical steps are orthogonal to the working-stroke steps (green and black triangles in Fig. 6B).

Figure 6. Comparison of the results of the simulation in control (black) and in the presence of 10 mm P_i (green).

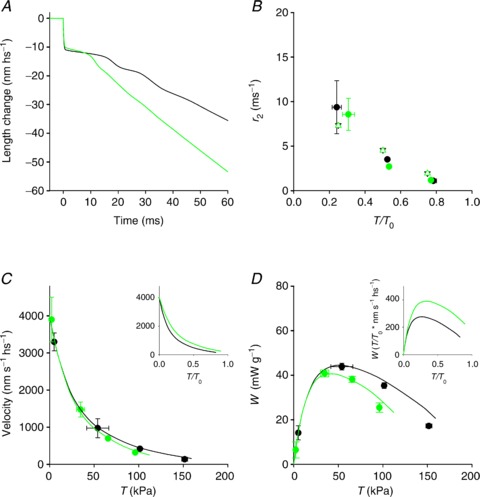
A, simulated isotonic velocity transient following a step in force to 0.5 T₀. B, dependence of r₂ on T/T₀ (filled circles, data from Fig. 2H; open triangles, simulation). C, force–velocity relations (circles, data from Fig. 3B; lines, simulation). D, power–force relation (circles, from Fig. 3C; lines, simulation). Inset in C and D simulated relations in relative units.

During steady shortening, with the reduction of the load, the motor distribution is shifted towards the end of the working stroke and the conformation-dependent increase in the rate of P_i release promotes the flux through step 4, at the expenses of the flux through step 6, just as occurs in control conditions. Similarly the strain-dependent increase in detachment rate via steps 5 and 1 ensures that the shortening velocity under low load is the same, independent of P_i.

Thus the inhibitory effect of P_i is maximal at high load and progressively reduces at lower loads (Fig. 6C: circles, data; lines, model simulations). Consequently, when the force–velocity relation is set relative to the isometric force, the 10 mm P_i points lie above those in control, the curvature of the relation is reduced (inset in Figs 3B and 6C) and the corresponding maximum power is increased (inset in Figs 3C and 6D).

Discussion

The isotonic velocity transient defines the kinetics and the size of the myosin working stroke and its regeneration

The isotonic velocity transient following a stepwise drop in force is a very powerful tool to define how the extent and rate of the working stroke of the myosin motors and its regeneration depend on the load. The model simulation indicates that the velocity transient is the expression of the combination of several kinetic processes: the strain-dependent structural transitions M₁–M₄, the conformation-dependent orthogonal biochemical steps of P_i release (step 4) and ADP release (step 5) and a third process orthogonal to both that allows the motor at an intermediate stage of the working stroke either to detach with both ligands on its catalytic site and rapidly complete the biochemical steps, or to slip, with both ligands or only ADP in its catalytic site, on the next actin monomer farther from the centre of the sarcomere, and complete the structural and biochemical steps.

Slipping of a motor on the next actin monomer (A′), while the actin filament slides for the collective action of the other motors, produces 5.5 nm increase of its strain while being in the same structural state (Fig. 4B and C), followed by state re-equilibration towards the beginning of the working stroke. This provides the supplementary work capability that accounts for the observed smooth and relatively rapid phase 3 transition to steady shortening. In the absence of this mechanism, the synchronised termination of the working stroke elicited in the attached motors by the force step would be followed by a transient deficit of the force generation capability of the motors that would prolong phase 3 and, at high load, would generate instability (Fig. 5B).

The working stroke and the release of P_i are orthogonal processes

The increase in [P_i] does not affect the rate of phase 2 following a stepwise drop in force, demonstrating that the state transitions responsible for the working stroke, namely the conformational changes in the converter leading to the tilting of the lever arm and opening of the nucleotide binding pocket, are independent of the presence of P_i in the catalytic site. However, the rate of P_i release depends on the state of the motor, which means that it is conformation dependent and occurs at a higher rate with the working stroke progression (see Supplemental Table S1). This view is also supported by an earlier finding that the rate of force drop following a step increase in [P_i] (Homsher et al. 1997) is larger if the step is imposed during shortening than during isometric contraction. Moreover, the increase in the rate of P_i release with the progression of the working stroke explains why lowering the load counteracts the inhibitory effect of an increase in [P_i] on the force–velocity relation and power. The other process orthogonal to both the working stroke and P_i release is the early detachment from the AM.ADP.P_i state (step 6). The truncation of phase 2 by a rise in [P_i] is reproduced by the model (Fig. 6A) if the early detachment occurs not only during isometric contraction (Linari et al. 2010) but also from states further ahead in the working stroke.

The demonstration in this work that P_i release is independent of the working stroke, and in turn that the working stroke can occur with or without P_i in the catalytic site of the motor, provides a straightforward explanation of the finding that during shortening the rate of the force drop following a step in P_i depends on the final [P_i] in the same way as during isometric contraction (Homsher et al. 1997). Conventional models that assume that P_i release is tightly coupled to the working stroke use only two parabolas to represent the energetic scenario, the first parabola for the AM.ADP.P_i state at the beginning of the stroke and the second for the AM.ADP state at the end of the stroke. In this way, lowering the load (or increasing the shortening speed) biases both the motor conformation towards the end of the stroke and the biochemical transition to AM.ADP motors that are insensitive to [P_i] because, at the same x, are energetically too far from the equilibrium with the AM.ADP.P_i motors.

This energetic barrier is removed by uncoupling the biochemical and the conformational transitions.

Our conclusion that the P_i release occurs independently of the motor conformation presesnts a new scenario about the structural dynamics of the working stroke itself, which could be made by smoother transitions between many more conformations.

Mechanics and energetics of shortening muscle are explained by the ability of the myosin motor to use two consecutive actin monomers

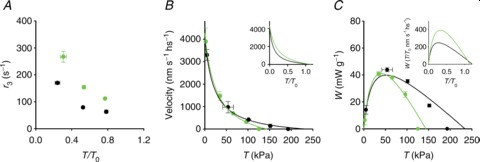
The model simulation indicates that in order to fit observed force– and power–velocity relations (Fig. 5G and H) it must be possibile for the actin-attached motors engaged in the working stroke to slip to the next actin monomer farther from the centre of the sarcomere (A′), while the actin filament is sliding along for the collective action of the other attached motors. The attachment to A′ implies 5.5 nm recovery of the strain and then state re-equilibration according to the strain-dependent rate constants of the M₁–M₄ transitions (right panel in Fig. 4B). Release of ADP by the motor attached to A′ in any of the M₁–M₄ states and subsequent binding of ATP and detachment are governed by the same conformation- and strain-dependent kinetics as those of motors attached to the first actin (A). Therefore the motors that detach from the second actin (A′) have undergone the same working stroke as those that complete their cycle and detach from the first actin (A).

On the other hand, the sliding distance per ATPase cycle accounted for by the motors that slip to A′ is 5.5 nm larger than that of motors that complete their cycle on A. Consequently the average sliding distance for a myosin working cycle (L_w) during steady shortening at any given load is the weighted mean of the sliding distances with and without the slip to the second actin. L_w is significantly larger than the average motor working stroke (d), calculated as the weighted mean of the axial movement accounted for by the tilting of the lever arm in the attached motors during steady shortening at the same load (Fig. 7A; blue line, L_w; red line, d). In the range of loads between 0.8 T₀ and 0.3 T₀ (V < 1000 nm s⁻¹ hs⁻¹), L_w is 6–7 nm while d is 3–4 nm. The proportion of interacting motors undergoing the slip to A′ is maximal in the same range of loads (Supplemental Fig. S3).

Figure 7. Simulation of mechanical and energetic parameters of the shortening muscle.

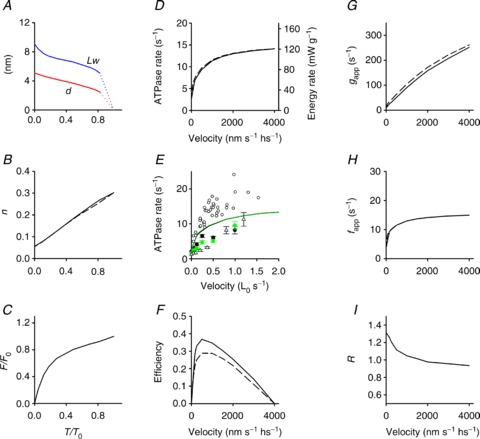
A, dependence on T/T₀ of the average motor working stroke (d, red line) and of the average sliding distance during a motor working cycle (L_W, blue line). B, fraction of attached motors versus T/T₀. C, force per myosin motor relative to the isometric value (F/F₀) versus T/T₀. D, dependence on shortening velocity of the rate of ATP hydrolysis per myosin head (left ordinate, s⁻¹) and of the rate of energy liberation calculated as detailed in the text (right ordinate, mW g⁻¹). E, symbols: observed ATPase rate in control (black symbols) and in 10 mm P_i (green symbols) versus shortening velocity (open circles, He et al. 1999; filled circles, Potma & Stienen, 1996; open triangles, Sun et al. 2001). E, lines: model simulation in control (black) and in 10 mm P_i (green). F, efficiency versus shortening velocity. G and H, g_app and f_app versus shortening velocity. I, dependence on shortening velocity of the ratio (R) of the ATPase rate per myosin motor in 10 mm P_i over the control. Where present, the dashed lines are the simulations using the model that does not include the possibility of the motors slipping to the second actin.

The number of actin-attached motors during steady shortening decreases almost in proportion to the load (Fig. 7B), so that at high loads the force per attached motor (F) reduces only slightly with respect to the isometric value (F₀): in the range of loads 0.8–0.3 T₀, F maintains a value >0.7 F₀ (Fig. 7C). The conclusion of the model simulation that, during steady shortening at high and intermediate loads, each myosin motor accounts for a sliding distance of 6–7 nm maintaining a force similar to the isometric value fits the requirements for maximization of power and efficiency of skeletal muscle (Piazzesi et al. 2007).

The rate of ATP hydrolysis per myosin head (k_CAT) during steady shortening at any given load, calculated from the flux through the hydrolysis step (step 2) is reported in Fig. 7D (black continuous line, left ordinate, s⁻¹). The ATPase rate is 2.7 s⁻¹ per myosin head in isometric contraction and increases up to 11 s⁻¹ with the reduction of the load to the value for the maximum power (T≥ 0.3 T₀, V≤ 1000 nm s⁻¹). Further reduction in the load (increase in shortening velocity) up to zero produces only a minor increase in ATPase rate up to ∼14 s⁻¹. This behaviour fits with the rate of energy liberation measured by combining power and rate of heat production in intact fast muscle (Hill, 1938; Woledge et al. 1985; Linari & Woledge, 1995). Accordingly, the rate of ATP hydrolysis measured in skinned fibres by fluorescence of either phosphate binding protein (He et al. 1999) or NADH (Potma & Stienen, 1996; Sun et al. 2001) exhibits the same dependence on shortening velocity, within the limited range of velocities explored (black symbols in Fig. 7E).

The ATPase rate–V relation obtained with the model simulation that does not include the possibility of working motors slipping to the second actin (scheme limited to transitions denoted in black in Fig. 4A) is shown by the black dashed line in Fig. 7D, to emphasize that the ability of the motors to slip to the next actin (scheme including the transitions denoted in red in Fig. 4A) does not imply per se any significant change in the rate of ATP hydrolysis, but only an increased efficiency in the utilization of ATP free energy. This is due to the fact that the proportion of the energy change of the ATP hydrolysis associated with the path along the free energy parabola of the actomyosin motor is larger when the motor slips to the second actin. In fact, as shown in Fig. 4C, the level of the free energy minimum of the motor is shifted downward by 27 zJ if it is attached to A′ with respect to A.

The relation between efficiency and shortening velocity predicted by the model is shown by the continuous line in Fig. 7F. The relation is obtained from the ratio between the power (from the relation in Fig. 5H) and the rate of energy liberation (black line in Fig. 7D, right ordinate, mW g⁻¹), calculated from the ATPase rate assuming a concentration of myosin heads in the psoas skinned fibre of 0.15 mm (He et al. 1997; Tikunov et al. 2001) and a free energy of 60 kJ mol⁻¹ (Barclay et al. 2010). The maximum efficiency is shifted towards higher loads (≥0.5 T₀, V≤500 nm s⁻¹) with respect to the maximum of the power–velocity relation and is ∼0.37, in accordance with data in the literature (Barclay et al. 2010 and references therein). In contrast, the maximum efficiency predicted by the model that does not include the possibility of motors slipping to the second actin (black dashed line in Fig. 7F, obtained from the ratio between the power (blue dashed line in Fig. 5D) and the rate of energy liberation (black dashed line in Fig. 7D)) is too low (∼0.28).

In terms of the simplified two-state model of A. F. Huxley (Huxley, 1957) the rate at which ATP is hydrolysed per myosin head (k_CAT) is related to the apparent rate constant for motor attachment, f_app, and detachment, g_app, by the equation:

(2)

where n is the fraction of attached heads. In isometric contraction, n∼0.3 and k_CAT∼2.7 s⁻¹ per myosin head (Linari et al. 2007, 2010, and references therein), so that g_app= 9 s⁻¹ and f_app= 3.9 s⁻¹. During shortening, k_CAT increases with the shortening velocity V and from the relations k_CAT–V (black continuous line in Fig. 7D) and n–V (calculated from Fig. 7B) the dependences of g_app and f_app on V are calculated and reported as continuous lines in Fig. 7G and H, respectively. In agreement with previous conclusions (Piazzesi et al. 2007), g_app increases almost linearly with the velocity, attaining a maximum value of ∼250 s⁻¹ at V₀, while f_app increases sharply at low velocity and then progressively less and at V₀ attains a maximum value about 3 times larger than that in isometric contraction. Dashed lines in Fig. 7B, D, G and H refer to the same parameters as the continuous lines but calculated using the model that does not include the possibility of the myosin motor slipping to the second actin. It is evident that, as for the ATPase rate and the fraction of attached motors, also for g_app and f_app the dependence on velocity is not substantially affected by the assumption that the myosin motor can complete its working stroke using a second actin.

The model with two actin interactions is also able to explain the mechanical and structural evidence that the working stroke elicited by a step release is regenerated at a rate (∼100 s⁻¹) much faster than expected from the ATPase rate (Irving et al. 1992; Lombardi et al. 1992; Chen & Brenner, 1993). In this connection, it must be noted that alternative models capable of accounting for the rapid regeneration of the myosin working stroke and maximum power during steady shortening have been proposed, based on mechanisms that imply faster recruitment of new motors during shortening. Some of these models assume that during shortening the partner head of the same myosin molecule can attach much faster, due to the conformation assumed by the first head during its working stroke (Huxley & Tideswell, 1997; Mansson, 2010). Other models assume intermolecular cooperativity (Duke, 1999; Tanner et al. 2007; Smith et al. 2008; Smith & Mijailovich, 2008). However, none of them can predict the integrated mechanics and energetics of shortening muscle, because the underlying mechanisms would imply recruitment of new motors and thus a correspondingly higher rate of ATP hydrolysis, and would fail to match the high efficiency achieved by the slippage mechanism (Fig. 7F), which allows, for each ATP driven working cycle, an average sliding distance L_w larger than the average working stroke d (Fig. 7A).

Structural hint for the hypothesis that myosin II in muscle can use two actin monomers during its working stroke is provided by the crystallographic model of the actin–myosin complex, which suggests that a weak interaction is present between the lower edge of the myosin pocket forming the strong bond with an actin monomer, and the neighbouring actin monomer in the direction farther from the centre of the sarcomere (Holmes et al. 2004).

P_i effect on the mechanics and energetics of shortening muscle

The addition of 10 mm P_i reduces the isometric force by reducing the number of interacting motors by 35–40%, while the ATPase rate is reduced only by 15% (Bowater & Sleep, 1988; Potma et al. 1995; Potma & Stienen, 1996; Caremani et al. 2008; Linari et al. 2010). Consequently the ATPase rate per interacting motor is increased by 40%. This is reproduced by the model that allows P_i promotion of early detachment of the force-generating motors followed by product release and attachment of a new ATP (Linari et al. 2010).

In the shortening muscle, the effect of increased [P_i] on both ATPase (Potma & Stienen, 1996; see Fig. 7E, filled black and green circles), and force (Fig. 3B) is reduced with respect to the isometric contraction, so that the relations of these two parameters with the shortening velocity are quite similar in control and with increased [P_i]. The model reproduces the progressive reduction, with the reduction in load, of the inhibitory effect of P_i on both the mechanical output (Fig. 6C) and the rate of ATP utilization (Fig. 7E), as a consequence of the fact that the increase, with increasing [P_i], in the second order rate constant of the reversal of P_i release (k₋₄[P_i]) becomes progressively less effective due to the strain-dependent rise of the rate constants for the M₁–M₄ transitions. The larger inhibitory power of increased [P_i] on the isometric force, combined with the presence of the early detachment (step 6) followed by product release, is the cause of the large energetic cost of the isometric contraction at high P_i. In fact, as shown in Fig. 7I, the ratio R of the ATPase rate per myosin motor at 10 mm P_i and in the control is 1.3 in the isometric contraction and drops rapidly to 1 with the increase in shortening speed.

Glossary

A

actin monomer to which a myosin motor attaches

A′

actin monomer next to A farther from the centre of the sarcomere

CSA

cross-sectional area

hs

half-sarcomere

M

myosin motor

n

number of attached motors

P_i

inorganic phosphate

Additional information

Conflict of interest

None declared.

Author contributions

All the experiments were performed at the Laboratory of Physiology, Department of Biology, University of Florence, Italy. The following authors participated in performing the experiments, data collection, analysis and interpretation, and drafting the article: M.C., L.M., M.D., V.L. and M.L. The following authors contributed to the conception and design of the experiments and critically revising the article for important intellectual content: V.L. and M.L. All authors approved the final version of the manuscript.

Funding

This work was supported by Ministero dell’Istruzione, dell’Università e della Ricerca (MIUR, PRIN 2011), Ente Cassa di Risparmio di Firenze and Telethon (GGP12282, 2012), Italy.

Supplementary material

Supplemental Material

Supplemental Table S1

Supplemental Fig. S1

Supplemental Fig. S2

Supplemental Fig. S3