Figure 3.

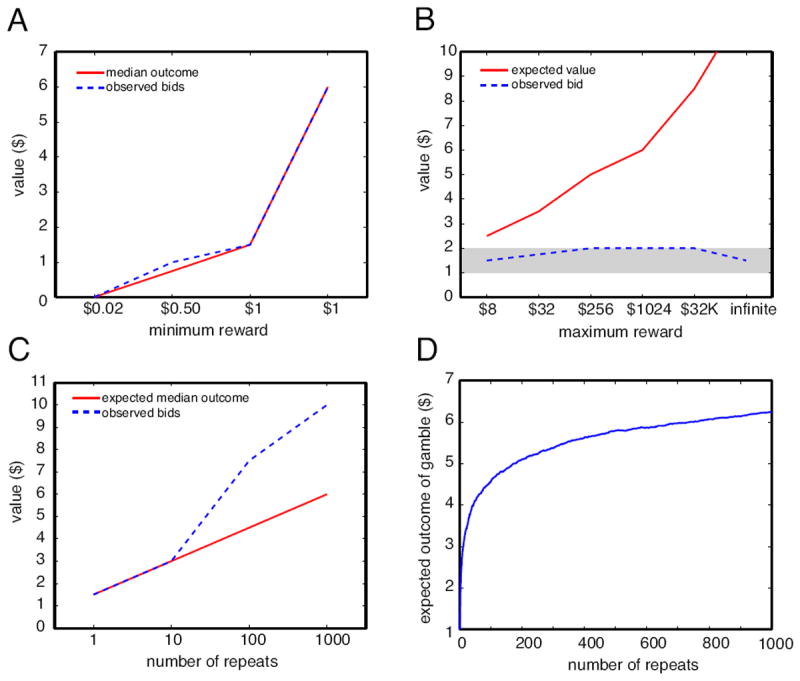
Bids in variants of the St. Petersburg paradox.

A. When the stakes are varied, bids (blue dashed line) closely track the median (red solid line). Expected value (mean) is infinite for all variants.

B. When the St. Petersburg gamble is truncated, the median remains $1.50 (gray shadow), but the mean grows with the truncated value. Bids remain low, close to the median. The standard St. Petersburg gamble has an infinite expected value, and is the rightmost point on the graph.

C. As the St. Petersburg gamble is repeated, offered bids per gamble grow. The offer bids closely tracks, but overestimates, the expected median value of the series of gambles. Means do not change as the gamble is repeated.

D. Median outcome per gamble of repeated St. Petersburg gamble increases as a function of number of repeats. The more repeats the gambler faces, the greater the value of each gamble. Although the function is concave, it is unbounded.