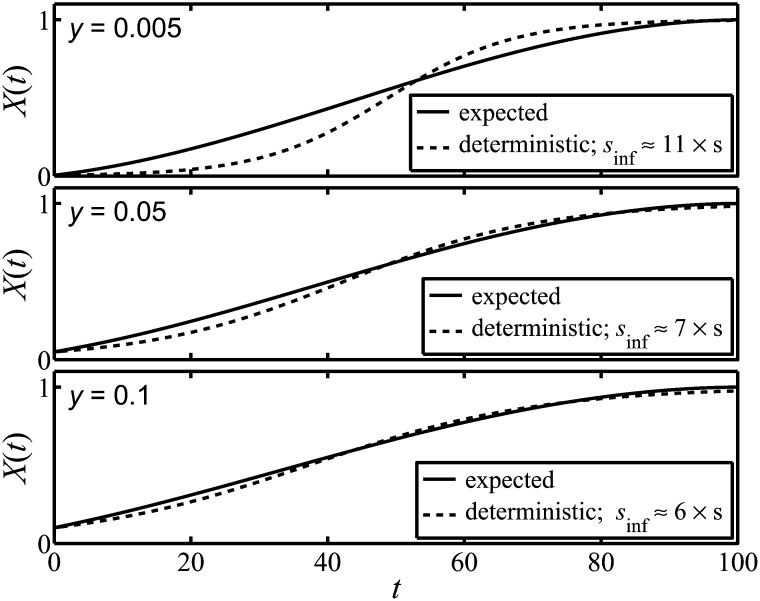
Figure 5.

We show the expected trajectory $\overline{X}\left(t\right)$ of a finite population with N = 100 and the most closely corresponding deterministic trajectory of an infinite population, X_inf(t), in which there is additive selection. The form of X_inf(t) follows from choosing the optimal value of the constant selection coefficient s_inf of the additive selection. The different panels correspond to different values of the initial frequency, y, and the greatest difference between the expected and deterministic trajectories occurs at the lowest values of y. The behavior of X_inf(t) is determined by the initial frequency and the value of s_inf. As a consequence it does not reach the value of unity at the time, T, by which the expected trajectory achieves fixation.