Absolute cross section for low-energy-electron damage to condensed macromolecules: A case study of DNA

Abstract

Cross sections (CSs) for the interaction of low-energy electrons (LEE) with condensed macromolecules are essential parameters for accurate modeling of radiation-induced molecular decomposition and chemical synthesis. Electron irradiation of dry nanometer-scale macromolecular solid films has often been employed to measure CSs and other quantitative parameters for LEE interactions. Since such films have thicknesses comparable with electron thermalization distances, energy deposition varies throughout the film. Moreover, charge accumulation occurring inside the films shields a proportion of the macromolecules from electron irradiation. Such effects complicate the quantitative comparison of the CSs obtained in films of different thicknesses and limit the applicability of such measurements. Here, we develop a simple mathematical model, termed the molecular survival model, that employs a CS for a particular damage process together with an attenuation length related to the total CS, to investigate how a measured CS might be expected to vary with experimental conditions. As a case study, we measure the absolute CS for the formation of DNA strand breaks (SBs) by electron irradiation at 10 and 100 eV of lyophilized plasmid DNA films with thicknesses between 10 and 30 nm. The measurements are shown to depend strongly on the thickness and charging condition of the nanometer-scale films. Such behaviors are in accord with the model and support its validity. Via this analysis, the CS obtained for SB damage is nearly independent of film thickness and charging effects. In principle, this model can be adapted to provide absolute CSs for electron-induced damage or reactions occurring in other molecular solids across a wider range of experimental conditions.

I. INTRODUCTION

Electron interactions leading to molecular decomposition and synthesis within condensed matter are of relevance to problems in diverse fields such as biophysics [1–4], astrophysics and chemistry [5–7], nanotechnology [8–10], and material and environmental sciences [11–14]. Both analytical and Monte Carlo simulation methods are usually employed to quantitatively model the complex sequences of electron-induced processes occurring in condensed media. Such simulations require cross section (CS) values as input data to describe all the collisions made by the primary and all secondary electrons with the molecules of the solid or liquid under consideration [15,16]. Thus, considerable experimental and theoretical efforts have been directed to determining elastic and inelastic electron scattering cross sections for a wide range of molecules encountered in condensed media. Much of the available experimental data derives from gas-phase electron-molecule collision measurements that are free from multiple-scattering effects and for which the initial and final states of the electron-target system are well characterized. However, there exist two main issues related to use of gas-phase data for condensed-phase simulations: (1) macromolecules such as polymers are not easily vaporized without molecular decomposition for gas-phase measurements [17], and (2) electron-molecule scattering CSs can change upon condensation due to interactions among the molecules, molecular ordering, and band structure effects [18–20].

At the theoretical level, models have been developed to determine scattering CSs in the condensed phase [21–23]. For moderate- and high-energy electrons, the models provide relatively accurate values for the CSs [24,25], since the interactions of these electrons with the condensed matter arise through individual localized processes occurring at the atomic level and separated by mean free paths (MFPs) much larger than the atomic dimension. In fact, such conditions are similar to those of gas-phase measurements. In contrast, at low energy (0–100 eV) the electrons have wavelengths comparable to the distance between the target molecules, and hence they interact with the condensed medium through delocalized processes predominantly including static and correlation interactions with neighboring molecules, excitation transfer, and coherent scattering [26–29]. Even though theoretical models have tried to approximate these processes and then transfer the CS data obtained from gas-phased measurements to the condensed-phase conditions, such calculated CSs differ substantially from the available experimental data [29–32].

Several experimental techniques have been developed to measure various CSs and MFPs for low-energy-electron (LEE) interactions within condensed matter [33]. In these techniques, molecules or compounds are deposited on a metal substrate by vapor condensation, sublimation, molecular self-assembly (MSA), and freeze drying (lyophilization). A flux of LEEs, provided by an external electron source under ultrahigh-vacuum (UHV) conditions or generated by x-ray absorption in the underlying metal substrate, is made to pass through the molecular solid film. Following LEE exposure or irradiation of the film, the analysis of the products is performed via two general strategies. The first consists in the measurement of the energy, intensity, and direction of the backscattered and/or transmitted electrons by the techniques of low-energy-electron transmission, electron-energy-loss (EEL), and low–energy-photoelectron transmission spectroscopies [34,35]. The second is the quantification of the molecular alterations such as decomposition or dimerization of the irradiated film by methods of x-ray photoelectron spectroscopy, electron-simulated desorption, liquid chromatography, mass spectrometry, and gel electrophoresis [35,36]. While these techniques provide valuable information on LEE interactions with condensed matter, most of the measured CSs are effective, as they are dependent on the experimental conditions. Therefore, there is an essential need to improve both theoretical and experimental methods for obtaining scattering CSs for LEEs in condensed matter.

One approach to determine absolute CSs of LEE interaction with condensed molecules is to perform a two-stream multiple-scattering analysis of the backscattered electron energy distribution measured by electron-energy-loss spectroscopy [29,30,37,38]. As a first step, entire EEL spectra along with the transmitted currents are measured at different molecular coverages for a fixed incident energy. From the linear relationship found between the energy-integrated EEL spectra and the corresponding transmitted currents, a differential incident electron current is established. The intensity scales of the EEL spectra are then normalized to this current so that the area under an elastic and inelastic feature can be expressed in terms of an absolute reflectivity. When the film thickness is smaller than the MFP of the incident electron (i.e., the single-collision regime), the same area with the knowledge of the molecular coverage gives immediately the absolute CS for electrons backscattered over the whole half angular space [29,38]. In the case of isotropic scattering, the latter amounts to half of the integral CS. When the film thickness is comparable to or larger than the MFP of the incident electron (i.e., the multiple-collision regime), the energy-dependent elastic electron reflectivity (i.e., electron scattered elastically) measured as a function of the film thickness leads to the absolute value of the energy-dependent total CS (i.e., the inverse MFP) [30,37]. The latter is then used to normalize the relative elastic and inelatic integral CSs, which are obtained relative to the total CS from a detailed two-stream multiple-scattering analysis of the EEL spectra. Since such measurements of the absolute CS are limited in practice to films whose thicknesses may range from one to about three times the MFP of the incident electron, they cannot be performed with aggregates of macromolecules at film thicknesses already much larger than the expected electron MFP.

Nanoscale thin solid films of macromolecules are usually prepared via MSA and lyophilization techniques [39–41]. Although both techniques provide thin macromolecular films suitable for studying LEE interactions, each method has some weakness that may affect the results of LEE-macromolecule scattering experiments. While films formed by MSA techniques have a superior uniformity to those prepared by lyophilization, they invariably contain some additional molecular species or molecular modifications which are necessary to bind the macromolecules together or onto the substrate. Such additions or modifications may affect the macromolecule conformation and modulate the damage induced by LEEs [42]. In contrast, by lyophilization, it is possible to prepare pure films of macromolecules or in controlled mixtures with other molecules such as potential radiosensitizers [43,44]. However, the main disadvantage is the ill-defined morphology of the films [45,46], since the films have irregular thickness and uniformity due to the formation of macromolecular aggregates. Nevertheless, lyophilization has been a useful technique for studying the effect of LEEs on condensed matter [47,48].

So far, the CSs of LEE-induced damage to a supercoiled plasmid DNA have been estimated merely by measuring the percentage of the loss of supercoiled (SC) DNA as a function of irradiation time t (i.e., the exposure-response curve) and by quantifying configurational changes of the plasmid [49]. The SC DNA changes to circular and linear forms following single and double strand breaks (SBs), respectively. However, with a double helix diameter of about 2–3 nm, a SC DNA molecule is already comparable to or larger than the expected MFP of LEEs. Therefore, such large molecules in the topmost part of a heterogeneous film hide those located behind them from the incoming electrons. This phenomenon is akin to an attenuation length (AL) for the incident LEEs inside the film and thus limits the LEE-induced damage to a fraction of the film. Besides, most of the LEEs suffer energy loss inside the DNA molecules and end up in intermolecular traps, or via dissociative electron attachment (DEA) stabilize as atomic or molecular anions leading to film charging [50–54]. Both AL and film charging effects can lead to considerable error in the CS values for the formation of DNA damage if not accounted for in the data analysis.

The present paper introduces a molecular survival model adapted to the phenomenology observed in LEE-irradiation experiments with lyophilized plasmid DNA films. The effect of the AL of LEEs on the calculated exposure-response curve is investigated as a function of the film thickness. The exposure-response curve for a given AL of the LEEs and film thickness is simulated in absence and gradually the presence of film charging. Absolute CS values of LEE-induced damage that account for the AL and film charging effects are obtained from experiments with lyophilized plasmid DNA films irradiated with 10 and 100 eV electrons. Finally, using the AL values found in the present work, a penetration factor is introduced to allow comparison with previous CS measurements.

II. EXPERIMENTAL METHOD

The experimental details of sample preparation, irradiation, and postirradiation analysis techniques employed in the present studies have been reported in detail elsewhere [55,56]. Here, we provide only a brief description of the most pertinent elements.

Plasmid DNA [pGEM-3Zf(–), 3197 base pairs, ca. 1 968 966 amu per plasmid] was extracted from Esherichia coli JM109 and purified with a HiSpeed plasmid Maxi kit (QIAGEN). The purified plasmid DNA consisted of 97% supercoiled, 2% concatemeric, and 1% nicked circular forms. The concentration of DNA and the relative quantity of proteins in the plasmid DNA solution was then calculated by measuring the ratio of ultraviolet (UV) absorption of DNA and protein at 260 and 280 nm, respectively, with a Synergy HT-I spectrophotometer. The ratio was 1.99 which corresponds to a purity greater than 95% [57]. The tris(hydroxymethyl)aminomethane (Tris)—ethylenediaminetetraacetic acid (EDTA) (TE) buffer (10 mM/1 mM) was separated from DNA by gel filtration with a Sephadex G-50 medium. Thus, the final solution consisted of DNA and distilled deionized (DD) H₂O after the filtration.

The solution of pure DNA was split into four parts and each of them further diluted in DD H₂O to obtain the concentrations of 30, 45, 60 and 90 ng/μl DNA. To make 5–15 monolayer (ML) films of plasmid DNA, 7 μl of the DNA solutions was deposited onto clean tantalum (Ta) substrates (7 × 20 mm²). The latter consisted of a thin layer (450 ± 50 nm) of Ta sublimated onto either a 0.4-mm-thick silicon wafer or clean borosilicate glass. Then the deposited DNA samples were first frozen at − 65 °C for 10 min in a glovebox and then dried under a pressure of about 6 mTorr by a hydrocarbon-free turbomolecular pump for 2 h to form solid films. The DNA films were circular in shape with an average radius r = 2 mm (±5%). Using the known density ρ = 1.7 g/cm³ (±5%) for the plasmid DNA extracted from E. coli and the masses m of 210, 315, 420, and 630 ng (±10%) of DNA contained in the 7 μl drops deposited on Ta prior to lyophilization, their average thicknesses h = m/π r² ρ were calculated to be 10, 15, 20, and 30 nm with an uncertainty of ±13%.

After preparation, the DNA films were placed on sample holders inside a UHV chamber equipped with an electron irradiator. The latter consists of an electron gun producing a beam adjustable in energy between 5 and 1000 eV. The spot size of the beam can be varried between 2 and 50 mm at working distances of 10 and 50 mm. In the present experiment, it was set to irradiate an area of about 0.9 cm² which was seven times larger than the DNA sample. The chamber was evacuated for 24 h by a hydrocarbon-free turbomolecular pump to a pressure of 5 × 10⁻⁹ Torr at room temperature.

After stabilization of the electron-beam current at 2 nA (±5%) [56], corresponding to the current density of 9.95 × 10¹⁰ electrons s⁻¹ cm⁻², the DNA films were individually irradiated with electrons of either 10 or 100 eV for periods between 5 and 90 s. While bombarding a sample, the others were shielded from stray electrons by applying a repulsive potential of 9 V with respect to the cathode of the electron gun. A sample in the UHV chamber was never irradiated with electrons to serve as a control.

After irradiation, the samples were removed from the chamber and immediately dissolved in 10 μl of TE buffer at pH 8.0. A comparison of the amount of recovered DNA with the original solution used for DNA deposition showed that nearly 98% of the deposited DNA was recovered from the substrate. The separation of the different structural forms of DNA, such as SC, nicked circular, linear, etc., in the samples was performed by agarose gel electrophoresis. The DNA samples and the agarose gels were stained with SYBR Green I in concentrations of 100 times and 10 000 times, respectively. The samples were passed on 1% agarose gel in 1 times Tris—acetic acid—EDTA (TAE) buffer at 100 V for 7 min followed by 75 V for 68 min (5 V cm⁻¹). The gels were then scanned by Typhoon-Trio laser scanner (from GE Healthcare) adjusted for the blue fluorescent mode at an excitation wavelength of 488 nm and filter type 520 nm bandpass (520 BP 40) in the normal sensitivity mode. The amount of each structural form of the DNA was analyzed by IMAGEQUANT (Molecular Dynamics) software. To achieve a better accuracy, the binding efficiencies of SYBR Green I for the same amount (75 ng) of SC and linear DNA were measured to establish a correction factor. This factor, which arises from the weaker binding of SYBR Green I to supercoiled DNA than to the nicked circular and linear forms, was 1.2 and was applied to the quantification of the different structural forms of plasmid DNA.

III. MOLECULAR SURVIVAL MODEL

Molecular damage such as DNA SBs results from the inelastic interactions of incident electrons with macromolecule subunits and may involve ionization, excitation, and the formation of negative ions, leading to the rupture of bonds within and between the constituents [55,56,58,59]. Elastic and inelastic collisions contribute to the spread of an incident electron beam within a film. Surface analysis of multilayer films by x-ray photoelectron spectroscopy shows that the decrease in electron intensity depends exponentially on the thickness of the films [60–63]. Similarly, for a monoenergetic incident electron beam with a uniform surface current density J₀ impinging on a molecular film of thickness h, the surface current density J(x) at a depth x inside the film is given simply by

$$J(x)=J_0{e}^{-x/\lambda },$$ (1)

where λ is defined as the AL.

Let q(x,t) be defined as the relative proportion of intact molecules (e.g., SC DNA) within an infinitesimally thin slab between x and x + dx after an irradiation time t. The value of q(x,t) is unity when there is no molecular damage at t = 0 and decreases toward zero with t. Integrating q(x,t) over the whole film thickness between 0 and h gives the total percentage of intact molecules in the film at a given t:

$$P(t)=P_0\frac{1}{h}{\int }_0^{h}q(x,t)dx,$$ (2)

where P₀ is the percentage of intact molecules in the nonirradiated film. The function q(x,t) is solution of

$$dq(x,t)=-\sigma J(x)q(x,t)dt,$$ (3)

where σ is the CS to damage a molecule by LEE impact (e.g., loss of SC DNA). By substituting the right-hand side of Eq. (1) into Eq. (3) and using the initial condition q(x,0) = 1, Eq. (3) is readily solved as

$$q(x,t)=e^{-\sigma J_{0}t{e}^{-x/\lambda }}.$$ (4)

By substituting the above expression for q(x,t) into Eq. (2), p(t) becomes

$$P(t)=P_0\frac{1}{h}{\int }_0^h{e}^{-\sigma J_{0}t{e}^{-x/\lambda }}dx.$$ (5)

It is also possible to algebraically solve the integral with the following change of variables:

$$\begin{array}{l}z=e^{-x/\lambda }\text{and}dz=-\frac{z}{\lambda }dx,\\ P(t)=P_0\frac{-\lambda }{h}{\int }_1^{e^{-h/\lambda }}\left(\frac{e^{-\sigma J_{0}tz}}{z}\right)dz.\end{array}$$ (6)

Expanding the numerator of the integral in series around t = 0 and integrating each term separately, the solution of Eq. (6) can be written as

$$P(t)=P_0\left[1-f_1\frac{(\sigma J_0)}{1!}t+f_2\frac{{(\sigma J_0)}^2}{2!}{t}^2-f_3\frac{{(\sigma J_0)}^3}{3!}{t}^3+\cdots \right],$$ (7)

where

$$f_n=\left(\frac{\lambda }{nh}\right)(1-e^{-nh/\lambda }),$$

with n = 1,2,3,…. Equation (7) gives the total percentage of intact molecules in the film following an irradiation time t. For a sufficiently small t, the expression for P(t) reduces to the first two terms

$$P(t)=P_0-P_0{f}_1\sigma J_{0}t=P_0-P_0\sigma J_0\left(\frac{\lambda }{h}\right)(1-e^{-h/\lambda })t,$$ (8)

with P(t) varying linearly with t along with the proportionality constant depending on P₀, σ, J₀, λ, and h. It should be noted that λ is connected with the total CS and density of the material and therefore depends implicitly on σ. However, with the present model λ and σ can be determined separately.

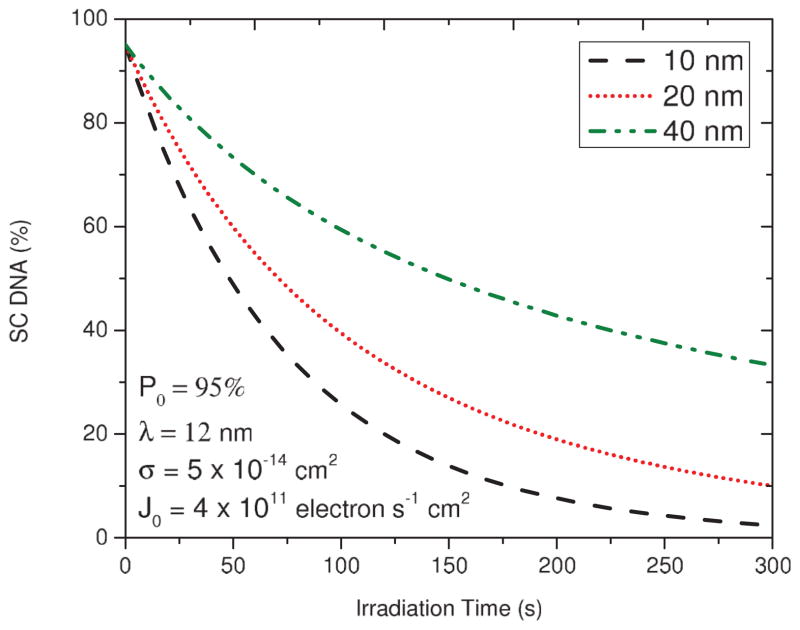
The simulated exposure-response curves derived from Eq. (5) for solid DNA films of 10, 20, and 40 nm for a fixed λ of 12 nm and σ of 5 × 10⁻¹⁴ cm² are plotted in Fig. 1. The dependence of the initial slopes on h indicates that the rate of SC loss decreases with the film thickness. From the calculated curves, the fraction of DNA in the SC forms is expected to decrease quasiexponentially to zero with increasing t. However, this behavior differs from the experiments in which the exposure-response curves reach finite levels [55,56]. These saturation effects are the result of charge accumulation within the irradiated films (i.e., film charging).

FIG. 1.

(Color online) Simulation of exposure-response curves for loss of the SC DNA based on Eq. (5) for three different DNA film thicknesses of 10, 20, and 40 nm and for a fixed AL in the absence of film charging.

Film charging is an inevitable consequence of the irradiation of a thick molecular solid film with LEEs. Such films can charge negatively or positively depending on the relative proportion of secondary-electron emission, ionization, electron thermalization, and DEA processes. For electron irradiation at an energy less than that required for ionization, electron trapping leads to the accumulation of negative charges in the films. Previous studies have shown that a submonolayer of molecules deposited onto the surface of a dielectric film deposited onto a metallic substrate can trap electrons and thus generate a negative potential acting as a barrier for the incoming electrons [50,64–67]. The magnitude of this potential barrier depends on the accumulated charge density and its distance from the metallic substrate (i.e., the thickness of the dielectric layer L). For small L, the charges are close to the substrate and therefore only a small potential barrier is generated, whereas for large L the charge is far from the substrate, resulting in a much larger potential. When considering molecular solids, such as lyophilized DNA, and the condition h > λ, one expects an accumulation of negative charges in the topmost part of the film far from the metallic substrate, thus giving rise to a large repulsive potential.

Lyophilized films of macromolecules such as DNA have thickness irregularities due to aggregation. When the incident electrons get trapped within relatively thick aggregates, they give rise to a large repulsive potential even if the rest of the film shows very few charges. This repulsive potential, which increases with the electron irradiation time, subsequently repels the incoming electrons. When considering the random accumulation of charges over a film surface, the number of sites accessible to the incident electrons (i.e., noncharged sites) should decrease exponentially upon electron irradiation time. Consequently, the electron density J₀ impinging on the film can be considered to decrease exponentially with the irradiation time.

Under these conditions, the charging effect can be simply accounted for by modifying Eq. (1) as follows:

$$J(x,t)=J_0{e}^{-x/\lambda }{e}^{-t/\tau },$$ (9)

where τ is a charging time constant that characterizes the decrease of J₀ with the irradiation time t. When τ → ∞ or if t ≪ τ, as might be the case with the thinnest films, Eq. (9) reduces to Eq. (1) in the absence of charging conditions. So in the presence of charging, q(x,t) and P(t) are rewritten as

$$q(x,t)=e^{-\sigma J_0\tau (1-e^{-t/\tau })e^{-x/\lambda }}$$ (10)

and

$$P(t)=P_0\frac{1}{h}{\int }_0^h{e}^{-\sigma J_0\tau (1-e^{-t/\tau })e^{-x/\lambda }}dx.$$ (11)

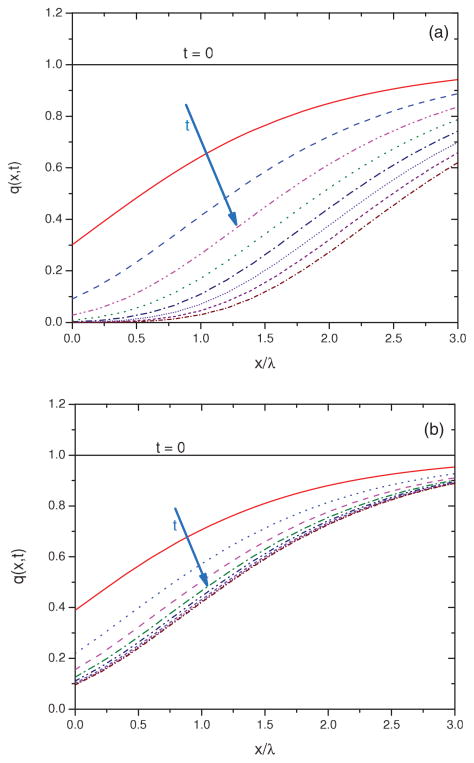
In Fig. 2(a), Eq. (10) is used to simulate how q(x,t) varies within a film in the absence of charging (i.e., τ → ∞) and in Fig. 2(b) in the presence of charging. Each solid line in the figure corresponds to q(x,t) after a given irradiation time. In the case of zero charging and for x ≪ λ, q(x,t) decreases rapidly with irradiation time. Deeper within the film, as x > λ, a relatively smaller fraction of the target molecule (SC DNA) is lost upon electron irradiation. When the charging effect is included in the calculation [Fig. 2(b)], the number of accessible sites is further reduced, and the molecular damage is restricted to a much smaller fraction of the film, close to x = 0.

FIG. 2.

(Color online) Simulation of the normalized number of SC DNA in various depths of a DNA film at different irradiation times (t) in absence of charging (a) and in presence of charging (b).

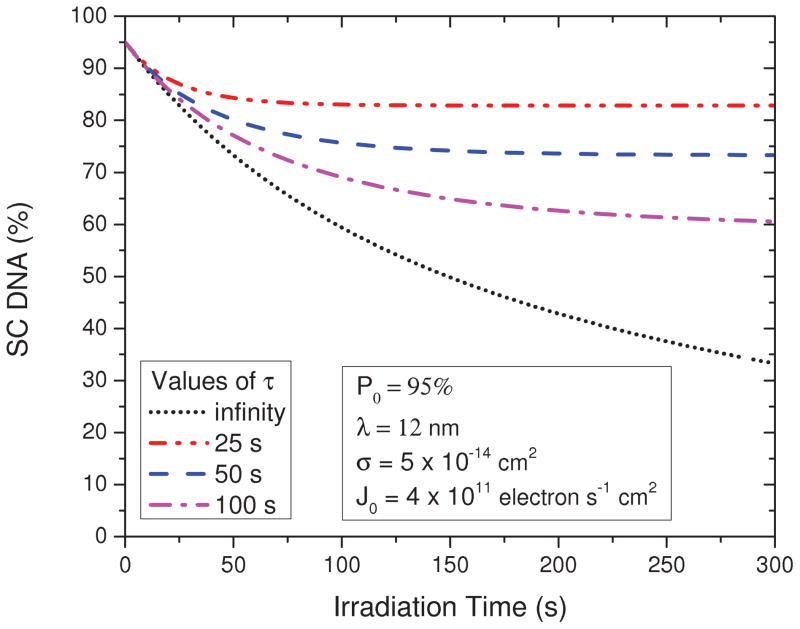
Figure 3 shows how P(t) calculated from Eq. (11) varies as a function of the irradiation time t for a 40-nm-thick DNA film given different charging time constant τ, and with the values of P₀, σ, J₀, and λ the same as Fig. 1. As might be anticipated, the smaller the value of τ, the larger the asymptotic value of P (t) at long t and the shorter the time required for P (t) to reach this saturation value. In other words, the more quickly the film charges, the smaller the fraction of the film that is irradiated and the smaller the loss of SC DNA. On the other hand, the slopes of the curves for different τ at t = 0 are found to be the same. Therefore, the rate of decrease of the initial concentration of the target molecules is in principle independent of the film charging. In other words, for sufficiently short irradiation time, the charging should have the least effect on the slope of the exposure-response curve and should still be given by [cf., Eq. (8)]

FIG. 3.

(Color online) Simulation of the exposure-response curves for loss of SC DNA in a 40-nm-thick film for different charging time constants (τ).

$$P^{\prime }(0)=-P_0\sigma J_0\left(\frac{\lambda }{h}\right)(1-e^{-h/\lambda }).$$ (12)

IV. RESULTS AND DISCUSSION

A. AL and CS for DNA strand breaks at 10 and 100 eV

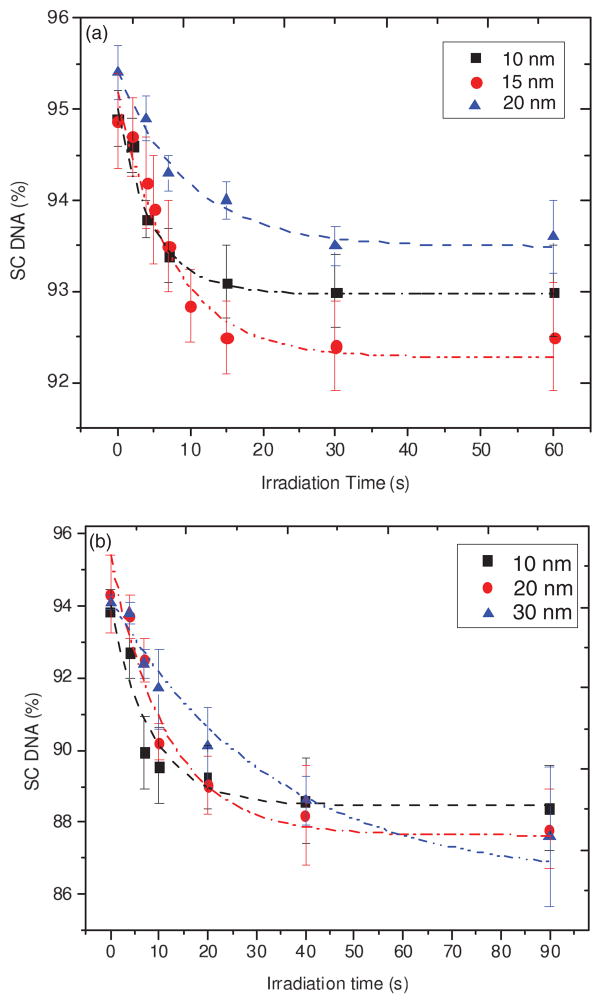
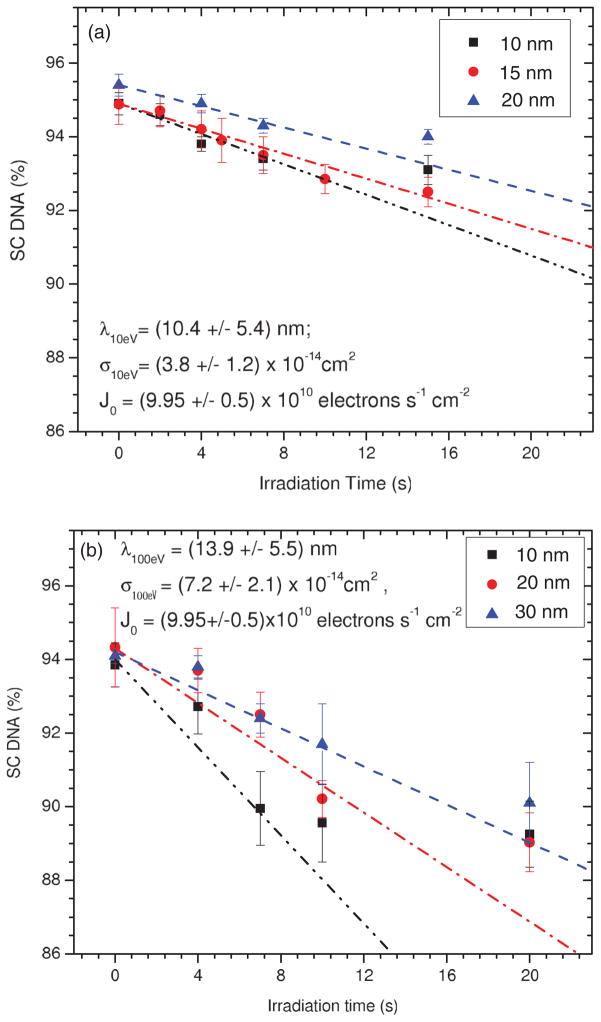
Figure 4 presents the measured percentage loss of SC DNA as a function of irradiation time t (i.e., exposure-response curves) for 10–30-nm-thick lyophilized pure DNA films exposed to monoenergetic electrons of 10 and 100 eV. As expected, the proportion of DNA in the SC form decreases with t as it is primarily transformed into nicked circular and linear forms via the induction of single and double SBs, respectively. As in the simulations in Figs. 1 and 3, the initial portions of the measured exposure-response curves at short t exhibit a nearly linear behavior whose slope becomes less steep as h is increased. The values of these slopes obtained using only points up to 10 s are, respectively, 0.23 ± 0.03, 0.2 ± 0.02, and 0.15 ± 0.02 s⁻¹ for the 10, 15, and 20 nm films exposed to 10 eV electrons, and 0.47 ± 0.1, 0.37 ± 0.09, and 0.27 ± 0.05 for the 10, 20, and 30 nm films exposed to 100 eV electrons. At large t, each curve reaches a saturated level due to the effect of a finite AL and the film charging effect. These results are in good agreement with the characteristics expected for exposure-response curves by our model (Fig. 3). These correspondences provide assurance that CS and AL values can be deduced from the experimental data by employing the proposed molecular survival model.

FIG. 4.

(Color online) Exposure-response curve for lyophilized plasmid DNA films of 10, 15, and 20 nm average thickness, irradiated with 10 eV electrons (a) and 10, 20, and 30 nm average thickness, irradiated with 100 eV electrons (b). The dash-dotted lines are guides for the eye. Each data point corresponds to the mean value of three samples with the relevant standard deviation.

Using Eq. (12), λ can be determined from the ratio R_1,2 of the initial slopes $P_1^{\prime }(0)$ and $P_2^{\prime }(0)$ of the exposure-response curves between two different thicknesses h₁ and h₂:

$$\begin{array}{l}{R}_{1,2}(\lambda )=\frac{P_1^{\prime }(0)}{P_2^{\prime }(0)}=\frac{-P_{01}\sigma J_0\left(\frac{\lambda }{h_1}\right)(1-e^{-h_1/\lambda })}{-P_{02}\sigma J_0\left(\frac{\lambda }{h_2}\right)(1-e^{-h_2/\lambda })}\\ =\frac{-P_{01}{h}_2(1-e^{-h_1/\lambda })}{-P_{02}{h}_1(1-e^{-h_2/\lambda })}.\end{array}$$ (13)

Since $P_1^{\prime }(0),P_2^{\prime }(0)$, P₀₁, P₀₂, h₁, and h₂ are the known experimental parameters, it is possible to obtain a statistical average value for λ by repeating the analysis for all possible pairs among the three thicknesses studied in our experiment. Once λ and its uncertainty are determined, then σ is readily obtained from Eq. (12).

Table I presents the ratios of the initial slopes obtained between all possible pairs h₁ and h₂ among the 10, 15, and 20 nm films at 10 eV and 10, 20, and 30 nm films at 100 eV along with the corresponding deduced values of λ and their statistical uncertainties from Eq. (13). We observe that at both incident electron energies, the ratios of initial slope yield progressively smaller λ values as the film thickness increases. By comparing the effect of a finite λ on the loss of SC DNA with electron exposure in Figs. 1 and 3 (i.e., the effect of film charging), we further note that within a given range of exposure, a decrease in λ and increase in charging rate produce a similar effect; that is, they both act to reduce the size of any loss of SC DNA. It is therefore suggested that the trend of decreasing λ values with larger film thicknesses reflects film charging. Because of this effect, we report in Table I the average values of λ at 10.4 ± 5.4 and 13.9 ± 5.5 nm for 10 and 100 eV electrons by including an additional systematic error of ±50% and ±30% nm, respectively.

TABLE I.

Values for the ratios R_1,2(0) of the initial slope of the exposure-response curves between all possible thickness pairs h₁ (nm) and h₂ (nm) among the 10, 15, and 20 nm films at 10 eV, as well as the 10, 20, and 30 nm films at 100 eV. Corresponding values of the AL in the plasmid DNA, λ (nm), deduced from Eq. (13) along with the calculated average. SE is the standard error.

10 eV				100 eV
h1	h2	R1,2(0)	λ	h1	h2	R1,2(0)	λ
10	15	1.15 ± 0.2	16.0 ± 3.7	10	20	1.27 ± 0.4	18.1 ± 6.8
10	20	1.47 ± 0.3	9.8 ± 3.7	10	30	1.74 ± 0.5	14.0 ± 5.9
15	20	1.28 ± 0.2	5.5 ± 3.6	20	30	1.37 ± 0.4	9.7 ± 6.1
		Average ± SE	10.4 ± 5.4			Average ± SE	13.9 ± 5.5

Given the average λ, we present in Table II the values for σ calculated from Eq. (12) for the DNA films of three different thicknesses irradiated with 10 and 100 eV electrons. The resulting uncertainty for each value depends on that of the initial slope P′ (0) in the ranges of ±10% to 13.3% and ±17% to 24% for 10 and 100 eV electrons, respectively, the percentage of the SC DNA in the nonirradiated samples P₀ at ±1%, the film thickness h at ±13%, and the average λ at ±52% and 39% for 10 and 100 eV, respectively. The average values σ for three films are (3.8 ± 1.2) × 10⁻¹⁴ and (7.2 ± 2.1) × 10⁻¹⁴ cm² for 10 and 100 eV electrons. Their uncertainties are obtained based on the weighted mean and the error in the mean [68]. In Fig. 5, the initial slopes based on the average values for σ and λ at 10 and 100 eV electrons are compared and fitted to the experimental data.

TABLE II.

Cross section σ (10⁻¹⁴ cm²) to induce a SB in plasmid DNA by 10 and 100 eV electron impact on different film thicknesses h (nm). SE is the standard error.

10 eV		100 eV
h	σ	h	σ
10	3.7 ± 2.1	10	7.1 ± 3.8
15	3.9 ± 2.2	20	7.5 ± 3.8
20	3.7 ± 2.0	30	7.1 ± 3.2
Average ± SE	3.8 ± 1.2	Average ± SE	7.2 ± 2.1

FIG. 5.

(Color online) Calculation of the initial slope of the exposure-response curve based on the theoretical model and fitting to the measured data sets for 10 eV (a) and 100 eV (b) electrons.

B. Correction factor

Based on Eqs. (8) and (12), the CS of DNA SBs can be calculated from the initial slope of the exposure-response curve, when J₀ and P₀ are the known parameters. Moreover, the CS should be corrected by the penetration factor f₁ when a DNA film has a thickness comparable to or larger than λ:

$$f_1=\frac{\lambda }{h}(1-e^{-h/\lambda }),$$ (14)

along with

$${\sigma }_{SB}=-\frac{P^{\prime }(0)}{P_0{J}_0{f}_1}.$$ (15)

Equation (15) thus prescribes that both the f₁ factor and the slope of the exposure-response curve at zero dose are essential to determine the CS of DNA SBs, which is independent of film thickness and charging effects.

Table III summarizes the CS data for DNA SB damage measured in this and several other studies by irradiation of dry, nanoscale DNA films with LEEs. The table also contains f₁ calculated for those experiments performed with thick films of DNA, so that the reported CSs per plasmid (σ′) are corrected to new values (σ). The relative errors in f₁ at about 55% and 45% for 10 and 100 eV electrons result from propagating in Eq. (14) the uncertainty in λ and h [68]. For 10 eV electrons, the present CS is similar to those recorded by Panajotovic et al. [56] and Boulanouar et al. [69], and is slightly larger relative to that measured by Dumont et al. [70]. To compare the results obtained from thick and thin films, the σ are normalized to the CS per nucleotide (σ_n) for the induction of SBs. Cai et al. [61] and Dugal et al. [71] directly measured σ_n via irradiation of a self-assembled monolayer (SAM) oligonucleotide film with LEEs. For 10 eV electrons, the present value of σ_n is in a good agreement with those measured directly at 8, 9, and 12 eV electrons by Cai et al. and Dugal et al. These results suggest that the penetration factor f₁ is a crucial parameter in obtaining the CS of DNA SB damage independent of the thickness of the lyophilized films, particularly when the average thickness of the DNA film is comparable with the AL of the incident electrons. This factor however has a limit. As the film thickness increases or λ decreases, film charging can affect substantially the initial slope of the exposure-response curves, even at short irradiation times. In our study, this effect is observed for 30 nm films irradiated with 10 eV electrons. Under this condition, Eq. (12), which is in fact obtained from the first two terms of the algebraic solution of Eq. (11), is no longer accurate for calculation of the AL and CS from the measured data set. To employ Eq. (12) and f₁ with the experimental data set, it is suggested that one consider the ratio of the film thickness to the AL of the incident electrons (h/λ). For 10 eV electrons, for example, the applicability of Eq. (12) is restricted to h/λ ≤ 2 for the plasmid DNA films, i.e., for thicknesses up to 20 nm. Beyond the ratio, it is suggested that one consider other terms of the solution of Eq. (11) by which the initial slope P′(0) depends on the charging time constant τ in addition to the other parameters mentioned in Eq. (12).

TABLE III.

Present and previous CS data needed to induce SB in DNA by LEE impact. The f₁ value is the penetration factor used to correct the measured CS obtained from thick films. σ′ (10⁻¹⁴ cm²)and σ (10⁻¹⁴ cm²) present the measured CS per plasmid for loss of SC before and after applying f₁, respectively. σ_n (10⁻¹⁷ cm²) stands for the CS per nucleotide needed to induce DNA SBs. NA indicates not applicable.

Reference	Film medium	Film preparation method	Electron energy (eV)	Film thickness (nm)	f1	σ′	σ	σn
This study	Plasmid DNA	Lyophilization	10	10	0.64 ± 0.35	2.4 ± 0.4	3.7 ± 2.1	0.58 ± 0.32
				15	0.53 ± 0.29	2.1 ± 0.2	3.9 ± 2.2	0.61 ± 0.33
				20	0.44 ± 0.23	1.6 ± 0.2	3.7 ± 2.0	0.57 ± 0.31
This study	Plasmid DNA	Lyophilization	100	10	0.71 ± 0.35	5.04 ± 1.1	7.1 ± 3.8	1.11 ± 0.59
				20	0.53 ± 0.24	3.95 ± 0.98	7.5 ± 3.8	1.16 ± 0.6
				30	0.41 ± 0.17	2.89 ± 0.51	7.1 ± 3.2	1.1 ± 0.49
Panajotovic et al. 2006a [56]	Plasmid DNA	Lyophilization	10	21	0.4 ± 0.2	1.1 ± 0.5	2.7 ± 1.8	0.42 ± 0.26
Dumont et al. 2010 [70]	Plasmid DNA	Lyophilization	10	10	0.6 ± 0.1	0.9 ± 0.1	1.5 ± 0.3	0.23 ± 0.05
Boulanouar et al. 2012 [69]	Plasmid DNA	Self-assembled	10	10, 15, 20	NA	5.2 ± 1.3	NA	0.8 ± 0.2
Cai et al. 2006 [61]	Oligo-nucleotide	Self-assembled monolayer	8	<2	NA	NA	NA	0.3 ± 0.1
			12	<2	NA	NA	NA	1.7 ± 0.5
Dugal et al. 1999 [71]	Oligo-nucleotide	Self-assembled monolayer	9	<2	NA	NA	NA	0.5
			12	<2	NA	NA	NA	0.8

^aThe corrected CS recorded by Panajotovic et al. is for formation of circular DNA which contributes to more than 95% of the loss of SC.

Since the interaction of a LEE with a condensed molecule is affected by the neighboring molecules (e.g., through the processes of target polarization and electron correlation), film morphology may affect the CS measurement. However, the similarity between the CSs of DNA SBs obtained from two different film morphologies in the present study and those measured via self-assembled films of DNA [61,69,71], suggests that film morphology has only a small effect on the CS, when it is corrected for different film thicknesses and charging conditions. Therefore, our model appears as an appropriate tool to measure the CS of DNA SBs under condensed-phase conditions with a negligible effect from film morphology.

It has also been suggested that 10 eV electrons predominantly generate fragmentation in DNA by single events through the process of DEA via core-excited resonances [39,72], whereas 100 eV electrons may cleave DNA by multiple events through nonresonant mechanisms including ionization, excitation, and neutral dissociations [73]. As a result of the multiple events, secondary species such as LEEs can be created by incident 100 eV electrons during their passage through the film. These LEEs can penetrate further into the film to induce more damage to the DNA. Therefore, it is expected that the ALs and CSs of DNA SBs at 100 eV will be larger than those for 10 eV, as observed experimentally. This difference can also be seen in the measured exposure-response curves for 10 and 100 eV electrons (Fig. 4) by comparing their saturation levels, as they are lower at 100 eV than those at 10 eV. However, the CSs for 100 eV electrons slightly increase, by a factor of 1.9, compared to those for 10 eV electrons. This small increase suggests that although the CS for the sum of the ionization and fragmentation channels at 100 eV is reported to be larger by one or two orders of magnitude than that at 10 eV for most organic molecules [74–76], resonant and nonresonant mechanisms have relatively similar contributions to the generation of DNA SBs at both energies. Similar comparisons were also made in previous studies (i.e., the yields for the formation of single and double SBs by 10 and 100 eV electrons had comparable values) [73,77,78]. Therefore, our results confirm the previous suggestion that for a given CS value, the formation of transient anions and DEA are much more efficient processes than others to induce SBs in DNA.

V. CONCLUSION

We have developed a simple molecular survival model to obtain CSs for LEE damage to a macromolecule within a nanoscale-thickness solid film, which takes into account the thickness and charging of the film. It was shown that the slope of the exposure-response curves at short irradiation time decreases with thickness, and yields of damage reach saturation after the degradation of only a few percent of the intact molecule, owing to charge accumulation. Since the CS for molecular damage is directly calculated from such curves, particularly the initial portion of the curves at short exposure times, these effects can cause the CS to be significantly underestimated. Thus, the model allows study of the behavior of the exposure-response curves as a function of film thickness and saturation levels at high exposure. It essentially evaluates the effects of film thickness and charging on the exposure-response curve for a particular damage induced by LEEs.

As a case study, we prepared nanoscale films of pure plasmid DNA via the lyophilization technique and subsequently bombarded them with LEEs at various fluences. The exposure-response curves for induction of DNA SBs was found to strongly depend on the thickness and charging of the films, in agreement with our mathematical model. Based on the latter, the effects of charge accumulation and thickness of the lyophilized films can be ignored, if the initial slope of the exposure-response curves is obtained at zero dose and corrected by a penetration factor. This factor depends on the film thickness and AL of the incident electrons inducing the DNA SBs. Furthermore, the compatibility between the CSs obtained by the model in the lyophilized films and those measured in MSA films of different types of DNA (e.g., oligonucleotide) suggests that film composition and morphology have a minor effect on the CSs. Therefore, this model eliminates the major obstacles that prevent precise quantification of DNA damage and further allows the previously measured CSs to be converted to a CS that is nearly independent of the film thickness and charging effects.

Considering that the measurement of the real absolute CS for the interaction of LEEs with a single DNA molecule is not currently feasible, the present CSs derived herein for condensed DNA films appear to be the most precise quantities yet to describe LEE-induced damage. Moreover, the present model can be adapted to other organic and inorganic macromolecules such as synthetic polymers, nanotubes, graphene, etc., to determine absolute CSs for LEE-induced chemical processes.