Figure 3. The Variable Environment Genetic Algorithm dramatically speeds up the evolution of solutions to the density classification task.

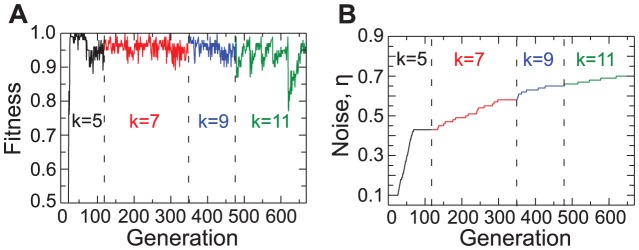
(A) Highest fitness in the population and (B) noise magnitude 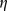as a function generation number. We start simulations with 100 randomly selected populations of agents having genomes with 32 bits, that is, k = 5 and 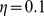. When a genome reaches a fitness of 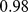, we increase the magnitude of the noise by 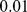. In the beginning of the process the most efficient rules are guessers, that have efficiency about 0.5. At some generation an innovative rule evolves that can classify both kinds of consensus, and in a few more generations the desired efficiency is achieved. The noise then increases rapidly until it reaches a critical level (about 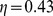). Then, no rule achieves the desired efficiency even after 50 generation. At this point, we promote the population of rules to include extra neighbors. The doted lines in the panels mark these moments. The promoted rules are essentially identical to the previous ones, with the extra neighbors acting as silent inputs, that is, the extra information does not affect the rule dynamics. The GA, by mutation and crossover, should make use of these new inputs to evolve more efficient rules. Eventually, members of the population will achieve the desired efficiency, noisy increases until it reaches another level that can not be surmounted by rules with this value of 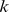. The rules are promoted again, and the process continues with noise and complexity of the rules co-evolving until we obtain highly complex rules (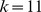) that sustain high noise levels ().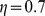