Fig. 11.

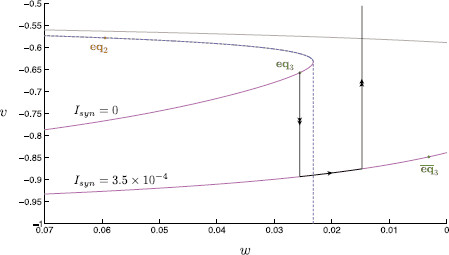
Singular limit analysis of step inhibition. A classical current step protocol is applied to the dimensionless modified propofol model. A geometric singular perturbation analysis is then performed on this system. The synaptic current is held at $I_{\mathrm{syn}}=3.5\times {10}^{-4}$ to simulate inhibition. We compare the critical manifold for each value of $I_{\mathrm{syn}}$. On each manifold, the lower branch (magenta) is linearly stable, the upper branch (gray) linearly unstable. The stable node equilibria (green), ${\mathbf{eq}}_3$ and ${\overline{\mathbf{eq}}}_3$, and saddle equilibrium (orange), ${\mathbf{eq}}_3$ are indicated. Initially, the system starts at rest on the node equilibrium of the $I_{\mathrm{syn}}=0$ critical manifold. At the onset of inhibition, the critical manifold is shifted in the direction of negative w. In the singular limit, the layer problem dictates that the trajectory falls to the lower branch of the critical manifold. Once on the manifold, the reduced problem dictates that the trajectory slowly approaches ${\overline{\mathbf{eq}}}_3$. Once the inhibitory current is removed, the manifold shifts back to its original position, at which point the layer problem determines that the trajectory shoots upward in the direction of positive v. In the singular limit, the threshold manifold (blue dashed) is the concatenation of the middle branch of the critical manifold with the fast fibre through the lower fold of the critical manifold. If the singular limit trajectory passes this manifold, the singular limit predicts a spike event