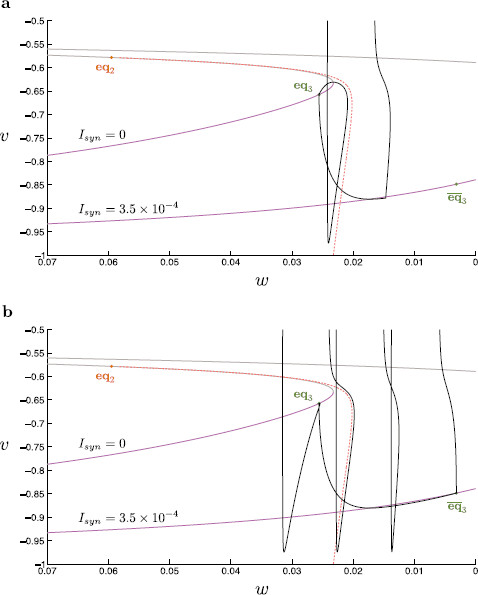
Fig. 12.

Non-singular analysis of step inhibition. A classical current step protocol is applied to the dimensionless modified propofol model for 40 ms, and 250 ms. We compare the critical manifolds (v-nullclines) for $I_{\mathrm{syn}}=0$ and $I_{\mathrm{syn}}=3.5\times {10}^{-4}$. On each manifold, the lower branch (magenta) is linearly stable, the upper branch (gray) linearly unstable. The corresponding stable node equilibria (green), ${\mathbf{eq}}_3$ and ${\overline{\mathbf{eq}}}_3$, and saddle equilibrium (orange), ${\mathbf{eq}}_2$, are indicated. Initially, the system starts at rest at the node equilibrium of the $I_{\mathrm{syn}}=0$ critical manifold. At the onset of inhibition, the manifold is shifted in the direction of negative w. The trajectory falls to the lower branch of the shifted manifold, slowly approaching ${\overline{\mathbf{eq}}}_3$. Once the inhibitory current is removed, the critical manifold shifts back to its original position, at which point the trajectory rapidly shoots in the direction of positive v. The threshold manifold for trajectory spiking is indicated (orange dashed). a If the trajectory passes this separatrix, when released from inhibition, the system spikes. The trajectory is reset with a net shift in the direction of positive w. Upon resetting, the trajectory lies to the left of the separatrix and falls within the basin of attraction of the stable node equilibrium. b As the length of inhibition is increased, the trajectory evolves closer toward the shifted equilibrium position. Here, the trajectory undergoes three spikes before being reset to the left of the separatrix and finally coming to rest. Note the system used here to calculate the threshold manifold makes use of the reduction $\tilde{x}={\tilde{x}}_{\mathrm{\infty }}(v)$, for $x=m,h,n$, in order to allow calculation along the repelling middle branch. Locally (for sub and perithreshold regimes) this reduced system well approximates the modified propofol model, despite being unable to repolarize after a spiking event