Fig. 4.

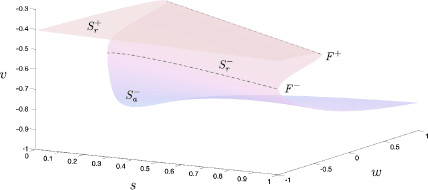
Critical manifold in $(v,w,s)$-space. The critical manifold, $S_0$, is the set of stationary equilibria within the layer problem, (7). This surface defines the interface between fast and slow dynamics: the layer problem describes rapid movement toward or away from $S_0$, the reduced problem describes slower dynamics on the manifold itself. Within a physiologically relevant domain, $S_0$ has a roughly cubic structure, consists of upper and lower fold curves, $F^{+}$ and $F^{-}$ respectively, and three sheets of stationary equilibria. There exists a single lower attracting sheet, $S_a^{-}$, and upper and lower repelling sheets, $S_r^{+}$ and $S_r^{-}$, respectively. On the uppermost surface lies a line of Andronov–Hopf bifurcations from which a family of limit cycles emanate. The line of Andronov–Hopf bifurcations lies out of range while the family of limit cycles terminate within (not shown). Note the shape and stability properties of the critical manifold are independent of ${\tau }_s$