Fig. 6.
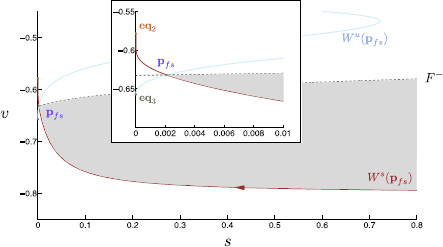
The desingularised reduced problem. The desingularized reduced problem, (15), near the lower fold is projected onto -space. Here, , although the basic structure shown here is common to all values of analyzed. The lower fold curve, (gray dashed), is indicated. The folded saddle, (purple), lies on the fold curve and gives rise to two invariant manifolds: a stable invariant manifold, (red), and an unstable invariant manifold, (blue). The dynamics in -space above are reversed, and so the stable and unstable manifolds have reversed stability properties above . Arrows indicate motion along the invariant manifolds. Each manifold terminates at a stable node equilibrium, within the reduced flow. The stable manifold terminates at on (orange) and the unstable manifold terminates at on (green). Note, if a singular trajectory lands onto the shaded region of , it eventually undergoes a rebound spike. Inset: A magnification of the desingularized reduced problem near the folded saddle
