Fig. 7.

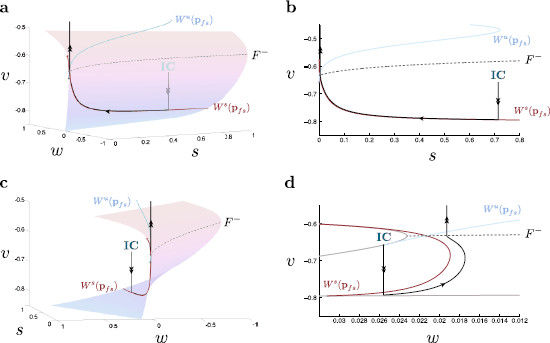
Singular global trajectories in $(v,w,s)$-space. The desingularized reduced problem is projected onto the critical manifold near the lower fold (gray dashed) for ${\tau }_s=15$. Singular solution trajectories from the layer problem, (7), and the reduced problem, (15), are concatenated to produce singular global trajectories (black). a From the initial condition (IC), the layer problem dictates that the singular trajectory falls onto $S_a^{-}$. Since the singular trajectory base point lies within the region bound between the canard separatrix and $F^{-}$, the reduced problem dictates that the trajectory evolves toward the fold curve. At the fold, due to a singular blow up of the reduced problem, the trajectory undergoes fast oscillations within the layer problem. This trajectory corresponds to a successful post-inhibitory rebound spike. b The corresponding system projected onto $(v,s)$-space. c The three-dimensional system from a different angle. Note the initial approach of the trajectory onto the critical manifold. d The corresponding system projected onto $(v,w)$-space. Note, this view provides a clear delineation between the singular canard and singular trajectories while the others do not. Hereafter, this projection is used when comparing canards and their respective trajectories