Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Nov 11;3:3176. doi: 10.1038/srep03176

Morphing Surfaces Enable Acoustophoretic Contactless Transport of Ultrahigh-Density Matter in Air

Daniele Foresti 1, Giorgio Sambatakakis 1, Simone Bottan 1, Dimos Poulikakos 1,a
PMCID: PMC3822381  PMID: 24212104

Abstract

The controlled contactless transport of heavy drops and particles in air is of fundamental interest and has significant application potential. Acoustic forces do not rely on special material properties, but their utility in transporting heavy matter in air has been restricted by low power and poor controllability. Here we present a new concept of acoustophoresis, based on the morphing of a deformable reflector, which exploits the low reaction forces and low relaxation time of a liquid with enhanced surface tension through the use of thin overlaid membrane. An acoustically induced, mobile deformation (dimple) on the reflector surface enhances the acoustic field emitted by a line of discretized emitters and enables the countinuos motion of heavy levitated samples. With such interplay of emitters and reflecting soft-structure, a 5 mm steel sphere (0.5 grams) was contactlessly transported in air solely by acoustophoresis.

Transport of solids and liquids at small scale has always been a difficult challenge, since adhesion forces play a major role at mm sizes and below1. Particularly at small scales, impurity, contamination and surface forces hamper the integrity of the sample when droplets and particles are in contact with a solid surface. A successful objective in the past years has been the engineering of solid surfaces to reduce frictional losses, establishing new fields such as superhydrophobicity2,3,4, and even further by modifying the droplet surface itself5. However, these approaches still require contacts (i.e. they are hampered by possible contamination issues) and the motion of the sample is subjected to material property dependencies such as electrostatic6, electromagnetic and optical properties7,8,9, also often requiring preliminary processing of the sample5 or of the carrying medium10.

Acoustic radiation forces have been successfully used in lab-on-chip applications for the handling of microparticles in liquid solutions11. The term acoustophoresis12 is employed to describe related motion of matter, ranging from the simple changes in particle concentration13 and handling14 to the bidimensional transport of single worms15. However, the exploitation of acoustophoresis in air is intrinsically much more challenging. Much like a human can easily swim in water but cannot fly in air, the negligible contribution of buoyancy forces in a hosting gas medium compared to a liquid magnifies the challenge of acoustic transport in air. In fact, although the first transport of a particle in a liquid through the use of acoustophoreris dates back almost 40 years16, controlled acoustophoresis in air has been only very recently experimentally demonstrated17.

Enhancing the magnitude and the stability of such forces would extend their applicability to very high density materials, i.e. most metals and alloys. Near-field acoustic levitation has been shown to move contactlessly high density material such as glass or metal, but the technique is limited to flat, solid samples18. In conventional acoustic levitation in air, a particle is trapped at a node of an axisymmetric levitator, with no possibility of motion. In such systems the shape of the reflector and emitter are key factors, since their mutual interaction can enhance the acoustic field by several orders of magnitude19. Therefore, the levitator geometry has been the subject of numerous studies, including the focusing and stabilizing effect20 that a reflector curvature can have on the sample trapping. Such force enhancement increased the position stability of the levitated object and allows for a wide range of sample analysis21. However, such levitator geometries are fixed in space and at most can levitate heavy objects at a fixed position.

Soft reflectors have been used with the intent to increase levitation power22. By increasing the acoustic power, the radiation pressure is sufficient to deform the surface of liquids and soft materials22. The deformation changes in turn the acoustic resonance frequency of the acoustic levitator, modifying the acoustic field: the steady-state nature of the radiation pressure couples with the reaction forces of the reflecting material. The first application of this phenomenon to trap heavy samples in an axisymmetric levitator has been qualitatively reported by Hong et al23.

Acoustophoresis in air and the resulting planar transport have a weak focusing effect due to the flat nature of the reflecting surface. When dealing with a heavy material (density ρ > 0.5 g/cm3), the motion is characterized by sample oscillations at the potential nodes, due to the low damping effect offered by the hosting medium (i.e. air). A reduction of these oscillations would be possible by a geometry that would focus the acoustic waves, strengthening the restoring forces20. Any permanent curvature of the reflector would be beneficial to the restoring forces in two (axisymmetric19) or one (line focused24) directions, but the permanency of the curvature would at the same time prohibitively restrict free planar transport, of the kind demonstrated recently with a flat reflector17.

This paper presents a concept that exploits the acoustic morphing ability of the surface of an engineered material made of a plastic wrap membrane stretched on the surface of a liquid of optimized properties, to enable morphing through acoustic radiation pressure, a key factor for acoustophoretic contactless handling of high density materials. By adapting itself locally at the needed location, it focuses the acoustic field (both restoring force components) and enhances the magnitude of the levitation force. The surface deformation assumes a concave shape, which moves along with the levitation node and the transported sample, creating a spatially and temporally optimized deformation. Such concave areas move at the speed of the transported sample. To showcase the potential and functionality of the system, a steel sphere of 5 mm in diameter (mass of 0.5 g) was acoustophoretically transported along a 16 mm path.

In addition, the physics of the acoustic and reactive forces of the material deformation was studied through a three dimensional numerical model. The acoustic force depends on the morphed geometry, and vice versa. The material structure (polypropylene membrane on a glycerin surface) was experimentally studied and shown to behave linearly in a wide range of elasticity. The coupled acoustic-structural model was validated by means of a line-focused acoustic levitator, and the results were comparable to the experiments.

Results

A typical acoustic levitation device is composed by an emitter and a reflector placed at a distance H. By vibration of the emitter, an intense acoustic field can be created, strong enough to levitate an object under terrestrial gravity conditions. The acoustic field exerts a mean radiation pressure:

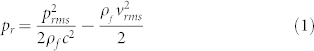graphic file with name srep03176-m1.jpg

where prms and vrms are the root mean square acoustic pressure and velocity, respectively, and ρf and c are the density and the speed of sound of the acoustic medium, respectively.

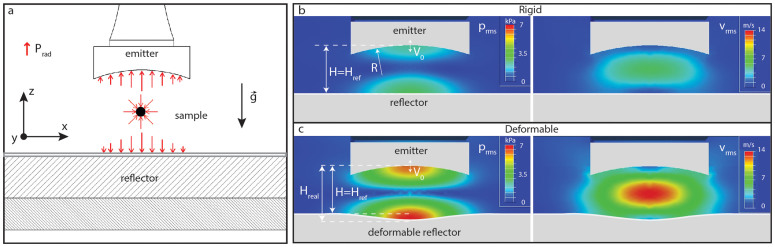
The radiation pressure of Eq. (1) results in a net force when integrated on the surfaces of emitter, reflector and sample (Fig. 1a). To achieve the highest force24, the emitter is placed at a resonance distance H ≈ λ/2, from the reflector where λ is the acoustic wavelength, to establish a standing wave with a single vertical acoustic node where the sample is placed (Fig. 1b). If soft-enough it is possible in principle to have the reflector deform under the effect of the radiation pressure (Fig. 1c). For a constant emitter oscillation frequency f and velocity amplitude V0, both acoustic pressure and particle velocity depend on the levitator geometry. By varying the height H in the proximity of λ/2, the resonant height Hr of the levitator is found, corresponding to the strongest acoustic field. Hr also depends on many other geometrical parameters19,24, with the most influencing factor being the curvature of the reflector.

Figure 1.

Figure 1

Open in a new tab

(a) A line-focused acoustic levitator, front view. The radiation pressure acts on the emitter, reflector and levitated sample. (b) Rigid configuration of a line-focused levitator, front view, along with the acoustic prms and vrms distributions. (c) A deformable reflector morphs under the radiation pressure effect, enhancing the acoustic field. The velocity V0 is the same of the rigid case, and in this specific configuration the acoustic pressure and velocity increases by a factor 2 by the sole morphing of the soft reflector.

To study the enhancement of the force acting on small levitating particle, it is of convenience to introduce the Gor'kov's force potential 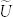Inline graphic25:

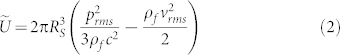graphic file with name srep03176-m2.jpg

In Eq. 2, the particle size is considered to be much smaller than the acoustic wavelength λ [effectively, Rs/λ < 0.126]. The potential in equation (2) is valid under the assumption of density of the sample ρs much larger then ρf and its compressibility βs much smaller than the one of the surrounding fluid βf (for a water droplet levitated in air, ρs/ρf ~ 103 and βs/βf ~ 7·10−5). Its non-dimensional form is:

graphic file with name srep03176-m3.jpg

The levitation force acting on a small sphere can be predicted by:

graphic file with name srep03176-m4.jpg

The subscript i identify the x, y and z directions. The focusing effect of the soft reflector enhances the acoustic potential in both the vertical (z) and horizontal components (x and y, Fig. 1a). The vertical component Fz is directly responsible for levitation, and the sample of mass m = 4/3 π Rs3ρs is levitated at the position z for which Fz − mg = 0. The horizontal components, Fx and Fy, are responsible for the centering of the sample at the levitation node: an increase of the horizontal force components improves the stability of the sample levitation and transport, reducing the oscillation of the sample around the levitation node. This improvement has benefits on the maximum actual vertical force as well, since the density of the sample that can be levitated is increased27,28.

Fig. 1c shows the novel levitator configuration of present study, in which the reflector deforms to a typical concave shape due to the acoustic field itself. As a result of deformation, the acoustic field is increased in magnitude compared to the flat configuration, and a higher force is applied by the radiation pressure on the deformable surface. The geometry self-adapts again until a final equilibrium is found. For an axisymmetric rigid reflector, the enhancement of the levitation potential has optimal values of curvature in the range R = 1 ÷ 2 λ24,29,30. Such curvatures require a deformation of the present soft self-focusing structure in the mm range for an operating frequency of 25 kHz. Considering the radiation pressure of interest pr to be 10 ÷ 100 Pa, the soft reflector should be characterized by a Young's modulus E in the range 0.1 ÷ 1 kPa. Preliminary tests with polydimethylsiloxane (PDMS) showed strong limitations due to insufficient crosslink at very low Young's modulus (below 1 kPa, Supplementary Movie S1), which led to a jelly-like and adhesive reflector. The use of hydrogels is limited by the inherent dependence of mechanical properties on their hydration state, temperature and stress, which lead to alteration of the material response after long term use31. The time scale of the acoustophoretic transport (0.1–1 second) is an additional limitation for these materials, since their relaxation time is high, of the order of seconds32. As a result, the concavity cannot promptly recover and follow to the planar motion of the levitation node, prohibiting contactless transport of matter.

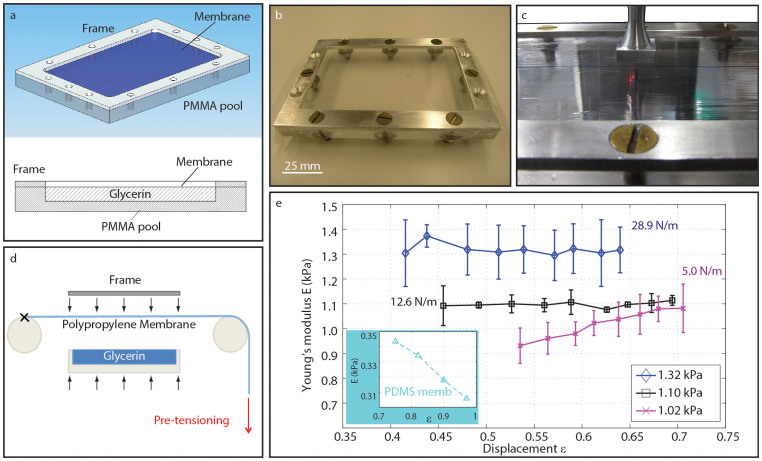
To design an acoustically morphing surface according to the requirements explained above, a tank was filled with glycerin and covered with a polypropylene membrane as shown in Fig. 2a. The polypropylene membrane (commercially available food packaging cellophane) had an estimated thickness of 7.5 μm. The liquid tank was a 135 × 100 × 7 mm Poly(methyl methacrylate) (PMMA) container. This length and width minimized the effect of the edges of the acoustic field on the levitation sites and provided sufficient travel length for transport. The depth guaranteed a deformation sufficient for the acoustic requirements, without interfering with the bottom of the solid pool. The highly pure glycerine had a density of 1.26 g/cm3 and viscosity of ~1.4 Pa·s (Fig. 2b). All materials were purposely chosen to be transparent to light, so that optical access was guaranteed for laser vibrometer measurements (Fig. 2c).

Figure 2. The reflector structure.

Figure 2

Open in a new tab

(a) Isometric and lateral views. (b) One of the manufactured components (frame) before its use in the reflector device (c) The transparency of polypropylene, glycerin and water allowed laser vibrometer measurements directly during the drop-test experiments. (d) The structure assembly. Pre-tensioning allows the calibration of the final stiffness. (e) Indentation test for three different pre-tensioning values after applying the Dimitriadis model33. The pre-tensioning is measured in N/m as applied tension per unit of width of membrane. The displacement ε is normalized based on the reflector liquid thickness. Young's modulus values: Pretensioning 5 N/m, 1.02 ± 0.07 kPa; 12.6 N/m, 1.10 ± 0.03 kPa; 28.9 N/m, 1.3 ± 0.1 kPa. For smaller Young's modulus, a PDMS membrane was used instead of cellophane. The indentation test showed a strong nonlinearity, and an estimate average Young's modulus of 0.34 kPa. A deformation of 0.7 was already reached for the lowest load of the indentation test.

Such a structure is required in light of the complex interaction of the acoustic waves with liquid and membrane. It is worth mentioning that using only a liquid in direct contact with the acoustic field is not possible due to the high acoustic power. When this was done, the acoustic radiation pressure focused on a point, destroying the continuity of the liquid surface and trapping macro-bubbles (Supplementary Movies S2, S3). Employing solely a membrane requires high pre-tensioning to achieve a flat surface. Such pre-tensioning increases the final stiffness of the structure, which becomes too rigid to morph in response to the acoustic field. The employed hybrid liquid/membrane system combines the advantages of its individual components. The surface liquid keeps the membrane flat, while the membrane prevents bubble formation in the liquid. Moreover, the membrane provides a protection layer to the liquid from the environment. The size of the entire structure is defined by the size of solid tank. The use of a high viscosity liquid (glycerin) helped reduce undesired effects of the acoustic field (i.e. rippling) on the liquid surface. In fact, using water or a liquid with low viscosity to reduced the stability of the levitation, since surface waves may occur at the driving frequency even in presence of the membrane (Supplementary Movie S4). The flexibility of the liquid/membrane concept allows elasticity calibration of the structure by simply pre-tensioning the membrane (Fig. 2d). For the employed values (E = 0.5–1 kPa), the aggregate structure can be approximated as a linear material (Fig. 2e).

To assemble the structure and to calibrate the desired elasticity, an in-house apparatus was designed and realised (Fig. 2d).

The stiffness of the polypropylene membrane did not permit to manufacture a composite structure with a Young's modulus below 1 kPa. By fabricating the reflector with a thin layer (200–300 μm) of PDMS (E ≈ 10–20 kPa), an equivalent Young's modulus of 0.3–0.4 kPa was reached. The indentation results (Fig. 2e) show how the limit of the linearity assumption is already evident for the softest polypropylene reflector (E = 1.02 kPa), and the PDMS membrane reflector is well beyond this limit (Fig. 2e, blue box). For this sample, the Young's modulus is evaluated to be in the range 0.3–0.35 kPa for deformation in the range 0.9–0.7.

In order to demonstrate the capability of the morphing reflector concept for acoustic levitation and transport, the self-focusing reflector was employed for acoustophoresis of a steel ball. A line of five piezoelectric transducers was used for such purpose17 (Fig. 3a). The acoustophoretic method is based on the spatiotemporal modulation of the acoustic levitation potential within the acoustic chamber. Figure 3b showcases how the induced local self-focusing effect make possible the controlled contactless transport of a steel spheres of 5 mm of diameter (density ρs = 7.9 g/cm3, total mass = 0.5 g) along a 16 mm path solely by acoustophoretic forces. The acoustically induced dimple moves along with the sample and the acoustic node. Acoustophoretic contactless transport of a 2 mm steel sphere (total mass = 32 mg) along a path of several cm is shown in Supplementary Movie S6.

Figure 3. Acoustophoretic handling of heavy matter in air.

Figure 3

Open in a new tab

(a) The acoustophoretic set-up and its function. The emitters are Langevin piezo transducers (LPTs) used as acoustic sources. The driving voltage is varied within time t between two adjacent LPT (A1 and A2) with a maximum value of A0 (120 Volts). This modulation allows the smooth motion of the acoustic node during a period T, time needed to move the acoustic node between two adjacent emitters. (b) Contactless transport of a steel ball. The sphere size is 5 mm in diameter and travels between two neighboring emitters. The dimple on the morphing reflector travels along with the acoustic field and the sample. For this experiment, a PDMS membrane was used.

In order to study and quantify the physics of the acoustic-reaction force interaction with the deformable surface, a numerical model was developed, to determine the acoustic field in the levitator, including the modeling of the reflector deformation due to the acoustic forces. The corresponding acoustic field variation due to geometrical changes is computed and the process is iterated until convergence is obtained (Supplementary Movie S5). The numerical results were compared with a study case of a line-focused levitator24 (Fig. 1a, Methods).

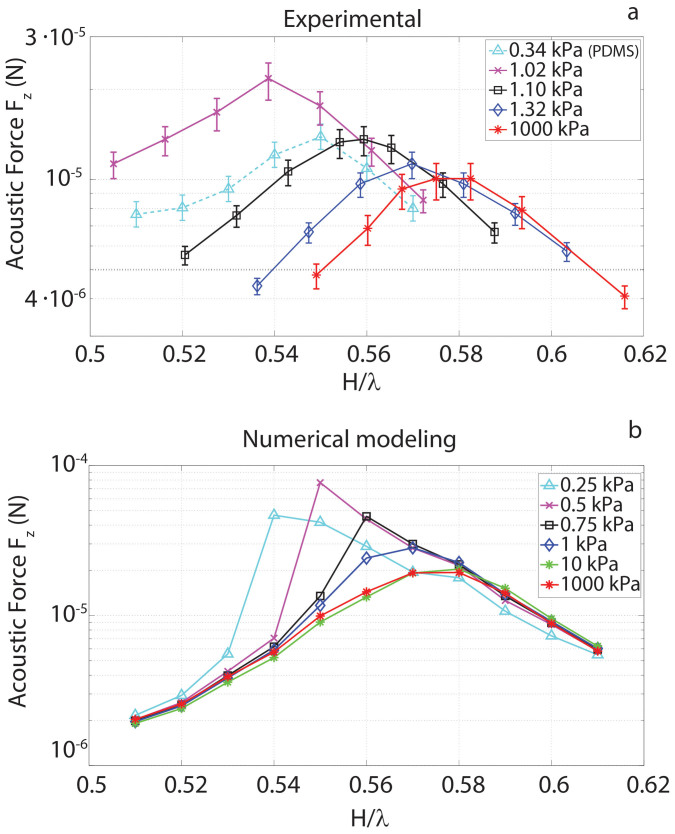
The experimental results of the acoustic forces acting on a spherical particle as a function of the reflector height H, for different soft reflector Young's moduli, E, is shown in Fig. 4a. The typical dome-shaped resonance curves are present for all the reflectors.

Figure 4.

Figure 4

Open in a new tab

(a) Experimental results. The heights are scanned from high to low. The drop-test was reproducible, and the error bars are calculated based on the uncertainty on the velocity measurements by laser vibrometer (V0 = V ± 0.05 m/s). (b) Numerical acoustic vertical force acting on a sphere (ρ = 2.2 g/cm3, Rs = 0.5 mm). The resonant height shift toward lower values for softer reflectors. The acoustic power increases until a peak at E = 0.5 kPa is reached. Subsequently it decreases confirming the qualitative behavior of the experimental investigation.

At lower E, an enhancement of the levitation forces takes place: the dimple produced on the reflector surface by the radiation pressure has a focusing effect on the field, increasing the force acting on a particle introduced inside of the levitator (higher levitation forces and horizontal stability). The acoustic force magnitude is enhanced up to 120% compared to the rigid flat surface case (reflector of E = 1.02 kPa). This behavior is not monotonic. To this end, if a moderate deformation enhances the field, an excessive deformation reduces it.

The resonant height shift Hr shows also a non-monotonic behaviour: by decreasing the elastic modulus of the reflector a higher deformation is obtained until a minimum height of H = 0.54 λ for E = 1.02 kPa is reached. For the softest reflector with the PDMS membrane the resonance height increases again until H = 0.55 λ. The considered distance H in this analysis is a reference height measured in the undeformed, initial configuration Href (Fig. 1b), while the real distance in the final configuration is higher, Hreal. As a consequence, the more the reflector is deformable, the sooner the resonance height is reached (Fig. 1c). In this case, a softer reflector corresponds to an increase of the real resonant height. This behavior is typical in acoustic levitators19,24,30: strong emitter/reflector curvatures are usually characterized by higher resonance heights than the plane wave ideal case of H = 0.5 λ. On the other hand, if the deformation spreads over a large area of the deformable reflector, as for the PDMS membrane reflector, its curvature radius increases, requiring a lower reflector height (approaching the plane reflector case).

The experimental results show a good qualitative agreement with the numerical model (Fig. 4b). The increase in the vertical force magnitude has its peak for E = 0.5 kPa. This corresponds to an enhancement of 320% compared to the case of a flat rigid reflector (E > 10 kPa). The deformation of the reflector strongly increases the acoustic force magnitude within the cavity, but affects only slightly the overll pattern of the acoustic field compared to the undeformed case (maximum deformations of the reflector are in the order of 0.1 H, Figs. 1b–c). From Eq. (4), an equivalent enhancement of the restoring force in the x and y directions is expected. The difference in magnitude between numerical model and experiment is mainly due to the force measurement method (Supplementary Fig. S1), with the drop test underestimating the force by about 50%. Additionally, it is worth noting that while in the simulations the vibrational velocity V0 was fixed to V0 = 1 m/s, in the experiments V0 was varied controlling the driving voltage of the emitter. The Vmin was then normalized with respect to V0 to calculate the equivalent force, but this scaling cannot be performed for the displacement of the reflector. Indeed, the deformation itself depends on the actual force magnitude. Vmin in the experiments was close to 1 m/s for the peak force, reducing the disagreement. The difference increased by moving off the peak, since Vmin far exceeds V0. A wider profile would be expected for the same boundary condition, better matching the experiment. In addition, an error of 150 μm in height is expected, due to the practical difficulty of having a perfectly parallel position between the emitter and the reflector structure.

The resonant height also shifts toward lower values for softer reflectors, but in contrast to the experiments this behavior is monotonic. We believe this is due to the nonlinear nature of the very soft reflector, already coming to play for a Young's modulus of E = 1.02 kPa (Fig. 2e). For such a soft reflector, a more detailed model is needed. Indeed, the contribution of the surface tension and the hydrostatic load of the liquid layer play an important role for low tension of the membrane23.

Discussion

A morphing, soft-reflector concept, enabling acoustophoretic contactless transport of high-density objects in air, has been introduced and investigated experimentally and numerically. A composite membrane-liquid (polypropylene, glycerin) surface material has been designed and experimentally characterized for this purpose. Its linear behavior has been confirmed for Young moduli as low as 1 kPa. The acoustically induced local deformation and its controlled variation and planar motion in space and time, has enabled the acoustophoretic contactless transport of a steel sphere of 5 mm in diameter (0.5 grams) in air. The acoustic field coupling and enhancement has been experimentally and numerically studied. The results showed an increasing of the levitation power to more than 120% for a 1.02 kPa reflector.

This study extends the potential of acoustic transport of levitated heavy material, addressing the importance of acoustically morphing reflector surfaces. Such an advancement significantly extends the range of application of acoustic levitation beyond stationary trapping.

Methods

The model

The three-dimensional finite element model was developed using Simulia Abaqus 6–11. The model is composed of two modules, linear acoustic and static deformation: the former calculates the acoustic field within the line-focused levitator; the latter calculates the deformation of the reflector under a specified load. Both models allow very large deformations. In particular, the reflector allows deformation up to 80% of its thickness, with the acoustic medium adapting accordingly (Supplementary Movie S5). The two models were interfaced iteratively through an in-house developed Python code. Using the value of acoustic pressure and velocity calculated by the first module, the code computes the acoustic radiation pressure load using Eq. 1. The two modules iterate until a final equilibrium criterion is satisfied. The applicability of such acoustic modeling to study acoustic forces has been already demonstrated, and the FEM model has been experimentally validated26.

The line-focused levitator

The line-focused levitator is composed by an emitter, a radiating plate of a Langevin Piezo Transducer LPT with square cross-section (15 × 15 mm), and a reflector, our composite membrane-glycerene structure. A curvature of R = 21 mm enhanced the levitation along one orthogonal direction. A wave generator and an amplifier (ECLER DPA-4000T) were employed to drive the LPT with a sinusoidal signal of frequency f = 25.8 kHz and voltage amplitude A = 0–120 V.

The morphing reflector

To assemble the morphing reflector and to calibrate the desired elasticity an in-house apparatus has been designed and realised (Fig. 2f). The polypropylene layer is held between two cylinders, with one edge constrained and the other free to translate. On the unconstrained side a known tension is applied. At the desired tension, the tank containing the glycerin is approached underneath the layer. The membrane adheres to the liquid due to the surface tension. A small tilt avoids air bubble trapping. In a last step, an aluminium frame is placed on top of the reflector edges and bolted at eight anchoring points. The procedure is simple and easily reproducible. Three pre-tensioning levels were used. A pre-tensioning of 5 N/m was selected to realize a high deformability reflector, and at the same time to avoid the formation of ripples along the membrane surface which would appear for lower values of pre-tensioning. Pre-tensioning of 28.9 N/m represented the high limit, still allowing a moderate deformability under the acoustic field forces. An intermediate pre-tensioning of 12.6 N/m was also used. The reproducibility of the prescribed method is good: three reflector shapes for each different membrane tension were produced (a total of nine reflectors), and the measured Young's modulus variation was ±8% (E = 1.3 ± 0.1 kPa, 1.10 ± 0.03 kPa and 1.02 ± 0.07 kPa, Fig. 2e).

The indentation test

The indentation test on the device was performed with an in-house set-up. The low Young's modulus required a very soft load cell, rendered in our case by a discretized column of known weights acting above a 7 mm diameter steel sphere in contact with the center of the reflector. By reconstructing the deformation through image processing (Image J ver. 1.46), the displacement for each weight was obtained. The displacement-stress relationship is finally computed with the Dimitriadis model33.

Drop test

The force acting on the particle was measured by means of the drop test27,28. In a drop test, the particle is placed at the levitation site at high acoustic levitation power. By decreasing the driving voltage A, V0 was also decreased. V0 was measured by means of a laser vibrometer (Polytec CLV-2534). Vmin is the minimum value of V0 allowing levitation at a certain height H. By using Eqs. (2–4) and normalizing the force to V0 = 1 m/s, the force can be compared to the numerical model24. The particles used for the drop tests were spheres of polystyrene (1 g/cm3), glass (2.2 g/cm3), alumina (3.2 g/cm3) and ceramic (4 g/cm3). In order to minimize the interference with the acoustic field, the radius Rs for all the spheres was 0.5 mm (Rs < 0.1 λ ~ 0.7 mm suffices26). The drop-test is a very simple and non-invasive method. On the other hand this test has been shown to underestimate the force magnitude of 30–50%26,27,28. The validation performed for the present set-up shows similar limitations (Supplementary Fig. S1).

Author Contributions

D.F. and D.P. designed the research. G.S. and D.F. performed the experiments and developed the numerical model. S.B. contributed to the material characterization. D.F. and D.P. wrote the paper. All the authors proofread the paper.

Supplementary Material

Supplementary Information

Supplementary Information

srep03176-s1.doc (1.1MB, doc)
Supplementary Information

Supplementary Movie 1

Download video file (995.5KB, mov)
Supplementary Information

Supplementary Movie 2

Download video file (551.4KB, mov)
Supplementary Information

Supplementary Movie 3

Download video file (502.5KB, mov)
Supplementary Information

Supplementary Movie 4

Download video file (507.8KB, mov)
Supplementary Information

Supplementary Movie 5

Download video file (3.5MB, mov)
Supplementary Information

Supplementary Movie 6

Download video file (2MB, mov)

Acknowledgments

Funding for this work provided by the Swiss National Science Foundation (SNF), grant No. 144397 is gratefully acknowledged. We thank Bruno Kramer, IPE-ETH Zurich, for manufacturing of parts of the devices and Carlo Antonini and Thomas Vasileiou, LTNT-ETH Zurich, for helpful discussions.

References

  1. Quere D. Wetting and roughness. Annu Rev Mater Res 38, 71–99 (2008). [Google Scholar]
  2. Tuteja A., Choi W., Mabry J. M., McKinley G. H. & Cohen R. E. Robust omniphobic surfaces. P Natl Acad Sci USA 105, 18200–18205 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Zheng Y. M., Gao X. F. & Jiang L. Directional adhesion of superhydrophobic butterfly wings. Soft Matter 3, 178–182 (2007). [DOI] [PubMed] [Google Scholar]
  4. Bhushan B., Koch K. & Jung Y. C. Nanostructures for superhydrophobicity and low adhesion. Soft Matter 4, 1799–1804 (2008). [Google Scholar]
  5. Aussillous P. & Quere D. Liquid marbles. Nature 411, 924–927 (2001). [DOI] [PubMed] [Google Scholar]
  6. Cho S. K., Moon H. J. & Kim C. J. Creating, transporting, cutting, and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits. J Microelectromech S 12, 70–80 (2003). [Google Scholar]
  7. Smalyukh I. I., Kachynski A. V., Kuzmin A. N. & Prasad P. N. Laser trapping in anisotropic fluids and polarization-control led particle dynamics. P Natl Acad Sci USA 103, 18048–18053 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Kauffmann P. et al. Contactless Dielectrophoretic Handling of Diamagnetic Levitating Water Droplets in Air. Ieee T Magn 46, 3293–3296 (2010). [Google Scholar]
  9. Ilievski F., Mirica K. A., Ellerbee A. K. & Whitesides G. M. Templated self-assembly in three dimensions using magnetic levitation. Soft Matter 7, 9113–9118 (2011). [Google Scholar]
  10. Kose A. R., Fischer B., Mao L. & Koser H. Label-free cellular manipulation and sorting via biocompatible ferrofluids. P Natl Acad Sci USA 106, 21478–21483 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Kozuka T., Tuziuti T., Mitome H. & Fukuda T. Control of a standing wave field using a line-focused transducer for two-dimensional manipulation of particles. Jpn J Appl Phys 1 37, 2974–2978 (1998). [Google Scholar]
  12. Yu G., Chen X. L. & Xu J. Acoustophoresis in variously shaped liquid droplets. Soft Matter 7, 10063–10069 (2011). [Google Scholar]
  13. Nordin M. & Laurell T. Two-hundredfold volume concentration of dilute cell and particle suspensions using chip integrated multistage acoustophoresis. Lab on a Chip 12, 4610–4616 (2012). [DOI] [PubMed] [Google Scholar]
  14. Dual J. et al. Acoustofluidics 19: Ultrasonic microrobotics in cavities: devices and numerical simulation. Lab on a Chip, 4010–4021 (2012). [DOI] [PubMed] [Google Scholar]
  15. Ding X. Y. et al. On-chip manipulation of single microparticles, cells, and organisms using surface acoustic waves. P Natl Acad Sci USA 109, 11105–11109 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Dyson M., Woodward B. & Pond J. B. Flow of Red Blood Cells Stopped by Ultrasound. Nature 232, 572–573 (1971). [DOI] [PubMed] [Google Scholar]
  17. Foresti D., Nabavi M., Klingauf M., Ferrari A. & Poulikakos D. Acoustophoretic contactless transport and handling of matter in air. P Natl Acad Sci USA, 10.1073/pnas.1301860110 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ueha S., Hashimoto Y. & Koike Y. Non-contact transportation using near-field acoustic levitation. Ultrasonics 38, 26–32 (2000). [DOI] [PubMed] [Google Scholar]
  19. Xie W. J. & Wei B. Dependence of acoustic levitation capabilities on geometric parameters. Phys Rev E 66, 026605 (2002). [DOI] [PubMed] [Google Scholar]
  20. Baer S. et al. Analysis of the particle stability in a new designed ultrasonic levitation device. Review of Scientific Instruments 82, 105111 (2011). [DOI] [PubMed] [Google Scholar]
  21. Welter E. & Neidhart B. Acoustically levitated droplets - A new tool for micro and trace analysis. Fresen J Anal Chem 357, 345–350 (1997). [Google Scholar]
  22. Hong Z. Y., Xie W. J. & Wei B. Interaction of acoustic levitation field with liquid reflecting surface. Journal of Applied Physics 107, 014901 (2010). [Google Scholar]
  23. Hong Z. Y., Xie W. J. & Wei B. Acoustic levitation with self-adaptive flexible reflectors. Review of Scientific Instruments 82, 074904 (2011). [DOI] [PubMed] [Google Scholar]
  24. Foresti D., Bjelobrk N., Nabavi M. & Poulikakos D. Investigation of a line-focused acoustic levitation for contactless transport of particles. Journal of Applied Physics 109, 093503 (2011). [Google Scholar]
  25. Barmatz M. & Collas P. Acoustic Radiation Potential on a Sphere in Plane, Cylindrical, and Spherical Standing Wave Fields. J Acoust Soc Am 77, 928–945 (1985). [DOI] [PubMed] [Google Scholar]
  26. Foresti D., Nabavi M. & Poulikakos D. On the Acoustic Levitation Stability Behavior of Spherical and Ellipsoidal Particles. Journal of Fluid Mechanics 709, 581 (2012). [Google Scholar]
  27. Vandaele V., Delchambre A. & Lambert P. Acoustic wave levitation: Handling of components. Journal of Applied Physics 109, 124901 (2011). [Google Scholar]
  28. Vandaele V. Contactless handling for micro-assembly: acoustic levitation, Université libre de Brixelles, (2011). [Google Scholar]
  29. Xie W. J., Cao C. D., Lu Y. J. & Wei B. Levitation of iridium and liquid mercury by ultrasound. Physical Review Letters 89, 104304 (2002). [DOI] [PubMed] [Google Scholar]
  30. Andrade M. A. B., Buiochi F. & Adamowski J. C. Finite Element Analysis and Optimization of a Single-Axis Acoustic Levitator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 57, 469–479 (2010). [DOI] [PubMed] [Google Scholar]
  31. Ottenbrite R. M., Park K. & Okano T. Biomedical Applications of Hydrogels Handbook. [Google Scholar]
  32. Mao R., Tang J. & Swanson B. G. Relaxation time spectrum of hydrogels by CONTIN analysis. J Food Sci 65, 374–381 (2000). [Google Scholar]
  33. Dimitriadis E. K., Horkay F., Maresca J., Kachar B. & Chadwick R. S. Determination of elastic moduli of thin layers of soft material using the atomic force microscope. Biophys J 82, 2798–2810 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep03176-s1.doc (1.1MB, doc)
Supplementary Information

Supplementary Movie 1

Download video file (995.5KB, mov)
Supplementary Information

Supplementary Movie 2

Download video file (551.4KB, mov)
Supplementary Information

Supplementary Movie 3

Download video file (502.5KB, mov)
Supplementary Information

Supplementary Movie 4

Download video file (507.8KB, mov)
Supplementary Information

Supplementary Movie 5

Download video file (3.5MB, mov)
Supplementary Information

Supplementary Movie 6

Download video file (2MB, mov)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES