Figure 1.

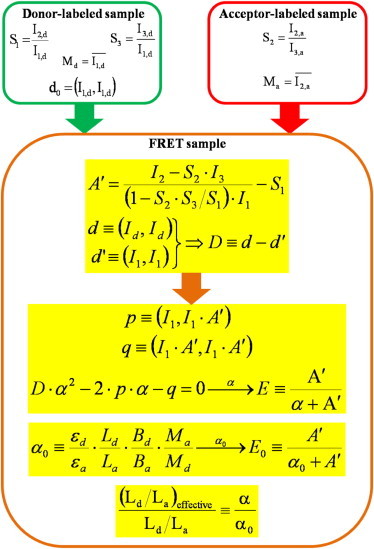
Flow-chart and summary of the main formulae for determining FRET based on intensity correlations. As the starting point, single donor-only labeled samples are analyzed for determining the S₁, S₃ spectral spillage factors, the M_d intensity mean, and the d₀ intensity variance, then single acceptor-labeled samples are analyzed for determining the S₂ spectral spillage factor and the M_a intensity mean. In the knowledge of S₁, S₂, and S₃, the FRET-related quantity A′ is determined based on the double-labeled FRET sample: A′ is a single-valued, monotonously increasing function of the transfer efficiency E for the accurate calculation of which a scaling of A′ with the scaling factor α is necessary. After scaling of A′ with α, FRET efficiency E is calculated as E = A′/(α + A′), with the meaning A′/α = (R₀/R)⁶ (from Förster’s formula). Calculation of covariance-based α begins with determination of D, the difference between the variance of the hypothetical (immeasurable, indirectly determined) donor intensity when FRET is switched off (d), and the variance of donor intensity (measurable) when FRET is switched on (d′), both characterizing the double-labeled FRET sample. In the absence of any steric interaction between the dye-targeting labels (e.g., no competition) instead of d, the d₀ variance of the donor-only sample can be used for calculation of D. In the presence of steric influence, the functional dependence of the change in the intensity variance (Q′) on the change in mean intensity (Q) characterized with the m slope and b intercept parameters (Q′ = m · Q + b) can be used for estimating d and D on the FRET sample in the knowledge of d′, A′, and α. It can be noted that whereas in the former case D does not depend on α, in the latter case it does, with the consequence that a cubic equation should be used for α, instead of a quadratic one (see below). After determining D (or expressing it as the function of α), coefficients of p and q are calculated with I₁, and A′ on the double-labeled sample. In the knowledge of D, p, and q, a quadratic (or more complicated, depending on the nature of D, see also the Supporting Material) equation is solved for α. The fact that the D, p, and q coefficients are population averages of fluctuation (deviation from the mean) products implies two alternatives for solution of the equation for α: either it can be solved for α for each individual cell, i.e., on a cell-by-cell basis and histograms of α are created from which some characteristic expressing average behavior (mean, mode, median) is calculated (followed when D is independent of α); or the averages of the appropriate fluctuation product histograms (cell-by-cell distributions of D, p, q) are calculated first, then the equation is solved for an average α (followed when D depends on α). Finally, E is calculated with α and A′ on a cell-by-cell basis. The α-factor in the conventional way is determined from the relative absorption, labeling ratio, receptor number, and intensity (spectral α or α₀). FRET efficiency of E₀ is calculated with α₀ and A′ on a cell-by-cell basis. By taking a ratio, α/α₀ = (L_d/L_a)_effective can be introduced, expressing the reduction in quantum yield or binding efficiency of the fluorescently labeled ligand as the function of the degree of labeling of ligands.