Abstract
The kidney uses mixtures of five osmolytes to counter the stress induced by high urea and NaCl concentrations. The individual roles of most of the osmolytes are unclear, and three of the five have not yet been thermodynamically characterized. Here, we report partial molar volumes and activity coefficients of glycerophosphocholine (GPC), taurine, and myo-inositol. We derive their solvation behavior from the experimental data using Kirkwood-Buff theory. We also provide their solubility data, including solubility data for scyllo-inositol. It turns out that renal osmolytes fall into three distinct classes with respect to their solvation. Trimethyl-amines (GPC and glycine-betaine) are characterized by strong hard-sphere-like self-exclusion; urea, taurine, and myo-inositol have a tendency toward self-association; sorbitol and most other nonrenal osmolytes have a relatively constant, intermediate solvation that has components of both exclusion and association. The data presented here show that renal osmolytes are quite diverse with respect to their solvation patterns, and they can be further differentiated based on observations from experiments examining their effect on macromolecules. It is expected, based on the available surface groups, that each renal osmolyte has distinct effects on various classes of biomolecules. This likely allows the kidney to use specific combinations of osmolytes independently to fine-tune the chemical activities of several types of molecules.
Introduction
The mammalian kidney uses a cocktail of several osmolytes to counteract the deleterious effects of the high renal urea and salt concentrations (1). The primary osmolytes are glycine-betaine, myo-inositol, glycerophosphocholine (GPC), sorbitol (2), and taurine (3) (see Fig. 1). It has been suggested that imbalances in the composition of cellular osmolyte cocktails contribute to diabetic neuropathic complications (4). In a similar way, in the kidney, specific mixtures of osmolytes appear to be needed for each set of conditions as one moves from the low urea/NaCl conditions of the renal cortex toward the high levels of urea/NaCl in the medulla. It has been demonstrated that GPC is the primary agent protecting against high urea, and that the sum of all osmolytes balances out high NaCl concentrations (5). Although the individual functions of the other four osmolytes are unclear, their distribution strongly suggests that specific ratios of osmolyte concentrations are needed for proper renal function, as mentioned above. Most notably, the concentration of myo-inositol first increases and then decreases, whereas concentrations of the other osmolytes increase continuously as one moves from the renal cortex into the medulla (2).
Figure 1.
Renal osmolytes. Structures were drawn using Chimera (26). To see this figure in color, go online.
The question is, why are so many different osmolytes used in the kidney, and what are their individual purposes? Knowledge of the microscopic solvation behavior of the osmolytes in solution can give valuable insight into this question. Thus, we measure physical properties that allow us to derive solvation properties. There are several approaches to this task, of which we use the rigorous Kirkwood-Buff (KB) theory (6). The physical properties of solutions are symptomatic of the underlying microscopic solvation (6), and it is possible to derive the microscopic properties from measurements of volumetric and chemical activity data (7). Based on this connection, it may come as no surprise that there is a correlation between the macroscopic properties of protein-free binary osmolyte solutions and their impact on proteins. Molar activity coefficients and osmotic coefficients of protein stabilizers tend to be larger than unity, whereas they are smaller for denaturants (8,9). Beyond such macroscopic correlations, knowledge of the microscopic solvation patterns is a powerful tool for deriving mechanistic information about osmolyte action (10,11).
Capturing the energetic impact of small additives on other biomolecules requires knowledge of the solvation patterns not only at the contact surface between the different molecular species (12–21) but also in free solution (22). Here, we provide such information about the behavior of the three renal osmolytes that have not yet been quantified, viz. GPC, taurine, and myo-inositol.
What concentration range of osmolytes is of biological interest? The amount of osmolytes found in situ varies drastically, depending on factors such as the species (23), the tissue (2), the cell type (24), and the nutritional status (5). For example, urea concentration may reach 5.4 M in water-independent desert rodents, whereas up to 3 M is more normal for water-dependent rodents (23). Extremes found in tissue culture are 1.1 mol/kg for sorbitol, 0.7 mol/kg for inositol, 0.2 mol/kg for glycine-betaine, and 0.14 mol/kg for GPC (24). In rat kidneys, GPC concentrations of 120 mM have been found under normal conditions, and these are approximately doubled after dehydration (25). Physiologic osmolyte concentrations thus can be quite high, and covering a broad concentration range in this work is expedient.
Materials and Methods
Densimetry
Measuring the density of osmolyte solutions allows us to derive the partial molar volumes of the osmolytes, as well as their solubilities. The three osmolytes under investigation, myo-inositol (Sigma, St. Louis, MO), taurine (USB, Cleveland, OH), and GPC (Bachem, Bubendorf, Switzerland) were all of the highest purity available. In addition, we used scyllo-inositol (Tokyo Chemical Industry, Tokyo, Japan) for comparison with its isomer myo-inositol. Due to the low solubility, however, it was not practical to use scyllo-inositol for the vapor-pressure measurements. To remove any residual water, the osmolytes were dried at 60°C for at least 20 h. Solutions were prepared gravimetrically using an analytical balance (AT20, Mettler-Toledo, Columbus, OH) equipped with an antistatic device. The densities of the solutions were measured in a DMA 5000M density meter (Anton Paar, Graz, Austria), using automatic viscosity correction.
Solubilities were measured as described previously (27), but with temperature controlled to 0.1 K. Briefly, water was added to dry osmolyte to produce a series of increasing nominal molalities. Dissolution of osmolyte crystals in water was allowed to equilibrate completely at 25°C. After equilibration, all crystals dissolve if the total osmolyte concentration is below the solubility limit. Above this limit, residual crystals remain and the supernatant has a constant osmolyte concentration. Accordingly, a breakpoint in the slope of the supernatant’s density versus the total osmolyte molality (sum of dissolved and undissolved osmolyte) marks the solubility limit (see Fig. 2). Densities of the supernatant were measured at several time points during the equilibration to ensure that equilibration was complete. The viscosity of concentrated GPC is too high to allow for a straightforward determination of its solubility. For myo-inositol, the equilibration was slow for final concentrations close to the solubility limit, so that it was possible to measure the densities of supersaturated solutions (after temporary heating to 40–50oC). Thus, densities of saturated solutions were determined under conditions far above the solubility limit, where equilibration was reasonably fast (a few days or less).
Figure 2.
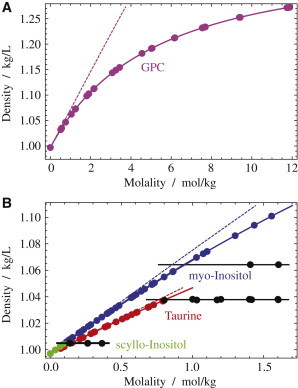
Densities of aqueous osmolytes at 25oC. Thin dashed lines represent density versus molarity. (A) Density for GPC. (B) Density for taurine and myo-inositol. Parameters of a fit to Eq. 1 are given in Table 1. Densities of saturated solutions (equilibrium supernatants over osmolyte crystals) are indicated in black. The solubilities of taurine and myo-inositol are 806 mmol/kg = 760 mM and 943 mmol/kg = 858 mM, respectively. Also shown is the density of scyllo-inositol solutions. The partial molar volume is 101 mL/mol, and the solubility is 101 mmol/kg = 99.7 mM. To see this figure in color, go online.
The partial molar volumes were obtained from the densities, as described previously (11). Using Wolfram Mathematica (Champaign, IL), the data were fit to a density equation that represents the ratio of the total mass of the solution per kilogram of water (numerator) to the total volume per kilogram of water (denominator). This approach is convenient for deriving the partial molar volume, because the partial molar volume and its derivatives are the only unknowns in the equation; they are in the denominator’s power series:
| (1) |
Here, is the molecular weight of the respective osmolyte, is the density of plain water, is the limiting partial molar volume of the osmolyte at 0 molal, and the other are derivatives with respect to the molality, m, of the osmolyte. The partial molar volume of the osmolyte is the first derivative of the volume (the denominator in Eq. 1) and is thus given by a power series that has its indices shifted by 1:
| (2) |
The partial molar volume of water
| (3) |
directly follows from the requirement that the volume fractions add up to unity . The water concentration, , is obtained from (20)
| (4) |
Vapor-pressure osmometry
Osmolyte concentrations for the osmotic coefficient measurements were determined from the density measurements described in the previous section. The water vapor pressure was measured in a Vapro 5520 Osmometer (28–30) (Wescor, Stoneham, MA) modified as described previously (19). The instrument determines the dew point of the water in the gas phase above the solution. The dew point is a measure of the chemical activity of the water, , which is expressed in terms of osmolality, , where is the osmolality, and ϕ the osmotic coefficient. The measured osmolality values were divided by the total molality to obtain the osmotic coefficient, which is a measure of the deviation of water chemical activity from thermodynamic ideality (proportionality between and concentration).
The osmotic coefficient data were fitted by a polynomial and converted to molal activity coefficients, , through the Gibbs-Duhem relation (31), and to molar activity coefficients, , by the relation . The molar activity coefficients were then fit to an activity coefficient model based on partition-function terms up to second order (8)
| (5) |
where is an interaction parameter, and and are the nominal concentrations of osmolyte in states described by the first- and second-order partition-function terms, respectively. In the simplest interpretation of Eq. 5, is the volume of an individual hydrated osmolyte molecule in solution, is the volume of a hydrated pair, and is the affinity between osmolyte molecules (8), though this interpretation is likely oversimplified (32).
KB integrals
To resolve the mechanistic basis of osmolyte behavior, it is very important to gain insight about the degree to which these compounds interact with each other and with water. The relative proximity of molecules in solution can be calculated from experimental thermodynamic data through KB theory (6) or, more specifically, inverse KB theory (7). This rigorous theory relates chemical activities and volumetric properties to so-called KB integrals, which are integrated pair-correlation functions. For osmolytes, these integrals are usually negative, because the centers of mass of molecules must be spaced away from each other due to the impossibility of two atoms occupying the same space (10,33,34). However, if osmolytes tend to associate in solution, they may end up being as closely or even more closely associated than randomly distributed centers of mass would be, leading to zero or positive KB integrals. This is the case for urea and glycine, for example (10,16).
The KB integrals can be calculated from experimental data by (10)
| (6) |
for the self-solvation of osmolytes (osmolation),
| (7) |
for the self-hydration of water, and
| (8) |
for mutual solvation of water and osmolyte (i.e., osmolyte hydration or water osmolation), where R is the gas constant, T is the absolute temperature, κ is the compressibility, and and are defined by and ; is the chemical activity of compound i, and is its molar activity coefficient.
We determine and for osmolyte and water, respectively, using density data as described above; and we determine and for an osmolyte using the VPO data, also as described above. To determine and for water, we use (valid by definition), and from Eq. 8, we obtain . The compressibility, κ, is very small for aqueous solutions and negligible for our purposes (35). Rather than dropping the compressibility term completely, we use the compressibility of plain water (36).
What do these mean? There are three kinds of contributions to : the partial molar volume, ; the solution nonideality, or ; and the compressibility term, . The partial molar volume is the most fundamental contribution, primarily accounting for the fact that molecules take up space and cannot overlap. That is why this contribution to is negative, i.e., based on the presence of one molecule, less space is available to all others. The next contribution, the solution nonideality, represents additional repulsions or attractions between molecules. Repulsions are represented by positive and attractions by negative (positive and negative slopes, respectively, of the activity coefficient versus concentration). The compressibility term is needed for a different reason. In a dilute gas, the partial molar volumes include large contributions from the empty space between molecules, and the compressibility term corrects for this.
Determination of van der Waals volumes
The most fundamental type of interaction between molecules is hard-core repulsion. The osmolyte trimethylamine N-oxide (TMAO) was recently shown to obey such simple behavior (11). To compare the behavior of the osmolytes to this limiting case, we need to know the van der Waals volumes of the osmolytes. van der Waals volumes were calculated either from the effective spherical radii of the osmolytes (20) or by using MOLMOL (37). Where necessary, hydrogen atoms were added using PRODRG (38). Coordinate files were obtained from the HIC-Up database (39). For GPC, we used a truncated phosphatidylcholine without the fatty acid chains.
Normalizing the solvation of osmolytes to the limiting case of hard-core repulsion facilitates the comparison between molecules of very different size. Moreover, we will see that some of the osmolytes approximate well the thermodynamics of hard-core particles, just as TMAO does (11). Such a finding is very significant from a mechanistic perspective, since it highly suggests that these osmolytes affect proteins through an entropic mechanism (40).
Results and Discussion
The experimental densities (and solubilities) and osmotic coefficients are shown in Figs. 2 and 3, respectively, and the corresponding parameters for Eqs. 1 and 5 are given in Tables 1 and 2. The solubilities of taurine and myo-inositol are comparably low (41), but that for GPC is high to a degree that it is impractical to measure for viscosity reasons. In a similar way, taurine and myo-inositol group together with respect to the osmotic coefficient (Fig. 3 A), which is virtually identical for them. GPC has an extraordinarily large osmotic coefficient as a function of concentration, as well as a high molar activity coefficient compared to the other renal osmolytes (Fig. 3 B).
Figure 3.
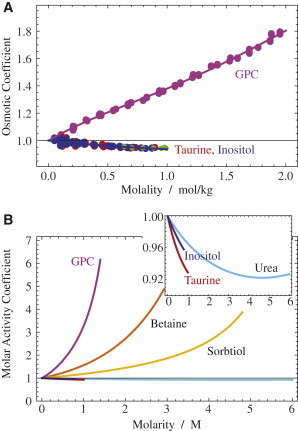
Osmotic and activity coefficients of renal osmolytes. (A) Osmotic coefficients of taurine, myo-inositol, and GPC. Polynomial fits are shown as lines. Previous data for myo-inositol (41) are shown as smaller circles. (B) Molar activity coefficients of six renal osmolytes calculated according to Eq. 5 using the parameters from Table 2 and previous publications (8,10). (Inset) Magnification of the lowest three molar activity coefficients. To see this figure in color, go online.
Table 1.
Density fitting results to Eq. 1 in mL/mol for GPC, taurine, and myo-inositol
| 182.8 | 71.2 | ||
|---|---|---|---|
| /(10−3/m) | 241 | /(1/m) | 1.88 |
| /(10−3/m2) | -52.5 | /(1/m2) | -1.25 |
| /(10−3/m3) | 14.5 | 101.0 | |
| /(10−3/m4) | -0.61 | /(1/m) | 2.40 |
Values are given in mL/mol. g, GPC; t, taurine; i, inositol.
Table 2.
Molar-activity coefficient fitting results to Eq. 5, crystal molarities, , and molecular weights,
| GPC | taurine | myo-inositol | |
|---|---|---|---|
| c1 (M) | 0.62 | ||
| c2 (M) | 1.97 | 19.44 | |
| pg2 | 0.55 | 1.025 | 1.045 |
| cm (M) | 5.13 | 13.66 | 8.74 |
| Mr (Da) | 257.22 | 125.15 | 180.16 |
As usual for osmolytes (8), the densities are close to linear functions of their molarity (Fig. 2, dashed lines). That means that the partial molar volumes do not depend much on osmolyte concentration (8). Fig. 4 shows the partial molar volumes for GPC, myo-inositol, and taurine along with their partial molar volumes in the crystalline state (dashed lines) (42–44). It is noteworthy that the volume of myo-inositol in solution is >10% smaller than in the crystalline state, whereas the deviation is only ∼6% and 3% for GPC and taurine, respectively.
Figure 4.
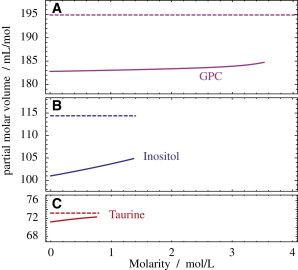
Partial molar volumes of renal osmolytes GPC (A), myo-inositol (B), and taurine (C). The solution volumes (solid lines) were plotted using the parameters from Table 1 in Eq. 2, and the crystalline limits (dashed lines) (42–44) are taken from Table 2 as . To see this figure in color, go online.
The experimental data can be translated into solvation patterns that are discussed below for each of the protecting renal osmolytes.
Inositol
Protein-stabilizing osmolytes, including polyols, have been found to exhibit increasing activity coefficients (8) and osmotic coefficients (9) as a function of concentration. It is therefore unexpected to find the opposite case for the protein stabilizer myo-inositol (45) (Fig. 3). Its decreasing osmotic and activity coefficients point to the tendency of solutes to associate (8), as also evidenced by its very high (almost positive) KB integrals of self-solvation, GOO, in Fig. 5.
Figure 5.
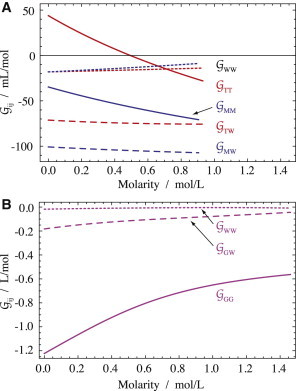
Solvation of taurine, myo-inositol, and GPC. Kirkwood-Buff integrals for osmolyte self-solvation, GOO (solid lines), hydration, GOW (dashed lines), and water self-hydration, GWW (dotted lines), were calculated using Eqs. 6–8, respectively. (A) Solvation of taurine and myo-inositol. (B) Solvation of GPC. The generic index O for osmolyte is replaced in the figure by the appropriate initial for each osmolyte. To see this figure in color, go online.
Moreover, it has been found that the hydroxyl oxygens of an inositol isomer, scyllo-inositol, fit very well into the tetrahedral structure of water (46–48), arguing for optimal hydration and thus minimal self-solvation, again at variance with Figs. 3 and 5. However, though the positions of the oxygens match the water crystal structure, the resulting orientations of the hydroxyl groups appear to be geometrically unfavorable for H-bond formation with the surrounding water molecules. Thus, hydration of inositols should be relatively difficult. Indeed, molecular dynamics simulations have shown that among polyols, both myo-inositol and scyllo-inositol interfere substantially with tetrahedral arrangements of surrounding waters (49). Inositols lead to more distorted H-bonds, and have more of a tendency than other polyols to form interpolyol H-bonds (49). Such association would be highly consistent with the high self-solvation (GOO) shown in Fig. 5. In addition, another computational study found a lower hydration of hydroxylated cyclohexane rings (such as in inositols) compared to cyclopyranoses (50), which adds more support for the idea that inositol hydration is problematic, making intermolecular H-bonding more likely. Difficulties in H-bonding due to geometric constraints have previously been found for guanidinium ions (51,52). Myo-inositol may be another example of such issues.
Compared to other carbohydrates, myo-inositol has another peculiar property. We find that its partial molar and van der Waals volumes are within only 10% of each other, which means that the density of water around myo-inositol must be particularly high. For comparison, the partial molar volumes of glycerol, sorbitol, glucose, and sucrose are between 25% and 40% higher than their van der Waals volumes. The crystalline state of myo-insitol, in contrast, is relatively unremarkable, with a solid-state partial molar volume (114.4 mL/mol (42)) that is ∼24% larger than its van der Waals volume. This is a normal value, given that the partial molar volumes of the above-quoted carbohydrates are essentially unchanged between solid state and aqueous solution (8) over the same range of 25–40%. Thus, the unusual properties of myo-inositol are specific for its aqueous context.
The molar solubility of scyllo-inositol is ∼8.6 times lower than that of myo-inositol. Based on the high symmetry of scyllo-inositol, its configuration integral should be sixfold lower in free solution (53), which almost completely explains the difference in solubility. Then, either the crystal and solution properties of these two inositols are remarkably similar, or (less likely) their differences cancel out fortuitously.
Taurine
Taurine shows an even stronger associative trend than myo-inositol (positive GTT in Fig. 5), as also seen in the decreasing osmotic and activity coefficients (Fig. 3). This is not as unexpected as in the case of inositol, since other amino acids, such as glycine, also show an associative trend (8). In fact, at one time, decreasing osmotic coefficients were used to infer association between amino acids in aqueous solution (54).
Consistent with our data, the osmotic coefficient at the freezing point was previously found to decrease with concentration (55). The solubility of taurine, however, was cited in one study as 840 mM, but without clear reference to the method of measuring the solubility (56). We find a slightly lower solubility of 760 mM.
Hydrogen bonds in taurine crystals are both intramolecular and intermolecular, and the latter are particularly strong (57). Based on vibrational spectra, it is likely that intermolecular H-bonds are also strong in free solution (58). These findings agree well with our observations.
GPC
GPC behaves very differently from myo-inositol and taurine. The self-solvation of GPC, GOO, is large and negative, indicating strong mutual exclusion of GPC molecules (Fig. 5). This osmolyte is a trimethylamine. The best studied osmolyte in this class, TMAO dihydrate (TMAO • 2H2O), has been found to resemble hard spheres in its solvation (11). The limiting hard-sphere solvation value for GOO at 0 M osmolyte concentration is (11,59). Fig. 6 compares GOO to the hard-sphere limit for multiple osmolytes. It turns out that all trimethylamines (Fig. 6, red) are set apart as a group that closely resembles hard spheres in behavior.
Figure 6.
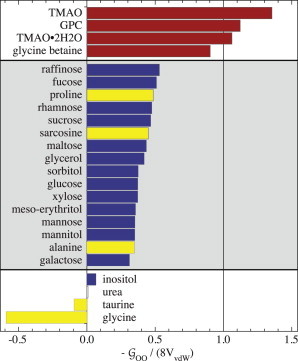
Comparison of osmolyte self-solvation with hard-sphere limit. For hard-spheres, GOO = −8VvdW in the limit of 0 M osmolyte, where VvdW is the van der Waals volume of the osmolyte (11,59). The osmolytes fall into three groups, as indicated by the gray or white background. All trimethyl-amines are in the top group. In the bottom two groups, carbohydrates are indicated in darker color, and amino acids in lighter color. To see this figure in color, go online.
The trimethylamine osmolytes have in common the inaccessibility of one potential H-bonding or ionic interaction site, the nitrogen, due to the three methyl groups. Accordingly, the H-bonding opportunities are somewhat limited in GPC. In the crystal, it does not form any intramolecular H-bonds, and only two intermolecular H-bonds between the two hydroxyl groups and phosphates have been reported (44). According to our data, it is likely also that there are no significant H-bonds between GPC molecules in aqueous solution. This is based on the finding that they solvate each other in a manner comparable to that observed in rigid, inert bodies (Fig. 6).
Betaine
The solvation of glycine-betaine has been reported previously (10). Here, we note that this trimethylamine is among those compounds that are characterized by hard-sphere-like volume exclusion, as seen in Fig. 6. Dielectric relaxation experiments have shown only two relaxation processes in concentrated aqueous glycine betaine solutions, strongly suggesting that no association between glycine-betaine molecules occurs in solution (60), as one would expect for a hard-sphere-like solvation.
An additional illustration of the grouping of osmolytes is shown in Fig. 7. The abscissa quantifies by how many van der Waals volumes the self-solvation of the osmolytes differs from their hydration. Trimethylamines cluster at large negative values because of their strong self-exclusion. It is seen that betaine merges with the other trimethylamines at higher volume fractions, after starting out with a little less self-exclusion. All osmolytes converge to very similar values at volume fractions of unity, as indicated at the righthand side of the figure.
Figure 7.
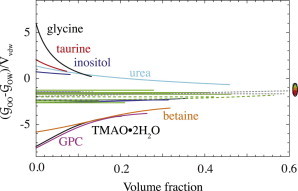
Groups of osmolyte solvation behavior. The abscissa shows by how many osmolyte van der Waals volumes the osmolyte self-solvation GOO exceeds its hydration GOW. The marks on the righthand side indicate , the limit to which the values converge at volume fractions of 1 for the pure (crystalline or liquid) osmolytes (the values of GOO and GOW at the limit of 0 M water are and ; see Rösgen et al. (10)). The middle group of lines represents proline, sarcosine, and alanine (dark solid lines); glycerol, sorbitol, mannitol, and erythritol (short-dashed lines); sucrose, maltose, and raffinose (long-dashed lines); and xylose, fucose, rhamnose, glucose, galactose, and mannose (light solid lines). To see this figure in color, go online.
Fig. 7 also shows the group of self-interacting osmolytes, which are at positive values. The reason that the values are positive is twofold, based on GOW on one hand and GOO on the other. These KB integrals both contribute to the ordinate in Fig. 7, . The hydration, , is negative (and is positive), because osmolytes take space and thus there is a deficit of water molecules around the center of mass of each osmolyte. On top of this positive contribution to the ordinate of Fig. 7, the KB integral of osmolyte self-solvation, GOO, becomes less and less negative with increasing self-interaction, and may even become positive (as seen, e.g., for taurine in Fig. 5). Note that this self-interacting group of osmolytes includes both protein stabilizers, such as myo-inositol, and the denaturant urea.
Sorbitol
The remaining protecting renal osmolyte, sorbitol, is a member of the middle group in both Fig. 6 and Fig. 7. In this group, the self-solvation does not compensate excluded volume effects to the same degree as in the group containing taurine, inositol, urea, and glycine. A statistical thermodynamic investigation of the activity coefficient of sorbitol found that its effective size in solution is larger than expected, which was taken as evidence for a strong hydration (8). On the other hand, molecular dynamics simulations found that at high sorbitol concentrations, there are on average 1.5 hydrogen bonds between individual sorbitol molecules (61). Thus, it seems that both exclusion and association play a significant role for sorbitol, as expected from Fig. 7.
Interactions with other molecules
Now, what can be concluded regarding the interaction of the renal osmolytes with other classes of molecules, such as proteins, nucleic acids, metabolites, etc? The solvation of each osmolyte is a symptom of its interaction with water versus molecules of its own kind. For instance, osmolytes with a strong hydration are more likely than less hydrated osmolytes to retain this preference in the presence of other molecules. This is the basis of the previously established rule that self-excluding osmolytes (those with high osmotic and activity coefficients) are protein stabilizers, whereas denaturants are self-associating (have low osmotic and activity coefficients) (8,9). However, this is only a general trend, for a variety of reasons.
Only a limited subset of types of possible interaction is represented in binary water-osmolyte solutions. For example, glycine betaine was found to interact particularly favorably with aromatic protein side chains (18,21), probably due to cation-pi interactions (62). Such interactions are of course not possible and not sampled in the absence of aromatic compounds.
In the case of taurine, its associating trend correlates with a destabilizing effect, but not for all classes of molecules. It destabilizes DNA (55) but shows a stabilizing (55,63,64), or only slightly destabilizing (65), effect against protein denaturation. In a similar way, glycine also exerts opposite effects on DNA and histones (55). Glycine betaine has also been suggested as a tool for differentiating between protein interactions and DNA interactions, based on such opposing effects on different chemical types of molecular surface (66).
Data are scarce on the interaction of myo-inositol with macromolecules. This osmolyte has less of a stabilizing effect on lysozyme than does sorbitol (45). Based on our data, this difference can be rationalized in two ways. The association trend of inositol can be extrapolated to interactions with proteins, thus reducing the exclusion of inositol. Such reduction in preferential interaction translates to less of a stabilizing effect on proteins. Also, the activity coefficient of myo-inositol is lower than that of sorbitol. Consequently, sorbitol shows a stronger increase in chemical activity with concentration, thereby enhancing its effect on proteins (22).
It makes sense that renal osmolytes show such diverse solvation trends. The presence of high intracellular urea disturbs many kinds of biomolecules, and it is unlikely that any one osmolyte can uniformly counter the effect of urea on all those classes of molecules simultaneously. Since there are five renal osmolytes in addition to urea, it would be possible to affect up to five classes of biomolecules by mixing the osmolytes to different ratios and total concentrations. Alternatively, one can assume that five classes of molecular interactions can be affected.
Conclusions
There are five intracellular renal protecting osmolytes, and it has not been quite clear why so many are used by the kidney, and what the significance of their changing ratios and concentrations is. With this study, we reveal that these osmolytes are quite diverse with respect to their solvation patterns even in simple, binary osmolyte-water solutions. Specifically, they fall into three distinct groups with respect to their tendency to either self-exclude or accumulate around each other. Considering in addition the interaction of the osmolytes with macromolecules differentiates these cosolutes further. Thus, it is likely that specific mixtures of renal osmolytes can target particular sets of macromolecular surface groups. In contrast, it is unlikely that any individual osmolyte could uniformly target sets of cellular biomolecules. Therefore, it is very plausible that the function of the renal osmolyte cocktail is to simultaneously protect multiple types of macromolecules and metabolites from the detrimental effects of urea.
Acknowledgments
We thank Andrew Noel and Samantha Preston for helping with some of the density measurements. The content of this article is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Fig. 1 was made with the University of California, San Francisco Chimera package.
Research reported in this publication was supported by the National Institute of General Medical Sciences (NIGMS) of the National Institutes of Health under award number R01-GM049760. Chimera was developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (supported by NIGMS P41-GM103311).
Footnotes
This is an Open Access article distributed under the terms of the Creative Commons-Attribution Noncommercial License (http://creativecommons.org/licenses/by-nc/2.0/), which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
References
- 1.Garcia-Perez A., Burg M.B. Renal medullary organic osmolytes. Physiol. Rev. 1991;71:1081–1115. doi: 10.1152/physrev.1991.71.4.1081. [DOI] [PubMed] [Google Scholar]
- 2.Yancey P.H., Burg M.B. Distribution of major organic osmolytes in rabbit kidneys in diuresis and antidiuresis. Am. J. Physiol. 1989;257:F602–F607. doi: 10.1152/ajprenal.1989.257.4.F602. [DOI] [PubMed] [Google Scholar]
- 3.Nakanishi T., Uyama O., Sugita M. Osmotically regulated taurine content in rat renal inner medulla. Am. J. Physiol. 1991;261:F957–F962. doi: 10.1152/ajprenal.1991.261.6.F957. [DOI] [PubMed] [Google Scholar]
- 4.Burg M.B., Kador P.F. Sorbitol, osmoregulation, and the complications of diabetes. J. Clin. Invest. 1988;81:635–640. doi: 10.1172/JCI113366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Peterson D.P., Murphy K.M., Yancey P.H. Effects of dietary protein and salt on rat renal osmolytes: covariation in urea and GPC contents. Am. J. Physiol. 1992;263:F594–F600. doi: 10.1152/ajprenal.1992.263.4.F594. [DOI] [PubMed] [Google Scholar]
- 6.Kirkwood J.G., Buff F.P. The statistical mechanical theory of solutions. I. J. Chem. Phys. 1951;19:774–777. [Google Scholar]
- 7.Ben-Naim A. Inversion of the Kirkwood-Buff theory of solutions: application to water-ethanol system. J. Chem. Phys. 1977;67:4884–4890. [Google Scholar]
- 8.Rösgen J., Pettitt B.M., Bolen D.W. Uncovering the basis for nonideal behavior of biological molecules. Biochemistry. 2004;43:14472–14484. doi: 10.1021/bi048681o. [DOI] [PubMed] [Google Scholar]
- 9.Canchi D.R., Jayasimha P., Garcia A.E. Molecular mechanism for the preferential exclusion of TMAO from protein surfaces. J. Phys. Chem. B. 2012;116:12095–12104. doi: 10.1021/jp304298c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rösgen J., Pettitt B.M., Bolen D.W. An analysis of the molecular origin of osmolyte-dependent protein stability. Protein Sci. 2007;16:733–743. doi: 10.1110/ps.062671607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rösgen J., Jackson-Atogi R. Volume exclusion and H-bonding dominate the thermodynamics and solvation of trimethylamine-N-oxide in aqueous urea. J. Am. Chem. Soc. 2012;134:3590–3597. doi: 10.1021/ja211530n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tanford C. Extension of the theory of linked functions to incorporate the effects of protein hydration. J. Mol. Biol. 1969;39:539–544. doi: 10.1016/0022-2836(69)90143-0. [DOI] [PubMed] [Google Scholar]
- 13.Timasheff S.N. The control of protein stability and association by weak interactions with water: how do solvents affect these processes? Annu. Rev. Biophys. Biomol. Struct. 1993;22:67–97. doi: 10.1146/annurev.bb.22.060193.000435. [DOI] [PubMed] [Google Scholar]
- 14.Schellman J.A. The thermodynamics of solvent exchange. Biopolymers. 1994;34:1015–1026. doi: 10.1002/bip.360340805. [DOI] [PubMed] [Google Scholar]
- 15.Courtenay E.S., Capp M.W., Record M.T., Jr. Thermodynamic analysis of interactions between denaturants and protein surface exposed on unfolding: interpretation of urea and guanidinium chloride m-values and their correlation with changes in accessible surface area (ASA) using preferential interaction coefficients and the local-bulk domain model. Proteins, Suppl 4. 2000:72–85. doi: 10.1002/1097-0134(2000)41:4+<72::aid-prot70>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 16.Chitra R., Smith P.E. Preferential interactions of cosolvents with hydrophobic solutes. J. Phys. Chem. B. 2001;105:11513–11522. [Google Scholar]
- 17.Shimizu S. Estimating hydration changes upon biomolecular reactions from osmotic stress, high pressure, and preferential hydration experiments. Proc. Natl. Acad. Sci. USA. 2004;101:1195–1199. doi: 10.1073/pnas.0305836101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Auton M., Bolen D.W. Predicting the energetics of osmolyte-induced protein folding/unfolding. Proc. Natl. Acad. Sci. USA. 2005;102:15065–15068. doi: 10.1073/pnas.0507053102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Harries D., Rösgen J. A practical guide on how osmolytes modulate macromolecular properties. Methods Cell Biol. 2008;84:679–735. doi: 10.1016/S0091-679X(07)84022-2. [DOI] [PubMed] [Google Scholar]
- 20.Auton M., Bolen D.W., Rösgen J. Structural thermodynamics of protein preferential solvation: osmolyte solvation of proteins, aminoacids, and peptides. Proteins. 2008;73:802–813. doi: 10.1002/prot.22103. [DOI] [PubMed] [Google Scholar]
- 21.Guinn E.J., Pegram L.M., Record M.T., Jr. Quantifying why urea is a protein denaturant, whereas glycine betaine is a protein stabilizer. Proc. Natl. Acad. Sci. USA. 2011;108:16932–16937. doi: 10.1073/pnas.1109372108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rösgen J., Pettitt B.M., Bolen D.W. Protein folding, stability, and solvation structure in osmolyte solutions. Biophys. J. 2005;89:2988–2997. doi: 10.1529/biophysj.105.067330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.MacMillen R.E., Lee A.K. Australian desert mice: independence of exogenous water. Science. 1967;158:383–385. doi: 10.1126/science.158.3799.383. [DOI] [PubMed] [Google Scholar]
- 24.Nakanishi T., Balaban R.S., Burg M.B. Survey of osmolytes in renal cell lines. Am. J. Physiol. 1988;255:C181–C191. doi: 10.1152/ajpcell.1988.255.2.C181. [DOI] [PubMed] [Google Scholar]
- 25.Levillain O., Schmolke M., Guder W. Influence of dehydratation on glycerophosphorylcholine and choline distribution along the rat nephron. Pflügers Arch. 2001;442:218–222. doi: 10.1007/s004240100534. [DOI] [PubMed] [Google Scholar]
- 26.Pettersen E.F., Goddard T.D., Ferrin T.E. UCSF Chimera—a visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 27.Liu Y., Bolen D.W. The peptide backbone plays a dominant role in protein stabilization by naturally occurring osmolytes. Biochemistry. 1995;34:12884–12891. doi: 10.1021/bi00039a051. [DOI] [PubMed] [Google Scholar]
- 28.Zhang W., Capp M.W., Record M.T., Jr. Thermodynamic characterization of interactions of native bovine serum albumin with highly excluded (glycine betaine) and moderately accumulated (urea) solutes by a novel application of vapor pressure osmometry. Biochemistry. 1996;35:10506–10516. doi: 10.1021/bi960795f. [DOI] [PubMed] [Google Scholar]
- 29.Courtenay E.S., Capp M.W., Record M.T., Jr. Vapor pressure osmometry studies of osmolyte-protein interactions: implications for the action of osmoprotectants in vivo and for the interpretation of “osmotic stress” experiments in vitro. Biochemistry. 2000;39:4455–4471. doi: 10.1021/bi992887l. [DOI] [PubMed] [Google Scholar]
- 30.Hong J., Capp M.W., Record M.T. Preferential interactions in aqueous solutions of urea and KCl. Biophys. Chem. 2003;105:517–532. doi: 10.1016/s0301-4622(03)00112-1. [DOI] [PubMed] [Google Scholar]
- 31.Gibbs J. Volume 1. Ox Bow Press; Woodbridge, CT: 1993. (The Scientific Papers of J. Williard Gibbs). [Google Scholar]
- 32.Kokubo H., Rösgen J., Pettitt B.M. Molecular basis of the apparent near ideality of urea solutions. Biophys. J. 2007;93:3392–3407. doi: 10.1529/biophysj.107.114181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rösgen J. Molecular basis of osmolyte effects on protein and metabolites. Methods Enzymol. 2007;428:459–486. doi: 10.1016/S0076-6879(07)28026-7. [DOI] [PubMed] [Google Scholar]
- 34.Rösgen J. Molecular crowding and solvation: direct and indirect impact on protein reactions. Methods Mol. Biol. 2009;490:195–225. doi: 10.1007/978-1-59745-367-7_9. [DOI] [PubMed] [Google Scholar]
- 35.Matteoli E., Lepori L. Solute solute interactions in water. 2. An analysis through the Kirkwood-Buff integrals for 14 organic solutes. J. Chem. Phys. 1984;80:2856–2863. [Google Scholar]
- 36.Lide D. CRC Press; Boca Raton, FL: 2004. CRC Handbook of Chemistry and Physics. [Google Scholar]
- 37.Koradi R., Billeter M., Wüthrich K. MOLMOL: a program for display and analysis of macromolecular structures. J. Mol. Graph. 1996;14:51–55. doi: 10.1016/0263-7855(96)00009-4. 29–32. [DOI] [PubMed] [Google Scholar]
- 38.Schüttelkopf A.W., van Aalten D.M. PRODRG: a tool for high-throughput crystallography of protein-ligand complexes. Acta Crystallogr. D Biol. Crystallogr. 2004;60:1355–1363. doi: 10.1107/S0907444904011679. [DOI] [PubMed] [Google Scholar]
- 39.Kleywegt G.J., Jones T.A. Databases in protein crystallography. Acta Crystallogr. D Biol. Crystallogr. 1998;54:1119–1131. doi: 10.1107/s0907444998007100. [DOI] [PubMed] [Google Scholar]
- 40.Cho S.S., Reddy G., Thirumalai D. Entropic stabilization of proteins by TMAO. J. Phys. Chem. B. 2011;115:13401–13407. doi: 10.1021/jp207289b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Barone G., Cacace P., Elia V. Excess thermodynamic properties of myo-inositol and polyhydric alcohols in water at 25°C. Carbohyd. Res. 1983;119:1–11. [Google Scholar]
- 42.Rabinowitz I.N., Kraut J. The crystal structure of myo-inositol. Acta Crystallogr. 1964;17:159–168. [Google Scholar]
- 43.Sutherland H., Young D. The crystal and molecular structure of taurine. Acta Crystallogr. 1963;16:897–901. [Google Scholar]
- 44.Abrahamsson S., Pascher I. Crystal and molecular structure of L-α-glycerylphosphorylcholin. Acta Crystallogr. 1966;21:79–87. doi: 10.1107/s0365110x66002366. [DOI] [PubMed] [Google Scholar]
- 45.Romero C., Albis A., Sancho J. Thermodynamic study of the influence of polyols and glucose on the thermal stability of holo-bovine α-lactalbumin. J. Therm. Anal. Calorim. 2009;98:1–7. [Google Scholar]
- 46.Kabayama M.A., Patterson D. The thermodynamics of mutarotation of some sugars: II. Theoretical considerations. Can. J. Chem. 1958;36:563–573. [Google Scholar]
- 47.Warner D.T. Some possible relationships of carbohydrates and other biological components with the water structure at 37°. Nature. 1962;196:1055–1058. [Google Scholar]
- 48.Chaplin M.F. A proposal for the structuring of water. Biophys. Chem. 2000;83:211–221. doi: 10.1016/s0301-4622(99)00142-8. [DOI] [PubMed] [Google Scholar]
- 49.Politi R., Sapir L., Harries D. The impact of polyols on water structure in solution: a computational study. J. Phys. Chem. A. 2009;113:7548–7555. doi: 10.1021/jp9010026. [DOI] [PubMed] [Google Scholar]
- 50.Boscaino A., Naidoo K.J. The extent of conformational rigidity determines hydration in nonaromatic hexacyclic systems. J. Phys. Chem. B. 2011;115:2608–2616. doi: 10.1021/jp110248j. [DOI] [PubMed] [Google Scholar]
- 51.Lim W.K., Rösgen J., Englander S.W. Urea, but not guanidinium, destabilizes proteins by forming hydrogen bonds to the peptide group. Proc. Natl. Acad. Sci. USA. 2009;106:2595–2600. doi: 10.1073/pnas.0812588106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Mason P.E., Neilson G.W., Cruickshank J.M. The hydration structure of guanidinium and thiocyanate ions: implications for protein stability in aqueous solution. Proc. Natl. Acad. Sci. USA. 2003;100:4557–4561. doi: 10.1073/pnas.0735920100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Gilson M.K., Irikura K.K. Symmetry numbers for rigid, flexible, and fluxional molecules: theory and applications. J. Phys. Chem. B. 2010;114:16304–16317. doi: 10.1021/jp110434s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Frankel M. Zur kenntnis der assoziationstendenz von aminosäuren in wässeriger lösung. Biochem. Z. 1930;217:378–388. [Google Scholar]
- 55.Buche A., Colson P., Houssier C. Effect of organic effectors on chromatin solubility, DNA-histone H1 interactions, DNA and histone H1 structures. J. Biomol. Struct. Dyn. 1993;11:95–119. doi: 10.1080/07391102.1993.10508712. [DOI] [PubMed] [Google Scholar]
- 56.Jacobsen J.G., Smith L.H. Biochemistry and physiology of taurine and taurine derivatives. Physiol. Rev. 1968;48:424–511. doi: 10.1152/physrev.1968.48.2.424. [DOI] [PubMed] [Google Scholar]
- 57.Okaya Y. Refinement of the crystal structure of taurine 2-aminoethylsulfonic acid. An example of computer-controlled experimentation. Acta Crystallogr. 1966;21:726–735. [Google Scholar]
- 58.Ohno K., Mandai Y., Matsuura H. Vibrational spectra and molecular conformation of taurine and its related compounds. J. Mol. Struct. 1992;268:41–50. [Google Scholar]
- 59.Rösgen J., Jackson-Atogi R. Correction to volume exclusion and H-bonding dominate the thermodynamics and solvation of trimethylamine-N-oxide in aqueous urea. J. Am. Chem. Soc. 2012;134:14263. doi: 10.1021/ja211530n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Shikata T. Dielectric relaxation behavior of glycine betaine in aqueous solution. J. Phys. Chem. A. 2002;106:7664–7670. [Google Scholar]
- 61.Lerbret A., Mason P.E., Brady J.W. Molecular dynamics studies of the conformation of sorbitol. Carbohydr. Res. 2009;344:2229–2235. doi: 10.1016/j.carres.2009.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Schiefner A., Breed J., Bremer E. Cation-pi interactions as determinants for binding of the compatible solutes glycine betaine and proline betaine by the periplasmic ligand-binding protein ProX from Escherichia coli. J. Biol. Chem. 2004;279:5588–5596. doi: 10.1074/jbc.M309771200. [DOI] [PubMed] [Google Scholar]
- 63.Yancey P.H., Somero G.N. Counteraction of urea destabilization of protein structure by methylamine osmoregulatory compounds of elasmobranch fishes. Biochem. J. 1979;183:317–323. doi: 10.1042/bj1830317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Arakawa T., Timasheff S.N. The stabilization of proteins by osmolytes. Biophys. J. 1985;47:411–414. doi: 10.1016/S0006-3495(85)83932-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Ratnaparkhi G.S., Varadarajan R. Osmolytes stabilize ribonuclease S by stabilizing its fragments S protein and S peptide to compact folding-competent states. J. Biol. Chem. 2001;276:28789–28798. doi: 10.1074/jbc.M101906200. [DOI] [PubMed] [Google Scholar]
- 66.Hong J., Capp M.W., Record M.T., Jr. Use of urea and glycine betaine to quantify coupled folding and probe the burial of DNA phosphates in lac repressor-lac operator binding. Biochemistry. 2005;44:16896–16911. doi: 10.1021/bi0515218. [DOI] [PMC free article] [PubMed] [Google Scholar]


