Abstract
Individuals with severe motor impairments commonly enter text using a single binary switch and symbol scanning methods. We present a new scanning method –Huffman scanning – which uses Huffman coding to select the symbols to highlight during scanning, thus minimizing the expected bits per symbol. With our method, the user can select the intended symbol even after switch activation errors. We describe two varieties of Huffman scanning – synchronous and asynchronous –and present experimental results, demonstrating speedups over row/column and linear scanning.
1. Introduction
With the rise of email, SMS messaging, microblogging and other on-line social media, communicating by text is increasingly important. Fast and accurate text entry is typically achieved with conventional keyboards, such as the longstanding QWERTY keyboard layout. There are, however, users who cannot rely on the direct use of standard keyboards, requiring new technologies to assist them with efficient text entry. Predictive (statistical) models can be used to address efficiency with non-standard keyboards, such as the widely-used T9 system [15], by, for example, automatically disambiguating between symbols that share the same key in a reduced keyboard.
Much of the motivating work on predictive text entry predating the T9 system derives from text entry research in the field of Augmentative and Alternative Communication (AAC) in the 1980s [14, 22, 20]. In AAC, the challenge is to make key access easier for individuals with significant motor impairments who cannot accurately depress small keys. For the same-sized keyboard, fewer keys mean more space for each key and larger targets for direct selection. However, there remain a group of typists with such severe motor impairments that even large keys are in-sufficiently accessible, since they cannot control their hands to directly select any targets. For those typists, AAC research has focused on providing text entry technology through indirect or encoded means, often just requiring a binary (yes/no) response to two choices. Any anatomical site that can be reliably and consistently controlled, such as movement of an eyebrow, jaw, forehead or foot, eyeblink or even a breath, can be leveraged for a binary response. Indirect selection methods, known as keyboard emulation, typically involve systematically scanning through options and eliciting the binary yes/no response at each scanning step [21]. The current paper is focused on new methods for the use of predictive models within such scanning systems.
AAC scanning over character matrices (or grids), such as those shown in Figure 1, has been around since the 1970s. Most systems rely on row/column scanning where a cursor sequentially highlights rows in the matrix, dwelling on each row for a specified period to allow the user to select the row. Once a row has been selected, cells in that row are sequentially highlighted for selection. For example, using the character matrix in Figure 1(a), the sequence of events to enter the letter ‘t’ are given in Figure 2. As each row or cell is highlighted, the system user can choose to activate or not activate the switch – activation means that the target symbol is in the highlighted row or cell; no activation during the specified dwell time means that the target symbol was not in the highlighted region. Scanning with a single switch amounts to assigning a binary code to each symbol in the matrix: switch activation within the dwell time is a ‘yes’ or 1; dwell time expiration with no switch activation is a ‘no’ or 0. For example, the letter ‘t’ has the 8-bit code ‘00010001’ in the grid in Figure 1(a) and the 4-bit code ‘0011’ in the grid in Figure 1(b). In row/column scanning, the codes for all symbols are determined by their position in the matrix. We present pseudocode for a row/column scanning algorithm in Appendix A.
Figure 1.
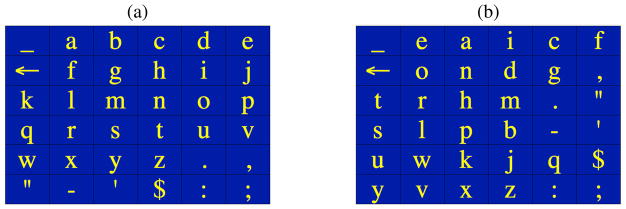
Two spelling matrices: (a) in rough alphabetic order and (b) frequency optimized order. The symbol ‘_’ denotes space; ‘←’ denotes delete.
Figure 2.
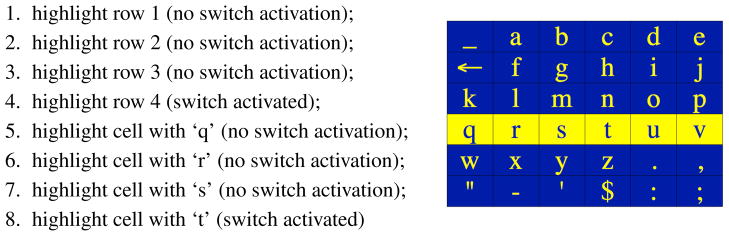
The sequence of events to enter the letter ‘t’ using row/column scanning over the alphabetic ordered grid in Figure 1(a).
Early AAC efforts to optimize the scanning array led to the development of the Tufts Interactive Communicator (TIC) [10, 13] and the Anticipatory TIC (ANTIC) [2]. While the alphabetic ordering in Figure 1(a) has the virtue of relative ease locating the target symbol in the grid, note that it takes 8 actions (switch activation or dwell time expiration) to enter the relatively common letter ‘t’. In the TIC, a frequency based matrix – similar to that shown in Figure 1(b) – was shown to speed text entry rates by placing more frequent symbols closer to the upper left hand corner, where they require fewer actions to enter. Note that the letter ‘t’ would require just 3 rows and 1 column to be highlighted in order to be entered using the matrix in Figure 1(b), in contrast to 4 rows and 4 columns with the matrix in Figure 1(a) (i.e., 4 bits instead of 8 bits in the row/column code).
Frequency ordered grids are an effective technique because faster input can be achieved by assigning shorter codes to likely symbols. However, the letter ‘t’ is not always equally likely – that depends on what has been previously entered. For example, imagine a user has just entered ‘perso’ and is ready to enter the next letter. In this context, the letter ‘n’ is quite likely in English, hence if a very short code is assigned to that letter (e.g., ‘01’), then the user requires only two actions (a ‘no’ and a ‘yes’) to produce the letter, rather than the 5 actions required by the row/column code implicit in the grid in Figure 1(b). Now consider that the probability of the letter ‘u’ is not particularly high overall in English (less than 0.02), but if the previously entered symbol is ‘q’, its probability is very high. Thus, in many contexts, there are other letters that should be assigned the shortest code, but in that particular context, following ‘q’, ‘u’ is very likely, hence it should ideally receive the shortest code.
Common scanning methods, however, present a problem when trying to leverage contextually sensitive language models for efficient scanning. In particular, methods of scanning that rely on highlighting contiguous regions – such as row/column scanning – define their codes in terms of location in the grid, e.g., upper left-hand corner requires fewer keystrokes to select than lower right-hand corner using row/column scanning. To improve the coding in such an approach requires moving characters to short-code regions of the grid. In other words, with row/column scanning methods, the symbol needing the shortest code must move into the upper left-hand corner of the grid after each selection. The Portable Anticipatory Communication Aid (PACA) [16] made use of a bigram character model to perform dynamic grid reorganization after each letter, in order to reduce the number of required switch activations. However, the cognitive load and working memory demands to process letter-by-letter grid reorganizations outweighs any speedup that is achieved through more efficient coding1 [3, 21]. If one assumes a fixed grid, then row/column scanning gains efficiency by frequency organization of the grid, as in Figure 1(b), but cannot use contextually informed models. This is similar to Morse code, which assigns fixed codes to symbols based on overall frequency, without considering context.
In this paper we present a novel scanning method – Huffman scanning – that allows the use of context in establishing binary codes for symbols without requiring dynamic grid reorganization. Rather, highlighted regions are determined by a Huffman code [17] given the probability distribution over symbols, which minimizes the expected code length (see Section 2.2 for background). In other words, the Huffman code provides the shortest codes for the most likely symbols in all contexts, leading to fewer required keystrokes to enter those symbols. While Huffman coding has been used in designing scanning interfaces before (see Section 2.2), this is its first use for fixed grid scanning using contextually dynamic predictive models. Our approach includes a novel method to account for text entry errors at each bit of the code, allowing users to miss their target or mistakenly activate a switch and recover gracefully to enter their target symbol. We show that this approach can provide a large improvement in text entry speed relative to methods that exploit no context in assigning codes (e.g., row/column scanning), as well as relative to linear scanning methods. In addition, we present Huffman scanning methods for asynchronous keyboard emulation, when scanning proceeds at the pace of the individual with an arbitrary amount of dwell time (no timeout). There, too, we show the utility of language models within fixed grid keyboard emulation.
Before presenting our methods and experimental results, we next provide further background on alternative text entry methods, language modeling, and binary coding based on language models.
2. Preliminaries and background
2.1. Alternative text entry
For a comprehensive overview of scanning methods and AAC, we refer the readers to Beukelman and Mirenda [6]; also, [21] is an extensive study on specific methods for speeding up scanning systems, with an excellent review of prior work. In this section we will highlight several key distinctions and findings of particular relevance to this work – in particular, various synchronous and asynchronous indirect selection approaches, and the use of predictive models in AAC.
2.1.1. Indirect selection
Indirect selection strategies allow users to select target symbols through a sequence of simpler operations, typically yes/no responses. This is achieved by scanning through options displayed in the user interface. Beukelman and Mirenda [6] mention circular scanning (around a circular interface), linear scanning (one at a time), and group-item scanning (e.g., row/column scanning to find the desired cell). Another variable in scanning is the speed of scanning – e.g., how long does the highlighting dwell on the options before selecting or advancing. Finally, there are differences in selection control strategy, which can be driven by when a switch is activated (pressed) or released (or both). Beukelman and Mirenda [6] mention automatic scanning, where highlighted options are selected by activating a switch, and advance automatically if the switch is not activated within the specified dwell time; step scanning, where highlighted options are selected when the switch is not activated within the specified dwell time, and advance only if the switch is activated; and directed scanning, where the highlighting moves while the switch is activated and selection occurs when the switch is released. Note that there is some terminological variation in the field, for example directed scanning is also sometimes called user scanning; but these examples serve to illustrate the kinds of system configuration choices that are made. In all of these methods, synchrony with the scan rate of the interface is paramount. Asynchronous scanning requires two kinds of switch activation, one to advance the scanning and one to select. This kind of asynchronous scanning is often achieved via a two-switch step scanning system.
The specific capabilities of each individual is what will drive their best interface option, and speech and language pathologists, occupational therapists, clinical scientists, caregivers and AAC users themselves can all work together to determine the best options for that individual. For example, an individual who has difficulty precisely timing short duration switch activation but can hold a switch more easily might do better with directed scanning. In addition to the ability to produce reliable signals, other considerations when choosing the access method have to do with fatigue and the impact of repeated switch access. A very fast text entry method will not be particularly useful if the individual can only sustain system use over short stretches.
Morse code, with its dots and dashes, is also an indirect selection method that has been used in AAC since the 1970s, and is available in many commercial AAC products. Use of Morse code, however, is far less common than the above mentioned scanning approaches due to the additional cognitive overhead required for code memorization. Once learned, however, this approach can be an effective communication strategy, as discussed with specific examples in [6]. Expert users can enter text at rates above 30 words per minute. Often the codes are entered with switches that allow for easy entry of both dots and dashes, e.g., using two switches, one for dot and one for dash. Morse code is not strictly speaking a binary code, since the duration of pause is used to signal symbol and word boundaries. We will be exploring a similar idea with our asynchronous scanning idea, albeit without the need for memorization and making use of contextual probabilities (see Section 4.4.1).
2.1.2. Predictive models for AAC
Much of the research on the use of predictive statistical language models within the context of AAC has been for word completion/prediction for keystroke reduction [11, 23, 33, 32, 31, 34]. A common scenario for this is allocating a region of the interface to contain a set of suggested words that complete the word the user has begun entering. The expectation is to derive a keystroke savings when the user selects one of the alternatives rather than entering the rest of the letters. The processing load of monitoring a list of possible completions has made controversial the claim that this speeds text entry [1]; yet some results have shown this to speed text entry under certain conditions [31], and word completion is a very common component of AAC keyboard emulation software. Word prediction can be used within either direct or indirect selection systems.
Nantais et al. [26] presented another method for leveraging predictive models in direct selection systems, particularly those that rely upon dwell time for selection. For example, systems where the user controls a cursor using some kind of head or eye tracking system often select the symbol when the cursor dwells on the symbol for some time. The system in [26] dynamically reduced the dwell time for a symbol if the symbol is very likely, significantly speeding text entry speed.
For symbol prediction within a grid scanning interface, in lieu of full-scale grid reorganization – which is a dispreferred solution to this problem [3, 21] –one can allocate a small region to the most likely symbols, similar to the word completion region mentioned above, and integrate the cells in this region into the scanning [2, 12, 21]. Dynamically changing only a small number of cells in the display and leaving the rest static is one way to reduce the processing demands while still achieving some gain from dynamic language models.
One innovative language-model-driven text entry system is Dasher [36], which uses language models and arithmetic coding to present alternative letter targets on the screen with size relative to their likelihood given the history. Users enter text by navigating through target letter regions, while moving eye gaze or mouse cursor from left-to-right. As letters are entered, subsequent letters appear further to the right, again with regions proportional to their likelihood. This can be an extremely effective text entry interface alternative to keyboards, provided the user has sufficient motor control to perform the required systematic visual scanning. The most severely impaired users have lost the voluntary motor control sufficient for such an interface. There is a single switch version of Dasher, which uses a switch to toggle the area of focus between the upper half and lower half of the screen as the means for navigating through the desired region [24].
Another innovative single switch selection method that has been adapted to text entry is Nomon [7], which uses on-screen clocks to visually prompt users to time their switch activation to their target item. Each clock in the display has an arm rotating at the same rate, and an item is selected by activating the switch when the arm is at the noon position in the item’s associated clockface. The precision of switch activation drives the speed of item selection – divergence from the target time yields ambiguity between multiple items, potentially requiring further revolutions to resolve. This approach yields high interface flexibility, in that clocks can be placed within a spelling grid but alternatively at arbitrary locations in the display without altering the item selection method.
Relying on extensive visual scanning, such as that required in dynamically reconfiguring spelling grids or Dasher, or requiring complex or precise gestural feedback from the user renders a text entry interface difficult or impossible to use for those with the most severe impairments. Linear scanning methods can significantly reduce visual complexity by allowing users to monitor only a single location in the interface while making simple decisions about the presence or absence of their target symbol. They are also easily adaptable to using contextual probabilities, which can dictate the order of the linear scan.
2.2. Binary codes for text entry interfaces
2.2.1. Assigning binary codes to symbols
To further explicate the relation between binary coding and scanning, let us revisit in more detail the idea of row/column scanning as a binary code. As stated in the introduction, row/column scanning proceeds by highlighting a subset of the letters in the grid (a row or cell) and waiting for switch activation to indicate whether the target symbol is in the highlighted set. In the grid illustrating row/column scanning in Figure 2, the row containing the set “{q, r, s, t, u, v}” is highlighted. Recall that in row/column scanning each letter has a binary code, e.g., the letter ‘t’ in Figure 2 has code ‘00010001’. The highlighted set is determined by the binary code – all letters with a ‘1’ in their binary code at the current position are highlighted. Different binary codes would give different sets to highlight. For example, a code may have only three letters – say “{a, m, p}” – with a ‘1’ in the current position, hence just those three letters are highlighted. If this code is determined independently of grid configuration, there is no guarantee that the highlighted symbols will form contiguous regions in the grid. See Appendix A for pseudocode of a scanning algorithm based on assigned binary codes.
If we assign codes independently of the grid, there are many ways in which the codes might be assigned. In this paper, we use methods that yield very short codes for the most likely symbols. We use a statistical model to assign probabilities to each symbol (see Section 2.3), then use those probabilities to build a code. Huff-man coding [17] builds a binary code that minimizes the expected number of bits according to the provided distribution. There is a linear complexity algorithm for building this tree given a list of items sorted by descending probability. Another type of binary code, which we will call a linear code, assigns each letter a code consisting of some number of 0’s followed by a single 1. The length of the code is dictated by its rank in the list of items sorted by descending probability. Thus the highest probability symbol would have code ‘1’; the second ranked symbol ‘01’; the third ‘001’; and so on.
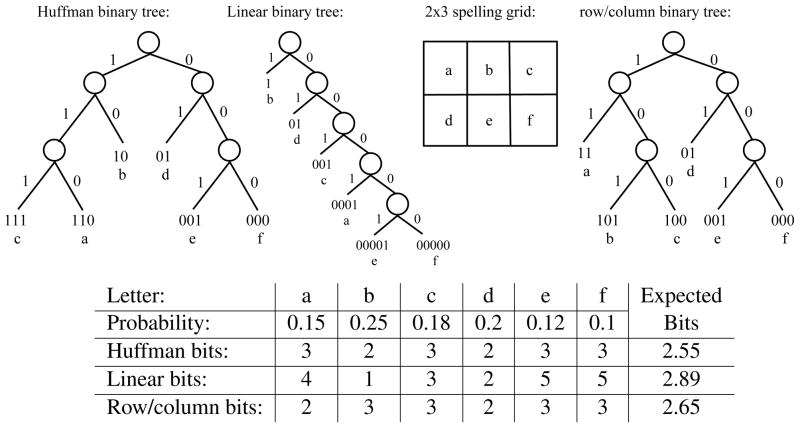
Another way to visualize these codes is through binary trees. In these trees, a left-branch is assigned bit 1 and a right-branch 0. Then the code for each symbol is determined by the bits on the branches from the root of the tree down to the symbol. Figure 3 shows three different binary trees, which yield different binary codes for six letters in a simple, artificial example. Note that the Huffman code yields the minimum expected code length, i.e., no other code can give shorter overall codes according to the distribution2. Linear codes may be shorter for some symbols – such as the code for the letter ‘b’ in Figure 3, which is shorter for the linear code than the Huffman code – but the expected number of bits will typically be longer, due to other symbols (‘e’ and ‘f’ in the example) receiving longer codes. The row/column tree based on the alphabetically ordered 2×3 spelling grid gives expected code length better than the linear code, but worse than the Huffman code. Note that if the ‘a’ and ‘b’ symbols in the grid were swapped, the row/column binary code would have the same expected code length as the Huffman code.
Figure 3.
Three binary trees for encoding letters: (1) Huffman coding; (2) Linear coding; and (3) Row/column coding, based on the presented 2×3 spelling grid.
Linear coding builds a simple right-linear tree (seen in Figure 3) that preserves the sorted order of the set, putting higher probability symbols closer to the root of the tree, thus obtaining shorter binary codes. Linear coding can never produce codes with fewer expected bits than Huffman coding (Huffman is provably minimal), though the linear code may reach the minimum under certain conditions. Linear coding does have the advantage of being suited for linear scanning, whereby a single symbol is highlighted or presented at a time. An interface that presents a single letter at a time in a fixed location reduces the need for extensive visual scanning of the interface. Linear coding is also well-suited to auditory scanning, where options are presented auditorily rather than visually.
2.2.2. Codes for text entry
One can assign various sorts of codes to letters or words, to ease or speed up text entry. Morse code, discussed in the previous section, is one method for assigning codes to letters. This code differs from the binary codes we have discussed in this section in that there are other actions – pauses to indicate letter and word boundaries – beyond the bits in the code itself that are required to input correctly. For an unambiguous strictly binary code, no symbol’s code can be a prefix of another symbol’s code. For example, in Morse code, the letter ‘e’ is entered with a dot; but there are other letters whose code begins with a dot (such as the code for ‘i’ which is two dots), making the code for ‘e’ a prefix for the code of another letter. Without a pause to disambiguate, two consecutive dots could be either two ‘e’s or one ‘i’. In contrast, the binary codes either implicit in row/column scanning or built through the binary trees in Figure 3 are such that no symbol’s binary code is a prefix of another’s.
A lexicon of words can also be coded. In the 1970s, the Phonic Ear Handivoice was a speech generating device where each word was input using a three digit code. Kurtz and Treviranus [19] present a binary tree encoding method which relies on lexicographic ordering judgements from the user – such as whether their target word comes before or after the currently displayed word in an alphabetically ordered list – to navigate through the lexicon. As with Morse code, this method used dots, dashes and pauses to input the code: dot means the target word comes before the current word; dash means it comes after; and a pause means that the node is the target word. Nodes high in the tree are allocated to high frequency words, making them faster to select. This method differs from those presented in this paper by virtue of being closed vocabulary, i.e., one can only enter words from the encoded vocabulary. Also, the code is based on overall word frequency, and does not take into account contextual language model probabilities.
Another way to leverage a closed vocabulary is by eliminating letters that do not produce words in the system dictionary, such as in the Reach Smart Keys™ keyboard. Scanning would then only include those letters that have not been eliminated. For example, if ‘perso’ has been entered, the letter ‘x’ would be eliminated from the keyboard, since ‘persox’ is not in the system vocabulary. This method can help with both direct and indirect selection systems. This is not a method for creating codes for symbols, rather it is the means for reducing the size of the set for which codes are required. With a smaller set of symbols, shorter codes can be the result, but any of the binary coding methods – row/column, Huffman or linear – could be used over this same set. Hence these methods are orthogonal to what we are presenting in this paper, and perhaps quite complementary.
Among the main novelties of this paper is the use of Huffman coding with predictive models for scanning. Huffman coding has been used for scanning systems before [4], but only using overall symbol frequency, similar to the information used to reorganize the grid to optimize row/column scanning in TIC. In [4], they used Huffman codes to derive positions of symbols in the grid, so that scanning according to the resulting binary tree (see Appendix A) always highlighted contiguous blocks of symbols in the grid. In contrast, our approach derives codes without reference to position in the grid, using dynamic n-gram language models, as described in the next section.
2.3. Language modeling for text entry interfaces
Language models assign probabilities to strings in the language being modeled, which has broad utility for many tasks in speech and language processing. The most common language modeling approach is the n-gram model, which estimates probabilities of strings as the product of the conditional probability of each symbol given previous symbols in the string, under a Markov assumption. That is, for a string S = s1 … sn of n symbols, a k+1-gram model is defined as
where the approximation is made by imposing the Markov assumption. Note that the probability of the first symbol s1 is typically conditioned on the fact that it is first in the string. Each of the conditional probabilities in such a model is a multinomial distribution over the symbols in a vocabulary Σ, and the models are typically regularized (or smoothed) to avoid assigning zero probability to strings in Σ*. See [9] for an excellent overview of modeling and regularization methods.
A key requirement in a composition-based text entry interface is that it has an open vocabulary – the user should be able to enter any word, whether or not it is in some fixed dictionary. Further, system users must be able to repair any errors by deleting symbols and re-entering new ones. Using language models to speed indirect character selection is similar to word prediction work discussed in Section 2.1 except for the open vocabulary aspect, i.e., the predictions need to be used in a way that allows for typing of anything. In contrast, a word prediction component must be accompanied by some additional mechanism in place for entering words not in the vocabulary. This paper is focused on the use symbol prediction for that core text entry scanning interface. In principle, the symbols that are being predicted (hence entered) can be from a vocabulary that includes multiple symbol strings such as words, but for this paper we will just be predicting single ASCII and control characters, rather than multiple character strings. The task is actually very similar to the well known Shannon game [30], where text is guessed one character at a time.
Character prediction is done in the Dasher and Nomon interfaces, as discussed in Section 2.1. There is also a letter prediction component to the Sibyl/Sibylle interfaces [29, 35], alongside a separate word prediction component. The letter prediction component of Sibylle (Sibyletter) involves a linear scan of the letters, one at a time in order of probability (as determined by a 5-gram character language model), rather than row/column scanning.
Language modeling for a text entry interface task of this sort is very different from other common language modeling tasks, which include automatic speech recognition and machine translation. This is because, at each symbol in the sentence, the already entered text is given – there is no ambiguity in the prefix string, modulo subsequent repairs. In contrast, in speech recognition, machine translation, optical character recognition or predictive text entry for mobile computing (e.g., T9), the actual prefix string is not known; rather, there is a distribution over possible prefix strings, and a global inference procedure is required to find the best string as a whole. For text entry, once the symbol has been produced and not repaired, the model predicting the next symbol is given the true context. This has several important ramifications for language modeling. First, it creates text data, specific to the user, that can be used to adapt language models for the user. Second, because this is a local model of a character given a history rather than a joint model over the entire sequence, the models trained with maximum likelihood (relative frequency) estimation are optimized for a discriminative objective. Here we will consider n-gram language models of various orders, estimated via smoothed relative frequency estimation (see Section 3.2).
The principal novelties in the current approach are the Huffman scanning method, the principled incorporation of error probabilities into the binary coding approaches, the asynchronous scanning version of Huffman scanning, and the experimental demonstration of how Huffman and linear coding methods compare with de-facto standard row/column scanning approaches.
3. Methods
3.1. Corpora
We prepared two corpora for model training and simulation results: (1) newswire text from the New York Times portion of the English Gigaword corpus (LDC2007T07); and (2) email text from the Enron email dataset (http://www-2.cs.cmu.edu/~enron/). Both corpora were preprocessed for the current evaluation, as detailed below. The key intent of the pre-processing was to yield text that was actually typed, hence useful as training and validation data for English text entry applications. Formatted tabular data, pasted signatures or bylines, automatically generated text and meta-information were removed, as was as much duplication as possible. See Appendix B for specifics on the text normalization used for these two corpora.
3.2. Character-based language models
For this paper, we use character-based n-gram models. Carpenter [8] has an extensive comparison of large scale character-based language models, and we adopt smoothing methods from that paper. It presents a version of Witten-Bell smoothing [37] with an optimized hyperparameter K, which is shown to be as effective as Kneser-Ney smoothing [18] for higher order n-grams (e.g., 12-grams). See Appendix C for specific details on the language modeling approach used in the reported results.
3.3. Binary codes
Given what the system user has entered so far, we can use a character n-gram language model to assign probabilities to all next symbols in the symbol set V. After sorting the set in order of decreasing probability, we can use these probabilities to build binary coding trees for the set. Hence the binary code assigned to each symbol in the symbol set differs depending on what has been entered before. For Huffman coding, we used the algorithm from [27] that accounts for any probability of error in following a branch of the tree, and builds the optimal coding tree even when there is non-zero probability of taking a branch in error. Either linear or Huffman codes can be built from the language model probabilities, and can then be used for a text entry interface, using the algorithm presented in Appendix A.
3.4. Scanning systems
For these experiments, we developed an interface for controlled testing of text entry performance under a range of scanning methods. These include: (i) row/column scanning, both auto scan (button press selects) and step scan (lack of button press selects); (ii) Scanning with a Huffman code, either derived from a unigram language model (no context), or from an n-gram language model; and (iii) Scanning with a linear code, either on the 6×6 grid, or using a single cell for linear scanning, which we term rapid serial visual presentation (RSVP). Each trial involved giving subjects a target phrase with instructions to enter the phrase exactly as displayed. All errors in text entry were required to be corrected by deleting (via ←) the incorrect symbol and re-entering the correct symbol.
Figure 4(a) shows our text entry interface when configured for row/column scanning. At the top of the application window is the target string to be entered by the subject (‘we run the risk of failure’). Below that is the buffer displaying what has already been entered (‘we run t’). Spaces between words must also be entered – they are represented by the underscore in the upper left-hand corner of the grid. Spaces are treated like any other symbol in our language model – they must be entered, thus they are predicted along with the other symbols. Figure 4(b) shows how the display updates when an incorrect character is entered. The errors are highlighted in red, followed by the backarrow to remind users to delete.
Figure 4.

Row/column scanning interface (a) during scanning and (b) after an error in the copy task.
If no row has been selected after passing over all rows, scanning resumes from the top. After row selection, column scanning commences3 from left-to-right; if a column is not selected after three passes over the columns, then row scanning resumes at the following row. Hence, even if a wrong row is selected, the correct symbol can still be entered.
Note that the spelling grid is sorted in unigram frequency order, so that the most frequent symbols are in the upper left-hand corner. This same grid is used in all grid scanning conditions, and provides some non-contextual language modeling benefit to row/column scanning.
Figure 5 shows our text entry interface when configured for Huffman scanning. In this scanning mode, the highlighted subset is dictated by the Huffman code, and is not necessarily contiguous. Not requiring contiguity of highlighted symbols allows the coding to vary with the context, thus allowing use of an n-gram language model. As far as we know, this is the first time that contiguity of highlighting is relaxed in a scanning interface to accommodate Huffman coding. As discussed in Section 2.2, Baljko & Tam [4] used Huffman coding for a grid scanning interface, but using a unigram model to produce a fixed code and the grid layout was selected to ensure that highlighted regions would always be contiguous, thus precluding contextually dependent n-gram models.
Figure 5.

Huffman scanning interface.
It is important to note that the Huffman code is not just highlighting likely symbols. Indeed, in Figure 5, the target letter ‘u’ should be relatively likely, along with the other vowels; but note that just two of five vowels are highlighted. That is because the Huffman algorithm builds a balanced code tree, that is how it optimizes its expected code length. It does this by putting half of the probability mass along one branch of the binary tree and half along the other. Hence likely symbols may go unhighlighted, by virtue of being on the non-highlighted branch of the tree. To make this clearer, suppose we have two very likely symbols: say ‘a’ with probability 0.5, ‘e’ with probability 0.49, and the rest with much lower probability. Then the Huffman code will assign code ‘1’ to ‘a’, and code ‘01’ to ‘e’. Thus the very likely symbol ‘e’ will not be highlighted initially, precisely because this gives it a very short code relative to less likely symbols. This is merely to illustrate that the coding does not highlight all likely symbols.
In Huffman scanning, when the selected set includes just one character, it is entered. As with row/column scanning, when the wrong character is entered, the backarrow symbol must be chosen to delete it. If an error is made in selection that does not result in a entered character – i.e., if the incorrectly selected set has more than one member – then we need some mechanism for allowing the target symbol to still be selected, much as we have a mechanism in row/column scanning for recovering if the wrong row is selected. Until a character is selected, no character is ruled out. The next section details our novel method for recalculating the binary codes based on an error rate parameter.
For linear coding as well, the grids shown in Figures 4 and 5 can be straightforwardly used, by simply highlighting one cell at a time in descending probability order. Additionally, linear coding can be used with an RSVP interface, shown in Figure 6, which displays one character at a time.
Figure 6.

RSVP linear scanning interface.
Each interface needs a scan rate, specifying how long to wait for a button press before advancing. The scan rate for each condition was set for each individual during a training/calibration session (see Section 4.2).
3.5. Errors in Huffman and Linear scanning
In this section we briefly detail how we account for the probability of error in scanning with Huffman and linear codes. The scanning interface has a parameter p, which is the probability that, when a selection is made, it is correct. Thus 1-p is the probability that, when a selection is made, it is incorrect, i.e., an error. Recall that if one selects a single symbol, then that symbol is entered. On the other hand, if one selects a set with more than one symbol, then all symbol probabilities (even those not in the selected set) are updated based on the error probability, and scanning continues. Recall that if an incorrect symbol is selected, the delete symbol must be chosen to delete the incorrect symbol. Three key questions must be answered in such an approach: (1) how are symbol probabilities updated after a keystroke, to reflect the probability of error? (2) how is the probability of backarrow estimated? and (3) when the text entry interface returns to the previous position, where does it pick up the scanning? Here we answer all three questions.
How are symbol probabilities updated after a keystroke, to reflect the probability of error? Consider the Huffman coding tree in Figure 3. If the left-branch (‘1’) is selected by the user, the probability that it was intended is p, whereas the right-branch (‘0’) was intended with probability 1-p. If the original probability of a symbol is q, then the updated probability of the symbol is pq if it starts with a ‘1’ and (1-p)q if it starts with a ‘0’. After updating the scores and re-normalizing over the whole set, we can build a new binary coding tree. The user then selects a branch at the root of the new tree. A symbol is finally selected when the user selects a branch leading to a single symbol. The same approach is used with a linear coding tree.
How is the probability of backarrow estimated? The probability of requiring the backarrow character can be calculated directly from the probability of keystroke error – in fact, the probability of backarrow is exactly the probability of error 1-p. To understand why this is the case, consider that an incorrect symbol can be chosen according to the approach in the previous paragraph only with a final keystroke error. Any keystroke error that does not select a single symbol does not eliminate the target symbol, it merely re-adjusts the target symbol’s probability along with all other symbols. Hence, no matter how many keystrokes have been made, the probability that a selected symbol was not the target symbol is simply the probability that the last keystroke was in error, i.e., 1-p.
Finally, if backarrow is selected, the previous position is revisited, and the probabilities are reset as though no prior selection had been made.
4. Experimental results
4.1. Simulation results
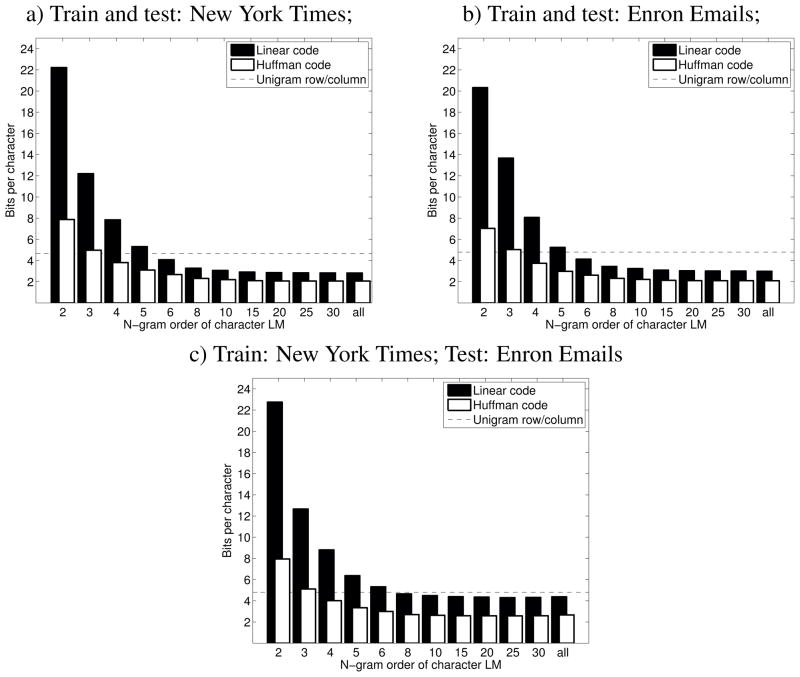
The first set of results are presented in Figure 7. For these trials, we trained our language models on the training corpora specified above, then measured the number of bits (keystrokes) required to enter the text of evaluation corpora. On the y-axis, these bar graphs show the number of bits per character (which correspond to keystrokes per character in our text entry interface) required to enter the test corpus, when given a model of a particular n-gram order trained on the training corpus. The x-axis shows the order of the n-gram model,4 and the y-axis the bits per character. We show results with both linear codes and Huffman codes under three conditions: trained and tested on the New York Times; trained and tested on the Enron Email Dataset; and trained on NYT and tested on Enron. As a baseline, we also show the unigram row/column scanning approach, in which the symbol positions are determined by unigram probability.
Figure 7.
Simulation of bits per character for Huffman and Linear coding for various order n-gram language models, alongside row/column scanning baseline.
As can be seen from these plots, the number of keystrokes per character required with the linear coding is much more than with Huffman coding when the order of the n-gram model is low; but the difference between the two coding methods is small (less than 1 bit for top two bar graphs) when the order of the n-gram model reaches 10–15 and beyond. Both approaches yield substantial improvements over unigram row/column scanning. In Figure 7(c), we see performance with out-of-domain training (New York Times training for Enron test). In this scenario, the difference between the two coding approaches is just under two bits per character for the higher order n-gram models, which also illustrates one take-away point of these results: the better the language model, the less the difference between Huffman coding and linear coding.
4.2. Subjects and scan rate calibration
We recruited 16 native English speakers between the ages of 24 and 48 years, who had not used our text entry interface, are not users of scanning interfaces for text entry, and have typical motor function. Each subject participated in two sessions, one for training and calibration of scan rates; and another for testing. Each session lasted between sixty and ninety minutes. We used the phrase set from [25] to evaluate text entry performance. Of the 500 phrases in that set, 20 were randomly set aside for testing, the other 480 available during training and calibration phases. Five of the 20 evaluation strings were used in this study. We used an Ablenet Jellybean® switch as the binary switch. For these trials, to estimate error rates in modeling, we fixed p = 0.95, i.e., 5% error rate.
The scan rate for row/column scanning is typically different than for Huffman or linear scanning, since row/column scanning methods allow for anticipation: one can tell from the current highlighting whether the desired row or column will be highlighted next. For the Huffman and linear scanning approaches that we are investigating, that is not the case: any cell can be highlighted (or symbol displayed) at any time, even multiple times in sequence. Hence the scan rate for these methods depends more on reaction time than row/column scanning, where anticipation allows for faster rates.
The scan rate also differs between the two row/column scanning approaches (auto scan and step scan, see Section 3.4), due to the differences in control needed to advance scanning with a button press versus selecting with a button press. We thus ran scan rate calibration under three conditions: row/column step scan; row/column auto scan; and Huffman scanning, using a unigram language model. The Huffman scanning scan rate was then used for all of the Huffman and linear scanning approaches.
Calibration involved two stages for each of the three approaches, and the first stage of all three was completed before running the second stage, thus familiarizing subjects with all interfaces prior to final calibration. The first stage of calibration started with slow scan rate (1200 ms dwell time), and whenever a target string was successfully entered, the dwell time was reduced by 200 ms. A target string was successfully entered when it was correctly entered with less than 10% error rate. The subject was given three attempts to enter a string successfully at a given scan rate. If they failed to do so, they were judged to not be able to complete the task at that rate. Failure at a dwell time terminated the first stage for that method and the dwell time at failure was recorded. In the second stage, calibration began with a dwell time 500 ms higher than the dwell time for that method where the subject failed in the first stage. In the second stage, the dwell time decreased by 100 ms increments when target strings were successfully completed. When subjects could not complete the task at a particular dwell time, the dwell time then began increasing by 50 ms increments until they could successfully complete a target string. This was their calibrated scan rate for that scanning method.
Table 1 shows the mean (and std) scan rates (dwell time) for each condition. Step scanning generally had a slower scan rate than auto scanning, and Huffman scanning (unsurprisingly) was slowest.
Table 1.
Calibrated scan rates.
| Scanning condition | Dwell time (ms) mean (std) |
|---|---|
| row/column step scan | 419 (95) |
| row/column auto scan | 328 (77) |
| Huffman and linear scan | 500 (89) |
4.3. Experiment with synchronous scanning
In the testing stage of the protocol, there were six conditions: (1) row/column step scan; (2) row/column auto scan; (3) Huffman scanning with codes derived from the unigram language model; (4) Huffman scanning with codes derived from the 8-gram language model; (5) Linear scanning on the 6×6 spelling grid with codes derived from the 8-gram language model; and (6) linear scan single letter presentation (RSVP) with codes derived from the 8-gram language model. The ordering of the conditions for each subject was randomized. In each condition, instructions were given (identical to instructions during training/calibration phase), and the subjects entered practice phrases until they successfully reached error rate criterion performance (10% error rate or lower), at which point they were given the test phrases to enter. We present these five phrases in Appendix D.
Note that we did not include every permutation of system configuration in the experiment, mainly to keep the number of conditions manageable. In developing the system, we found that using a unigram model with linear scanning required too many keystrokes (as shown in the simulation in Figure 7). In addition, step scanning in both linear scanning conditions requires many more switch activations than auto scanning, and was thought to be too fatiguing for that reason. Hence linear scanning was only presented with auto scanning.
Huffman scanning was also only presented with auto scanning, because the distinction between auto and step scan is somewhat arbitrary in Huffman scanning. To see this, note that the distinction between the ‘1’ and ‘0’ in the binary code is arbitrary: one can “flip” the bits by turning all 1’s into 0’s and vice versa, yielding a code of the same expected length, i.e., the same coding efficiency. Step scan with flipped bits results in a system requiring exactly the same sequence of switch activations and timeouts as an auto scan with the original code. The difference between the two systems would be whether blue in the target cell means press the button or yellow in the target cell means press the button. Thus, there are minor interface differences between step and auto scan control, but in the interests of keeping the number of trials constrained, we opted for just auto control of Huffman scanning. Further, to avoid scenarios where nearly every cell is highlighted in the grid, our interface algorithm flips the bit of codes if the number of cells that would be highlighted outnumbers the number of cells that would not be highlighted. In such a way, the number of highlighted cells is always at most half of the total cells in the grid.
Recall that the task is to enter the test phrase exactly as presented, hence the task is not complete until the phrase has been correctly entered. To avoid nontermination scenarios – e.g., the subject does not recognize that an error has occurred, what the error is, or simply cannot recover from cascading errors – the trial is stopped if the total errors in entering the target phrase reach 20, and the subject is presented with the same target phrase to enter again from the beginning, i.e., the example is reset. Only 2 subjects in the experiment had a phrase reset in this way (just one phrase each), both in row/column scanning conditions. Of course, the time and keystrokes spent entering the text prior to reset are included in the statistics of the condition.
Table 2 shows the mean (and std) of several measures for the 16 subjects. Speed is reported in characters per minute. Bits per character represents the number of keypress and non-keypress (timeout) events that were used to enter the symbol. Note that bits per character does not correlate perfectly with speed, since a non-keypress bit due to a timeout takes the full dwell time, while the time for a keypress bit is less. For any given symbol the bits may involve making an error, followed by deleting the erroneous symbol and reentering the correct symbol. Alternately, the subject may scan past the target symbol, but still return to enter it correctly, resulting in extra keystrokes, i.e., a longer binary code than optimal. In addition to the mean and standard deviation of bits per character, we present the optimal that could be achieved with each method. Finally we characterize the errors that are made by subjects by the error rate, which is the number of incorrect symbols entered divided by the total symbols entered. The long code rate is the percentage of correctly entered symbols for which a longer than optimal code was used to enter the symbol, by making an erroneous selection that does not result in entering the wrong symbol.
Table 2.
Text entry results for 16 users on 5 test strings (total 31words, 145 characters) under six conditions, with calibrated scan rates.
| Scanning condition | Speed (cpm) mean (std) | Bits per character | Error rate mean (std) | Long code rate mean (std) | ||
|---|---|---|---|---|---|---|
| mean (std) | opt. | |||||
| row/column | step scan | 21.2 (3.8) | 8.4 (2.5) | 4.5 | 6.2 (4.4) | 30.4 (17.9) |
| auto scan | 19.6 (3.2) | 8.0 (1.7) | 4.5 | 4.6 (3.0) | 28.9 (13.3) | |
| Huffman | unigram | 12.8 (2.3) | 7.9 (1.7) | 4.4 | 4.4 (2.3) | 35.1 (13.0) |
| 8-gram | 24.5 (3.9) | 4.0 (0.9) | 2.6 | 4.2 (2.2) | 15.4 (12.5) | |
| Linear grid 8-gram | 23.2 (2.4) | 4.1 (0.6) | 3.4 | 2.4 (1.7) | 4.3 (3.4) | |
| RSVP 8-gram | 20.9 (4.4) | 5.5 (2.2) | 3.4 | 7.1 (4.8) | 4.2 (3.7) | |
We also included a short survey, using a Likert scale for responses, and mean Likert scores are shown in Table 3 for four questions: 1) I was fatigued by the end of the trial; 2) I was stressed by the end of the trial; 3) I liked this trial; and 4) I was frustrated by this trial. The Huffman scanning with an 8-gram and linear grid conditions received the highest mean Likert scores for question 3 and the lowest for questions 1, 2 and 4.
Table 3.
Mean Likert scores to survey questions (5 = strongly agree; 1 = strongly disagree)
| Survey Item | Row/Column | Huffman | Linear | |||
|---|---|---|---|---|---|---|
| step | auto | 1-grm | 8-grm | grid | RSVP | |
| I was fatigued by the end of the trial | 3.1 | 1.9 | 3.3 | 1.9 | 1.9 | 2.8 |
| I was stressed by the end of the trial | 2.4 | 2.0 | 2.5 | 1.7 | 1.6 | 2.6 |
| I liked this trial | 2.1 | 3.5 | 2.6 | 3.9 | 3.8 | 2.9 |
| I was frustrated by this trial | 3.4 | 1.8 | 3.1 | 1.7 | 1.7 | 2.9 |
While this is a small study of just 16 subjects overall, several things stand out from the results. First, comparing the three methods using just unigram frequencies to inform scanning (row/column and Huffman unigram), we can see that Huffman unigram scanning is significantly slower than the other two, mainly due to a slower scan rate with no real improvement in bits per character (real or optimal). All three methods have a high rate of longer than optimal codes, leading to nearly double the bits per character than would optimally be required. The error and long code rates are better with a slower scan rate, but none of the methods end up with a much better operating point because of it.
Next, with the use of the 8-gram language model in Huffman scanning, both the optimal bits per character and the difference between real and optimal are reduced, leading to nearly double the speed as with the unigram model. Interestingly, use of the linear code on the grid leads to nearly the same bits per character as Huffman scanning, despite nearly 1 bit increase in optimal bits per character, due to a decrease in error rate and a very large decrease in long code rate. We speculate that this is because highlighting a single cell at a time draws the eye to that cell, making visual scanning much easier.
Finally, despite using the same model, RSVP is found to be slightly slower than the Huffman 8-gram or Linear grid conditions, though commensurate with the row/column scanning, mainly due to an increase in error rate. Monitoring a single cell, recognizing symbol identity and pressing the switch is apparently somewhat harder than finding the symbol on a grid and waiting for the cell to light up.
Note that the users in this experiment were novice users, hence some tasks (such as finding the target letter in the grid) would likely become easier with user expertise. In the training phase, we provided sufficient exposure to each of the methods for the subjects to be able to complete the tasks, not enough to become “experts” in the method. In this study, we controlled for system learning by using novice subjects, controlling the amount of training time, and randomizing conditions at test time. Future work is needed on learning and the effect of expertise.
4.4. Experiment with asynchronous scanning
Because the Huffman code for each symbol changes with the context, users typically cannot anticipate the sequence of required switch activations. In row/column scanning, the binary code of each symbol is obvious from its location in the grid, hence users can anticipate when they will need to trigger the switch. In Huff-man scanning, users must continuously monitor and react when their target cells light up. We believe that this attentional demand leads to scan rates that are typically slower than in row/column scanning. Furthermore, they may contribute to perceived stress.
In this section, we investigate asynchronous Huffman scanning methods, i.e., methods where all of the scanning is self-paced; there is no scan rate that must be matched by the user. Rather than ‘yes’ being a button press and ‘no’ a timeout, these approaches, like Morse code, differentiate between multiple kinds of switch activation. If we measure the time between initial switch activation and release, we can differentiate between short and long presses. For example, if the time between switch activation and release is less than 200 ms (a short press), this can signify a ‘1’; and switch activation of longer duration (a long press) can signify a ‘0’. Alternatively, two switches could be used to differentiate the two kinds of switch activation, as is commonly done in two-switch step scanning. Unlike Morse code, the asynchronous scanning method does not require any pause between letters or words; the codes themselves are unambiguous, since no symbol’s code is the prefix of another’s code (see Appendix A).
There are several benefits to this sort of asynchronous approach. Individuals who struggle with the timing requirements of auto, single-switch step or directed scanning can proceed without having to synchronize their movements to the interface. Individuals can interrupt their communication – e.g., for side talk – for an arbitrary amount of time and come back to it in exactly the same state. Also, it may reduce the stress of constantly monitoring the scanning sequence and reacting to it within the time limits of the interface.
Our novel approach to asynchronous scanning displays the code for each symbol at once as a series of dots and dashes – as used in Morse code – underneath the symbol, as shown in Figure 8, rather than using cell highlighting to prompt the user as in our previous Huffman scanning conditions. These codes differ from Morse code in several key ways. First, since they do not require pauses between symbols (which can be seen as an extra ‘bit’ in the code), they may appear slightly longer. Second, when a new symbol has been typed, new codes are derived for every symbol based on n-gram language models. For example, in Figure 8, the letters ‘r’ and ‘u’ are quite likely continuations of the current word, hence receive shorter codes than the Morse code for those symbols. Since the codes are displayed, no code memorization is required. Because the entire code is displayed, the user can see ahead of time what they’ll have to enter for the target symbol; this contrasts with synchronous Huffman scanning, which requires continuous monitoring of the cell.
Figure 8.
Displaying dots and dashes for Huffman scanning, rather than highlighting cells.
4.4.1. Asynchronous codes
Preliminary results presented in [5] demonstrated that error handling in asynchronous scanning was problematic. Because each code is displayed in full on the screen, the Huffman code cannot be recalculated after every bit, as is done for synchronous Huffman scanning (see Section 3.5). As a result, the most straightforward application of this idea results in a very coarse handling of errors in text entry: once an error is made in the code for the target symbol, it has been ruled out and cannot be entered at that position. To enter the correct symbol, one must enter an incorrect symbol then delete it with the backarrow. User feedback suggested that providing a way to avoid errors would be preferable.
In this paper, we examine two asynchronous Huffman scanning approaches that have new strategies for error recovery. We introduce new leaves into the Huffman code binary tree that represent a reset, which we term “escape” leaves. If the code of an escape leaf is entered, no symbol is selected, and the bit position resets, allowing the user to start again entering that letter. This is achieved through changes to the Huffman tree, with the overall effect that every symbol has a ‘dot’ as the final bit of its code, hence escape leaves can be reached by entering only dashes. In Figure 9, we show again the Huffman tree from Figure 3, and the new, modified code tree with escape leaves. Let ‘1’ represent the dot bit and ‘0’ represent the dash bit in the codes. There are three types of subtrees (configurations of parent node and its children) that we must consider: (1) both children are terminal leaf nodes; (2) one child is a leaf node and one child is an internal (non-leaf) node (denoted with a circle in the graph in Figure 9); and (3) both children are internal nodes. The changes to the tree for each case are:
Figure 9.
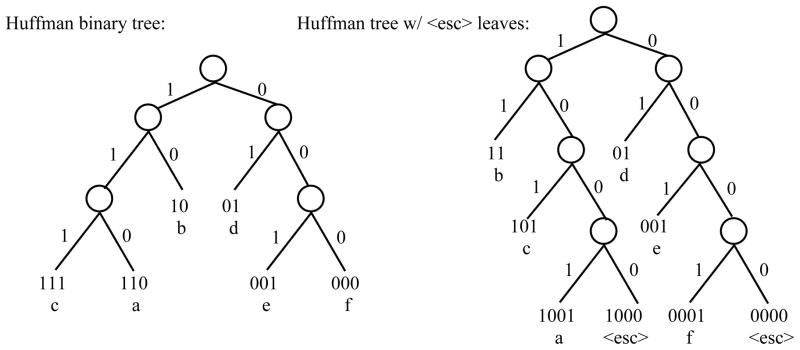
Two binary trees for encoding letters based on letter probabilities: (1) Huffman coding; and (2) Huffman coding with escape leaves.
One leaf and one internal node: For these sub-trees, the leaf node is now always reached with a ‘1’ bit (a dot). For example, consider the symbol ‘b’ in Figure 9, which in the original tree has code ‘10’, but now has code ‘11’.
Two leaf nodes: Without loss of generality, assume that the ‘1’ branch goes to the leaf node with the highest probability. In this case, a new internal node is created, replacing the leaf node reached via the ‘0’ branch. This new internal node then has the leaf node that it replaced as its child, reached along the ‘1’ branch, and an escape leaf as a child along the ‘0’ branch. For example, consider the ‘c’ and ‘a’ leaf nodes on the left corner of the original Huffman coding tree in Figure 9. In the new tree, the ‘a’ symbol is replaced by a new internal node, and hence has an extra bit in its code. This extra bit allows for the inclusion of the escape leaf as the second child of the new node.
Two internal nodes: After the inclusion of all escape nodes as specified above, we ensure that the ‘0’ branch goes to the node with the shortest path to an escape leaf node. In such a way, the path to the nearest escape node is always a series of dashes. In Figure 9, the only part of the tree falling under this condition is at the root of the tree, and both nodes have the same distance path to a leaf node, hence no change is required.
The result of this tree transform is that the code associated with each symbol ends with a dot, hence the user can press dashes until the position is reset. A subset of the symbols will have an extra bit in their code (in this case ‘a’ and ‘f’), though this will typically be the least likely symbols in the vocabulary, hence of limited impact on expected bits. For example, the toy example used in Figures 3 and 9 have expected bits of 2.55 for the original Huffman code and 2.8 bits for the modified code using escape leaves.
In our second alternative, we begin with the new Huffman tree with escape leaves, described above. In addition, we divide the binary code for a given character into a series of frames, each of which displays a maximum of five bits. When the user has entered the five bits for a given frame, and has not specified a complete code for any symbol in the grid, the probabilities for each symbol are re-calculated. Note that this recalculation incorporates the information of the user-entered bits in assigning probability, using the same probability for error as noted in the discussion of Huffman scanning. This can be thought of as a generalization of the error handling of Huffman scanning, where the codes are recalculated after k bits rather than after every bit. From the user’s perspective, the path to resetting the codes after an error is the same as with the previous method (entering dashes instead of dots); but the maximum sequence required to reset is bounded by the number of bits displayed (in this case, 5).
4.4.2. Subjects and Methods
We recruited 13 native English speakers between the ages of 23 and 49 years, seven of whom had participated in our previous text entry experiment but who are not otherwise users of scanning interfaces for text entry, and have typical motor function. Again we used the phrase set from [25] to evaluate text entry performance, using the same five evaluation strings as in the previous experiment. In contrast to the previous experiment, we used an alpha sorted grid – sorted in the order shown in Figure 8 rather than the frequency ordered grid of Figure 4. We chose to use an alpha ordered grid since none of the Huffman coding methods require frequency ordering, and the alpha ordering makes it easier for novices to find their target symbol. In addition, rather than putting users through a calibration phase, we fixed the scan rate for the synchronous methods at 600ms. This choice to eliminate the relatively lengthy calibration phase was made based on our observation that a slightly slower scan rate actually increased overall typing speed of Huffman scanning, since it decreased error and long code rates. Results demonstrated commensurate Huffman scanning text entry speed in these trials as in the prior results.
In lieu of a calibration phase, we provided users with a practice phase in each of the conditions. For this experiment, we tested five keyboard emulation conditions: 1) Row/column auto scan; 2) Synchronous Huffman scanning; 3) Asynchronous Huffman scanning with no reset via escape leaves; 4) Asynchronous Huffman scanning with escape leaves (always requiring a final dot for symbols); and 5) Asynchronous Huffman scanning with escape leaves and recalculating the code after 5 bits.
Subjects were given a brief demo of the five conditions by an author, then proceeded to a practice phase. Practice phrases were given in each of the five conditions, until subjects reached sufficient proficiency in the method to enter a phrase with fewer than 10% errors. After the practice phases in all five conditions were completed, the test phases commenced. The ordering of the conditions in the test phase was random. Subjects again practiced in a condition until they entered a phrase with fewer than 10% errors, and then were presented with the five test strings in that condition. After completion of the test phase for a condition, they were prompted to fill out a short survey about the condition, identical to the survey in the previous experiment.
We used an Ablenet Jellybean® switch as the binary switch, with a short press denoting ‘dot’ and a long press ‘dash’. We used a threshold of 200 ms to distinguish a short versus a long press, i.e., if the button press is released within 200 ms after the press, it is short; otherwise long. As with earlier experiments, to estimate error rates in modeling, we fixed p = 0. 95, i.e., 5% error rate. As before, the task in all conditions was to enter the presented phrase exactly as it is presented. Symbols that are entered in error – as shown in Figure 4 – must be repaired by selecting the delete symbol (←) to delete the incorrect symbol, followed by the correct symbol. The reported times and bits take into account the extra work required to repair errors.
4.4.3. Experimental results
Table 4 presents results from text entry trials in five conditions: row/column auto scanning; synchronous Huffman scanning; and the three variants of asynchronous Huffman scanning (no reset; adding a final dot; and recalculating codes after 5 bits). Unlike previous trials, in this experiment we used an alphabetically sorted grid (as shown in Figure 8). All Huffman scanning trials used the same 8-gram language model as was used in previous experiments, and the scan rate for the two synchronous conditions (row/column and Huffman) was at 600ms.
Table 4.
Text entry results for 13 users on 5 test strings (total 31words, 145 characters) under five conditions, with fixed 600-ms scan rate for the two synchronous conditions.
| Scanning condition | Speed (cpm) mean (std) | Bits per character | Error rate mean (std) | Long code rate mean (std) | ||
|---|---|---|---|---|---|---|
| mean (std) | opt. | |||||
| Row/column auto scan | 15.3 (1.2) | 6.4 (0.5) | 5.6 | 2.9 (2.3) | 6.4 (4.0) | |
| Synchronous Huffman | 25.0 (4.2) | 3.4 (0.8) | 2.6 | 2.2 (1.9) | 8.6 (7.3) | |
| Asynchronous | no reset | 21.3 (3.3) | 2.8 (0.2) | 2.4 | 4.8 (2.3) | 0.0 (0.0) |
| final dot | 22.2 (3.2) | 2.9 (0.2) | 2.5 | 2.7 (1.7) | 1.6 (1.3) | |
| recalc@5 | 19.4 (3.4) | 3.1 (0.3) | 2.5 | 3.4 (2.1) | 5.3 (1.3) | |
From these results we can see a few things. First, the alphabetic sorting and the slower scan rate hurt row/column scanning performance, reducing speed by more than 4 characters per minute compared to our previous experiments, despite reducing error rate and long code rate dramatically. In contrast, synchronous Huff-man scanning was slightly faster than it was when the scan rates were calibrated, due to a reduction in error and long-code rates. Thus the Huffman scanning is going at a more leisurely rate, yet the speed of text entry has increased.
For the asynchronous trials, note that the long-code rate for the ‘no reset’ condition is 0, for the simple reason that any error must result in an erroneously entered symbol. This explains the higher error rate under that condition. While the error recovery strategies for asynchronous text entry reduced the number of errors over the ‘no reset’ condition, this reduction did not translate into dramatically better speed. Further, it is clear from the results that the 5 block recalculation resulted in higher error and long-code rates, and hence should probably be viewed as the dispreferred solution to this problem.
Table 5 shows the results from our subject survey, which again uses a Likert scale for responses. Mean Likert scores are shown in the table. Synchronous Huffman scanning received the highest mean Likert scores for question 3 and the lowest for questions 1, 2 and 4. The error correction methods did not reduce stress or fatigue relative to the ‘no reset’ condition, though again it is clear that the ‘final dot’ method was preferred to the ‘recalc@5’ condition. In general, the asynchronous methods seem to result in higher levels of stress, fatigue, and frustration compared to the synchronous methods.
Table 5.
Mean Likert scores to survey questions (5 = strongly agree; 1 = strongly disagree) for asynchronous trials
| Survey Item | Row/Column | Huffman scanning | Asynchronous | ||
|---|---|---|---|---|---|
| no reset | final dot | recalc@5 | |||
| I was fatigued by the trial | 2.2 | 1.9 | 2.6 | 2.8 | 3.3 |
| I was stressed by the trial | 1.8 | 1.7 | 2.3 | 2.5 | 2.6 |
| I liked this trial | 2.6 | 3.4 | 2.6 | 3.0 | 2.2 |
| I was frustrated by this trial | 1.8 | 1.8 | 2.3 | 2.5 | 3.0 |
One possible reason that additional error recovery strategies were not particularly useful is that in many cases it is less time consuming to just enter a wrong character and then delete it, than to enter enough dashes to reset the code. It is also possible that with three different error-recovery strategies, users might have found it difficult to keep them straight.
Another effect worth considering is that roughly half of the subjects in this study also participated in earlier studies and their experience in previously used conditions might bias their preference. It should also be re-emphasized that the subjects in this sample have no motor impairments and so the physical differences between the methods might have a different effect on results for a motor-impaired population. Further, this study has been focused on novice users, with limited training on the methods; results may differ with expertise, something we did not address in this study.
5. Summary and future directions
We have presented methods for including language modeling in simple fixed-grid scanning interfaces for text entry, and evaluated performance of novice subjects with typical motor control. Our approach includes novel methods that account for errors in a way that allows for subsequent selection of the target symbol. We found that language modeling can make a very large difference in the usability of the Huffman scanning condition. We also found that, despite losing bits to optimal Huffman coding, linear scanning on the grid leads to nearly commensurate text entry speed versus Huffman scanning presumably due to lower processing overhead of scanning and thus fewer mistakes. We found that RSVP was somewhat slower than grid scanning with the same language model and code. Finally, we showed that asynchronous Huffman scanning can be effective for including contextually sensitive language models in fixed grid scanning.
There are several future directions to take this work. First, this paper focused on novice users, and it is unclear what the learning curve would look like for the presented methods. Having individuals use the interface over a longer period of time, and with more naturalistic tasks such as free text entry, is of high interest. Also, use of the system by individuals who are AAC users is important. We have been running experiments with such scanning methods with functionally locked-in subjects, and a paper presenting those results is in preparation.
While we have tested some informative configuration alternations in this paper, we are far from exhausting the possibilities. For example, word completion could be straightforwardly incorporated into this scanning method, and it would be interesting to observe the improvements in typing through such a mechanism. We have also been working on ideas of autocompletion, and new methods for estimating the probability of the delete symbol. We will also examine the impact of language model adaptation to a particular user, which should improve the coding of the system, to the extent that the predictions made by the model are based on actual usage by the user. Finally, we are investigating language modeling methods that are resistant to spelling errors that are left uncorrected by the system user.
This research is part of a program to make the simplest scanning approaches as efficient as possible, so as to facilitate the use of binary switches for individuals with the most severe impairments. Huffman scanning is another method for leveraging statistical models to improve the speed of text entry with AAC devices.
Highlights.
New methods for scanning based on Huffman coding
New methods to incorporate keystroke error into Huffman coding for scanning
Comparison of row/column, linear and Huffman coding methods
Asynchronous scanning methods using Huffman codes
Acknowledgments
This research was supported in part by NIH Grant #1R01DC009834-01 and NSF Grant #IIS-0447214. Any opinions, findings, conclusions or recommendations expressed in this publication are those of the authors and do not necessarily reflect the views of the NSF or NIH.
Appendix A. Scanning as a binary code
In order to compare row/column scanning with Huffman scanning at the algorithm level, we will present a discussion of the approach in terms of assigning a binary code, and pseudocode that makes that concrete. Indirect selection methods such as row/column scanning implicitly assign a binary code to every symbol in the grid. If activating the switch (e.g., pressing a button or blinking) is taken as a ‘yes’ or 1, then its absence is taken as a ‘no’ or 0. In such a way, every letter in a spelling grid has a binary code based on the scanning strategy. For example, in Figure 1(a), the letter ‘n’ is in the third row and fourth column; if row scanning starts at the top, it takes two ‘no’s and a ’yes’ to select the correct row; and then three ‘no’s and a ‘yes’ to select the correct column. This translates to a binary code of ‘0010001’.
A single pass through the grid using row/column scanning can be formalized as the algorithm in Figure A.10. If the algorithm returns (0,0) then nothing has been selected, requiring rescanning. If the function returns (i, 0) for i > 0, then row i has been selected, but columns must be rescanned.
Figure A.10.
Algorithm for row/column scanning on a spelling grid. The function YESSWITCH returns true if the switch is activated (or whatever switch event counts as a ‘yes’ response) within the parameterized dwell time.
A more general scanning algorithm based on binary coding can be achieved by ignoring the position of the symbol in the spelling grid. Rather, we can derive the code using some method (e.g., Huffman coding), then use that code to derive the highlighting of the grid during scanning. First, assign a unique binary code to each symbol in the symbol set V (letters in this case). For each symbol a ∈ V, let |a| denote the number of bits in the code representing the letter. Let a[k] be the kth bit of the code for symbol a. We will assume that no symbol’s binary code is a prefix of another symbol’s binary code. Given such an assignment of binary codes to the symbol set V, the algorithm in Figure A.11 can be used to select the target symbol in a spelling grid.
Figure A.11.
Algorithm for binary code symbol selection
Appendix B. Corpora and text normalization
In this section, we detail the corpora used for training language models used by our systems, as well as text normalization methods used on those corpora.
The New York Times portion of the English Gigaword corpus consists of SGML marked-up articles from the New York Times from 1994 to 2002, totaling approximately 914 million words. Some documents in this collection are near repeats, since updated, extended or edited articles are included in the collection. Most often these are included in series, with repeated titles, allowing for trailing versions to be discarded. Articles with no headline or no dateline were discarded, as were articles that were not identified as type “story”. Tabular articles, such as bestseller lists, were also discarded. All content between paragraph delimiters were placed on a single line (single space replacing existing newline characters within the paragraph), followed by a newline. No sentence segmentation was performed.
An iterative procedure was followed to reduce duplication in the corpus. Repeated strings of length greater than 50 characters were extracted and sorted by count. Some of these were due to common article types, such as book lists, which allowed us to determine criteria for article exclusion. Others were due to meta-data communicating editing requirements to the editors, e.g., “(OPTIONAL TRIM)”. Some of these signaled the end of the article, and any material from that point to the end of the document could be discarded. Others indicated that the article as a whole should be discarded. Once a set of patterns indicating various actions were extracted (e.g., specific header content indicating that the document should be discarded), a new corpus was generated, and the process was repeated, until the repeated substrings stopped yielding any substantial changes to the normalization procedure.
For the Enron Email Dataset, we used data from the SQL database made available by Andrew Fiore and Jeff Heer,5 who performed an extensive amount of duplicate removal and name normalization. Text was extracted from the “bodies” table of the database, which corresponds to the bodies of the email messages. Normalization was similar to the iterative procedure for the New York Times detailed above, in an attempt to limit the amount of spam and mass mailings, as well as to remove pasted signatures and attachments from the end of emails. In contrast to the New York Times data – which consists largely of very short paragraphs – sentence segmentation was performed on the email data, with the newline character used as a sentence delimiter. Again, the intent of the normalization was to have a corpus that is representative of typed text.
Finally, we made use of approximately 112 thousand words from the CMU Pronouncing Dictionary,6 which was appended to each of our corpora to give better word coverage.
For each of our corpora, we de-cased the resulting corpus and selected sentences that only included characters that would appear in our 6×6 spelling grid. Those characters are: the 26 letters of the English alphabet, the space character, a delete symbol, comma, period, double and single quote, dash, dollar sign, colon and semi-colon.
Appendix C. Language modeling methods
In this section, we detail the training methods for language models used in the systems evaluated in this paper. First, we establish some notation.
For a string of symbols W, let W [i, j] be a substring beginning at the ith symbol and ending at the jth symbol, and let Wi = W [i, i] i.e., the ith symbol. An n-gram model is a Markov model of order n−1, which means that it conditions the probability of each symbol Wi on the previous n−1 symbols W [i−n+1, i−1]. Thus a 12-gram model conditions the probability of each symbol Wj on the previous 11 symbols W [i−11, i−1]. For example, if the partial string “we run the ri” has been entered, the probability of the next symbol in a 12-gram model would be conditioned on “ run the ri”, i.e., the final 11 characters in the partial string (including spaces).
The maximum likelihood estimate for these n-gram probabilities is estimated by relative frequency estimation from a corpus. Let f(W [i, j]) denote the frequency of the substring W [i, j] in the training corpus. Then
| (C.1) |
These maximum likelihood models are typically recursively smoothed (or regularized) to lower order n-gram models to derive the final probability estimate, to avoid assigning zero probabilities. For this paper, we use model interpolation with a smoothing parameter 0 ≤ λ ≤ 1, as follows:
| (C.2) |
where λ(W [j, i]) is estimated using the version of Witten-Bell smoothing with hyperparameter K from [8], as follows:
| (C.3) |
The second term in the denominator of Equation C.3 is the hyperparameter K times the size of the set of words that are observed following the string W [j, i] at least once in the corpus. To end the smoothing recursion, we smooth the unigram model (Markov order 0) with a uniform distribution, so that all symbols have probabilities.
For hyper-parameter settings, we used a 100k character development set. Our best performing hyper-parameter for the Witten-Bell smoothing was K=15, which is comparable to optimal settings found in [8] for 12-grams.
Appendix D. Test phrases
The following five phrases from the MacKenzie and Soukoreff [25] collection were used in the testing phase of all experiments reported here:
i can see the rings on saturn
watch out for low flying objects
neither a borrower nor a lender be
an offer you cannot refuse
the facts get in the way
Footnotes
Methods have been explored to include some contextual influence while minimizing the required grid reorganization. See Section 2.1 for background.
Expected code length is the weighted average length of the code, calculated by summing the bits for each symbol multiplied by that symbol’s probability.
In our interface, as in most row/column scanning systems, column scanning highlights only the cell from the selected row, not the entire column.
Counting of n-grams is done using a suffix tree, allowing for arbitrary length n-grams.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Anson D, Moist P, Przywars M, Wells H, Saylor H, Maxime H. The effects of word completion and word prediction on typing rates using on-screen keyboards. Assistive Technology. 2004;18 (2):146–154. doi: 10.1080/10400435.2006.10131913. [DOI] [PubMed] [Google Scholar]
- 2.Baletsa G. Master’s thesis. Tufts New England Medical Center; 1977. Anticipatory communication. [Google Scholar]
- 3.Baletsa G, Foulds R, Crochetiere W. Design parameters of an intelligent communication device. Proceedings of the 29th Annual Conference on Engineering in Medicine and Biology; 1976. p. 371. [Google Scholar]
- 4.Baljko M, Tam A. Indirect text entry using one or two keys. Proceedings of the Eigth International ACM Conference on Assistive Technologies (ASSETS); 2006. pp. 18–25. [Google Scholar]
- 5.Beckley R, Roark B. Asynchronous fixed-grid scanning with dynamic codes. Proceedings of the 2nd Workshop on Speech and Language Processing for Assistive Technologies (SLPAT); 2011. pp. 43–51. [Google Scholar]
- 6.Beukelman D, Mirenda P. Augmentative and Alternative Communication: Supporting children and adults with complex communication needs. 3. Paul H. Brookes; Baltimore, MD: 2005. [Google Scholar]
- 7.Broderick T, MacKay DJC. Fast and flexible selection with a single switch. PLoS ONE. 2009;4 (10):e7481. doi: 10.1371/journal.pone.0007481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Carpenter B. Scaling high-order character language models to gigabytes. Proceedings of the ACL Workshop on Software; 2005. pp. 86–99. [Google Scholar]
- 9.Chen S, Goodman J. An empirical study of smoothing techniques for language modeling, technical Report, TR-10-98. Harvard University; 1998. [Google Scholar]
- 10.Crochetiere W, Foulds R, Sterne R. Computer aided motor communication. Proceedings of the 1974 Conference on Engineering Devices in Rehabilitation; 1974. pp. 1–8. [Google Scholar]
- 11.Darragh J, Witten I, James M. The reactive keyboard: A predictive typing aid. Computer. 1990;23 (11):41–49. [Google Scholar]
- 12.Demasco P. Human factors considerations in the design of language interfaces in AAC. Assistive Technology. 1994;6:10–25. doi: 10.1080/10400435.1994.10132224. [DOI] [PubMed] [Google Scholar]
- 13.Foulds R, Baletsa G, Crochetiere W. The effectiveness of language redundancy in non-verbal communication. Proceedings of the Conference on Devices and Systems for the Disabled; 1975. pp. 82–86. [Google Scholar]
- 14.Foulds R, Soede M, van Balkom H. Statistical disambiguation of multi-character keys applied to reduce motor requirements for augmentative and alternative communication. Augmentative and Alternative Communication. 1987;3 (4):192–195. [Google Scholar]
- 15.Grover D, King M, Kushler C. US Patent # 5818437 Reduced keyboard disambiguating computer. 1998
- 16.Heckathorne C, Voda J, Liebowitz L. Design rationale and evaluation of the portable anticipatory communication aid – PACA. Augmentative and Alternative Communication. 1987;3 (4):170–180. [Google Scholar]
- 17.Huffman D. A method for the construction of minimum redundancy codes. Proceedings of the IRE; 1952. pp. 1098–1101. [Google Scholar]
- 18.Kneser R, Ney H. Improved backing-off for m-gram language modeling. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP); 1995. pp. 181–184. [Google Scholar]
- 19.Kurtz I, Treviranus J. US Patent # 5608395 Simplified computer access system. 1997
- 20.Lesher G, Moulton B, Higginbotham D. Optimal character arrangements for ambiguous keyboards. IEEE Transactions on Rehabilitation Engineering. 1998;6:415423. doi: 10.1109/86.736156. [DOI] [PubMed] [Google Scholar]
- 21.Lesher G, Moulton B, Higginbotham D. Techniques for augmenting scanning communication. Augmentative and Alternative Communication. 1998;14:81–101. [Google Scholar]
- 22.Levine SH, Goodenough-Trepagnier C, Getschow CO, Minneman SL. Multi-character key text entry using computer disambiguation. Proceedings of the 10th Annual Conference on Rehabilitation Engineering (RESNA); 1987. pp. 177–179. [Google Scholar]
- 23.Li J, Hirst G. Semantic knowledge in word completion. Proceedings of the 7th International ACM Conference on Computers and Accessibility.2005. [Google Scholar]
- 24.MacKay D, Ball C, Donegan M. Efficient communication with one or two buttons. In: Fischer R, Preuss R, von Toussaint U, editors. Maximum Entropy and Bayesian Methods, v.735 of AIP Conference Proceedings. American Institute of Physics; Melville, NY, USA: 2004. pp. 207–218. [Google Scholar]
- 25.MacKenzie I, Soukoreff R. Phrase sets for evaluating text entry techniques. Proceedings of the ACM Conference on Human Factors in Computing Systems (CHI); 2003. pp. 754–755. [Google Scholar]
- 26.Nantais T, Shein F, Treviranus J. A predictive selection technique for single-digit typing with a visual keyboard. IEEE Transactions on Rehabilitation Engineering. 1994;2 (3):130–136. [Google Scholar]
- 27.Perelmouter J, Birbaumer N. A binary spelling interface with random errors. IEEE Transactions on Rehabilitation Engineering. 2000;8 (2):227–232. doi: 10.1109/86.847824. [DOI] [PubMed] [Google Scholar]
- 28.Roark B, de Villiers J, Gibbons C, Fried-Oken M. Scanning methods and language modeling for binary switch typing. Proceedings of the NAACL-HLT Workshop on Speech and Language Processing for Assistive Technologies (SLPAT); 2010. pp. 28–36. [Google Scholar]
- 29.Schadle I. Sibyl: AAC system using NLP techniques. Proceedings of the 9th International Conference on Computers Helping People with Special needs (ICCHP); 2004. pp. 1109–1015. [Google Scholar]
- 30.Shannon C. Prediction and entropy of printed English. Bell System Technical Journal. 1950;30:50–64. [Google Scholar]
- 31.Trnka K, Yarrington D, McCaw J, McCoy K, Pennington C. The effects of word prediction on communication rate for AAC. Proceedings of HLT-NAACL; Companion Volume, Short Papers; 2007. pp. 173–176. [Google Scholar]
- 32.Trnka K, Yarrington D, McCoy K, Pennington C. Topic modeling in fringe word prediction for AAC. Proceedings of the International Conference on Intelligent User Interfaces; 2006. pp. 276–278. [Google Scholar]
- 33.Trost H, Matiasek J, Baroni M. The language component of the FASTY text prediction system. Applied Artificial Intelligence. 2005;19 (8):743–781. [Google Scholar]
- 34.Wandmacher T, Antoine J. Methods to integrate a language model with semantic information for a word prediction component. Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP); 2007. pp. 506–513. [Google Scholar]
- 35.Wandmacher T, Antoine J, Poirier F, Departe J. Sibylle, an assistive communication system adapting to the context and its user. ACM Transactions on Accessible Computing (TACCESS) 2008;16(1):1–30. [Google Scholar]
- 36.Ward D, Blackwell A, MacKay D. DASHER – a data entry interface using continuous gestures and language models. Human-Computer Interaction. 2002;17 (2–3):199–228. [Google Scholar]
- 37.Witten I, Bell T. The zero-frequency problem: Estimating the probabilities of novel events in adaptive text compression. IEEE Transactions on Information Theory. 1991;37 (4):1085–1094. [Google Scholar]