Table 5. Response surface regression results and their F values at the four different elevations and the composite site.

Site	A00	A01	A02	A10	A11	A20	F	F0.01(5,49)/F0.01(5,48)
H	0.142/−0.1	−0.264/0.163	−0.216/0.149	0.866/0.6	0.573/0.022	−0.259/−0.047	8.8/7.4**	3.42/3.43
MH	0.116/−0.081	0.025/0.189	−0.12/0.129	0.863/0.67	0.496/0.022	−0.284/−0.046	19.1/10.7**	3.42/3.43
ML	0.128/−0.025	0.018/0.156	−0.121/0.097	0.761/0.608	0.315/0.004	−0.19/−0.071	10.2/7.3**	3.42/3.43
L	0.328/−0.115	−0.278/0.12	−0.227/0.163	0.917/0.626	0.351/0.081	−0.309/−0.045	8.9/9.3**	3.42/3.43
All	0.199/−0.09	−0.148/0.16	−0.181/0.141	0.901/0.638	0.461/0.037	−0.287/−0.049	11.8/9.2**	3.42/3.43

The response surface was defined by a quadratic surface function: .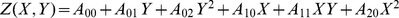

Here, Z = Z score value of standardized tree ring index at different elevations and the whole site; X = Z score value of mean precipitation (previous July to current June); Y = Z score value of mean temperature (previous September to current March). The F value is calculated by 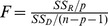, with notation as follows. 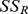: regression sum of squares, 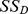: residual sum of squares, p: degrees of freedom of the regression function, here p = 5, n: number of active data, here n = 55. If 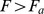, the response surface regression is significant at the α level.

^**F value is significant at p = 0.01 level.