Henle fiber layer phase retardation measured with polarization-sensitive optical coherence tomography

Abstract

Abstract: We developed a method based on polarization-sensitive optical coherence tomography (PS-OCT) to quantify the double pass phase retardation (DPPR) induced by Henle fiber layer in three subjects. Measurements of the retina were performed at a mean wavelength of 840 nm using two polarization states that were perpendicular in a Poincaré sphere representation and phase retardation contributions from tissue layers above and below the Henle fiber layer were excluded using appropriately placed reference and measurement points. These points were semi-automatically segmented from intensity data. Using a new algorithm to determine DPPR, the Henle fiber layer in three healthy subjects aged 50-60 years showed elevated DPPR in a concentric ring about the fovea, with an average maximum DPPR for the three subjects of 22.0° (range: 20.4° to 23.0°) occurring at an average retinal eccentricity of 1.8° (range: 1.5° to 2.25°). Outside the ring, a floor of approximately 6.8° was measured, which we show can mainly be attributed to phase noise that is induced in the polarization states. We also demonstrate the method can determine fast axis orientation of the retardation, which is found consistent with the known radial pattern of Henle fibers.

1. Introduction

The structured organization of the Henle fiber layer (HFL) is well known to exhibit birefringence, a difference in refractive index experienced by light polarized perpendicular and parallel to the direction of the fibers [1]. Aging and macular diseases such as age-related macular degeneration and diabetic retinopathy are known to disrupt the organization of these fibers and reduce layer birefringence [2, 3]. Since disruption indicates structural changes to otherwise well-ordered neural tissues, birefringence measurements may serve as a sensitive indicator of disease onset. To investigate these possibilities, we have developed a method based on polarization-sensitive optical coherence tomography (PS-OCT) to measure the retardation induced by HFL. To demonstrate the capabilities of the method, detailed measurements of the double pass phase retardation (DPPR) induced by HFL in three clinically normal subjects are presented.

Unlike other polarization measurement methods that have been applied to HFL, including two based on PS-OCT [4, 5], our method axially separates the birefringence contribution of the HFL from that of the other retinal and ocular layers, and laterally resolves its distribution on an absolute scale. Our method makes no assumptions about the uniformity and linearity of the anterior segment retardance nor that of the HFL.

In our previous PS-OCT work, we determined DPPR per unit depth of the retinal nerve fiber layer (RNFL) by fitting spatially averaged DPPR data with least squares [6–9]. A similar analysis was followed by Yamanari et al [10]. Kemp et al. and Dwelle et al. fitted RNFL DPPR data in the Poincaré sphere [11, 12]. Using an open air PS-OCT system without single mode fiber and an input state that was circularly polarized, Götzinger et al. determined the birefringence induced by the RNFL by fitting DPPR data with a linear regression method [13]. They used a histogram of DPPR data obtained near the photoreceptors to determine the maximum DPPR induced by the RNFL. Zotter et al. used a similar approach, but did not perform any spatial averaging [14]. A novelty in our paper is that measurements at only two depths are used to determine the phase retardation that is induced by the HFL. A reference measurement is acquired above HFL (below the RNFL), while the retardation induced by the HFL is recorded at the interface between the inner and outer segments of the photoreceptor layer.

2. Method

Phase retardation measurements were performed with a spectral-domain PS-OCT system with a Wollaston prism in the spectrometer, designed after Cense et al [9]. In comparison to the previous design, the Wollaston prism was positioned between the collimator and the grating, so that a smaller sized and therefore less expensive Wollaston prism could be used [15]. The instrument records depth-resolved intensity and birefringence simultaneously. By modulating the input polarization state 90° in a Poincaré sphere representation in adjacent A-scans, system birefringence and ocular birefringence up to the layer of interest in the retina are removed [16]. This detection scheme therefore facilitates quantification of phase retardation in layers of interest without contamination of retardation contributions or noise from other retinal layers, provided that there is minimal diattenuation present. Furthermore, the method ensures that even in the extreme case when the polarization state in one A-scan exactly aligns with the fast axis or slow axis of the tissue, the polarization state in the other remains sensitive to the tissue retardation [17]. After the phase retardation in each A-scan is determined, the two measurements are angle- and intensity-weighted, which accounts for angular differences between the fast axis and individual polarization states as well as reflectance differences. This ensures that the larger weight is given to the more accurate measurement, with the result being that the final retardation measurement is insensitive to the incident polarization states [17].

In earlier PS-OCT work, a similar method was used to measure RNFL retardation, and in those measurements the retinal surface was used as a reference [6–9]. A novelty in this study is that with proper segmentation the reference was chosen below the RNFL to avoid contamination by RNFL retardation. Also in the previous RNFL work, DPPR data were fit using least squares to determine the DPPR per unit depth. For HFL, this approach is likely unreliable as the HFL reflects substantially less light than the RNFL (HFL appears between one and two orders of magnitude (~10-20 dB) dimmer than the RNFL) leading to poor signal to noise ratio. To avoid this, we sampled the polarization state of the light after it passed through HFL using the bright reflectance from the interface between the inner and outer segments of the photoreceptors (IS/OS). This approach took advantage of the fact that tissue between HFL and the IS/OS is not birefringent. We found IS/OS to be sufficiently separated from the retinal pigment epithelium (RPE) that its Stokes vectors are not corrupted by the strong phase scrambling measured at the RPE [18].

Three subjects with no history of ocular disease (age: 50, 55, and 60 years) were recruited from the Indiana University School of Optometry. Measurements adhered to the tenets of the declaration of Helsinki. After informed consent, PS-OCT images were acquired of one eye of each subject without mydriasis or cycloplegia. A Badal optometer corrected for defocus to maximize signal in the OCT images. The lateral resolution of the instrument was estimated at approximately 20 μm (full width at half maximum). It has been recently shown that the reflectance of HFL is sensitive to the incident angle of the imaging beam owing to variations in the orientation of Henle fibers [19]. For the DPPR measurement we erred on the conservative side and avoided the angle effect altogether. This was accomplished by positioning the beam in the entrance pupil such that A-scans were always oriented perpendicular to the photoreceptor layer. The input power was kept below 600 μW, which is eye safe according to ANSI safety standards [20].

Volumetric scans (15° × 15°; 100 × 1000 A-scans) centered on the fovea were recorded at an A-scan rate of 25 kHz. The measurement time for data acquisition of one volume was 4.4 s. The axial resolution of the PS-OCT system was quantified as 5.9 μm (full width at half maximum) in tissue (n = 1.38). The IS/OS boundary was segmented using a semi-automatic layer detection algorithm that required the operator to locate the IS/OS in the first A-scan of each B-scan. The IS/OS boundary was then used in combination with a cross-correlation algorithm to realign adjacent B-scans with each other, to remove axial motion artifacts. The reference position for DPPR determination was offset a fixed distance anteriorly from the IS/OS, specified to be the retinal thickness at the bottom of the fovea pit. This assured that the reference position stayed well below the RNFL. This offset was optimized for each subject. The two orthogonally polarized spectra recorded with the polarization-sensitive spectrometer were processed into Stokes vectors for DPPR calculations, i.e. for each pixel a full set of Stokes parameters was determined [16]. The Stokes vectors were averaged over 5 pixels (18.5 μm) in depth and 7 pixels (31.5 μm) in width, since speckle is a source of phase noise that degrades the stability of the phase retardation measurement. Moreover, since the reference is located in less well-reflecting tissue, the Stokes vectors at the reference of all 500 odd and 500 even A-lines were averaged to improve the Stokes vector accuracy. A comparison of analyzed DPPR data with and without Stokes vector averaging of all reference points showed similar HFL DPPR magnitude, with the data without the averaging having a larger background noise.

Uncertainty in the orientation of the measured polarization state is related to the signal-to-noise ratio (SNR) of the corresponding intensity image. Specifically, the standard deviation in the orientation of the measured polarization state is

$$\text{Δθ}=\sqrt{\frac{\text{2}}{\text{SNR}}}=\sqrt{\frac{\text{2}}{\left(\frac{\text{I}}{{\text{SD}}_{\text{noise}}}\right)}}$$ (1)

with Δθ in radians, I the intensity and SD_noise the standard deviation in the noise [21]. Note that the linear intensity I is used in Eq. (1). The SNR was determined by dividing the linear intensity of each pixel (I) by the standard deviation in intensity over a subgroup of pixels at a location with no signal (SD_noise). Using this SNR definition, Δθ was calculated for all pixels in the DPPR B-scan [21].

Data were post-processed to extract DPPR data along vertical and horizontal meridians bisecting the foveal center. The distribution of DPPR indicated circumferential symmetry, and to compare data obtained from different subjects, DPPR data were averaged to show the effect of retinal eccentricity, ignoring potential circumferential differences, referred to as circumferential averaging. Data points at the same radial distance from the foveal center were averaged. The standard deviation was also determined.

As a final step, we calculated the fast axis orientation of HFL for one of the subjects. We used the same Stokes vectors, and reference and IS/OS planes as for the DPPR calculations [21]. The fast axis was calculated across the 15° × 15° volumetric scan and plotted in a Poincaré sphere representation.

3. DPPR results

Figure 1 shows a representative logarithmic intensity and processed DPPR B-scan from the 55-year old subject. For each pair of A-scans, the DPPR between the reference pixel (upper red dashed line) and the other pixels in the A-scan pair was computed, yielding an image as shown in panel B of Fig. 1. The measurement location at the IS/OS (lower red dashed line) was then used to determine the DPPR induced by HFL. Without noise, DPPR accumulates with depth in birefringent tissue. Speckle and shot noise, however, can cause variations in DPPR as a function of depth, causing the DPPR to randomly increase and decrease. These variations can be minimized by using a larger kernel for spatial averaging, but a larger kernel size may average in data points of tissue with a lower or higher birefringence. Using the averaged SNR data, the DPPR data were masked and pixels with a polarization state with a standard deviation, Δθ, larger than 4° were colored gray (Fig. 1(B)) and removed from further processing. Here we incorporated the fact that the DPPR calculation is performed using speckle averaged data that are averaged over a kernel of 35 points, reducing the effective standard deviation of each of the pixels by a factor of √35 or 5.9 times.

Fig. 1.

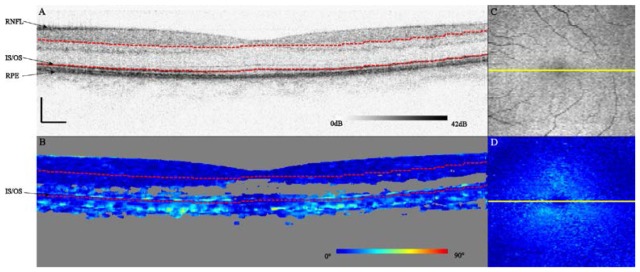
Logarithmic intensity (A) and DPPR (B) B-scans centered on the fovea of the right eye of a 55-year old subject. Scale bars represent a length of 250 μm. Pixels with an effective standard deviation in the orientation of the polarization state larger than 4° were colored gray. On the right, an en face intensity C-scan obtained at the IS/OS (C) and DPPR C-scan (D) are shown. The location of the B-scan is marked by a yellow line. Red dashed lines in the B-scans indicate the reference and measurement locations for the DPPR calculation. While the DPPR data were averaged to reduce the influence of noise, the intensity data (A,C) were not. This link shows a movie of all 100 B-scans (Media 1 ^{(9MB, AVI)} ).

Applying the DPPR calculation to the 100 B-scans that form each volume, the DPPR induced by HFL can be visualized as an en face C-scan (Fig. 1(D)), in this case showing the characteristic “donut” or annular shape of phase retardation results expected for radially-oriented photoreceptor axons in the macula (HFL). Low DPPR is observed in the center and periphery of the macula, consistent with the thinner HFL and more vertically oriented photoreceptor axons at these locations. The latter is important because of the absence of retardation along the axon length.

For a quantification of DPPR, horizontal and vertical slices bisecting the fovea center (Fig. 2(B) ) and a circumferential average (Fig. 2(C)) were made. The horizontal and vertical slices show similar patterns, with minima in the center and edges. The minimum DPPR measured was approximately 5°, which occurred near the center. The standard deviation in Fig. 2(C) was determined from the averaged data points at each radius.

Fig. 2.

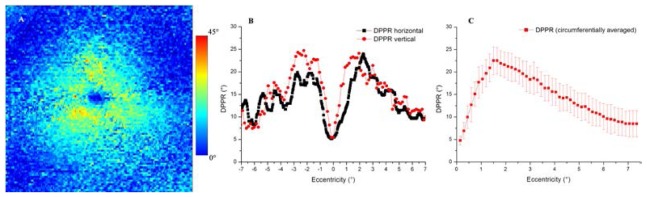
(A) DPPR induced by HFL in the right eye of a 55-year old male subject, color encoded over 45 degrees. The image measures 15° by 15°. (B) DPPR traces are of horizontal and vertical scans that bisect the foveal center. (C) Circumferential average of the en face DPPR map in (A). Error bars represent one standard deviation of the circumferential trace.

To facilitate a comparison of the main distribution features of DPPR among the three subjects and to previously reported results, circumferential averages were made, similar to Fig. 2(C). Figure 3 shows DPPR images and DPPR graphs of the other two subjects.

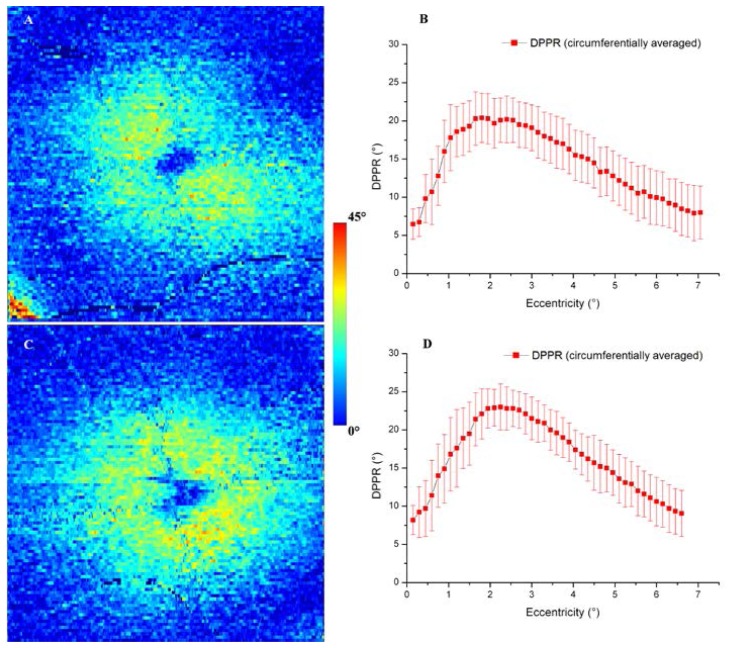
Fig. 3.

(A) DPPR induced by HFL in the right eye of a 60-year old female subject, color coded over 45 degrees. (B) Circumferential average of the DPPR map in (A). Similar results are shown for the left eye of a 50-year old female (C, D). Error bars represent one standard deviation of the circumferential trace. Note the elevated DPPR in the lower left corner of the map in (A) due to the birefringent RNFL. This subject had a relatively thick RNFL and large blood vessel at this location that together caused the reference (which was chosen using a fixed offset to the location of the IS/OS) to intersect the RNFL. While the resulting DPPR is high, the corner falls outside the circumferential average window (<7.5° retinal eccentricity) that was used for processing.

As shown in Figs. 2 and 3, all three subjects exhibited the characteristic cross-sectional profile expected of radially oriented Henle fibers: a DPPR minimum near 0° eccentricity, a steep monotonic increase over the first couple degrees of eccentricity, and a shallow monotonic decrease out to the edge of the measurement window (7.5° eccentricity). Average maximum DPPR for the three subjects is 22.0° (range: 20.4° to 23.0°) occurring at an average retinal eccentricity of 1.8° (range: 1.5° to 2.25°).

4. Comparison to HFL measurements in literature

In a recent study, Twietmeyer et al. measured the DPPR of a 15° × 15° patch centered on the macula in 15 subjects at 780 nm using a Mueller-matrix polarimeter. The polarimeter was based on modifications to a commercially available GDx polarimeter (Laser Diagnostic Technologies) [22]. Averaging the DPPR maps across all subjects, they report a maximum DPPR value of 21.1°. Our average maximum 22.0° (range: 20.4° to 23.0°) across three subjects is consistent with this. An added benefit of our PS-OCT method is the inclusion of a circumferential average that takes advantage of the HFL radial symmetry. The error bars (DPPR standard deviations) in the plots of Figs. 2 and 3 indeed reveal substantial variations across the DPPR annular pattern. For example across the three subjects, the average DPPR standard deviation at the maximum DPPR value is 2.8°. Taking into account the 7 pixel (31.5 μm) lateral averaging of Stokes vectors used in our processing, we estimate conservatively 108 independent samples along the circumference of the annular pattern where maximum DPPR occurs (average retinal eccentricity of 1.8°). Standard error of the circumferentially averaged DPPR is then 2.8°/sqrt(108) = 0.27°. Thus inclusion of more measurements in this way noticeably improves the method’s precision and ability to discern DPPR differences between subjects.

Another benefit of our PS-OCT method is that the birefringence contribution of HFL can be precisely targeted. In this study we chose for convenience to place the reference at a fixed distance from the IS/OS anterior of HFL. However, there appears to be considerable flexibility in reference position. As an example of this in one subject, we systematically repositioned the reference at increments of 15 µm, starting immediately posterior of RNFL and ending near HFL. DPPR maps were reconstructed and circumferential averages generated for each. All yielded similar DPPR profiles (< 1 degree difference), strongly indicating that the source of the birefringence we detected indeed originates from HFL and that the layers between HFL and the RNFL contribute negligibly. A third benefit is that our method explicitly bypasses the corneal component by placement of the reference within the retina. In contrast in the previous study with the Mueller-matrix polarimeter, only three of 15 subjects had well-defined annular-like patterns for HFL retardance. The authors suggested this was likely due to incomplete compensation of corneal birefringence using their method.

The retinal eccentricity at which maximum DPPR occurs in our study roughly approximates that in an earlier study of 120 clinically normal eyes (1.27° ± 0.29°; age: 50-60 years) [3]. In that study, normalized, but not absolute DPPR was measured with a confocal scanning laser polarimeter (GDx, Carl Zeiss Meditec) in conjunction with Fourier analysis to separate the contribution of HFL from that of the retinal nerve fiber layer. Both methods show a declining HFL retardation eccentric from 2° to 3°, and neither method shows a large contribution eccentric to 5°. A comparison of measurements of these two methods on a broader range of same subjects would be of interest.

5. Noise analysis

Photoreceptor axons are known to be oriented nearly vertical at the foveal center and in the peripheral macula near the edge of the measurement window [19, 23]. This property of the axons coupled with the relatively small thickness of HFL at these locations suggests very low DPPR values. In contrast, the PS-OCT measurements show DPPR values of approximately 5° to 10°. To investigate this apparent discrepancy, we developed an error propagation analysis that extends the DPPR theoretical development by Park et al [17].

As described in the Method section, the standard deviation in the uncertainty of the polarization state is inversely related to the SNR. The DPPR itself is calculated from four measurements in two adjacent A-scans, obtained with two input polarization states that are orthogonal in the Poincaré sphere, and also involves an intensity weighted calculation that takes the angle between the fast axis and individual polarization states in consideration (see Eq. (1) [16, 17]. Since this calculation requires measurements at the reference (anterior of HFL) and IS/OS, the standard deviation at the reference, σ_θref and the standard deviation at the location of the IS/OS (σ_θIS/OS) are of interest. While all Stokes vectors have been speckle averaged in width by a factor of 7, the reference Stokes vectors have been averaged over all 500 A-scans. To account for this additional averaging that will decrease σ_θref, we include a factor of 1/√(500/7) in our estimate. Per even and odd A-scan the standard deviation σ_θ is determined using √(σ_θref ² + σ_θIS/OS ²). This results in a standard deviation for odd A-scans (σ_θ1) and even A-scans (σ_θ2). These will later be used for the calculation of the standard deviation in the DPPR.

Park et al. derived an expression for DPPR given as [17]:

$$\text{DPPR}=\frac{\left({\text{I}}_{\text{1}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{1}}}\right){\text{I}}_{\text{1}}^{\text{'}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{1}}^{\text{'}}}\right)\right){\text{θ}}_{\text{1}}+\left({\text{I}}_{\text{2}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{2}}}\right){\text{I}}_{\text{2}}^{\text{'}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{2}}^{\text{'}}}\right)\right){\text{θ}}_{\text{2}}}{\left({\text{I}}_{\text{1}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{1}}}\right){\text{I}}_{\text{1}}^{\text{'}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{1}}^{\text{'}}}\right)\right)+\left({\text{I}}_{\text{2}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{2}}}\right){\text{I}}_{\text{2}}^{\text{'}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{2}}^{\text{'}}}\right)\right)}$$ (2)

with I₁ and I₁’ the intensity at the reference and IS/OS, respectively, in the odd A-lines, and I₂ and I₂’ in the even A-lines. ${\text{θ}}_{{\text{A,I}}_{\text{1,2}}}$ and ${\text{θ}}_{{\text{A,I}}_{\text{1,2}}^{\text{'}}}$are the angles between the fast axis of the tissue (HFL) and the four measured polarization states. θ₁ and θ₂ are the rotation angles in the Poincaré sphere, obtained with odd and even input states, respectively (see Fig. 4 ). While the standard deviations σ_θ1 and σ_θ2 of the rotation angles θ₁ and θ₂ will have an affect on the angles between the fast axis and the four measured polarization states, these will be ignored as their magnitude is very small compared to the rotation angles involved. σ_θ1 and σ_θ2 were calculated from the SNR at the location of the reference and IS/OS, respectively, using Eq. (1). Applying error propagation theory [24] on Eq. (2) the following equation for the standard deviation in the DPPR is obtained:

Fig. 4.

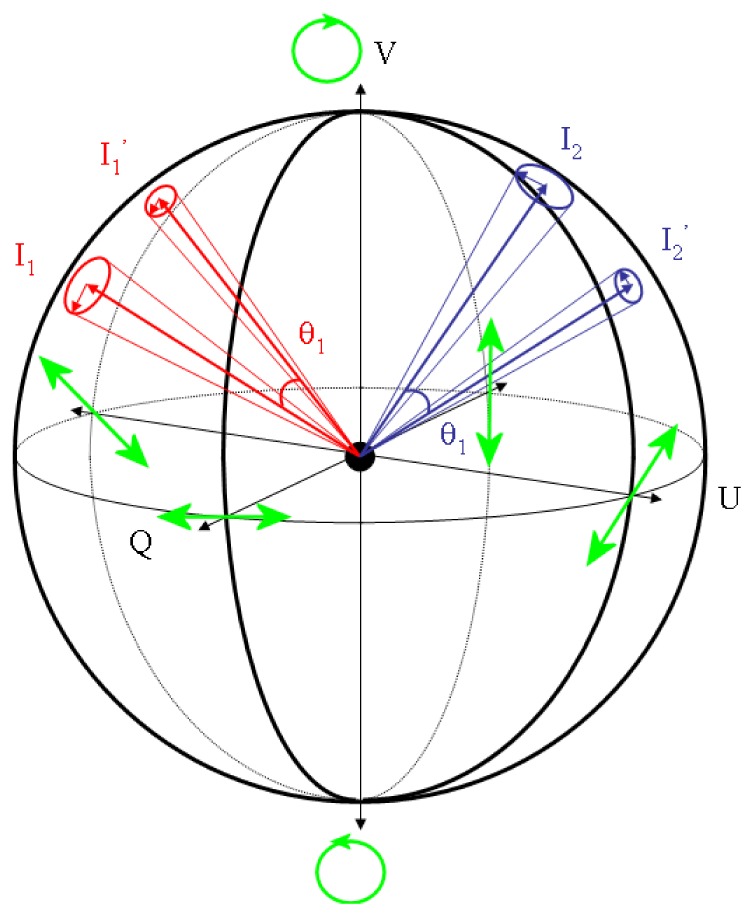
Poincaré sphere with fast axis of HFL oriented towards the reader, depicted by the black dot in the center of the sphere [17]. Both polarization states of the PS-OCT system (red, blue) are shown at two depths and trace out arcs around the fast axis. Arc angles θ₁ and θ₂ are used to calculate DPPR (see Eq. (2). Polarization states at the reference (I₁ and I₂) are shown noisier (larger Δθ) than states at the IS/OS (I₁ ^’ and I₂ ^’) to reflect the lower SNR. Lower SNR increases the standard deviation in the phase retardation measurement, which we derive here using error propagation. For reference, the polarization states at Q, U, V equal to +/− 1 are shown in green.

$$\begin{array}{l}{\text{σ}}_{\text{DPPR}}\text{}=\sqrt{{\left(\frac{\partial \text{DPPR}}{\partial {\text{θ}}_{\text{1}}}\right)}^{\text{2}}\cdot {\text{σ}}_{\text{θ}}{}_{\text{1}}^{\text{2}}+{\left(\frac{\partial \text{DPPR}}{\partial {\text{θ}}_{\text{2}}}\right)}^{\text{2}}\cdot {\text{σ}}_{\text{θ}}{}_{\text{2}}^{\text{2}}}\\ =\sqrt{\begin{array}{l}{\left(\frac{\left({\text{I}}_{\text{1}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{1}}}\right){\text{I}}_{\text{1}}^{\text{'}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{1}}^{\text{'}}}\right)\right)}{\left({\text{I}}_{\text{1}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{1}}}\right){\text{I}}_{\text{1}}^{\text{'}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{1}}^{\text{'}}}\right)\right)+\left({\text{I}}_{\text{2}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{2}}}\right){\text{I}}_{\text{2}}^{\text{'}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{2}}^{\text{'}}}\right)\right)}\right)}^{\text{2}}\cdot {\text{σ}}_{\text{θ1}}{}^{\text{2}}\cdot \cdot \cdot \\ \text{+}{\left(\frac{\left({\text{I}}_{\text{2}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{2}}}\right){\text{I}}_{\text{2}}^{\text{'}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{2}}^{\text{'}}}\right)\right)}{\left({\text{I}}_{\text{1}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{1}}}\right){\text{I}}_{\text{1}}^{\text{'}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{1}}^{\text{'}}}\right)\right)+\left({\text{I}}_{\text{2}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{2}}}\right){\text{I}}_{\text{2}}^{\text{'}}\text{sin}\left({\text{θ}}_{{\text{A,I}}_{\text{2}}^{\text{'}}}\right)\right)}\right)}^{\text{2}}\cdot {\text{σ}}_{\text{θ2}}{}^{\text{2}}\end{array}}\end{array}$$ (3)

σ_DPPR at the depth of the IS/OS can then be plotted and compared to the DPPR measurements (see Fig. 5 ).

Fig. 5.

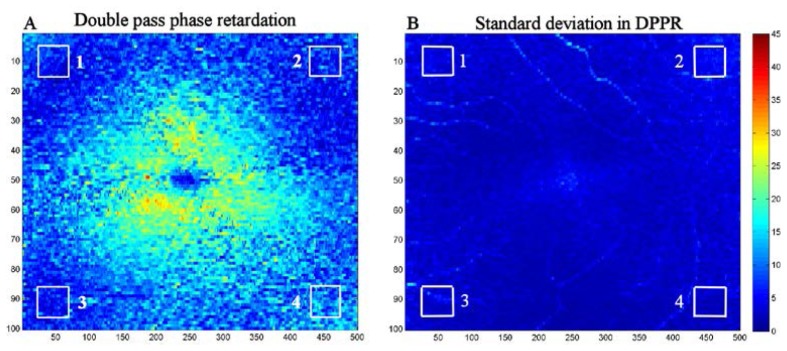
Double pass phase retardation induced by HFL (A), and standard deviation in the DPPR (B), both displayed in the same color coding over 45°. Subject is the 55-year old male (see Figs. 1 and 2). The standard deviation in DPPR was determined from the intensity and DPPR data, using Eq. (3). The four boxes located in the extreme regions of the DPPR and standard deviation maps were analyzed to determine if the DPPR values there are dominated by measurement noise. Averaged over the four boxes in (A) and (B), the mean of the DPPR and the mean of the standard deviation of the DPPR are 7° and 4°, respectively. Note that the DPPR of box 4 (11°) for this subject is considerably higher than the average DPPR of the other boxes (6°) as well as the DPPR values of the other two subjects (see Table 1), indicating that this data point may be an outlier.

Fig. 5(A) shows the measured DPPR induced by the HFL. At the edges of the 15° by 15° scan, the retardation drops. Based on the expected orientation of the photoreceptor axons in the corners, their contribution should be low to the overall DPPR. Instead, we find values that are substantially higher than 0°. Averaged over all four boxes in Fig. 5(A), a mean DPPR value of 7° is found. Fig. 5(B) shows that a large contribution to this number can be attributed to a noise floor created by the standard deviation. Averaged over the same four boxes (this time in Fig. 5(B)) a mean standard deviation of 4° is found.

Similar results were obtained from the other two subjects (see Table 1 ). The maximum SNR in subject A was approximately 46 dB, while the maximum SNR found in subject B and C were 34 dB and 39 dB, respectively. Despite these differences in SNR, the mean DPPR and standard deviation in DPPR in the corners remained strongly correlated with each other (R² = 0.62, p<0.01, with exclusion of the outlier data point of subject A in box 4 of Fig. 5), demonstrating the validity of the method. Averaged over all subjects and all boxes, a mean DPPR of 6.8° and standard deviation of 5.2° were found, demonstrating that the non-zero values in DPPR are consistent with what we expect from the effects of shot noise on the DPPR calculation in tissue without birefringence.

Table 1. Measured mean DPPR and standard deviation in DPPR obtained with Eq. (3) .

	Mean DPPR and σDPPR (°)
Subject	Box 1	Box 2	Box 3	Box 4
A, 55-year old male (OD)	6, 4	7, 5	6, 3	11, 3
B, 60-year old female (OD)	8, 9	7, 4	10, 10	6, 7
C, 50-year old female (OS)	5, 4	5, 5	6, 4	5, 4

The noise analysis of Table 1 indicates a noise floor at around 5.2°, while the circumferentially-averaged values of Figs. 2 and 3 exceed this, e.g., minimum around 8-10° except for at the foveal center. This indicates that the circumferentially-averaged values in the peripheral macula represent real signal and that HFL axons remain obliquely oriented as far out as the edge of the measurement window (7.5°) for these 3 subjects.

Note that in birefringent tissue where the rotation angles θ₁ and θ₂ are large, the standard deviation in DPPR (σ_DPPR) due to shot noise will sometimes lead to an overestimation, and sometimes to an underestimation of the rotation angle. Collectively, these will average out over a large number of data points. A similar scenario does not occur in non-birefringent tissue. Here, shot noise generates only positive rotations for θ₁ and θ_2, and the resulting σ_DPPR always leads to an overestimation of DPPR, as predicted by the use of Eq. (1) and Eq. (3). As a result, DPPR measurements of low birefringent tissue may disappear in the noise floor set by σ_DPPR. This can complicate determining the precise retinal eccentricity at which HFL birefringence reaches a minimum. Of course PS-OCT measurements with higher SNR, for instance by averaging data sets [25] as in the circumferential averages in Figs. 2 and 3, will reduce noise and increase sensitivity to DPPR.

6. Fast axis orientation

While this study focused on measuring the magnitude of the HFL phase retardation, measuring its orientation is also possible with the presented PS-OCT method. To demonstrate this, we calculated the fast axis orientation using the same Stokes vectors, and reference and IS/OS planes as for the DPPR calculations for the 55 year old subject (see Fig. 2). Fast axis measurements across the 15° by 15° image were found to form a concentrated ring of axis orientations in the Poincaré sphere. While the fast axis should be confined to the QU-plane (linear polarization of any orientation), the ring we measured was still crossing the center but rotated off this plane due to birefringence in the PS-OCT fiber and anterior optics of the eye. We corrected for this offset by rotating the ring back onto the QU-plane, the result of which is shown in Fig. 6 .

Fig. 6.

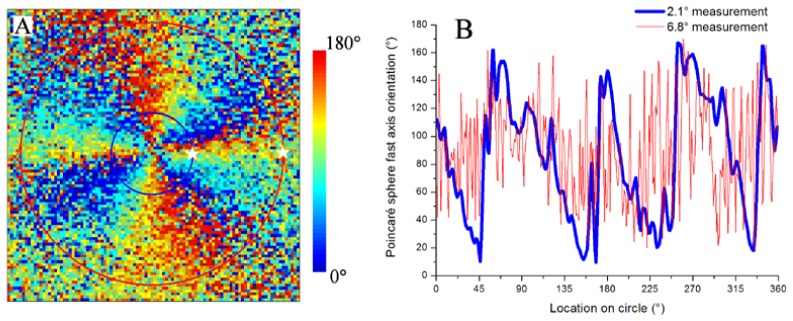
Fast axis orientation of HFL in the right eye of a 55-year old male subject. Axis orientation map is 15° by 15°, and angles are represented on the QU-plane of the Poincaré sphere (A). Color is encoded over 180 degrees, limited by the π-ambiguity of the PS-OCT method. Axis orientation is plotted for circular traces at 2.1° (blue) and 6.8° (red) retinal eccentricities (B), starting at the white stars going anti-clockwise (A). Concentric circles in (A) are color coded to the traces in (B). DPPR results for the same subject are shown in Fig. 2.

The figure shows that the fast axis orientation for this subject is highly sensitive to angular position about the foveal center. Because our method has π-ambiguity, it limits measurements to values between 0° and 180°. Thus in the figure, phase wrapping occurs every 180°. Note that four phase wraps (720°) appear in the figure for a full 360° rotation about the fovea. This is because angles in the Poincaré sphere space are twice that in the real space (retina). Specifically, axis orientation on the QU-plane of the Poincaré sphere varies from 0°, + 45°, 90°, −45°, and finally back to 0°, for a total of 360° on the sphere, but this corresponds to only a 180° rotation on the fovea [21]. Taking this factor of two difference into account, our results are consistent with that reported by Pircher et al [26].

The figure also shows that the fast axis orientation is largely insensitive to radial position. Axis orientation is preserved along lines radiating outward from the fovea and consistent with the known radial pattern of Henle fibers and that observed by others [22, 26]. Figure 6(B) shows axis traces for specific retinal eccentricities. At 2.1° eccentricity, minima and maxima approach 0° and 180° with the fast axis orientation following an almost linear decrease from one maximum to the next minimum, similar to what we expect of fibers that originate from the fovea and extend radially. At 6.8° eccentricity, the regular pattern of the fast axis is largely lost. Here the fibers are either less coherently organized, or the reduced phase retardation makes the fast axis measurement more unreliable.

7. Conclusion

We have demonstrated a new method based on PS-OCT for quantifying phase retardation and fast axis orientation of HFL in subjects. Measurements are consistent with earlier reports using confocal scanning laser polarimetry and Mueller matrix polarimetry, but with the added benefits of absolute DPPR measurements, axial separation of HFL birefringence, and no assumptions about the uniformity and linearity of the different sources of phase retardation in the eye. The average maximum DPPR at 840 nm for the three subjects is 22.0° (range: 20.4° to 23.0°) occurring at an average retinal eccentricity of 1.8° (range: 1.5° to 2.25°). Outside the ring, a floor of approximately 6.8° was measured, which we show can mainly be attributed to phase noise that is induced in the polarization states. Measurement of fast axis orientation is consistent with the known radial pattern of Henle fibers.