Modeling hematopoietic system response caused by chronic exposure to ionizing radiation

Abstract

A new model of the hematopoietic system response in humans chronically exposed to ionizing radiation describes the dynamics of the hematopoietic stem cell compartment as well as the dynamics of each of the four blood cell types (lymphocytes, neutrophiles, erythrocytes, and platelets). The required model parameters were estimated based on available results of human and experimental animal studies. They include the steady-state number of hematopoietic stem cells and peripheral blood cell lines in an unexposed organism, amplification parameters for each blood line, parameters describing proliferation and apoptosis, parameters of feedback functions regulating the steady-state numbers, and characteristics of radiosensitivity related to cell death and non-lethal cell damage. The model predictions were tested using data on hematological measurements (e.g., blood counts) performed in 1950–1956 in the Techa River residents chronically exposed to ionizing radiation since 1949. The suggested model of hematopoiesis is capable of describing experimental findings in the Techa River Cohort, including: i) slopes of the dose-effect curves reflecting the inhibition of hematopoiesis due to chronic ionizing radiation, ii) delay in effect of chronic exposure and accumulated character of the effect, and iii) dose-rate patterns for different cytopenic states (e.g., leukopenia, thrombocytopenia).

Introduction

Although exposure to ionizing radiation (IR) is a well-established risk factor for various disorders of the hematopoietic system (e.g., short-term effects like cytopenia, and long-term effects like leukemia), many quantitative aspects of the dynamics of the hematopoiesis response to IR during many years of chronic exposure still require additional investigation. Despite substantial efforts in studying regularities of functioning of the hematopoietic system, neither mechanisms forming the response patterns to IR nor factors contributing to individual variability are currently known. Partly this is because the experimental information on the effects of chronic radiation from animal and human studies is limited. Current progress in studies of deterministic effects of chronic exposure to IR on the hematopoietic system was recently summarized by Fliedner and Graessle (2008), who reviewed eleven accidents involving exposure of humans.

Recently Akleyev et al. (2010) presented new results on the hematopoiesis inhibition. In that paper we identified and quantitatively described the association between some characteristics of chronic (low dose-rate) exposure to (low-LET) IR and cellularity of peripheral blood cell lines. About 3,200 hemograms (i.e., spectra of blood counts) obtained during the years of maximal exposure to IR (1950–1956) for inhabitants of the Techa River were used in these analyses. The study group was comprised of exposed individuals who had been followed up by researchers from the Ural Research Center for Radiation Medicine from 1950 to 1956 (the period of maximal IR exposure), and whose doses to the red bone marrow (RBM) had been estimated. The wide range of doses involved allowed analysis of the nature of the dose–response relationship based on internal comparisons (Kossenko et al. 2005). The results of these analyses demonstrated hematopoiesis inhibition that manifested by a decrease in peripheral blood cellularity and an increase in the frequency of cytopenia in all blood cell lines (leukocytes including lymphocytes, monocytes, neutrophiles, as well as platelets and erythrocytes).

The data analysis applied in Akleyev et al. (2010) was based on traditional empirical and regression methods, and the model presented to explain the obtained results was statistically based. However, it may also be interesting to investigate how the results obtained can be interpreted in terms of some biologically-motivated model of hematopoiesis for individuals chronically exposed to low and intermediate doses of IR. One conclusion from the study of Akleyev et al. (2010) was that the contribution of specific confounding factors reflecting individual variability in response patterns was quantified and shown to be much less important than dose characteristics. This is in accordance with the well-known property of IR-induced effects that the primary inhibition response to IR (at least for high-dose acute exposure to IR) is largely a deterministic process (ICRP, 1991), i.e., that the process is predetermined by radiation dose and, to a much lesser extent, by individual heterogeneity. This allows development of a substantive model constructed on the basis of deterministic principles, and consideration of possible stochastic effects responsible for individual heterogeneity as corrections to the basic effect.

Another conclusion of the study was that the intensity of hematopoiesis inhibition in the period of maximal exposures is determined by the combined influence of dose rate and cumulative dose. The best predictor among dose characteristics was identified for each blood cell line to be the dose rate in (or one/two years before) the year of measurement and was largely related to the cumulative character of the effect. The notion of the best predictor was implemented partly because of the statistical collinearity between dose rate and cumulative dose: a high correlation between these two parameters prevented reliable discrimination between their contributions. This problem can be solved within the substantive model of data in which both effects are modeled based on substantive assumptions resulting in distinct functional forms of their contributions. To investigate separate contributions of both dose parameters is one of the goals of this paper.

Recent advances in mathematical modeling of hematopoiesis is reviewed in Adimy et al., (2006a,b), Fliedner and Graessle (2008), and Foley and Mackey (2009). Specific models focused on different research areas including i) mechanisms of proliferation and self-maintenance of hematopoietic stem cells (HSC), ii) mechanisms responsible for production of specific hematopoietic cell lines such as leukocytes, erythrocytes, and platelets, and iii) dynamics of peripheral blood characteristics at normal and pathological states of an organism (e.g., dynamics of the response of the hematopoietic system to acute and chronic exposure to IR).

Mathematical models of the dynamics of specific hematopoietic lines under chronic exposure to IR were suggested by Hofer et al. (1995), Tibken and Hofer (1995), Graessle (2000), Smirnova (2000, 2007), and Graessle and Fliedner (2010). The mathematical and computer model of hematopoiesis response to chronic exposure to IR developed in the present paper combines findings, ideas, and approaches from a majority of these studies. The present model is based on the model of hematopoiesis developed by Mackey and colleagues (see Colijn and Mackey (2005), Foley and Mackey (2009), and references therein). The model takes into account the dynamics of the HSC compartment as well as each of the three blood cell types (red blood cells, white cells, and platelets). The dynamics of all compartments are linked in this model. This remarkable property of the model allows for simultaneous analysis of the effects in different blood lines; therefore, this property was determinative in selecting the basic approach for further generalization and applying it on the results of Akleyev et al. (2010). The model is elaborated in detail especially with respect to i) evaluating model parameters by using available data, ii) uncovering many useful properties of the model by methods of nonlinear dynamics, and iii) explaining and quantitatively describing the cyclic phenomena in hematopoiesis, such as cyclical neutropenia and chronic myelogenous leukemia. The model, however, requires further generalization to take into account the effects of chronic exposure to IR. The model compartments are those which are potentially subject to damages after exposure to IR and whose response to chronic exposure to IR is typically measured (Akleyev et al. 2010). Therefore, a model being generalized for incorporating the effects of IR is appropriate for describing the data and modeling deterministic effects of chronic exposure to IR. Two types of the IR-induced effects need to be incorporated into the generalized model: i) dose rate effects implemented as in models of Smirnova (2000, 2007) and ii) effects of cumulative doses motivated by approaches of Graessle (2000). Furthermore, the compartment that represented leukocytes in Colijn and Mackey (2005) needs to be divided into sub-compartments describing lymphocytes and granulocytes. This is because of the different radiosensitivity of these lines which requires different approaches for their modeling.

Materials and methods

Models of deterministic effects of chronic radiation exposure in hematopoiesis

The generalized model used here includes compartments corresponding to HSC (S) and mature neutrophiles (N), lymphocytes (L), erythrocytes (R), and platelets (P) (Fig. 1). The respective system of delay differential equations is (Eqs. 1)

$$\frac{dS(t)}{dt}=-(\mathrm{\beta }(t)-\mathrm{\beta ̅}(t)+k_N(t)+k_R(t)+k_P(t)+k_L(t))S(t)+2e^{-({\gamma }_S+{\epsilon }_0){\tau }_S}(\mathrm{\beta }(t_S)-\mathrm{\beta ̅}(t_S))S(t_S)-\mathrm{\epsilon ̅}S(t_d)\frac{dN(t)}{dt}=-({\mathrm{\gamma }}_N+{\mathrm{\epsilon }}_N)N(t)+A_N{e}^{-{\tau }_N{\epsilon }_0}{k}_N(t_N)S(t_N),\frac{dL(t)}{dt}=-({\mathrm{\gamma }}_L+{\mathrm{\epsilon }}_L)L(t)+A_L{e}^{-{\tau }_L{\epsilon }_0}{k}_L(t_L)S(t_L),\frac{dR(t)}{dt}=-({\mathrm{\gamma }}_R+{\mathrm{\epsilon }}_R)R(t)+A_R(e^{-{\tau }_R{\epsilon }_0}{k}_R(t_R)S(t_R)-e^{-{\tau }_{RS}({\gamma }_R+{\epsilon }_R)}{k}_R(t_{R+RS})S(t_{R+RS})),\frac{dP(t)}{dt}=-({\mathrm{\gamma }}_P+{\mathrm{\epsilon }}_P)P(t)+A_P(e^{-{\tau }_P{\epsilon }_0}{k}_P(t_P)S(t_P)-e^{-{\tau }_{PS}({\gamma }_P+{\epsilon }_P)}{k}_P(t_{P+PS})S(t_{P+PS})).$$ (1)

with initial values S_*0, N_*0, L_*0, R_*0, and P_*0 corresponding to the steady-state of an unexposed organism, β is the proliferation rate of HSC, A_Q and k_Q (Q ∈ {N, L, P,R}) denote amplification factors and rates of differentiation into respective blood lines, t with subscripts define time delays (t_S = t + τ_S, etc.), and terms with β̅, and all kinds of ε in Fig. 1 and Eqs. (1) show the effects of chronic exposure to IR.

Fig 1.

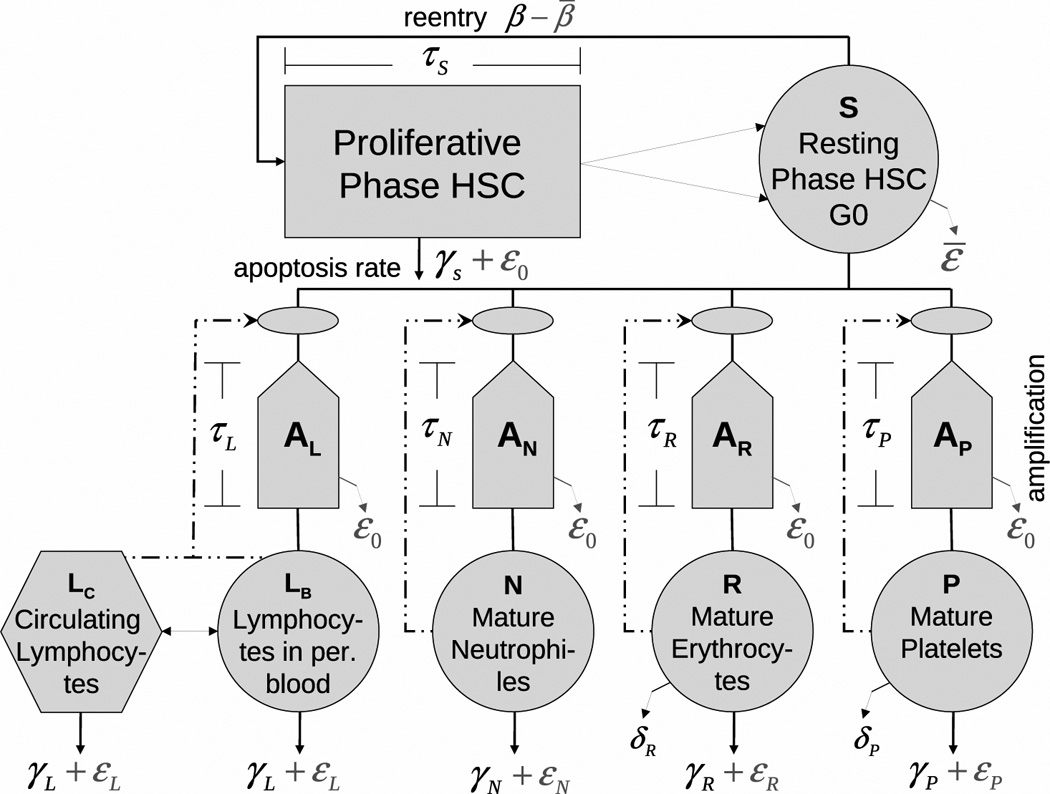
Model of hematopoiesis under chronic exposure to IR. The circles describe five model compartments corresponding to HSC (S) and mature lymphocytes (L), neutrophiles (N), erythrocytes (R), and platelets (P). The pentagons denote compartments for amplification and maturation of blood cells. The rectangle shows the compartment of HSC proliferation. The hexagon shows the compartment of circulating lymphocytes. Solid lines show cell transitions between compartments, while dash-dotted lines show feedback loops regulating the peripheral blood counts. The solid lines with arrows represent different modes of cell death: i)γ’s correspond to natural apoptosis, ii)ε’s correspond to radiation-induced apoptosis, and iii)δ’s correspond to senescence death of platelets and erythrocytes.

The compartment “S” contains pluripotential and self-renewing HSC that can proliferate and differentiate in one of the four lines of peripheral blood: lymphocytes, neutrophiles, erythrocytes, or platelets. In this compartment, the dynamics of HSC is described by the first equation in Eqs. (1). Inflow to this compartment is formed by proliferation in this compartment regulated by a feedback loop. During time of proliferation (τ_S) HSC are subject to apoptosis. The four other equations in Eqs. (1) represent respective models for peripheral blood lines. These models share some common features and display some differences. All models of peripheral blood lines contain a feedback loop regulating the inflow from the HSC compartment. Incoming cells are subject to amplification such that one HSC produces A_Q cells forming the inflow to the Q^th peripheral compartment (Q ∈ {N, L, P, R}). Cells of peripheral blood are subject to random death through apoptosis. In addition, all survived platelets and erythrocytes are subject to senescence death.

Presumptive mechanisms of negative feedback mediated by lymphokines, thrombopoietin, erythropoietin, and the granulocyte colony stimulating factor as well as a local regulatory loop within the pluripotent HSC population, are modeled by Hill-type functions:

$$\beta (t)={\mathrm{k̅}}_s\frac{{\theta }_S^{d_S}}{{\theta }_S^{d_S}+S{(t)}^{d_S}}\text{and}{k}_Q(t)={\mathrm{k̅}}_Q\frac{{\theta }_Q^{d_Q}}{{\theta }_Q^{d_Q}+Q{(t)}^{d_Q}}$$ (2)

for compartments of HSC and peripheral blood (Q ∈ {N, L, P, R}), respectively; k̅_s, d_S, θ_S, k̅_Q, d_Q, and θ_Q are model parameter to be estimated.

All model features briefly mentioned above were implemented in the original model of Colijn and Mackey (2005). Two important generalizations critical to the present study deal with implementation of lymphocyte lineage and incorporating the effects of chronic exposure to IR. Generally speaking lymphocyte lineage can be modeled in the same way as other blood lines: they originate in red bone marrow and are subject to amplification and maturation. Inflow from the HSC compartment is also regulated by a negative feedback loop. Certain specifics such as negative/positive selection in thymus can be mimicked by assigning these processes to the HSC compartment and/or amplification compartment. Note that we consider the hematopoietic system with a mean antigene load. One justification for this is that the health state defined by acute and chronic conditions (characterized by available ICD-9-CM codes) was taken into account in the analyses of the Techa River data presented by Akleyev et al. (2010). Note also that we compare results of these analyses with predictions of the current model; therefore, the approximation of a mean antigen load is justified. However, there are critical features in lymphocytopoiesis which cannot be avoided and must be explicitly presented in the model. This includes the part of lymphocytes circulating in the other functional organs, such as limp nodes, lung, spleen, etc. In contrast to other blood lines, only a small part of all lymphocytes are in peripheral blood (about 2%) and therefore only this part is measured in blood tests. A quantitative picture of lymphocyte development is presented in Hofer et al. (1995) and Wuestermann and Cronkite (1995).

In the generalized model, cells in all compartments are subject to chronic exposure to IR. There are three types of IR-induced cell effects included in the generalized model. The first is cell damages resulting in cell death (interphase (hours) or mitotic (days)) and non-lethal cell damages resulting in an augmentation of the compartment of injured cells. The second is the suppression of HSC proliferation (−β̅), which is proportional to the number of injured cells. The third is the excess cell loss resulting from increased apoptosis in HSC, peripheral blood as well as during amplification and maturation. The first-type effects are proportional to dose rate, while the effects of other two types are proportional to cumulative radiation dose; therefore we speak about the effect of dose rate and the effect of cumulative dose.

Mathematically, Eqs. (1) represent a system of delayed differential equations. Six time delays are used in the model: i) the HSC proliferation time τ_s, ii-v) the maturation time of neutrophiles (τ_N), lymphocytes (τ_L), erythrocytes (τ_R), and platelets (τ_P), and vi) delayed cell death (τ_d) induced by IR. The Matlab solver dde23 was used to solve Eqs. (1). The properties of this solver are described and discussed by Shampine and Thompson (2001) and Bellen and Zennaro (2003).

Strategy of model estimation

A feature of the model is that almost all its parameters have a clear biological meaning and can be estimated from available data. Since it was intended to incorporate the experimental results presented in Akleyev et al., (2010), the strategy for estimation of non-IR terms adopted here slightly differs from that used in the original paper of Colijn and Mackey (2005). First, by using measurements of steady-state blood counts in peripheral blood (Akleyev et al., 2010) and standard values for the renewal rate, i.e., daily cell flux to peripheral blood (Fliedner et al., 2002, Fliedner and Graessle, 2008), the rates of apoptosis of cells in peripheral blood were estimated. For example, the neutrophile apoptosis rate was calculated as γ_N = R_N / N_*0, where R_N is the granulocyte renewal rate. Second, parameters for the hematopoietic feedback loop (except θ_S and k̅_Q, Q ∈ {N, L, P,R}), amplification factors, and time delays were taken from Colijn and Mackey (2005). Parameters for lymphopoiesis were taken similarly to those of granulocyte lineage, i.e., A_L = A_N, τ_L = τ_N, d_L = d_N = 1, and θ_L / L_*0 = θ_N / N_*0. Third, the steady-state value S_*0 was estimated using an algebraic equation for steady-state of HSC compartment (Eq. 3)

$$\frac{R_N}{A_N}+\frac{R_L}{A_L}+\frac{R_P}{A_P(1-E_P)}+\frac{R_R}{A_R(1-E_R)}=f_S{k}_{S*}{S}_{*0}$$ (3)

where k_S* = 0.06 d⁻¹, E_Q = exp(−γ_Qτ_QS) for Q ∈ {P, R}), and f_s = 2 exp(−γ_Sτ_S) −1.

Fourth, θ_S was estimated as solution of Eq.(2) taken for the steady state, i.e., ${\mathrm{k̅}}_s{(1+(S_{*0}/{\theta }_S^{d_S}))}^{-1}=k_{S*}=0.06$. Finally, estimation of parameters k̅_L, k̅_N, k̅_R, and k̅_P using algebraic equations for steady-states in respective blood cell lines (e.g., κ_*N = R_N /(A_NS_*0)) completes the estimation of the non-IR part of the model. Numerical estimates of all these parameters are given in Table 1.

Table 1.

Parameter estimates for non-IR terms: d denotes days; [S] is given in 10⁶ cells/kg, while [L], [N], [R], and [P] are given in 10⁹ cells/kg

	Renewal rate	Steady State		Apoptosis rate	Parameters of Hill functions			Amplification number	Proliferation/m aturation and aging times
Q	RQ [Q]/ d	Q*0 [Q]/ kg	κQ* %d−1	γQ d−1	κ̅Q d−1	θQ [Q]/ kg	dQ	AQ	τQ (d)	τQM (d)
S	3.32	1.55	6.0	0.1	3.0	0.58	4		2.8
N	120	0.33	1.47	5.3	0.15	0.036	1	75200	3.5
L	20	9.81	0.25	0.029	0.027	0.98	1	75200	3.5
R	200	368.	0.56	0.0078	1.88	160	6.96	563000	6.0	111.2
P	150	20.6	0.78	0.10	0.24	1.49	1.29	282000	7.0	9.5

Dose rate (r_d) effects, e.g., IR-induced cell death for HSC and peripheral blood per unit of time, are defined by the dose rate at the moment of t and are represented as r_d / D₀, where D₀ is a known characteristics of radiosensitivity of HSC and peripheral lymphocytes. Values of D₀ are taken according to Fliedner et al. (2002): D_0S = 0.6 Gy, D_0L = 1.4 Gy, D_0N = D_0P = D_0R = 50 Gy. Effects of cumulative dose (C_d) include the rate of cell injuring resulting in increased apoptosis of peripheral blood cells and suppression of proliferation rate in the HSC compartment. These effects are represented as αC_d, where the parameter α is preliminarily estimated by a data fit (manual search) or evaluated using arguments in Graessle (2000) and Fliedner and Graessle (2008). Specifically, models describing suppression of HSC proliferation, −β̅ (t) = −α₁C_dβ (t), and describing excess cell loss, ${\epsilon }_0=r_d{D}_0^{-1}+{\alpha }_2{C}_d{\gamma }_s,\mathrm{\epsilon ̅}=r_d{D}_0^{-1},{\epsilon }_Q=r_d{D}_{0Q}^{-1}+{\alpha }_2{C}_d{\gamma }_Q$ for Q ∈ {N, L, P, R}, were used in the present numerical analyses. The corresponding parameters were estimated as α₁ = 0.1Gy⁻¹ and α₂ = 0.2Gy⁻¹.

Steady State and analytical properties of the model

Two types of steady-state solutions of the Eqs. (1) can be investigated. The first corresponds to the case of an unexposed population (i.e., when r_d = 0 and C_d = 0). The corresponding values S_*0, N_*0, L_*0, R_*0, and P_*0 are interpreted as means of respective blood counts of an unexposed organism, and serve as the initial values for the Eqs. (1) for chronic IR exposure. The second steady state corresponds to an exposed organism denoted as S_*, N_*, etc. This steady state is achieved for a fixed dose rate and fixed cumulative dose effects (see example in the end of this subsection). Both steady states are related, and the model permits an analytical solution of the main linear contributions (denoted as S̃, Ñ, L̃, R̃, and P̃) to the decline in blood counts in a new steady-state, i.e., the linear contributions that are proportional to dose rate and cumulative dose as Q_* = Q_*0 (1+Q̃_dr_d + Q̃_CC_d + o(r_d, C_d)), Q ∈ {S, N, L, P, R}. The strategy of calculations of these linear contributions is straightforward. First, the system of algebraic equations providing the steady state solution is constructed from Eqs. (1). Then, the right-hand sides of all equations are expanded in time series keeping only terms not higher than linear in dose rate (r_d) and cumulative dose (C_d). Using the algebraic equations describing the unexposed steady states, one can obtain the result in the following form (Eqs. 4–7). For the HSC compartment they read

$${\mathrm{S̃}}_d=\frac{-1}{Z}(\frac{1+{\kappa }_{S*}(1+f_S){\tau }_S}{D_0}+\sum _Q{\mathrm{d̅}}_Q{\kappa }_{Q*}(\frac{1}{{\gamma }_Q{D}_Q}+\frac{{\tau }_Q}{D_0})+\sum _{Q\text{'}}{\mathrm{d̅}}_{Q\text{'}}{\kappa }_{Q\text{'}*}{E}_{Q\text{'}}(\frac{{\tau }_{Q\text{'}S}}{D_{Q\text{'}}}-\frac{{\tau }_{Q\text{'}}}{D_0}\left)\right){\mathrm{S̃}}_C=-\frac{{\alpha }_1{\kappa }_{S*}{f}_S}{Z}-\frac{{\alpha }_2}{Z}({\kappa }_{S*}(1+f_S){\tau }_S{\gamma }_S+\sum _Q{\mathrm{d̅}}_Q{\kappa }_{Q*}(1+{\tau }_Q{\gamma }_S)+\sum _{Q\text{'}}{\mathrm{d̅}}_{Q\text{'}}{\kappa }_{Q\text{'}*}{E}_Q({\tau }_{Q\text{'}S}{\gamma }_{Q\text{'}}-{\tau }_{Q\text{'}}{\gamma }_S))$$ (4)

where Q ∈ {N, L, P,R}, Q' ∈ {P,R}, and Z = κ_S*f_SF_Sd_S − ∑_Qd̅_Qκ_Q*.

For peripheral blood they are

$${\mathrm{Q̃}}_d=\frac{1}{1+d_Q{F}_Q}({\mathrm{S̃}}_d-\frac{1}{{\gamma }_Q{D}_Q}-\frac{{\tau }_Q}{D_0}){\mathrm{Q̃}}_C=\frac{1}{1+d_Q{F}_Q}({\mathrm{S̃}}_C-{\alpha }_2(1+{\gamma }_S{\tau }_Q))$$ (5)

for neutrophiles and lymphocytes (i.e., Q ∈ {N, L}), and

$${\mathrm{Q̃}}_d=\frac{1}{1+d_Q{F}_Q}({\mathrm{S̃}}_d-\frac{1}{{\gamma }_Q{D}_Q}-\frac{{\tau }_Q}{D_0}-\frac{E_Q}{1-E_Q}(\frac{{\tau }_Q}{D_0}-\frac{{\tau }_{QS}}{D_Q}\left)\right){\mathrm{Q̃}}_C=\frac{1}{1+d_Q{F}_Q}({\mathrm{S̃}}_C-{\alpha }_2(1+{\gamma }_S{\tau }_Q+\frac{E_Q}{1-E_Q}({\gamma }_S{\tau }_Q-{\gamma }_Q{\tau }_{QS})\left)\right)$$ (6)

for erythrocytes and platelets (i.e., Q ∈ {R, P}).

Notation used in these formulae are defined in Eq. (3) and by

$$F_Q=\frac{Q_{*0}^{d_Q}}{{\theta }_Q^{d_Q}+Q_{*0}^{d_Q}},{\mathrm{d̅}}_Q=\frac{d_Q{F}_Q}{d_Q{F}_Q+1}.$$ (7)

Figure 2 presents the typical time dynamics provided by the model. It illustrates the compatibility of the model based on the delay differential equations (Eqs. 1) and its approximation based on Eqs. (4–7). For Fig. 2, the following exposure pattern is used. A five-year dynamics is considered.

Fig 2.

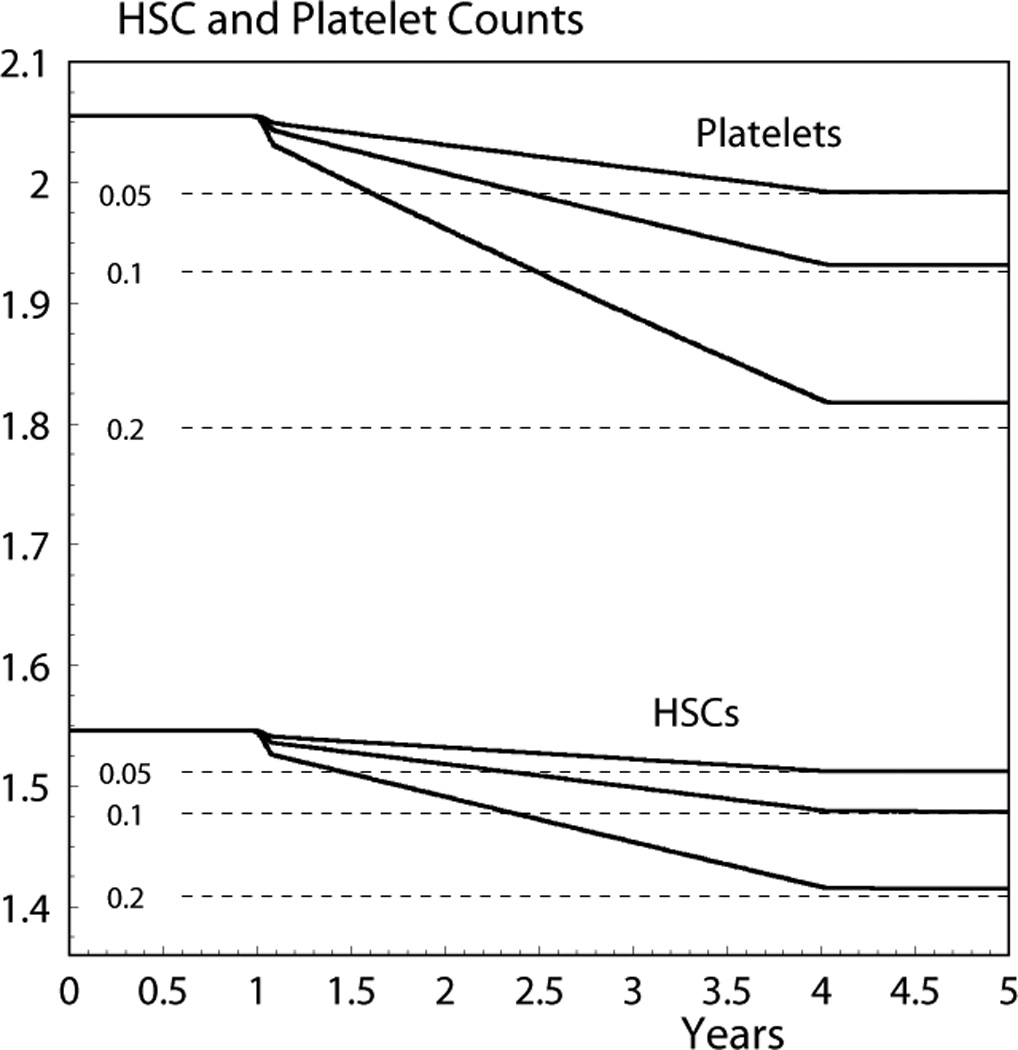
Five-year dynamics of HSC (in 10⁶ cells/kg) and platelet (in 10¹⁰ cells/kg) counts given by Eq. (1); the dashed line shows the final steady state given by the approximate model (Eqs. 4 and 6). The numbers at the left of the dashed lines denote dose rate in Gy/year for which the dynamics were calculated.

There is no exposure during the first year and the dose rate, r_d, is constant from the second to the fifth year. Three cases are considered: r_d =0.05 Gy/year, r_d =0.1 Gy/year, and r_d =0.2 Gy/year. The cumulative dose effect modeled at a time t is contributed by IR exposure during the most recent three-year period prior to the time t. Therefore, the system is in the initial steady state during the first year and in the final steady state during the fifth year. Figure 2 shows only HSC and platelets, but the shapes of all other compartments are qualitatively the same. The quantitative characteristics of the dynamics of all compartments are presented in Table 2. Analysis of the differences between the steady states after IR exposure (estimated using the approximation or the exact numerical solution of Eqs. 1) and the initial steady states presented in column Q_*0 of Table 1 allows us to conclude that the approximation captures more than 90% of the dose effect, and that its quality is better for lower dose rates. Note that short-term oscillations predicted by the model are not essential here and, therefore, were smoothed using the Matlab “Filter” function. Note also that the dynamic patterns shown in Fig. 2 are typical for chronic exposure experiments, e.g., they qualitatively coincide with patterns presented in Fig. 5 in Fliedner and Graessle (2008).

Table 2.

Steady states of blood counts at the end of exposure in 10⁶ cells/kg for HSC and in 10⁹ cells/kg for other blood lines

	rd =0.05 Gy/year		rd =0.1 Gy/year		rd =0.2 Gy/year
	Exact	Approx.	Exact	Approx.	Exact	Approx.
HSC	1.5123	1.5119	1.4791	1.4775	1.4150	1.4088
Neutrophiles	0.3159	0.3157	0.3057	0.3048	0.2866	0.2829
Lymphocytes	9.4927	9.4845	9.1866	9.1548	8.6156	8.4953
Erythrocytes	364.83	364.78	361.83	361.68	356.00	355.48
Platelets	19.922	19.909	19.316	19.263	18.175	17.971

Fig 5.

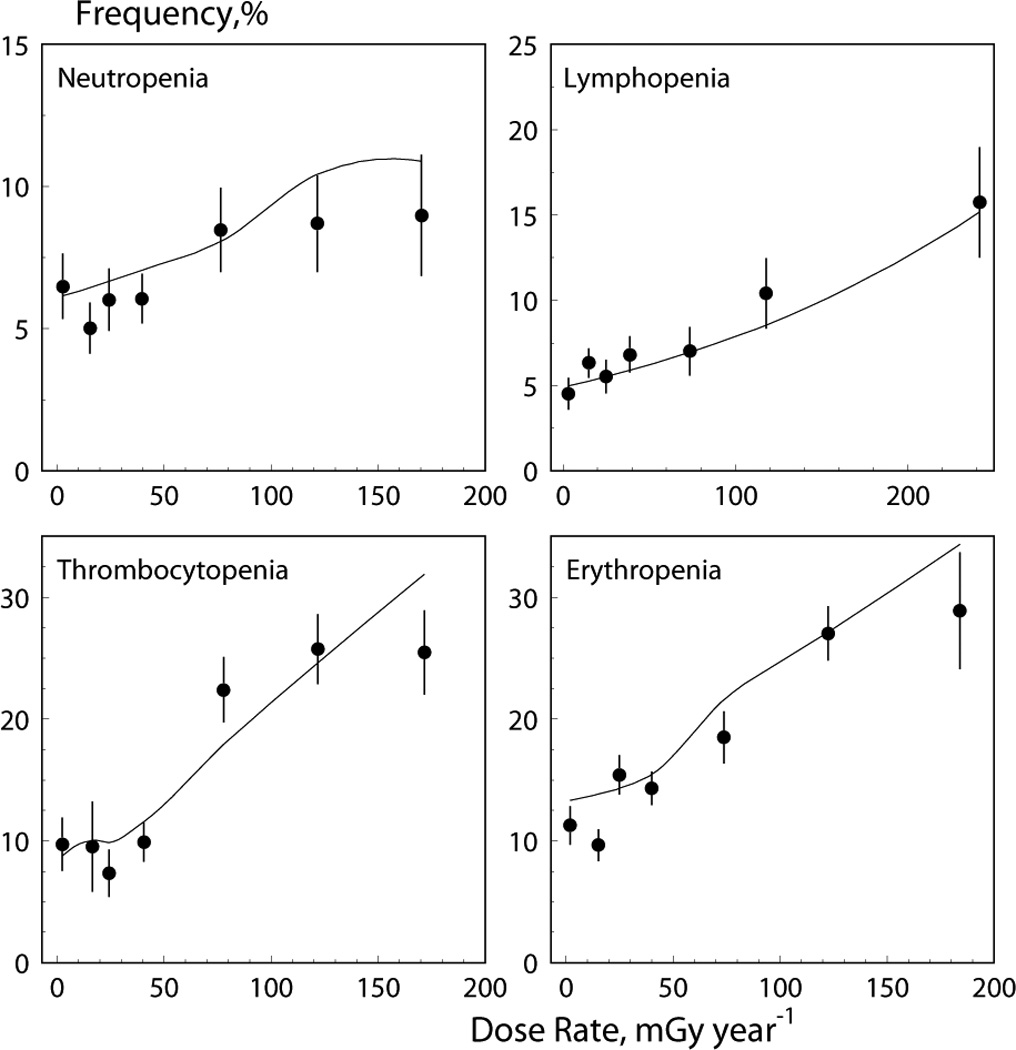
Data on cytopenia frequency (dots) and model prediction (solid lines) for four blood lines.

Experimental Results and Model Prediction

Experimental results which have to be described by the model can be summarized as follows (Akleyev et al. 2010): First, the relative dose-rate decline β / u (given in units of year · Gy⁻¹, and estimated by generalized linear models, i.e., C = u + βr_d = u (1+β / u)r_d), where C and r_d are the measured blood cell counts and dose rate) is −0.82 for lymphocytes, −0.74 for neutrophiles, −0.33 for erythrocytes, and −1.06 for platelets, respectively. Second, the dose rate at the moment of measurement is not the best predictor of the blood count decline, i.e., the effect of exposure history is important. Third, the frequency of cytopenic states increases with dose rate (or with another dose parameter identified as the “best predictor”), and this increase is approximately linear.

The developed model is capable of describing these findings. The measured relative declines in blood cell counts caused by the dose rate are related as 2.2 : 2.5 : 1.0 : 3.2 for neutrophiles, lymphocytes, erythrocytes, and platelets, respectively. These ratios can be calculated analytically by Eqs.(1): 2.9 : 5.3 : 1.0 : 3.6. Thus, the relative decline is in approximate agreement with the model predictions if the dose rate effect dominates or if the cumulative dose effect is proportional to the dose rate effect. Interestingly, a simple analytical result for these ratios can be obtained by making several additional approximations to Eqs. (4–7). Since S̃_d dominates in the dose rate effect in peripheral blood lines and F_Q ≈ 1, the ratios can be approximated by

$$\frac{d_R+1}{d_N+1}:\frac{d_R+1}{d_L+1}:1:\frac{d_R+1}{d_P+1},$$ (8)

which is 3.9 : 3.9 : 1.0 : 3.5. This result shows that speed of feedback between blood counts and the HSC compartment is determinative in the effect of dose rate.

A numerical analysis shows that the pure dose-rate effect (i.e., terms containing Q̃_d) explains only 10% for lymphocytes and about 5% for the other blood lines of the total decline observed in the data (Q̃_d,L / 0.82 = 0.093, Q̃_d,N / 0.74 = 0.055, Q̃_d,P / 1.06 = 0.048, and Q̃_d,R / 0.33 = 0.043). All parameters describing the dose-rate effect are taken from other experiments, so there is no room for fitting. It is concluded that calculation of the absolute decline requires careful modeling of the pool of injured cells. In the previous subsection it was assumed that the number of injured cells is proportional to the cumulative dose in Gy (C_d), such that β̅ = 0.1C_dβ (corresponding to experimental results in vitro) and the excess cell losses increased by 0 2C_dγ_R. A more realistic approach can be constructed assuming that the contributions of dose rates in prior years which form the total cumulative dose, depend on the time before measurements. This can be achieved by the following substitution

$${\alpha }_2{C}_d\to \alpha \underset{0}{\overset{t_{\text{exp}}}{\int }}{f}_W(u,\{{\theta }_W\})r_d(u)du$$ (9)

and similar for α₁, where f_W (u, {θ_W}) is a density, representing a mixing distribution including a set of parameters {θ_W}, which describe the dose rate contributions measured in prior years, and t_exp is the total exposure time period.

Results of Akleyev et al. (2010) show that the dose-rate effect can be delayed; so this distribution has to be quite flexible to capture such an effect. Uniform, exponential, and Weibull distributions were tested to describe the mixing distribution for each blood line.

The likelihood function of data can be written as ∏_if_b (μ_d,ξ), where f_b (μ_d,ξ) is the distribution of blood counts. The following models for f_b (μ_d,ξ) are considered: normal, gamma, log-normal, and inverse Gaussian. This set of distributions represents the extended set of models used in Akleyev et al. (2010). The mean of these distributions is denoted as μ_d and includes dose-rate and cumulative dose effects. Since doses are presented in the form of a piecewise linear function with nodes in the beginning (or in the end) of each year, the integral in Eq. (9) can be calculated and μ_d is expressed as,

$${\mu }_d={\mu }_0(1+r_{d0}{\mathrm{Q̃}}_d+\alpha {\sum }_{i=0}{r}_{di}(F(t_{i+1})-F(t_i)))$$ (10)

where F(t) is the distribution function of the mixing distribution from Eq. (9) (e.g., F(t) = 1 − exp (−(t/ λ_W)^k_w) for a Weibull and an exponential (k_W = 1) distribution, and F(t) = min(t / λ_W,1) for a uniform distribution); r_d0 is the dose rate measured in the year of the blood count measurements, r_di is the dose rate measured in the i^th year before the year of measurement, and t_i is the time between the time of measurement and the end of the i^th year (t₀ ≡ 0).

This form of the mean is used for all model distributions. Doses are incorporated into the model only through their occurrence in Eq. (10). Since all considered distributions are two-parametric, a spectrum of models can be defined depending on the choice of the second parameter which is dose-independent. For example, in the case of a gamma-distribution f(x) = (x / θ)^k_γ−1 exp(−xθ) /(Γk_γ)θ) (mean=θk_γ and variance= θ²k_γ), three models correspond to the following choice: i) θ = σ² / μ_d, k_γ = μ_d / θ, where σ is dose-independent, ii) θ = σ² / μ_d, where k_γ is dose-independent, and iii)k_γ = μ_d / θ,where θ is dose-independent. Altogether ten models for each blood count were considered (one for the normal distribution, and three for the other distributions).

Parameter estimates for the best models are presented in Table 3. The model based on the normal distribution for erythrocytes is significantly better than all other models. The Gamma-model including the dose-independent shape parameter k_γ, and the lognormal model including the fixed parameter $\mathrm{\sigma ̃}(f(x)={(\sqrt{2\pi }\mathrm{\sigma ̃}x)}^{-1}\text{exp}(-{(\text{log}(x/{\mu }_d)+{\mathrm{\sigma ̃}}^2/2)}^2/(2{\mathrm{\sigma ̃}}^2))$, with a mean of μ_d and variance of ${\mu }_d^2(\text{exp}{\mathrm{\sigma ̃}}^2-1))$ describe other blood lines. The former is the best model for platelets while the latter is the best for neutrophiles. In both cases the difference in likelihoods compared to alternative models is statistically significant. Both these models describe the lymphocyte distribution equally well. The latter is chosen because the likelihood is a little higher. Note that values exceeding the 99% percentile in all blood count distributions were not used in the fitting procedures to exclude any possible pathological impact.

Table 3.

Parameters of the model for delay effects (see Eqs. 9 and 10) estimated for four blood lines. Alternative models are shown for neutrophiles and erythrocytes

	Blood count distributions	Mixing distribution	μ0 [C]1	Scale2 [C]1	α y Gy−1	kW	λW3 (y)	Mean (y)	Std (y)
Lymphocytes	Lognormal	Exponential	2.26	0.35	−0.73	1	0.017	0.017	0.017
Neutrophiles	Lognormal	Exponential	3.74	0.36	−0.68	1	0.72	0.72	0.72
Platelets	Gamma	Weibull	245.6	15.1	−1.47	1.69	1.13	1.01	0.61
		Uniform	245.7	15.1	−1.46		2.00	1.00	0.58
Erythrocytes	Normal	Weibull	4.30	0.40	−0.42	2.14	1.09	0.96	0.47
		Uniform	4.30	0.40	−0.42		1.92	0.96	0.55

¹[L]=[N]=[P]= 10⁹cells/mL and [R]= 10¹²cells/mL

²Scale parameter is blood count distribution specific: σ for normal and gamma distributions and σ̃ for a lognormal distribution

³λ_W for different mixing distributions is defined by Eq. (10).

Parameters of mixing distributions better representing the delayed effect of dose rates as well as their means and standard deviations are shown in Table 3. The exponential distribution was selected for lymphocytes and neutrophiles while the Weibull and uniform distributions are equally applicable for erythrocytes and platelets. Figure 3 shows the distributions (multiplied by −σ) for all considered mixture distributions. The plots in the figure reflect the delayed effects for all lines (except for lymphocytes) with means between 0.5 and 1.5 years that correspond to the best predictor of dose rate in the previous year. This again confirms our prior results described in Akleyev et al. (2010).

Fig 3.

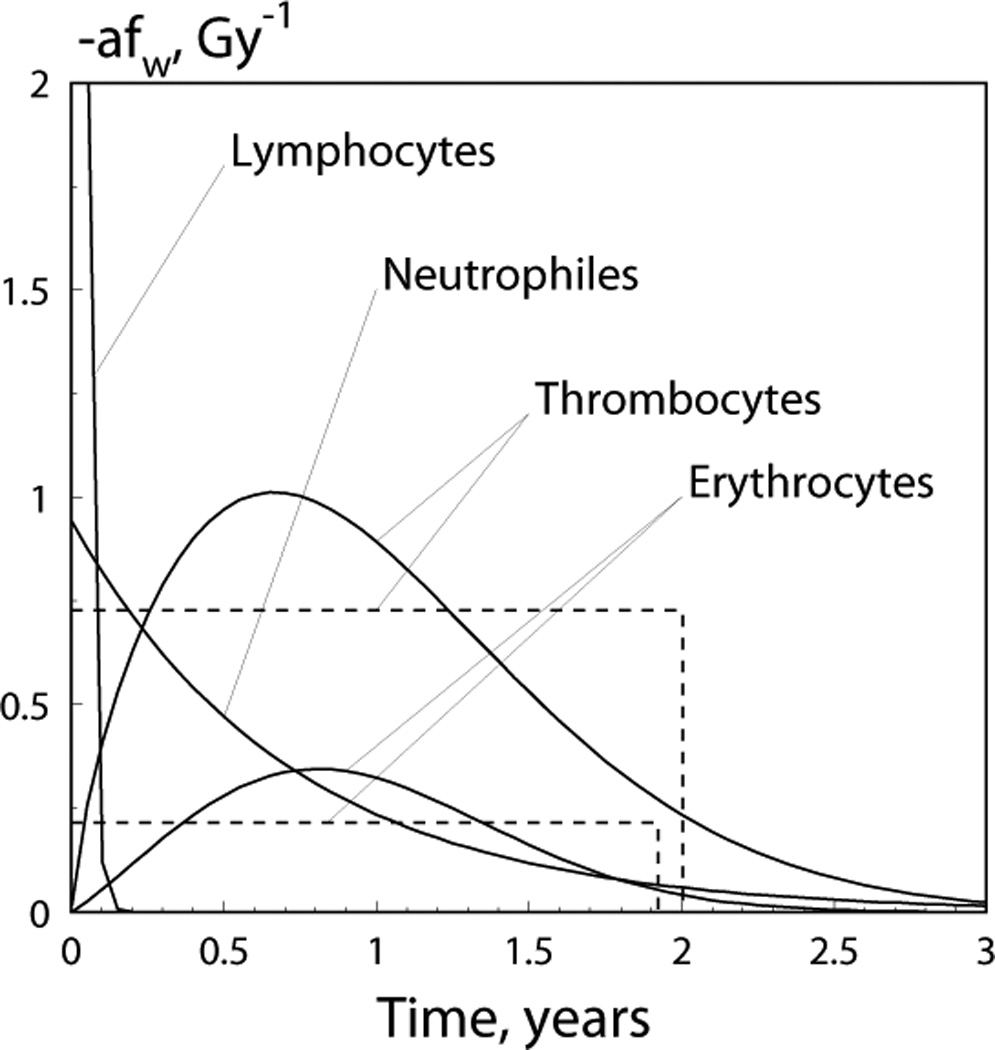
The distribution f_W (u, {θ_W}) (multiplied by −α) describes the delayed dose-rate effects for four blood lines (see Eq. (9) for definition of f_W (u, {θ_W}) and Table 3 for parameter estimates); the dashed lines show alternative distribution (i.e., uniform distribution) models for mixing distributions, for platelets and erythrocytes; the point where the graph intersects with the y-axis for lymphocytes is 42.01 Gy⁻¹.

The quality of data description by the model is illustrated in Fig. 4 in which means of blood counts calculated in six dose rate bins are compared to theoretical estimates of the mean as calculated using Eq. (10). Nonlinearity with dose rate in the theoretical predictions occurred because of different histories of chronic exposure (contributed by the last term in Eq. (10)) for different bins. The model is also capable of predicting the frequency of cytopenic states. Explicit expressions can be calculated by integration of the model distribution from zero to the norm, n, specific for each blood line: 2.0 for neutrophiles, 1.3 for lymphocytes, 180 (men) and 150 (women) for platelets, and 4,000 (men) and 3,700 (women) for erythrocytes (all in 10⁹ cells/L). These expressions can be given as $0.5[1+\mathrm{e}\mathrm{r}\mathrm{f}((n-{\mu }_d)/\sqrt{2}\sigma )]$ for erythrocytes (normal distribution), $0.5[1+\mathrm{e}\mathrm{r}\mathrm{f}((2\text{log}(n/{\mu }_d)+{\mathrm{\sigma ̃}}^2)/2\sqrt{2}\mathrm{\sigma ̃})]$ for lymphocytes and neutrophiles (lognormal distribution), and γ (k_γ, n / θ) / Γ (k_γ) (where γ (k_γ, n / θ) is the incomplete gamma function) for platelets (gamma distribution), respectively. Since the dose pattern is specific for each considered individual, the predicted probability was calculated for each individual. Figure 5 presents the modeled rate as the mean of the predicted individual probabilities and empirically estimated rate as in Akleyev et al. (2010), plotted for bins of the best predictors, i.e., for the dose rate of the year of measurements for lymphocytes, for the dose rate of the year prior of the year of measurements for erythrocytes, and for the mean of dose rates for three prior years, including the year of measurement, for neutrophiles and platelets, respectively.

Fig 4.

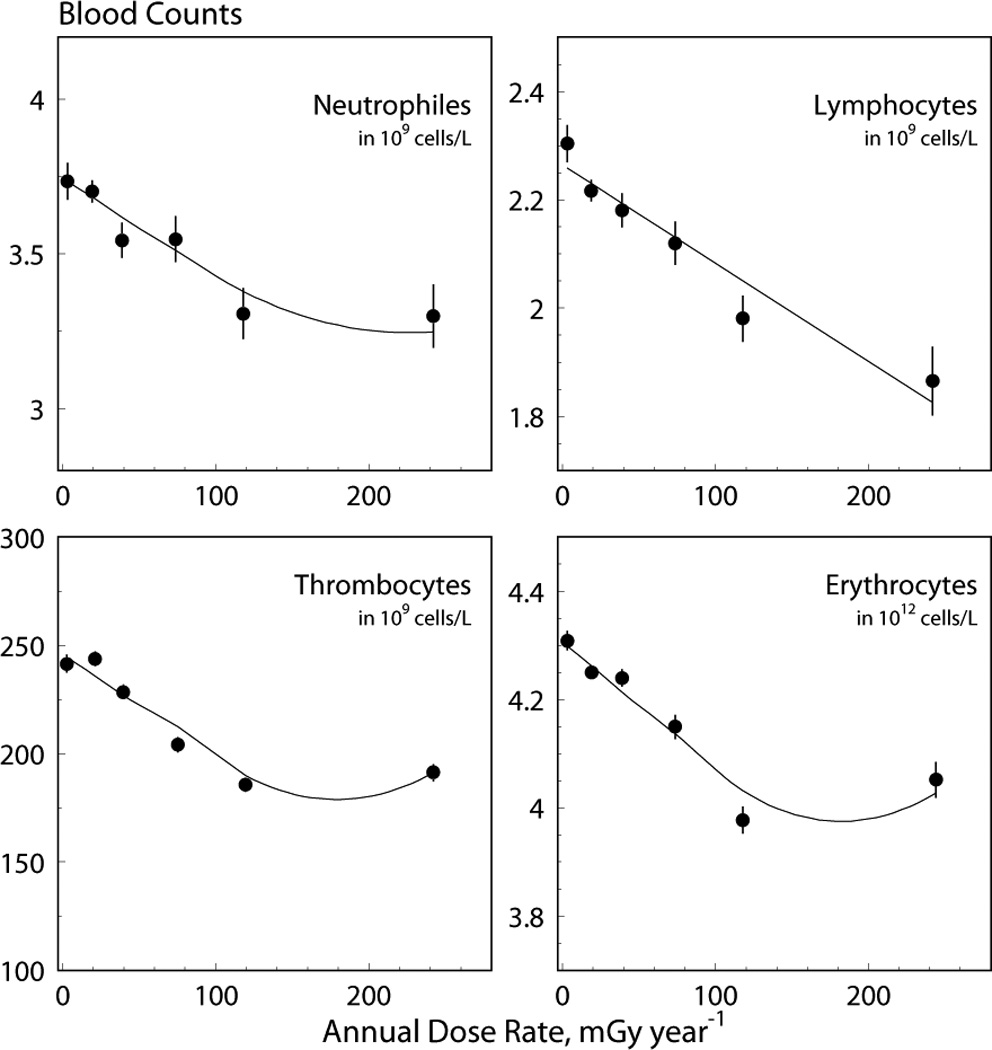
Data on blood counts (dots) and model prediction (solid lines) for four blood lines. The solid lines were obtained using a model with a Weibull distribution of the delayed dose-rate effect for platelets and erythrocytes and with an exponential distribution for neutrophiles and lymphocytes.

Discussion

Modeling approach

A new approach to comprehensive modeling of the hematopoietic system for humans exposed to IR is suggested in the present paper. The approach is based on the models of hematopoiesis developed by Mackey and colleagues (Colijn and Mackey 2005, Foley and Mackey 2009 and references therein) and generalizes them by inclusion of the effects of chronic IR exposure. The crucial property of the developed model is that it dynamically relates the HSC compartments to all lines of peripheral blood cells, when chronic exposure to IR is considered.

The style of modeling is a certain trade-off between a parsimonious approach (i.e., having a tendency to keep the minimal number of parameters) and a detailed description of each blood cell line using a multiple-compartmental structure. The first type approach was used by Dingli et al. (2007) and Dingli and Pacheco (2010), while the second type approach was used by Shochat et al. (2002).

In the area of modeling of hematopoiesis under acute or chronic exposure to IR, a detailed compartmental structure was developed by the group of Fliedner (see Fliedner and Graessle (2008) and references therein). This approach is based on a detailed description of the processes of differentiation and maturation of blood lines and allows for capturing many useful properties of hematopoiesis. However, it requires estimates of a large number of parameters, many of which are not currently known. Another example of a model that allows studying the effects of low-dose chronic and acute exposure to IR on hematopoiesis was developed by Smirnova (2000, 2007). The mathematical model of major hematological lines presented in these papers comprises both types of approaches mentioned above and, in this sense, this approach is closest to that used in the present paper. The model of Smirnova is presented by a system of differential equations in which the IR-induced cell damage is described in terms of the standard one-target-one-hit theory. This model can take into account specific features of thrombocytopoietic and granulocytic lines. A specific inhibitor of cell reproduction (chalone) is used to model the feedback mechanism regulating the HSC reproduction. The modeling approach takes into account only basic stages of the development of hematopoietic cells and the main regulatory mechanisms of its functioning. This model can be solved analytically in the case of constant transition rates between model compartments and a constant rate of chronic exposure to IR. The model allows for analytic solutions for steady-state, and therefore allows detailed analyses of radiation effects. Note, however, that the model described above has also some limitations, e.g., i) not all parameters can be identified from the available human data, ii) the chalone regulatory mechanism represents a general and approximate description of regulatory mechanism known in details now, and iii) all blood lines are modeled separately. Our approach was constructed to overcome the mentioned difficulties and appeared to be more appropriate for data we deal with.

All considered models use a compartmental structure. The critical property of compartment models is that statistical units (cells in this case) are homogeneous with respect to properties critical for the phenomenon of interest. In our case these properties are proliferation, apoptosis, amplification, and radiosensitivity, which are all represented by respective rates. It is realized however, that hematopoiesis and especially hematopoiesis under chronic IR exposure are quite complex phenomena to be represented by the limited set of pure homogeneous compartments. The two extreme cases discussed above (i.e., detailed or parsimonious approach for hematopoiesis modeling) result in models which are too complex or too simplified. In the first case the respective model requires too many parameters and too many assumptions, because the current state of experimental biology cannot provide the required detailed qualitative picture of hematopoiesis including the effect of possible heterogeneity among individuals. In the second case the respective models deal with heterogeneous compartments; the resulting estimates and predictions are too general, which makes biological interpretation difficult and not unambiguous.

The modeling approach illustrated in Fig. 1 and mathematically formalized by a system of delayed differential equations represents a reasonable compromise between these extreme modeling styles. In the present approach all blood lines are modeled maximally similar, although several important specific features are implemented. For example, the effects of cell death caused by senescence were implemented only for platelets and erythrocytes, or circulation effects were also taken into account for lymphocytes. However, there are compartments which were not included in the model, e.g., those compartments in RBM that represent specific stages of blood cells differentiation. Thus, following Colijn and Mackey (2005), we combined stem cells and early progenitor cells into one compartment and estimated their number as 1.55·10⁶ kg⁻¹.This excesses the estimate of the total body number of HSCs of 2·10⁴ that is currently adopted (Abkowitz et al. 2002, LeBien 2006). Radiosensitivity of HSCs and early progenitor cells is similar, and considering this compartment as being composed of homogeneous cells, we assigned a single value for the radiation-induced apoptosis rate for all cells in the compartment. These assumptions allowed us to describe hematopoiesis entirely by assigning parameter values that existed in the literature.

Two other effects not yet presented in the current version of the model are age-specific effects in hematopoiesis and late stochastic effects. The former are especially important for T-lymphopoesis. Biological effects are described in LeBien (2006), and the majority of these effects is included in the mathematical models of Romanyukha and Yashin (2003) and Sidorov et al. (2009). In this case the obtained characteristics of T-lymphopoesis represent those averaged over age. Since both the hematopoiesis model described in the present paper and the models of age-effects of T-lymphopoiesis are formalized in terms of differential equations, both models can be combined after adopting a hypothesis allowing to dynamically relate the components of the model.

An approach allowing for a description of the relationship between deterministic reactions of hematopoiesis and late stochastic effects will define the future direction of model development (outlined in Akushevich et al., 2010). This is discussed below in a separate subsection.

Properties of the developed model

The model presented here allows for an analytical solution of a new steady state, i.e., the steady state achieved under stationary chronic IR exposure. The solution found is not exact but was obtained by expansion of the exact solution as a power series over dose characteristics. Comparison of the exact solution obtained as a solution of the system of delay differential equations demonstrates the good quality of the applied approximation.

The effect of dose rate is given by Eq. (4) for the HSC compartment, and by Eqs. (5,6) for the peripheral blood lines. The main contribution to a blood count decline is proportional to the reciprocal of D₀ (the dose required to reduce cell survival to 37%). Since the values of D₀ for peripheral blood are large (except for lymphocytes), terms with D_0Q(Q ∈ {N, P, R}) in denominators can be neglected. Both dose-rate and cumulative dose effects represent the sums over all blood lines. Weights of contributions of specific blood compartments are proportional to the dimensionless factors d̅_Qκ_Q*τ_Q. Thus, the blood count declines are proportional to the fraction of HSC differentiated in the respective direction, κ_Q*, and maturation time, τ_Q. Since both these terms are responsible for the number of differentiated (and maturated) cells of the respective blood line under risk, their appearance in the formulae is clear.

The model includes parameters describing the hematopoietic system itself, and parameters responsible for effects of radiation exposure. The parameters of the first type are estimated using available information from animal experiments and human studies. Partly, similar information is also available for the second type of parameters (e.g., for D₀ ’s). However, model descriptions (e.g., by the one-hit-one-target theory) or experimental information from Akleyev et al. (2010) must also be used for a complete specification of the second-type model parameters. The parameter estimation was done such that well-established parameters formed the basis, while those parameters for which information is lacking or minimal were estimated using the steady-state equations. Such an approach provides certain robustness in the model estimations and substantive results obtained using the model.

In Section “Experimental Results and Model Prediction” it is shown that the model allows description of experimental findings such as: i) the value of the slope of the dose-effect curves describing the hematopoietic inhibition due to chronic IR in the Techa River Cohort, ii) the delay of effects after chronic exposure and the accumulated character of the effect, and iii) the dose rate patterns of the fractions of cytopenic states (e.g., leukopenia,. thrombocytopenia). All these finding were documented in Akleyev et al (2010) and their further analysis by means of the developed model allowed us to reveal and specify their certain properties. For example, time-patterns of the delay in dose-rate effects could be reconstructed, which was difficult to reconstruct using pure statistical methods of data analyses (because of the high correlation between dose rate and cumulative doses), and investigated using different model distributions (e.g., Weibull).

Dose Rate and Cumulative Dose Effects

Two types of effects due to radiation exposure are implemented into the model. The first is the dose rate effect corresponding to cell damage resulting in interphasic (hours) or mitotic (days) cell death. This effect is proportional to the current dose rate of the chronic exposure. The second is the effect of accumulated dose. This effect is related to non-lethal cell damages resulting in the increase of the number of injured cells. We referred to this effect as effect of cumulative dose; however, as already demonstrated, only few past years of exposure contribute to the observed blood cell decline. The effect of suppression of HSC proliferation (−β̅), which is proportional to the number of injured cells, is also proportional to the accumulated dose. The possibility to model the dose rate and cumulative dose effects separately is supported by available data on individual exposure history in the form of sets of annual dose rates at the year of measurements and years prior the year of measurements till the onset of IR exposure. Biological effects of dose rate during the year of measurement and dose rates during preceding years might be essentially different; therefore different model specifications were made for both effects and implemented into the model.

It was found that the dose rate effect can explain only 10% and 5% of the total declines in blood lines observed by Akleyev et al. (2010) for lymphocytes and all other blood lines, respectively, while cumulative dose effects may explain the remaining 90% and 95%, respectively. All parameters of the model for the dose rate effect were obtained using values known from other measurements. This fact allows for identification of dose rate and cumulative dose effects in the presented model. The relative fractions of the dose rate and cumulative dose effects observed in the present study allows for the following conclusion: The higher overall impact of the cumulative dose compared to the dose rate on the inhibition of hematopoiesis, together with the delayed realization of the cumulative dose effect, implies that non-lethal cell damage is the most common immediate response to IR, and that accumulation of such damage in a chronically exposed cell leads to its death or irreversible growth arrest with a substantial time lag after the end of the exposure.

Note that the evaluated fractions of dose rate and cumulative dose effects could be influenced by any future generalization of the model such as i) using models of lethal cell damages beyond the one-hit-one-target theory, ii) generalizations to capture non-targeted effects of IR, and iii) applying the new recently-issued (TRDS-2009, Degteva et al, 2010) Techa River Dosimetry System.

Long-Term effects and carcinogenesis models

The effect of chronic exposure to IR on hematopoietic and other radiosensitive tissues is dual. On the one hand, IR influences the kinetics of the cell populations during the early period of exposure resulting in deterministic effects. On the other hand, IR initiates and promotes stochastic late effects. Both types of effects are related, and this relationship has to be reflected in the developed models. In a recent report (Akushevich et al., 2010) it was demonstrated how the model of deterministic effects can be joined to a model of late stochastic health effects. The main stochastic effect of chronic exposure to IR in hematopoietic system is leukomogenesis.

The concepts and biological principles of a model of carcinogenesis that has a mathematical structure which allows for a combination with a deterministic model of hematopoiesis were recently presented by Veremeyeva et al. (2010a). The model is based on the concept of breaking barrier mechanisms and describes carcinogenesis as a dynamic trade-off between two antagonistic forces (or processes) promoting or hindering carcinogenesis at its different stages (initiation, promotion, conversion). Mathematically, the model is based on a stochastic process model known in biodemography (Yashin et al. 1985, Yashin and Manton, 1997). Properties of such an approach were reported by Akushevich et al. (2008).

However, since the dynamics of intracellular barriers is modeled at the level of HSC and since the characteristics of barrier breaking are measured at the level of peripheral blood, these two levels must be linked in a correct model of the stochastic effect. Such linkage can be provided if the components of the model of stochastic effects are dynamically related to the components of, and the model of, deterministic effects presented in Fig. 1. Furthermore, such a linkage allows for a description of the relationship between early deterministic reactions of hematopoiesis to chronic IR exposure and late stochastic effects such as leukemia recently reported by Veremeyeva et al. (2010b).

Population Model

The model presented in Fig. 1 and formalized by means of the delay differential equations in Eqs. (1) can serve as a basis for the construction of a population model capable of simulating individual trajectories in the space of blood counts. Figure 6 shows, as an example, the correlation between current blood counts and their annual rates. Two effects are immediately seen from these plots. The first is the negative feedback of the hematopoietic system enforcing blood counts to return to their normal values. The second is the stochastic component resulting from multiple (random) factors each of which cannot be taken into account individually. Respective population models were recently further developed by Yashin et al. (2007, 2008). In the case of linear feedback and Gaussian stochasticity the model has the following form

$$dc=-a(c-f_1)dt+bd{W}_t$$

and can be solved analytically (i.e., distributions for individual trajectories can be reconstructed without additional assumptions). Here, c is the vector of blood counts, a is the matrix providing negative feedback, f₁ is a vector representing the so-called effect of allostatic load (it defines the value in blood count space for which blood counts would converge in the absence of the stochastic component, bdW_t), b is the matrix describing the magnitude of the stochastic component, and W_t refers to the Wiener process.

Fig 6.

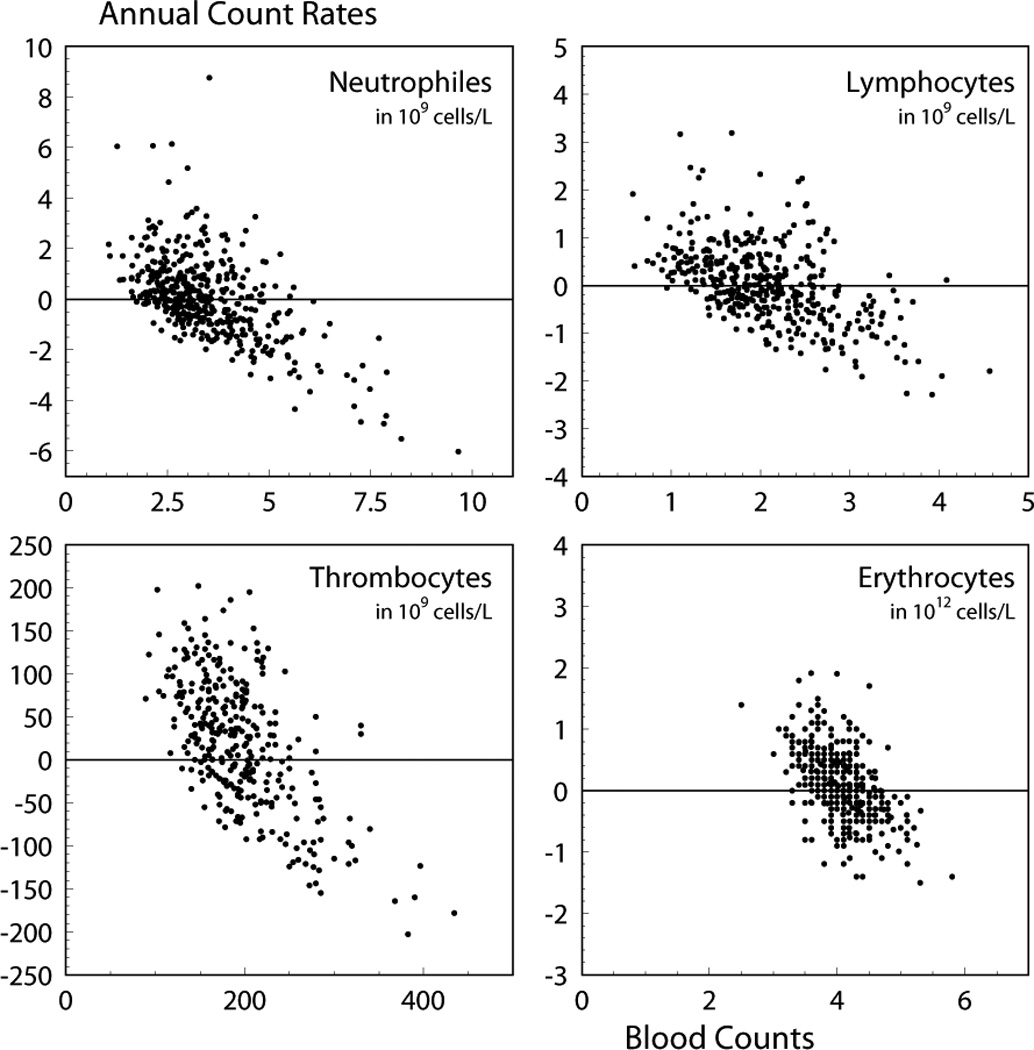
Annual change in blood counts relative to their values at the beginning of the annual time interval. Units for specific blood lines are given in the respective plots.

In the general case, the deterministic component in this equation is not linear in blood count c and is modulated by the effects of IR. It is described by Eqs. (1). Thus, the population model for hematopoiesis under chronic irradiation can be constructed using Eqs. (1) for the deterministic component of the population model and the stochastic component. Generalization of the model in this way will allow to investigate the processes of recovery, which may depend on an individual and include individual radiosensitivity.

Conclusion

The developed model of hematopoiesis is characterized by clear analytical and statistical properties. The majority of model parameters can be estimated using information available from the literature. The model is capable of describing recent empirical findings on the dynamics of hematopoietic factors under chronic exposure to IR. The broad spectrum of potential applications of the model includes: i) further investigation of health effects induced by IR, e.g., carcinogenesis or differential reactions of radiosensitive tissues, ii) development of strategies of radiation protection through calculating the risks for specific population groups, and iii) investigation of normal tissue reactions during radiological treatment, in radiation oncology. The model can be further generalized for i) predicting the early effects of chronic exposure to IR such as the level of hematopoietic inhibition and the dynamics of subsequent recovery after the end of exposure, and ii) estimating the risks of late stochastic effects performed not only on the basis of the exposure characteristics (dose, dose rate) but also by taking into account the early individual reactions to exposure during the initial exposure period. The prognoses obtained by the model can be used for elaborating preventive measures in emergency situations involving IR exposure of large population groups.