Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Nov 18;3:3238. doi: 10.1038/srep03238

From Boron Cluster to Two-Dimensional Boron Sheet on Cu(111) Surface: Growth Mechanism and Hole Formation

Hongsheng Liu 1, Junfeng Gao 1,2, Jijun Zhao 1,2,a
PMCID: PMC3831238  PMID: 24241341

Abstract

As attractive analogue of graphene, boron monolayers have been theoretically predicted. However, due to electron deficiency of boron atom, synthesizing boron monolayer is very challenging in experiments. Using first-principles calculations, we explore stability and growth mechanism of various boron sheets on Cu(111) substrate. The monotonic decrease of formation energy of boron cluster BN with increasing cluster size and low diffusion barrier for a single B atom on Cu(111) surface ensure continuous growth of two-dimensional (2D) boron cluster. During growth process, hexagonal holes can easily arise at the edge of a 2D triangular boron cluster and then diffuse entad. Hence, large-scale boron monolayer with mixed hexagonal-triangular geometry can be obtained via either depositing boron atoms directly on Cu(111) surface or soft landing of small planar BN clusters. Our theoretical predictions would stimulate further experiments of synthesizing boron sheets on metal substrates and thus enrich the variety of 2D monolayer materials.

Since the first experimental isolation of graphene by Novoselov and Geim in 20041, there have been tremendous interests in the two-dimensional (2D) monolayer materials of only one-atom thickness2,3, such as h-BN sheet and silicene. Among them, graphene and silicene constitute a special kind of semimetals with Dirac cones at the Fermi level4,5,6, whereas infinite h-BN sheet is a wide-band-gap semiconductor7. Certainly, the diversity of physical properties of these 2D monolayers is crucial for their wide applications in future nanoscale materials and devices.

On the periodic table, boron is the neighbor of carbon with three valence electrons in the 2 s and 2 p orbitals; thus it is able to form sp2 hybridization like carbon. Intuitively, boron atoms are expected to form fullerene-like cage configurations and graphene-like monolayer sheet. In 2007, Yakobson's group8 predicted a very stable B80 fullerene cage analogous to C60 buckyball. However, hollow cages are indeed not the ground state structures for the medium-sized BN clusters from N = 68, whereas core-shell configurations are more thermodynamically preferred based on ab initio global search by our group9,10 and others11,12. The energetic unfavorability of these empty boron cages can be attributed to the electron deficiency of boron, which tends to adopt more compact structures.

Stimulated by the B80 fullerene cage, a 2D boron sheet (BS), namely “α-sheet”, with appreciable stability was constructed13,14,15. By incorporating periodic hexagonal holes in the triangular lattice to reach the balance between three-center (3c) and two-center (2c) bonds, this mixed hexagonal-triangular boron sheet (ht-BS) is more stable than previously proposed buckled triangular boron sheets (t-BS)16,17,18,19, which can be explained by a chemical bonding picture that the hexagon holes serve as scavengers of extra electrons from the filled hexagons20. There have been some recent activities of searching more stable structure for 2D allotropes of boron, including the snub-sheet, g1/8-sheet, g2/15-sheet, α1-sheet, β1-sheet, struc-1/8-sheet21,22,23,24. All these ht-BSs can be constructed by carving different patterns of hexagonal holes within the triangular sheet and described by a hexagon hole density η, defined as the ratio of number of hexagon holes to the number of atoms in the original t-BS.

These boron monolayers of abundant structures certainly bring new members to wonderful 2D atomic films and provide novel building blocks for nanoscale materials and devices. But monolayer BS has not been experimentally synthesized yet due to the electron deficiency of B atom. In previous experiments25,26, single-walled and multi-walled boron nanotubes have been observed, which hints the possible existence of boron monolayer sheet since a boron sheet can be viewed as unrolling a boron nanotube. With metal passivation to stabilize the sp2 hybridization, similar silicene monolayer has been successfully fabricated on Ag(111) and Ir(111) surfaces in recent experiments6,27,28,29,30, providing important clues for BS synthesis. On the other hand, small boron clusters in vacuum were proved to adopt quasi-planar configurations31,32,33,34,35,36,37, which may act as precursors for experimental synthesis of BS on metal surface via soft-landing of cluster beams38.

As experimentalists have to spend lots of money and time by testing numerous metal substrates and various growth conditions, it would be instructive to investigate the synthesis of BSs on metal surfaces from the theoretical aspect. Recently, Zhang and co-workers39 proposed boron monolayers can keep their structures with slight buckling on several metal surfaces based on theoretical exploration. Using first-principles simulations, Yakobson's group suggested that stable BS with a certain density of hole can be derived by the deposition of B atoms on Au and Ag surface or saturation of B-terminated MgB2 surface in a B-rich environment40.

Typical epitaxial growth of a boron sheet on metal surface can be divided into three stages: (i) a certain amount of BN clusters form on metal surface by aggregation of B atoms or soft landing of these BN clusters; (ii) BN clusters keep growing into pieces of BS sheet by attaching more and more isolated B atoms; (iii) further annealing to achieve stable monolayer structure and to remove defects. As ht-BS is more stable than t-BS, the final stage would be important for reaching the optimal density and pattern of holes in ht-BS. Although previous theoretical simulations39,40 have made certain progresses, some fundamental mechanisms of BS growth still have to be clarified. For example, what is the most stable configurations for the BN clusters on a specific metal surface at the initial stage of BS growth? How do B atoms attach to the edges of a seed BN cluster? How do the holes form and assemble into patterned ht-BS? If various BSs have grown on metal surface, how to identify and distinguish them using experimental means?

To address these critical issues, here we investigate the equilibrium geometries and interaction mechanism of boron clusters and sheets on Cu(111) surface using comprehensive first-principles calculations. Similar to the free-standing sheets, ht-BSs on Cu(111) surface energetically prevail against both t-BS and h-BS. Interestingly, the embryo of ht-BS structural motif emerges as early as B11 cluster on Cu(111) surface and competes with those from t-BS motif. Moreover, boron atoms tend to congregate on Cu(111) surface with small diffusion barrier to form 2D clusters. During growth of these 2D clusters with triangular networks, hexagonal hole can easily occur and migrate, which promotes the formation of ht-BS on Cu surface. Our theoretical results provide valuable guidance of how to achieve 2D boron sheets in future experiments.

Results

Boron monolayer on Cu(111) surface

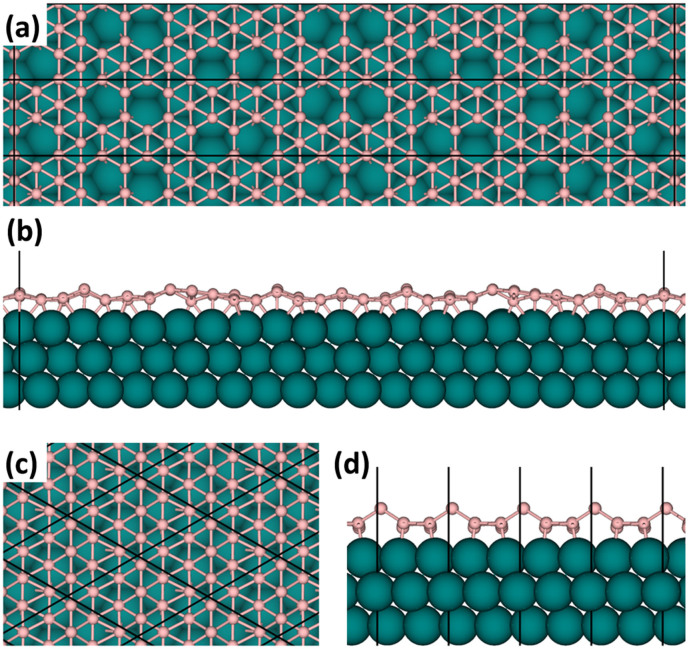
The atomic structures for various boron monolayer sheets on Cu(111) systems are illustrated in Figure 1 and Figure S1 in the Supporting Information. After relaxation, the BSs with slight buckling retain their elementary geometries, implying possible existence of planar boron structures on Cu substrate. The amplitudes of the buckled height h, defined as the vertical distance between the highest and lowest boron atoms with regard to the Cu surface, were calculated for eight types of BS considered and summarized in Table 1. For all ht-BSs, the buckled heights are around 1 Å, comparable to that for silicene on Ag(111)41. Meanwhile, the buckled height is 1.2 Å for the triangular sheet, which is slightly larger than those for ht-BSs. In addition, we measured the average distance d between boron atoms and Cu substrates. As shown in Table 1, the average B-Cu distance ranges between 2.1 Å and 2.2 Å, which is comparable to that in the known B-Cu alloys (2.1 ~ 2.2 Å)42 and suggests moderate covalent bonding interaction between boron and copper atoms. The buckled geometries and various hole distributions of BSs on Cu(111) surfaces may increase the difficulty to identify their structures. To help experimentalists distinguish different BS monolayers in the future, here we provided simulated scanning tunneling microscope (STM) images for typical BSs on Cu(111) surface (see Figure S2 of Supporting Information).

Figure 1. Atomic structures of two representative boron monolayers on Cu(111) surface.

Figure 1

Open in a new tab

(a), (b): g2/15-sheet; (c), (d): triangular sheet. (a), (c): top views; (b), (d): side views.

Table 1. Structural and energetic parameters for eight boron sheets supported on Cu(111) substrate. QB is the average charge per boron atom in the BSs (see text for the definition of other parameters).

Boron sheets η Eformvac (eV/atom) Eform (eV/atom) Ec (eV/Å2) h (Å) d (Å) QB (e)
g2/15-sheet 2/15 0.396 0.207 0.066 0.82 2.18 −0.043
g1/8-sheet 1/8 0.393 0.220 0.061 1.09 2.20 −0.044
α-sheet 1/9 0.395 0.226 0.053 0.88 2.14 −0.047
β1-sheet 1/8 0.413 0.232 0.064 1.04 2.21 −0.040
snub-sheet 1/7 0.417 0.232 0.056 0.91 2.13 −0.042
α1-sheet 1/8 0.399 0.239 0.057 0.98 2.20 −0.042
struc-1/8-sheet 1/8 0.399 0.246 0.054 0.99 2.21 −0.040
triangular sheet 0 0.709 0.338 0.127 1.21 2.39 −0.026
Open in a new tab

The formation energies for various BSs in vacuum and on Cu(111) surface are summarized in Table 1. Compared to the standalone sheets, the formation energies of boron monolayers on Cu(111) surface are reduced by about 0.2 eV/atom, indicating that Cu substrate can stabilize BSs, similar to the Ag(111)-supported silicene sheets41. On Cu(111) surface, the most stable BS is the g2/15-sheet with Eform = 0.207 eV/atom, while the g1/8-sheet and α-sheet are also rather stable with only 0.013 eV/atom and 0.019 eV/atom higher in energy. Indeed, these three isoenergetic ht-BSs, obeying the rule of 1/9 ≤ η ≤ 2/1522, are the most favorable ones in vacuum13,22. Also note that the formation energy of the fully triangular sheet on Cu surface is 0.338 eV/atom, higher than the most stable g2/15-sheet by 0.131 eV/atom. Such noticeable energy difference between ht-BS and t-BS would provide the driving force for structural transformation from fully triangular to mixed hexagonal-triangular sheets, as we will discuss in the Section 3.3 below. Test calculations with DFT-D2 method43 for three typical boron sheets on Cu surface have also been performed and showed that inclusion of dispersion correction only lead to a systematical shift (about 0.023 eV/atom) of formation energies without changing the energetic sequence of different sheets. Therefore, standard GGA-PBE method is sufficient for describing the relative stability of the present systems.

Using the structures reported in our previous study41 and the present theoretical scheme, the calculated formation energy of silicene on Ag(111) surface is about 0.2 eV per silicon atom, which is comparable to that for various ht-BS on Cu(111) surface. In recent years, silicene has been successfully synthesised on various metal substrates6,27,28,29,30. Thus, we anticipate that boron sheet may also be synthesized on metal surface with the method similar to that for silicene synthesis. In nature, however, there is no boron allotrope with layered structure analogy to the graphite. The bulk phases of boron solids (such as α-boron and β-boron) are mostly based on basic unit of B12 icosahedron44. To compare the mixed hexagonal-triangular boron sheets (ht-BSs) with a dense 2D arrangement of icosahedra, a monolayer composed of B12 icosahedra on Cu(111) surface was constructured (Figure S2). Using the same theoretical scheme, the formation energy of Cu-supported B12-based sheet is 0.214 eV per boron atom, which is almost energy degeneracy with the most stable ht-BSs (see Table 1). This result clearly indicate that the boron thin film would eventually become bulk-like composed of B12 icosahedra if enough boron atoms are deposited on Cu surface. Note that their atomic densities of boron on Cu(111) surface are different, i.e., 0.56 Å−2 for B12 icosahedron sheet and 0.35 Å−2 for ht-BSs respectively. Therefore, in order to achieve boron monolayer, the amount of boron atoms deposited on Cu substrate must be strictly controlled within a small value (about 0.35 atom per Å2).

Moreover, using the structures reported in our previous study41 and the present theoretical scheme, the differences in formation energies of different silicene@Ag superstructures are about 0.03 eV/atom, which are comparable to that for various mixed hexagonal-triangular boron sheets on Cu surface (about 0.02 ~ 0.03 eV/atom, see Table 1). In experiments, coexistence of various silicene@Ag superstructures has been observed28,45. Consequently, the final boron sheet synthesized on Cu surface might be a 2D polycrystalline as a mixture of these ht-BS domains, i.e., different patterns of hexagonal holes on the filled triangular lattice.

The adhesion strength between ht-BSs and Cu(111) surface can be directly measured by the Ec defined by Eq.(6), which ranges between 0.053 and 0.066 eV/Å2 (see Table 1). According to Bader charge analysis, each boron atom gains only about 0.04 electrons from Cu substrate. This can be attributed to the small electronegativity difference of these two elements (2.04 for B and 1.90 for Cu according to Pauling's definition). Such moderate B-Cu interaction would be beneficial for stripping boron monolayer films from Cu substrate, which is a necessary step for future utilizations of the 2D boron materials. In addition, the lowest-energy configurations of ht-BSs on Cu(111) surface, i.e., g1/8-sheet, g2/15-sheet, α-sheet, are also the most energetically favorable ones in vacuum. Therefore, once an as-prepared boron sheet is stripped from Cu substrate, it can stand alone and remain stable during the transfer process between different substrates.

It is known that the graphene-like honeycomb lattice of boron is unstable in vacuum due to electron deficiency46. Since the Cu-to-B charge transfer is too small to remedy the electron deficiency of boron, the h-BS cannot survive even on Cu(111) surface and will collapse into a disordered sheet with triangular domains and large voids (see Figure S1(m, n) of Supporting Information). This result is in accordance with previous finding by Yakobson's group40 but in contrary to the prediction by Zhang et al.39, who suggested that h-BS on some metal surfaces (Mg, Al, Ti, Au, Ag) is more favorable than both t-BS and ht-BS. This difference might be attributed to stronger BS-substrate interactions (about 0.6 ~ 1.2 eV/atom) from Zhang's calculations.

In real experiments, boron monolayer must be synthesized at finite temperatures, where thermal perturbation may introduce some structural defects and thus disturb the geometry integrity of 2D atomic sheet41. To examine the thermal stability of boron sheets on Cu surface, we preformed ab initio molecular dynamics (AIMD) simulations for α-sheet on Cu(111) surface as a representative. Using VASP code, AIMD simulations were carried out at 500 K and 800 K with time step of 1 fs. At both temperatures, no topological defect was ever generated during the entire simulation time of 6.5 ps (Figure S3), confirming the high thermal stability of boron sheets on Cu(111) surface.

Structures of boron clusters on Cu(111) surface

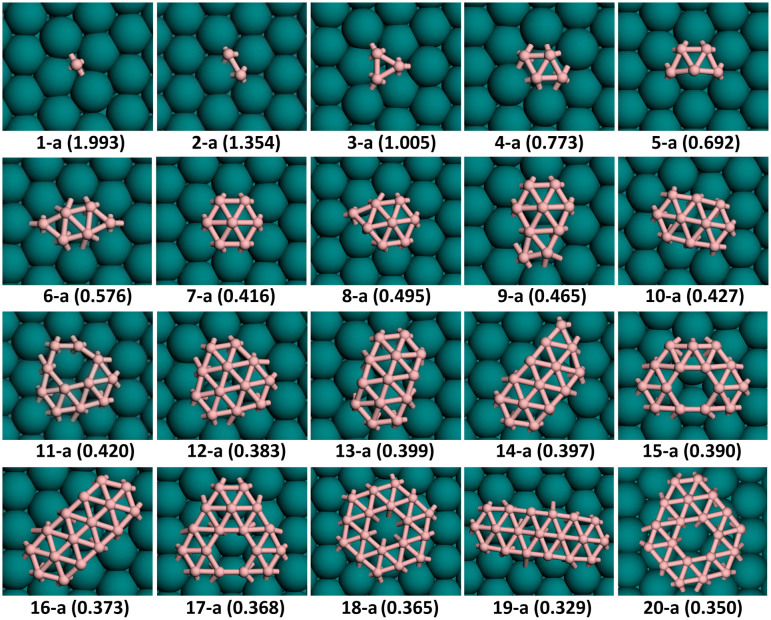
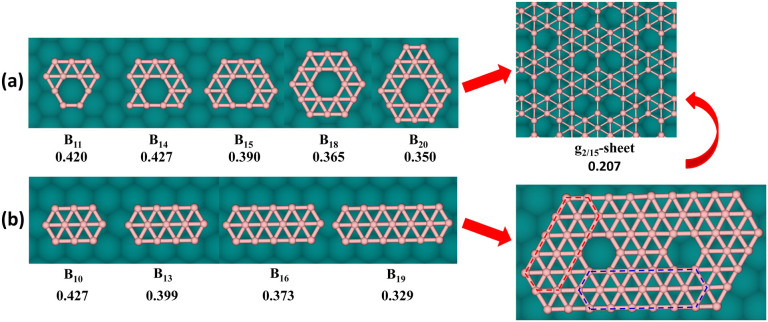
From the above discussions, one can see that various ht-BSs are all stable on Cu(111) surface. To further elucidate the growth behavior and nucleation mechanism of boron sheets, it is thus necessary to explore the geometries and stabilities of small boron cluster on metal substrate, as we did before for graphene and silicene clusters on metal surfaces41,47,48,49. Several critical issues have to be addressed: (1) do small boron clusters prefer two-dimensional or three-dimensional structure on Cu surface? (2) what is the structural difference for boron clusters in vacuum and on metal substrate? (3) what is the correlation between cluster size and thermodynamic stability and is there any magic-sized BN cluster with particularly high stability? To answer these questions, the low-energy configurations and stability of small BN clusters up to N = 20 on Cu(111) surface were systemically investigated by DFT calculations. The ground-state structures of Cu-supported BN clusters are shown in Figure 2, and some selected isomers are presented in Figure S6 of Supporting Information.

Figure 2. Most stable configurations and formation energies (eV per boron atom, given in the parenthesis) of 2D BN clusters (N = 1–20) on Cu(111) surface.

Figure 2

Open in a new tab

To search the most stable configurations, we have constructed numerous structural isomers for each size of BN clusters on Cu substrate. At least five isomers were considered for N ≥ 9, whereas the number of isomers increases with the number of boron atoms, e.g., sixteen isomers for B19. According to our test calculations, the triangular networks embedded with quadrilaterals or pentagons (e.g., 9-b, 11-b, 13-d, 17-e and 19-d in Figure S6 of Supporting Information) have relatively higher formation energies and thus are not further considered. Due to the large number of possible conformations, we cannot exhaust all isomers for N > 10. Only planar structures composed of triangular units with or without hexagonal hole were considered, which can be viewed as the precursors of ht-BS and t-BS, respectively. In addition, some selected 3D clusters (e.g., icosahedron for B12, double ring for B20) were also placed on Cu(111) to examine the competition between 2D and 3D structures.

For a single boron atom adsorbed on Cu(111) surface, the most energetically favored position is the bridge site (see Figure 2), whose formation energy is 0.09 eV/atom lower than that of the hollow site. A boron adatom is unstable on the top site and would move to the bridge site upon relaxation. Hence, we tend to avoid the top sites and maximize the bridge sites when we constructed the initial geometries for Cu(111)-supported BN clusters. In the case of B2 dimer, however, two boron atoms sit on the hollow sites of Cu(111) surface with B-B distance of 1.60 Å since the nearest neighboring bridge sites are too close (1.28 Å) and the second nearest ones are too far (2.22 Å).

On Cu(111) surface, B3 is a regular triangle and B4 is a rhombus composed of two triangles. Chain configurations (3-b and 4-b in Figure S6 of Supporting Information) were also considered for B3 and B4, but are higher in energy by 0.049 eV/atom and 0.095 eV/atom, respectively. Hence, chain isomers were not considered for larger BN clusters with N > 4. The strong preference of 2D compact structures based on triangular units in BN clusters is distinctly different from CN clusters on Ni(111) surface, which prefer chain configurations up to N = 1147,48. This is simply because that boron does not adopt sp hybridization like carbon.

Following the triangular structural motif, the lowest-energy configurations of Cu(111)-supported B5 and B6 are trapezium and parallelogram composed of three and four triangular units, respectively. The hexagonal ring of B6 (6-b in Figure S6 of Supporting Information) is unstable with higher formation energy by 0.061 eV/atom, implying that an individual hexagonal boron ring does not exist on Cu(111) surface. An atom-centered hexagon emerges as the ground state of B7 on Cu(111). Interestingly, the most favored configurations for small BN clusters (N ≤ 7) on Cu substrate are all identical to those in vacuum34 (see Figure S5 of Supporting Information for the ground state structures of gas-phase boron clusters).

The ground state structures of gas-phase B8 and B9 clusters are atom-centered heptagon and octagon (Figure S5), respectively34. On Cu(111) surface, however, the wheel structures for B8 and B9 are unstable and would transform to B7-based triangular networks, i.e., atom-centered hexagons with one or two atoms on the edge. This suggests that the maximum coordination number of boron atom in the metal-supported clusters or monolayer sheet cannot exceed six. As for B10, the lowest-energy geometries in vacuum and on Cu surface are identical, i.e., a belt-like configuration with regular triangular network. Clearly, the most stable structures of small BN clusters (3 ≤ N ≤ 10) on Cu(111) surface are all made up of triangular units, which can be considered as embryo of t-BS.

On Cu(111) substrate, B11 is the first cluster with triangular network consisting of a hexagonal hole, which can be regarded as a precursor of ht-BS. By contrast, the gas-phase B11 configuration is constituted by nine triangle units and one quadrilateral35. A 2D closed-shell structure with C3V symmetry, consisting of thirteen triangles, is the ground state for both gas-phase34 and Cu-supported B12. To examine possible existence of 3D structures, B12 icosahedron was placed on Cu(111) surface (12-c in Figure S6 of Supporting Information); but its formation energy is much higher than the 2D C3v configuration by 0.444 eV/atom. Thus, an individual icosahedron (which is the basic structural unit of boron solids) cannot occur on Cu(111) surface. In previous calculations by Yakobson's group40, B12 icosahedron on Ag(111) surface was also energetically unfavorable with regard to the planar structure by 0.225 eV/atom.

Similar to B10, B13 on Cu(111) surface also adopts belt-like configuration with triangular network. In vacuum, the same structure was found for anionic B13− cluster34, but not for neutral B13. This can be explained by the saturation effect of metal surface since that B13 cluster gains about 1.2 electrons from Cu substrate according to Bader analysis. The lowest-energy geometry of B14 is also belt-like simply by adding one atom to the B13 belt (13-a in Figure 2). The isomers as pieces of ht-BS were also considered for B13 and B14 (13-e and 14-c in Figure S6 of Supporting Information), but their energies are higher than the belt structures by 0.058 eV/atom and 0.030 eV/atom, respectively.

In the case of B15, ht-BS structural pattern prevails again and its lowest-energy geometry is based on 14-c isomer of B14 with one additional atom on the rim, forming a C2v structure with a hexagonal hole symmetrically surrounded by thirteen triangles. Following B10 and B13, B16 adopt belt-like triangular network (16-a in Figure 2) as its ground state both on Cu surface and in vacuum. Meanwhile, 16-b isomer (Figure S6 of Supporting Information) with one hexagonal hole is less stable by 0.036 eV/atom probably due to the two-coordinated boron atom on top of 15-a configuration.

As a continuation of ht-BS motif, the lowest-energy structure of B17 on Cu(111) substrate can be obtained by adding a boron dimer on top of 15-a configuration, preserving C2v symmetry. Interestingly, it can be regarded as a fragment of every ht-BS considered here except the snub one. Similarly, B18 prefers a triangular network with a hexagonal hole in the center and possesses a high symmetry of C6V. This planar boron patch also exists in most ht-BSs except g2/15-sheet and β1-sheet. The 18-c isomer as a full triangular network with D3h symmetry, which is the ground state in vacuum, is higher in energy by 0.027 eV/atom on Cu surface. At N = 19, the triangle-based belt configuration prevails again and its energy is lower than the 19-b isomer of ht-BS motif (Figure S6 of Supporting Information) by 0.038 eV.

The most stable structure of B20 on Cu surface can be obtained by adding two boron atoms to the 18-a configuration, resulting in C2v symmetry. Again, it can be viewed as a fragment of g1/8-sheet, α-sheet, α1-sheet, and struc-1/8-sheet. For comparison, the 3D double-ring tubular structure (20-e in Figure S6 in Supporting Information), which is the ground state of B20 in vacuum33, is energetically unfavorable on Cu surface with ΔE = 0.073 eV/atom, simply because only half of boron atoms interact with Cu atoms. The high formation energies of B12 icosahedron and B20 double-ring clearly indicate that 3D structures are not favored on Cu(111) surface.

From the above results, we can derive some general trends about the structures and growth patterns for small boron clusters on Cu(111) surface. First, all Cu-supported BN clusters prefer 2D configurations rather than 3D ones. Such 2D preference is certainly a prerequisite for fabricating boron monolayer films on metal substrates. At cluster sizes of N = 3, 4, 5, 6, 7, 10, 12, 16, the lowest-energy geometries of BN in vacuum (highlighted in Figure S5 of Supporting Information) and on Cu surface are identical and they are all symmetric triangular networks. However, this kind of geometries cannot form in the B11, B13, B15, B17 and B19 clusters; a quadrilateral has to be included in the gas-phase configuration to reduce the number of low-coordinated boron atoms. When supported on Cu(111) substrate, a hexagonal hole instead of a quadrilateral is formed inside the triangular networks of BN clusters. These structures can be considered as the early stage of ht-BS. Therefore, we infer that metal surface plays a significant role in occurrence of the boron sheets composed of triangular units and hexagonal holes (i.e., ht-BS).

For BN clusters with N ≥ 11, we observed strong competition between t-BS and ht-BS motifs. For those full triangular islands as precursors of t-BS, belt-like structures are more favorable and emerge at N = 10, 13, 14, 16, 19, whereas only B12 prefers an enclosed triangular network. On the other hand, in those lowest-energy triangular networks with hexagon hole (11-a, 15-a, 17-a, 18-a and 20-a in Figure 2), the hexagons are always well embraced by triangular units. We further constructed several belt-like configurations incorporated with one hexagonal hole (12-b, 15-b and 18-b in Figure S6 of Supporting Information) and 2D triangular networks with two hexagonal holes (14-d and 16-e in Figure S6 of Supporting Information). All of them were found to be energetically unfavorable. Therefore, we can conclude that a hexagonal hole has to be enclosed by sufficient amount of triangles to achieve stable 2D boron cluster within ht-BS motif.

Interaction between boron clusters and Cu(111) surface

We first discuss interaction between 2D boron clusters and Cu(111) surface in terms of buckled heights (Figure S7 of Supporting Information). For three typical enclosed triangular boron clusters (12-a, 16-c, 19-e) as precursors of t-BS, the buckled height increases with increasing cluster size and reaches up to 1.32 Å at N = 19, compared to h = 1.21 Å for the infinite triangular sheet. The buckled heights for two representative hole-doped triangular boron clusters (17-a and 18-a) of ht-BS type are only 0.43 Å and 0.28 Å, respectively, much less than that of the infinite ht-BS (about 1 Å). The larger buckling in Cu-supported ht-BS is mainly caused by the mismatch of 2D boron lattice and Cu(111) surface. In contrast, small boron clusters without constraint of periodic boundary condition can accommodate Cu(111) surface better since the edge boron atoms have more degrees of freedom for adjusting their adsorption positions.

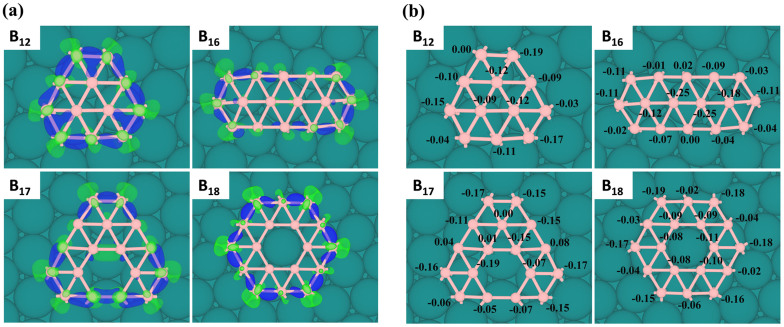
As illustrated by charge density difference (Figure 3a) and Bader charge analysis (Figure 3b), interactions between boron clusters and Cu(111) surface mainly occur on the periphery of boron clusters. Cu substrate causes depletion of in-plane σ states and accumulation of out-of-plane π electrons on the borders of boron clusters. The amount of electron transfer from Cu substrate to boron clusters is usually larger than that for boron monolayers (about −0.04 electrons per B atom). The larger electron transfer in Cu-supported BN clusters remedies the electron deficiency of boron and thus results in different equilibrium geometries from the gas-phase clusters.

Figure 3.

Figure 3

Open in a new tab

(a) Charge density difference and (b) on-site charge transfer from Bader analysis for four typical 2D BN clusters (N = 12, 16, 17, 18) on Cu(111) surface. In (a), electron accumulation is represented by green and electron depletion is represented by blue. In (b), the unit of charge transfer is |e|.

Previously, the extraordinary stability of free-standing α-sheet of boron were explained by the 3c-2e σ-bonds, 4c-2e σ-bonds, and delocalized π-bonds (6c-2e)20. Due to lack of periodic environment and the consequently unsaturated periphery atoms, BN clusters as small fragments of ht-BS, e.g., 17-a and 18-a, are not energetically favorable in vacuum but can be stabilized on Cu(111) surface. This can be understood by the following bonding picture. There are one 3c-2e σ-bond in each triangle and one delocalized π-bond in each hexagonal hole, respectively. On the other rim of supported boron clusters, the corner boron atoms form two bonds with metal substrate, while the other edge atoms form one bond. For example, B18 of 18-a configuration has eighteen triangles and one hexagon, which require 18 × 2 = 36 σ electrons and 2 π electrons. On the periphery of B18, each of the six corner B atoms forms two bonds with Cu atoms, and each of the six edge B atoms forms one bond, respectively. Hence, totally 56 electrons are needed to fulfill all these bonds. Indeed, eighteen boron atoms can offer 54 electrons and the entire B18 cluster gains about 1.8 electrons from Cu surface according to Bader analysis, making the total number of electrons near 56. Clearly, passivation effect by metal surface and charge transfer from metal to boron account for stabilization of the ht-BS patches.

Implication on the growth behavior of boron monolayer

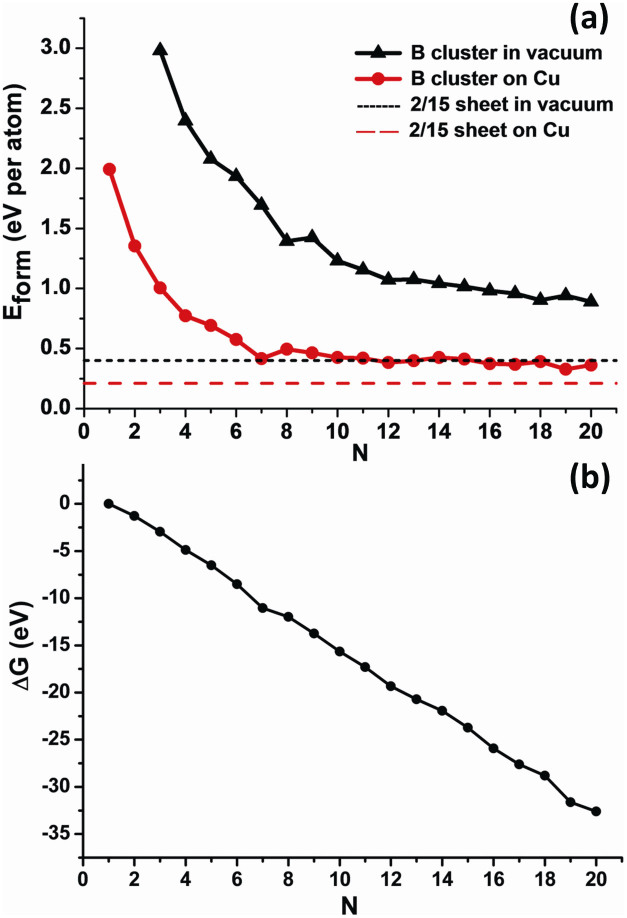
Figure 4 plots formation energies of free-standing and Cu-supported BN clusters as function of size N. Due to metal passivation, the formation energies of BN clusters are significantly reduced from vacuum to Cu(111) surface, especially for those small clusters. For example, the difference of formation energies for systems before and after adsorbed on Cu(111) surfaces is 1.359 eV/atom for B6 and 0.5 ~ 0.7 eV/atom for N = 12 ~ 20, respectively. As clusters further increases, it eventually reaches about 0.15 ~ 0.19 eV/atom for infinite ht-BSs (see Table 1 and Figure 4), e.g., 0.188 eV/atom for g2/15-sheet. Again, this indicates that large boron sheets interact with Cu substrate more weakly than small BN clusters, in line with above charge analysis. It is noteworthy that the cohesion strength between various boron sheets and Cu(111) surface is the same magnitude of graphene on Cu surfaces (about 0.022 eV/Å2)50, implying that the as-fabricated ht-BSs may be peeled off from metal substrates like graphene.

Figure 4.

Figure 4

Open in a new tab

(a) Formation energies of the most stable BN clusters and boron sheet in vacuum and on Cu(111) surface. (b) The Gibbs free energy of Cu supported boron clusters as a function of cluster size.

Within the explored size range, the formation energy of BN clusters decreases as N increases both in vacuum and on Cu(111) surface, excepted for some highly stable sizes. Supposing boron atoms are directly deposited on Cu(111) surface, the growth process of a monolayer boron sheet can thus be viewed as a phase transition from dispersed boron monomers to 2D sheet with patterned structures. Therefore, the chemical potential of various BSs on Cu(111) at 0 K can be computed by:

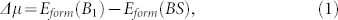graphic file with name srep03238-m1.jpg

where Eform(B1) = 1.993 eV/atom is the formation energy of boron monomer on Cu(111) surface, Eform(BS) is the formation energy of boron sheet on Cu(111) surface, which lies between 0.207 eV/atom and 0.338 eV/atom. Thus the value of Δμ changes from 1.786 eV/atom to 1.655 eV/atom for various patterned structures of BSs on Cu(111) surface.

Using chemical potential defined in Eq.(1), the Gibbs free energy of boron clusters on Cu(111) surface can be calculated51 by

graphic file with name srep03238-m2.jpg
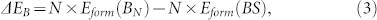graphic file with name srep03238-m3.jpg

where N is the number of boron atoms in cluster, Eform(BN) is the formation energy of boron cluster, Eform(BS) is the formation energy of infinite boron sheet. As displayed in Figure 4b, the Gibbs free energy BN cluster is always negative and decreases monotonously with increasing cluster size N, which implies spontaneous aggregation of boron atoms and incessant growth of boron cluster on Cu(111) surface at normal conditions. In comparison, on Ag(111) surface, ΔG slowly decreases with increasing cluster size even for small Δμ = 0.2 eV/atom and the nucleation barrier is about 3 eV40.

Besides, some BN clusters (e.g., B7, B10, B12 and B16) exhibit high stability on Cu substrate from the second derivatives of the formation energies (see Figure S8 of Supporting Information), and they possess the same planar structures as in vacuum. Therefore, these boron 2D clusters can be directly soft-landed on Cu(111) surface using cluster beam apparatus38 as nucleation seeds for further growth of various boron sheets.

In principle, boron sheets on Cu(111) surfaces can be obtained via continuous growth of small clusters or coalescence of them. According to our calculations (Figure S9 of Supporting Information), the diffusion barrier of isolated B atoms on Cu(111) is only 0.141 eV. Therefore, the continuous growth of 2D boron clusters is guaranteed by the negative ΔG and low diffusion barrier. To schematically show how a ht-BS forms on metal surface, in Figure 5 we propose two possible growth pathways based on lowest-energy or metastable configurations of BN clusters. In the path (a), starting from N = 11, small BN clusters with hexagonal-hole-doped triangular lattice occur on Cu surface as nucleation centers of ht-BS. As boron atoms aggregate around the BN cluster, the hexagonal hole is completely surrounded by triangular units at B18. Afterwards, more boron atoms will accumulate around B18, e.g., a B2 dimer on top of B18 leading to B20. Although larger BN clusters (N > 20) are not explored due to restriction of computing resource, one can naturally anticipate formation of more and more hexagons inside the triangular network of a 2D BN cluster as it grow bigger, finally coming into being macroscopic monolayer of ht-BS.

Figure 5. Schematic plots for two possible growth paths of ht-BS (g2/15-sheet as representative) from small BN clusters.

Figure 5

Open in a new tab

Formation energies in unit of eV per boron atom are given below the name of boron clusters and sheet.

As shown in the path (b) of Figure 5, boron nanoribbons may also serve as building blocks of ht-BS. Since the belt-like BN clusters (i.e., B10, B13, B16, B19) with regular triangular lattices are very stable, many nanoribbons of finite length may exist during the initial stage of growth. When several boron ribbons aligning in different orientations merge with each other, a hexagonal hole may occur via either directly enclosing of three nanoribbons with well-defined intersection angle of 120° or diffusion of few boron atoms (see discussion below for the formation mechanism of hexagonal hole).

Is it possible to grow a boron monolayer fully with triangular lattice on Cu substrate? B12 as a possible precursor of t-BS (12-a in Figure 2) is rather stable on Cu(111) surface. However, as the cluster becomes bigger, these enclosed triangular structures resembling B12 (14-b, 16-c and 19-e in Figure S6 of Supporting Information) become less favorable. The 19-e isomer with a triangular network of C6V symmetry forms a dome-like shape on Cu surface similar to graphene patch49,52, and its formation energy is 0.121 eV/atom higher than the 19-a ground state. The higher formation energies of enclosed triangular boron clusters originate from their larger buckled height h, which are shown in Figure S7 of Supporting Information (B12, B16 and B19), and prevent formation of triangular boron sheet.

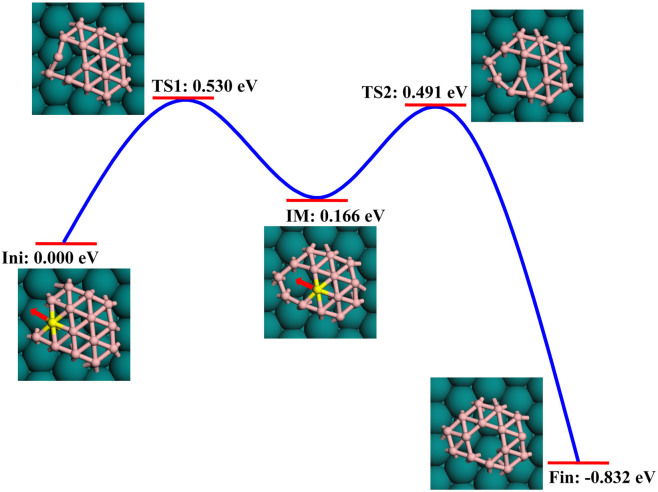
To achieve the patterned ht-BSs (in Figure 1 and Figure S1 of Supporting Information) from continuous growth and coalescence of small boron clusters, creation and redistribution of hexagonal holes are the crucial steps, which can be experimentally realized via proper annealing. To explicitly see how a hexagonal hole arise within a finite triangular network and further diffuse inside a BN cluster, we performed NEB search for the structural transformation from triangular network to hexagonal hole-doped triangular network using B15 as an example. As shown in Figure 6, the initial configuration of B15 is obtained by adding one additional atom to the metastable structure of B14 (14-b) on Cu surface; but this fully triangular network is not favorable for B15. After one atom (highlighted in Figure 6) jumps to the adjacent triangular site, a hexagonal hole occurs as an intermediate (IM) state. The activation barrier for creating of a hexagonal hole as the transition state one (TS1) is 0.531 eV. When a hexagonal hole arises at the edge of a triangular network, it can further diffuse into the cluster interior to be enclosed by as more triangles as possible. As depicted in Figure 6, after the highlighted boron atom migrates from the edge of hexagonal hole to its center with a small activation barrier of 0.491 eV passing through the transition state two (TS2), the energy of Cu-supported B15 cluster is reduced by 0.832 eV. Such small energy barriers for creating and diffusion of a hexagonal hole ensure that a hexagonal hole can arise simultaneously once the triangular network is energetically unfavorable. In principle, the driving force for formation/diffusion of hexagonal holes inside a triangular patch during growth process originates from the formation energy differences ΔEform of various boron sheets, i.e., ΔEform ≥ 0.1 eV/atom between ht-BSs and t-BS, ΔEform = 0.039 eV/atom between g2/15-sheet and struc-1/8-sheet (see Table 1).

Figure 6. Schematic plots for formation and diffusion of a hexagonal hole inside B15 cluster.

Figure 6

Open in a new tab

The energies for the initial (Ini), transition (TS1, TS2), intermediate (IM), and final (Fin) states are given. The migrated atom and its diffusion direction are highlighted.

Discussion

Various types of boron monolayers on Cu(111) surface were investigated using comprehensive ab initio calculations. Most boron monolayers are very stable on Cu(111) surface and retain the same geometries as in vacuum. The formation energies for these boron monolayers are reduced on Cu surface due to metal passivation effect. The final boron sheet synthesised on Cu surface would be the mixture of these ht-BSs due to the small energy differences between these 2D isomers. AIMD simulation at 500 K and 800 K comfirms high thermal stability of the boron sheets on Cu(111) surface.

The lowest-energy and metastable configurations of boron clusters BN (N ≤ 20) on Cu(111) surface were systematically investigated and compared with those in vacuum. On Cu(111) surface, boron atoms tend to form 2D compact clusters on the basis of triangular units and their formation energies continuously reduce with cluster size, which imply the possible incessant growth of 2D boron cluster on Cu substrate. There is a competition between fully triangular structure and mixed triangular and hexagonal structure. Some fragments of ht-BS can be very stable due to metal passivation effect and charge transfer from metal surface to boron clusters, which offer the prerequisite for synthesis of ht-BS. The small diffusion barrier (0.141 eV) also suggests fast migration of boron atoms on Cu surface, which is beneficial for growth of 2D boron patches. NEB search shows that hexagonal holes can easily arise and diffuse in boron cluster during the growth on Cu(111) surface with relatively low energy barriers (about 0.5 eV). Therefore, we proposed two possible ways of boron monolayer growth, i.e., either depositing boron atoms directly on Cu(111) surface or soft landing of small planar BN clusters generated by cluster beam apparatus. Both approaches result in mixed hexagonal-triangular boron sheet on Cu(111) surface after nucleation and thermal annealing. In order to obtain boron monolayer, the evaporation rate of the boron source and the total amount of boron atoms deposited on metal substrate must be strictly controlled. The present theoretical results are undoubtedly very helpful for understanding the atomic structures and growth mechanism of boron monolayer on Cu(111) surface and provide a useful guideline for experiment synthesis of monolayer boron films.

Methods

All calculations were carried out using the Vienna Ab initio Simulation Package (VASP) based on density functional theory (DFT) and planewave basis53. The electron-ion interactions were described by the projector augmented wave (PAW) potentials54. To treat the exchange-correlation interaction of electrons, we chose the Perdew-Burke-Ernzerhof (PBE) functional within the generalized-gradient approximation (GGA)55. A kinetic energy cutoff of 400 eV for the planewave basis and a convergence criterion of 10−4 eV for the total energies were carefully tested and adopted for all DFT calculations.

Here we chose Cu(111) surface as substrate since that it is easy to build co-periodic lattice of boron monolayer and Cu(111) surface and that the boron atom has moderate adhesion energy on Cu surface (about 0.1 eV/Å2)40. Meanwhile, Cu(111) surface is a widely used substrate for epitaxial growth of graphene56,57. The Cu(111) surface was modeled by a three-layer slab model within 2D periodic boundary condition, which was cleaved from fcc Cu solid with an equilibrium lattice constant of 3.63 Å from our first-principles calculations. To avoid interactions between adjacent periodic images, a vacuum space of more than 12 Å was included in the slab model. With fixed supercell parameters, the three-layer slab model was further relaxed with the bottom layer fixed to mimic a semi-infinite solid. The validity of this three-layer slab model was assessed by our test calculations with a five-layer slab model.

Following recent progresses on the 2D boron sheets13,16,17,21,22,23,24, we considered nine possible configurations of boron monolayer on Cu(111) surface. The co-periodic lattices of these boron monolayers and Cu(111) surface were built by compressing or stretching the Cu lattice slightly to fit the 2D unit cell of boron sheet. The small lattice mismatches (Δa and Δb along two crystallographic orientations) between boron sheets and substrates are defined as:

graphic file with name srep03238-m4.jpg
graphic file with name srep03238-m5.jpg

where aSheet, bsheet, asub and bsub are the supercell parameters of the boron sheet and the Cu substrate, respectively. The detailed structural information for these co-periodic lattices of boron sheets and Cu substrate are summarized in Table S1 of the supporting information (Supporting Information). Note that current supercell models of co-periodic lattices are a compromise of computational cost and lattice mismatch. In reality, there should be almost no mismatch if the co-periodic supercell is big enough.

In addition to the infinite boron sheets, BN clusters of different sizes (up to N = 20) were placed on the slab models of Cu(111) surface and the entire cluster-substrate systems were fully relaxed (also with the bottom layer of Cu atoms fixed). The lateral dimensions of the supercell for these cluster-substrate systems were chosen to be sufficiently big to ensure the distance between adjacent clusters no less than 10 Å.

During geometry optimization, the spacing of k point grids was chosen to be 0.03 Å−1 and a convergence criterion of 0.02 eV/Å for force was adopted. In order to obtain more accurate energies and electronic properties, denser k-point meshes with uniform spacing of 0.02 Å−1 were used for calculations of total energy, charge density difference and charge transfer. Bader analysis58,59,60 was preformed to evaluate the charge transfer between Cu(111) surface and boron sheets or clusters.

The strength of interaction between boron monolayer and Cu(111) surface can be characterized by the cohesive energy Ec defined as:

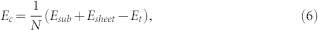graphic file with name srep03238-m6.jpg

where Esub is the energy of substrate, Esheet is the energy of boron monolayer, Et is the total energy of boron monolayer on Cu(111) system, N is the number of boron atoms.

To describe the stability of a boron monolayer or cluster on Cu(111) surface, we define its formation energy as:

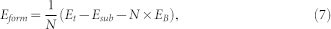graphic file with name srep03238-m7.jpg

where Et and Esub are the same as the definitions in Eq. (6), EB is the energy per atom in the boron solid of α phase44. N is the number of boron atoms in boron monolayer or BN cluster. In a similar manner, we can define the formation energy of boron monolayer or cluster in vacuum (Eformvac) using Eq. (7), where Et becomes the total energy for boron monolayer or cluster only, and the Esub term vanishes.

Author Contributions

H.L., J.G. and J.Z. wrote the main manuscript text. H.L. and J.G. prepared the figures. H.L. did the calculations. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Surpporting Information

srep03238-s1.doc (12.9MB, doc)

Acknowledgments

This work was supported by the National Natural Science Foundation of China (11134005, 11304008), the Program for Changjiang Scholars and Innovative Research Team in University of China, the Fundamental Research Funds for the Central Universities of China (No. DUT12YQ05), the China Postdoctoral Science Foundation (No. 2013M530019) and the Development Fund of China Academy of Engineering Physics (No. 2013B0302056).

References

  1. Novoselov K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004). [DOI] [PubMed] [Google Scholar]
  2. Xu M., Liang T., Shi M. & Chen H. Graphene-like two-dimensional materials. Chem. Rev. 113, 3766–3798 (2013). [DOI] [PubMed] [Google Scholar]
  3. Ivanovskii A. L. Graphene-based and graphene-like materials. Russ. Chem. Rev. 81, 571–605 (2012). [Google Scholar]
  4. Cahangirov S. et al. Two- and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 102, 236804 (2009). [DOI] [PubMed] [Google Scholar]
  5. Ding Y. & Ni J. Electronic structures of silicon nanoribbons. Appl. Phys. Lett. 95, 083115 (2009). [Google Scholar]
  6. Chen L. et al. Evidence for dirac fermions in a honeycomb lattice based on silicon. Phys. Rev. Lett. 109, 056804 (2012). [DOI] [PubMed] [Google Scholar]
  7. Kim K. K. et al. Synthesis of monolayer hexagonal boron nitride on cu foil using chemical vapor deposition. Nano Lett. 12, 161–166 (2011). [DOI] [PubMed] [Google Scholar]
  8. Gonzalez Szwacki N., Sadrzadeh A. & Yakobson B. B80 fullerene: An ab initio prediction of geometry, stability, and electronic structure. Phys. Rev. Lett. 98, 166804 (2007). [DOI] [PubMed] [Google Scholar]
  9. Zhao J., Wang L., Li F. & Chen Z. B80 and other medium-sized boron clusters: Core−shell structures, not hollow cages. J. Phys. Chem. A 114, 9969–9972 (2010). [DOI] [PubMed] [Google Scholar]
  10. Li F. et al. B80 and B101–103 clusters: Remarkable stability of the core-shell structures established by validated density functionals. J. Chem. Phys. 136, 074302 (2012). [DOI] [PubMed] [Google Scholar]
  11. Li H. et al. Icosahedral B12-containing core-shell structures of B80. Chem. Commun. 46, 3878–3880 (2010). [DOI] [PubMed] [Google Scholar]
  12. De S. et al. Energy landscape of fullerene materials: A comparison of boron to boron nitride and carbon. Phys. Rev. Lett. 106, 225502 (2011). [DOI] [PubMed] [Google Scholar]
  13. Tang H. & Ismail-Beigi S. Novel precursors for boron nanotubes: The competition of two-center and three-center bonding in boron sheets. Phys. Rev. Lett. 99, 115501 (2007). [DOI] [PubMed] [Google Scholar]
  14. Tang H. & Ismail-Beigi S. Self-doping in boron sheets from first principles: A route to structural design of metal boride nanostructures. Phys. Rev. B 80, 134113 (2009). [Google Scholar]
  15. Yang X., Ding Y. & Ni J. Ab initio prediction of stable boron sheets and boron nanotubes: Structure, stability, and electronic properties. Phys. Rev. B 77, 041402 (2008). [Google Scholar]
  16. Kunstmann J. & Quandt A. Broad boron sheets and boron nanotubes: An ab initio study of structural, electronic, and mechanical properties. Phys. Rev. B 74, 035413 (2006). [Google Scholar]
  17. Cabria I., Alonso J. A. & López M. J. Buckling in boron sheets and nanotubes. physica status solidi (a) 203, 1105–1110 (2006). [Google Scholar]
  18. Lau K. C., Pati R., Pandey R. & Pineda A. C. First-principles study of the stability and electronic properties of sheets and nanotubes of elemental boron. Chem. Phys. Lett. 418, 549–554 (2006). [Google Scholar]
  19. Lau K. C. & Pandey R. Stability and electronic properties of atomistically-engineered 2D boron sheets. J. Phys. Chem. C 111, 2906–2912 (2007). [Google Scholar]
  20. Galeev T. R. et al. Deciphering the mystery of hexagon holes in an all-boron graphene alpha-sheet. Phys. Chem. Chem. Phys. 13, 11575–11578 (2011). [DOI] [PubMed] [Google Scholar]
  21. Zope R. R. & Baruah T. Snub boron nanostructures: Chiral fullerenes, nanotubes and planar sheet. Chem. Phys. Lett. 501, 193–196 (2011). [Google Scholar]
  22. Penev E. S., Bhowmick S., Sadrzadeh A. & Yakobson B. I. Polymorphism of two-dimensional boron. Nano Lett. 12, 2441–2445 (2012). [DOI] [PubMed] [Google Scholar]
  23. Yu X., Li L., Xu X. & Tang C. Prediction of two-dimensional boron sheets by particle swarm optimization algorithm. J. Phys. Chem. C 116, 20075–20079 (2012). [Google Scholar]
  24. Wu X. et al. Two-dimensional boron monolayer sheets. ACS Nano 6, 7443–7453 (2012). [DOI] [PubMed] [Google Scholar]
  25. Ciuparu D., Klie R. F., Zhu Y. & Pfefferle L. Synthesis of pure boron single-wall nanotubes. J. Phys. Chem. B 108, 3967–3969 (2004). [Google Scholar]
  26. Liu F. et al. Metal-like single crystalline boron nanotubes: Synthesis and in situ study on electric transport and field emission properties. J. Mater. Chem. 20, 2197–2205 (2010). [Google Scholar]
  27. Aufray B. et al. Graphene-like silicon nanoribbons on ag(110): A possible formation of silicene. Appl. Phys. Lett. 96, 183102 (2010). [Google Scholar]
  28. Feng B. et al. Evidence of silicene in honeycomb structures of silicon on Ag(111). Nano Lett. 12, 3507–3511 (2012). [DOI] [PubMed] [Google Scholar]
  29. Vogt P. et al. Silicene: Compelling experimental evidence for graphenelike two-dimensional silicon. Phys. Rev. Lett. 108, 155501 (2012). [DOI] [PubMed] [Google Scholar]
  30. Meng L. et al. Buckled silicene formation on ir(111). Nano Lett. 13, 685–690 (2013). [DOI] [PubMed] [Google Scholar]
  31. Huang W. et al. A concentric planar doubly π-aromatic B19− cluster. Nat. Chem. 2, 202–206 (2010). [DOI] [PubMed] [Google Scholar]
  32. Zhai H. J., Kiran B., Li J. & Wang L. S. Hydrocarbon analogues of boron clusters-planarity, aromaticity and antiaromaticity. Nat. Mater. 2, 827–833 (2003). [DOI] [PubMed] [Google Scholar]
  33. Kiran B. et al. Planar-to-tubular structural transition in boron clusters: B20 as the embryo of single-walled boron nanotubes. Proc. Natl. Acad. Sci. U. S. A. 102, 961–964 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Alexandrova A. N., Boldyrev A. I., Zhai H.-J. & Wang L.-S. All-boron aromatic clusters as potential new inorganic ligands and building blocks in chemistry. Coord. Chem. Rev. 250, 2811–2866 (2006). [Google Scholar]
  35. Romanescu C., Harding D. J., Fielicke A. & Wang L. S. Probing the structures of neutral boron clusters using infrared/vacuum ultraviolet two color ionization: B11, B16, and B17. J. Chem. Phys. 137, 014317 (2012). [DOI] [PubMed] [Google Scholar]
  36. Piazza Z. A. et al. A photoelectron spectroscopy and ab initio study of B21−: Negatively charged boron clusters continue to be planar at 21. J. Chem. Phys. 136, 104310 (2012). [DOI] [PubMed] [Google Scholar]
  37. Sergeeva A. P. et al. B22− and B23−: All-boron analogues of anthracene and phenanthrene. J. Am. Chem. Soc. 134, 18065–18073 (2012). [DOI] [PubMed] [Google Scholar]
  38. Popok V. N., Barke I., Campbell E. E. B. & Meiwes-Broer K.-H. Cluster–surface interaction: From soft landing to implantation. Surf. Sci. Rep. 66, 347–377 (2011). [Google Scholar]
  39. Zhang L. Z. et al. Boron sheet adsorbed on metal surfaces: Structures and electronic properties. J. Phys. Chem. C 116, 18202–18206 (2012). [Google Scholar]
  40. Liu Y., Penev E. S. & Yakobson B. I. Probing the synthesis of two-dimensional boron by first-principles computations. Angew. Chem. 52, 3238–3241 (2013). [DOI] [PubMed] [Google Scholar]
  41. Gao J. & Zhao J. Initial geometries, interaction mechanism and high stability of silicene on ag(111) surface. Sci. Rep. 2, 861 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Andersson S. & Callmer B. The solubilities of copper and manganese in β-rhombohedral boron as determined in CuB~28 and MnB~23 by single-crystal diffractometry. J. Solid State Chem. 10, 219–231 (1974). [Google Scholar]
  43. Bučko T. S., Hafner J. R., Lebègue S. B. & Ángyán J. N. G. Improved description of the structure of molecular and layered crystals: Ab initio dft calculations with van der waals corrections. J. Phys. Chem. A 114, 11814–11824 (2010). [DOI] [PubMed] [Google Scholar]
  44. Donohue J. The structures of the elements. 48 (Wiley, 1974). [Google Scholar]
  45. Chiappe D. et al. Local electronic properties of corrugated silicene phases. Adv. Mater. 24, 5088–5093 (2012). [DOI] [PubMed] [Google Scholar]
  46. Evans M., Joannopoulos J. & Pantelides S. Electronic and mechanical properties of planar and tubular boron structures. Phys. Rev. B 72, 045434 (2005). [Google Scholar]
  47. Gao J. et al. Graphene nucleation on transition metal surface: Structure transformation and role of the metal step edge. J. Am. Chem. Soc. 133, 5009–5015 (2011). [DOI] [PubMed] [Google Scholar]
  48. Gao J. et al. Formation of carbon clusters in the initial stage of chemical vapor deposition graphene growth on Ni(111) surface. J. Phys. Chem. C 115, 17695–17703 (2011). [Google Scholar]
  49. Yuan Q. et al. Magic carbon clusters in the chemical vapor deposition growth of graphene. J. Am. Chem. Soc. 134, 2970–2975 (2011). [DOI] [PubMed] [Google Scholar]
  50. Olsen T., Yan J., Mortensen J. J. & Thygesen K. S. Dispersive and covalent interactions between graphene and metal surfaces from the random phase approximation. Phys. Rev. Lett. 107, 156401 (2011). [DOI] [PubMed] [Google Scholar]
  51. Markov I. V. Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth and Epitaxy. 2nd ed (World Scientific Publishing Co. Pte. Ltd., Singapore, 2003). [Google Scholar]
  52. Lacovig P. et al. Growth of dome-shaped carbon nanoislands on Ir(111): The intermediate between carbidic clusters and quasi-free-standing graphene. Phys. Rev. Lett. 103, 166101 (2009). [DOI] [PubMed] [Google Scholar]
  53. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  54. Kresse G. & Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999). [Google Scholar]
  55. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  56. Gao L., Guest J. R. & Guisinger N. P. Epitaxial graphene on Cu(111). Nano Lett. 10, 3512–3516 (2010). [DOI] [PubMed] [Google Scholar]
  57. Li X. et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 324, 1312–1314 (2009). [DOI] [PubMed] [Google Scholar]
  58. Henkelman G., Arnaldsson A. & Jónsson H. A fast and robust algorithm for bader decomposition of charge density. Comput. Mater. Sci. 36, 354–360 (2006). [Google Scholar]
  59. Sanville E., Kenny S. D., Smith R. & Henkelman G. Improved grid-based algorithm for bader charge allocation. J. Comput. Chem. 28, 899–908 (2007). [DOI] [PubMed] [Google Scholar]
  60. Tang W., Sanville E. & Henkelman G. A grid-based bader analysis algorithm without lattice bias. J. Phys.: Condens. Matter 21, 084204 (2009). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Surpporting Information

srep03238-s1.doc (12.9MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES