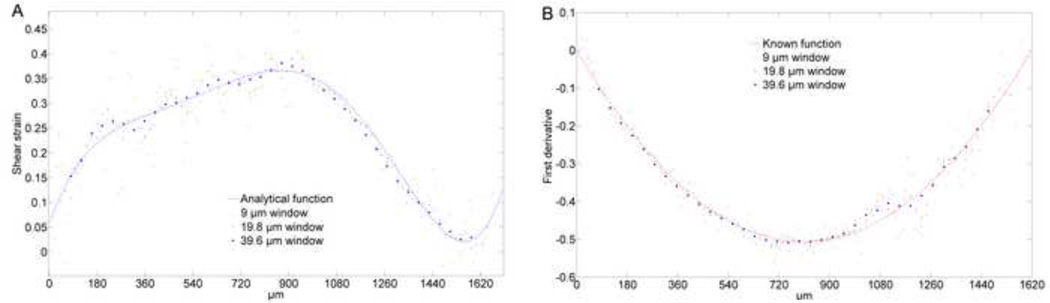
Fig. 11. Comparing first derivatives using analytical and linear numerical methods.
Depth dependent shear strain in native AC computed from the derivative of a 7th order polynomial, and numerical 5PLSQ proceeded by averaging displacements in 9, 19.8, and 39.6 µm windows. As the window size is increased, the numerical derivative becomes smoother and approaches the 7th order polynomial. Note that as the window size is increased, the size of the region near the boundaries where the derivative cannot be computed also increases. The articular surface is on the right side of the plot (A). Known first derivative (slope) of a beam with fixed supports, and numerical 5PLSQ preceded by averaging displacements in 9, 19.8, and 39.6 µm windows. In general, the numerical results are smoother and closer to the known function for the larger window (B).