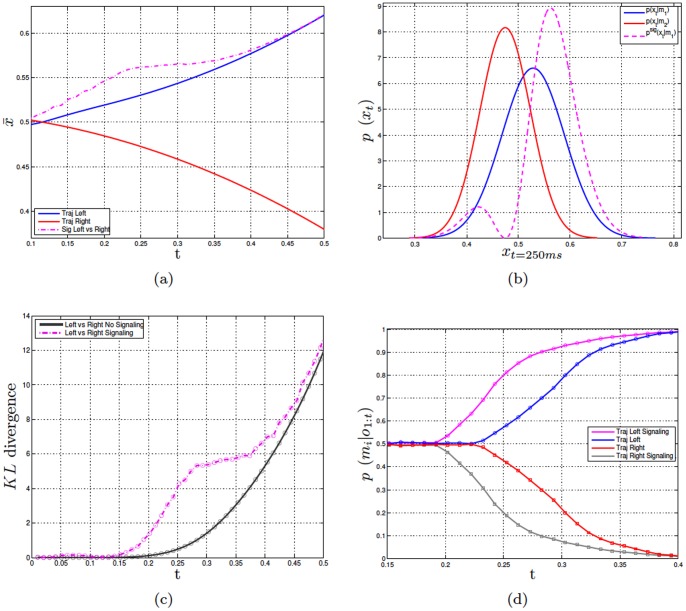
Figure 2. Further analyses of Experiment 1.
Panel a shows the means of the original distributions for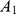 
and 
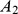in blue and red, respectively. In magenta the means of the signaling distribution of 
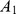(i.e., for a leftward movement) is shown. Panel b shows an example of signaling distribution at a given time step rather than the whole trajectory. Sample distributions 
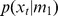and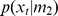 
are taken at time 
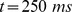of the dynamic Gaussian Process of the two primitives. The parameters of the Gaussian distributions at time 
are 
, 
, 
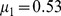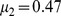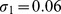and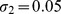 
. The resulting distribution 
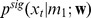is computed from Eq. 
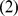. The weights coefficients are set as 
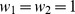. This means that the two distributions are equally weighted in the computing of the signaling distribution. Panel c shows the KL divergence between two actions: 
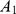vs.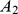 
. Panel d shows the perceiver’s probability of recognizing the right action (i.e., the probability 
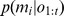of perceiving 
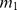given the observations 
until time 
) when the performer uses the original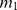 
distribution (blue = left, red = right) and the signaling distribution (magenta = left, black = right).