Abstract
Much of learning disabilities research relies on categorical classification frameworks that use psychometric tests and cut points to identify children with reading or math difficulties. However, there is increasing evidence that the attributes of reading and math learning disabilities are dimensional, representing correlated continua of severity. We discuss issues related to categorical and dimensional approaches to reading and math disabilities, and their comorbid associations, highlighting problems with the use of cut points and correlated assessments. Two simulations are provided in which the correlational structure of a set of cognitive and achievement data are simulated from a single population with no categorical structures. The simulations produce profiles remarkably similar to reported profile differences, suggesting that the patterns are a product of the cut point and the correlational structure of the data. If dimensional approaches better fit the attributes of learning disability, new conceptualizations and better methods to identification and intervention may emerge, especially for comorbid associations of reading and math difficulties.
Keywords: research method, quantitative, classification, reading, math, comorbidity
Since the turn of the past century, when children with unexpected learning and behavioral problems began to be identified, this process of identification has been fraught with problems (Fletcher, Lyon, Fuchs, & Barnes, 2007). Children with learning disabilities (LDs) are heterogeneous and often have more than one type of academic problem (e.g., reading and math difficulties) or share characteristics with another disorder (e.g., attention-deficit/hyperactivity disorder; ADHD). This heterogeneity, along with overlap among potential disorders, has presented formidable difficulties for understanding LDs, both conceptually and empirically.
A Historical Perspective
With the rise of the formal concept of LD and federally led efforts to define them in the 1960s, the third edition of the Diagnostic and Statistical Manual of Mental Disorders (DSM-III; American Psychiatric Association, 1980) formally separated academic skills disorders involving reading, math, and writing from ADHD, which was a set of problems in the behavioral domain involving inattention, hyperactivity, and impulsivity. With classifications like the DSM-III, it was recognized that a child could have problems with reading, math, and/or ADHD. These patterns are now recognized as comorbid associations that share common genetic factors as well as disorder-specific factors (Plomin & Kovas, 2005; Willcutt, Betjemann, et al., 2010; Willcutt, Pennington, et al., 2010).
The recognition of comorbidity, however, has not helped to identify individuals who share attributes that make them members of these hypothetical classes of disorders. The initial regulatory definition of LD (U.S. Office of Education, 1977) used a discrepancy between aptitude (usually a score on an IQ test) and achievement test score as a formal operationalization of the definition of LD. This approach was supported by the Isle of Wight studies (Rutter & Yule, 1975), which showed a qualitative break in the distribution of reading scores suggesting a distinction between children with reading achievement well below IQ (“specific reading retardation”) and reading consistent with IQ (“generally poor reading”). This finding was important because it implied that children with the two forms of reading difficulties had demarcated differences in reading and other characteristics and that a boundary could be identified that differentiated the two groups.
At the time it was not appreciated that the Isle of Wight study was epidemiological and included children with brain injury and intellectual disabilities: The average IQ of the generally poor readers was about 70 (Fletcher et al., 1998). The qualitative break in the distribution was the result of the inclusion of children with low IQ scores. Subsequent epidemiological studies around the world have largely failed to show qualitative breaks in the distribution of either reading scores (Rodgers, 1983; Shaywitz, Escobar, Shaywitz, Fletcher, & Makuch, 1992; Silva, McGee, & Williams, 1985) or math scores (Lewis, Hitch, & Walker, 1994; Shalev, Auerbach, Manor, & Gross-Tsur, 2000). Large-scale behavior genetic studies have also been more consistent with continuous distributions (Plomin & Kovas, 2005), supporting a dimensional view of the achievement attributes of reading disability (i.e., a continuum of severity with no natural breaks that would identify groups).
Snowling and Hulme (2012) argued for a dimensional conceptualization of problems with reading decoding and reading comprehension, echoing earlier arguments by Ellis (1984). Snowling and Hulme argued that there was comorbidity between forms of reading difficulties and other forms of language impairment as a set of correlated dimensions. We can also ask whether reading and math are correlated dimensions with no real group structure. In fact, we have two opposing hypotheses. The first, single-population hypothesis posits that children with LD in reading and/or math are drawn from a single population of continuous abilities that are related. The opposing hypothesis suggests that children with reading and/or math LD are drawn from at least two distinct populations. In the case of comorbid associations between reading and math LD, are there two qualitatively distinct categories of reading and math LD that sometimes co-occur, or are there two correlated dimensions where some people are simply low on both?
Beyond the multiple applications of methods such as cluster analysis to cognitive data exploring possible subtypes in LD samples (see Fletcher et al., 2007, for a review), there has been little examination of the issue of categorical versus dimensional approaches in the LD area using classification methods. The search for subtypes using exploratory methods like cluster analysis (or even a priori definitions of subgroups) has not been satisfactory or sustaining because reliable subtypes could be created, but relations with external variables (especially treatment) were weak. Close examination of profiles in large cluster analysis studies seems to reflect cuts of a continuous distribution as opposed to qualitatively different subgroups (Morris et al., 1998).
In fact, there is a wide variety of models that might represent comorbid associations (Neale & Kendler, 1995; Rhee, Hewitt, Corley, Willcutt, & Pennington, 2005). Even if the attributes are dimensional, it is possible to have different degrees of correlation that will result in different numbers in the comorbid group. If the two distributions (e.g., reading and math achievement) are uncorrelated, the proportion in the comorbid group will be smaller: If 10% are math disabled (MD) and 10% are reading disabled (RD), then only 1% will be expected to be both RD and MD. However, almost all models rely on the use of cut points on the achievement distributions and have not always considered the potential problems created by cut points on dimensions.
Psychometric Issues With Cut Points
Researchers usually define children with reading and math disabilities by introducing a threshold (i.e., cut point) on the distribution of reading and/or math achievement. Children have potentially comorbid disorders if they are below the threshold on both distributions. A common approach has been to compare children with only reading, only math, and both reading and math difficulties on a set of cognitive variables not used to define the groups (Fletcher, 1985; Rourke & Finlayson, 1978; Willcutt, Betjemann, et al., 2010). The groups generally differ in the shape of their cognitive skill profiles, with the group with both reading and math problems having more severe academic and cognitive problems, but still showing similarities with the reading and math difficulty groups.
It is well known that cognitive discrepancies based on differences in aptitude and achievement measures do not have strong validity based on two meta-analyses of the literature (Hoskyn & Swanson, 2000; Stuebing et al., 2002). Similarly, other approaches to defining cognitive discrepancies as a pattern of strengths and weaknesses across cognitive tests have been found to have poor reliability (Kramer, Henning-Stout, Ullman, & Schellenberg, 1987; Macmann, Barnett, Lombard, Belton-Kocher, & Sharpe, 1989; Stuebing, Fletcher, Branum-Martin, & Francis, 2012). Other approaches that use instructional response as part of the identification criteria for LD show similar unreliability (Barth et al., 2008). In the math area, it has been proposed that children who perform below the 10th percentile have a specific LD and those between the 10th and 25th percentiles are low achieving (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007), but the reliability of these within-group distinctions has not been evaluated. What is less frequently recognized is that virtually any approach that involves creating a cut point on a single indicator, whether it is an assessment of achievement, IQ, cognitive functions, or instructional response, is unreliable in identifying individual children as LD or not LD in real and simulated data (Francis et al., 2005; Macmann & Barnett, 1985), partly because there is always measurement error.
Even small amounts of measurement error lead to unreliability in detection of specific individuals as a member of a category (Cohen, 1983). This problem has major implications for the identification of individual children because their eligibility for services depends on their classification into a category of LD.
Cut scores have less effect on research because individuals around the cut point are usually very similar, but power is reduced because of the adoption of a categorical approach and the subdivision of a continuous distribution. Markon, Chmielewski, and Miller (2011) synthesized 58 studies addressing the reliability and validity of dimensional versus categorical approaches to the measurement of psychopathology. With dimensional classifications, reliability was 15% higher and validity was 37% higher than with a categorical approach. For research, this translates to more precision of measurement and an increase in power that would be especially beneficial to small studies. Dichotomization of continuous variables is well established to reduce reliability and power (see review by MacCallum, Zhang, Preacher, & Rucker, 2002).
Research Question
These observations are not designed to dispute the existence of comorbidity, where both real data and simulations provide strong support for the notion (Neale & Kendler, 1995; Rhee et al., 2005; Willcutt, Pennington, et al., 2010). The question we address is how to conceptualize comorbidity if there were no true groups in the data, and the attributes represented dimensions. It is a common practice in LD research to define groups as “LD” versus “typical” based on a cut score on one or more continuous scores which are correlated. Subsequently, mean differences (in the form of profile plots, regressions, or ANOVAs) are examined on other academic and cognitive outcomes (which are also correlated with the initial tests). These analyses are often interpreted (at least implicitly) as if they support the central idea that LD groups are qualitatively different. This approach is especially common in studies of comorbidity. We illustrate with simulations and graphical results how using cut scores without specific analytic restrictions can seem to produce group differences from homogeneous data without groups.
The present article simulates data based on two research studies, one from education (Fletcher et al., 2011) and the other from behavioral genetics (Willcutt, Betjemann, et al., 2010). We simulate data, replicating the correlational structure found in these two studies, but with no group structure. Our intention is to illustrate the conceptual and statistical dangers in using cut scores without a specific method designed to account for the correlation among the measures. Our motivating research question is this: What is the extent to which cut scores on correlated outcomes produce groups which appear qualitatively different, even though the data were specifically created with no group structure (i.e., are the created groups simply an artifact of cut scores)? If simulated data from two sets of typical academic correlations show that cut scores on correlated dimensions produce differential profiles of mean differences that reflect the cut scores and differential correlations, then findings from these types of studies may not reflect qualitative differences in the populations.
Study 1
Method
Participants
The 258 children in Fletcher et al. (2011) were assembled to evaluate the efficacy of a Grade 1 Tier 2 reading intervention (Denton et al., 2011). The students included 69 typically developing children and 189 children at risk for reading problems at the beginning of Grade 1 who were randomized to three reading interventions. After the intervention, there were 85 children who met criteria indicating adequate response to intervention and 104 who showed an inadequate response to intervention based on different benchmarks for successful outcomes. These children received a battery of cognitive and academic tests at the end of the reading intervention. Fletcher et al. (2011) focused on differences in adequate and inadequate responders, reporting only quantitative differences in the level of functioning. In this example, we use the data to simulate profiles of cognitive tests and associations of reading and math disability in a sample with no group structure.
Measures
The measures used in this study were described in Fletcher et al. (2011) and were originally selected to measure different reading and math skills, and their established cognitive correlates. For this simulation, we selected verbal and nonverbal measures that represented outcomes common in LD research and that varied in reliability because these differences may influence the appearance of groups and profiles. The measures included well-known measures from the Woodcock–Johnson III Test of Achievement (Woodcock, McGrew, & Mather, 2001): reading decoding (Basic Reading composite), reading comprehension (Passage Comprehension), and math computations (Calculations). Math achievement involving word problems was assessed with the Single Digit Story Problems, a 14-item word problems test used frequently across Grades 1 to 3 to assess student performance on simple word problems (Jordan & Hanich, 2000). The Phoneme Awareness composite and Rapid Letter Naming tests were used from the Comprehensive Test of Phonological Processing (Wagner, Torgesen, & Rashotte, 1999). A measure of spatial working memory from Cirino (2002) was used. Finally, the Verbal Knowledge (vocabulary and lexical skills) and Nonverbal Reasoning (matrices) subtests were used from the Kaufman Brief Intelligence Test–2 (Kaufman & Kaufman, 2004).
Analysis
The analysis was carried out in three steps. The correlation matrix of the nine measures listed above (Table 1) was inputted into macro “corr2data.sas” from the UCLA Academic Technology Services, Statistical Consulting Group (http://www.ats.ucla.edu/stat/sas/macros/corr2data_demo.htm), and 10,000 observations were generated from a multivariate normal distribution (i.e., it had no inherent group structure). The resulting data matched the target correlational structure.
Table 1.
Correlation Matrix Used for Generating the Data (Fletcher et al., 2011)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 1. Basic Reading | 1.00 | ||||||||
| 2. Calculation | .63 | 1.00 | |||||||
| 3. Passage Comprehension | .87 | .57 | 1.00 | ||||||
| 4. Phonological Awareness | .71 | .49 | .71 | 1.00 | |||||
| 5. Matrix | .42 | .36 | .48 | .44 | 1.00 | ||||
| 6. Verbal Knowledge | .38 | .31 | .46 | .49 | .31 | 1.00 | |||
| 7. Rapid Letter | .30 | .16 | .33 | .23 | .05 | .26 | 1.00 | ||
| 8. Digit Story | .35 | .42 | .41 | .38 | .35 | .35 | .05 | 1.00 | |
| 9. Spatial | .08 | .16 | .13 | .16 | .12 | .10 | −.01 | .19 | 1.00 |
Note: All variables are z scores. The shaded columns show the measures on which a cut was made to determine group membership for low performance in reading and math.
Second, groups of “LD” children were created by cutting the distributions of Basic Reading and Calculations. The group with reading disabilities was defined as any score on Basic Reading 1.25 standard deviations below the population mean. Similarly, the group with MD was defined as 1.25 standard deviations below the population mean on the Calculation test. Scores below −1.25 standard deviations on both measures represent the potentially comorbid group (RD + MD). In this way, four groups were formed. Note that in a normal distribution, we would expect to find 10.6% of the observations to fall below a cut point of z = −1.25, which is consistent with the marginal percentages found in Table 2. In addition, we see that the groups formed from the 10,000 examinees represented 5.0% to 6.2% in each of the three LD groups. A total of 17% of students had some form of low performance that placed then into a “disability” group. The expected percentage in the comorbid group would have been approximately 1% if reading and math were uncorrelated. The observed 6.2% in this cell is consistent with the simulated, strongly positive correlation (r = .63 between reading and math).
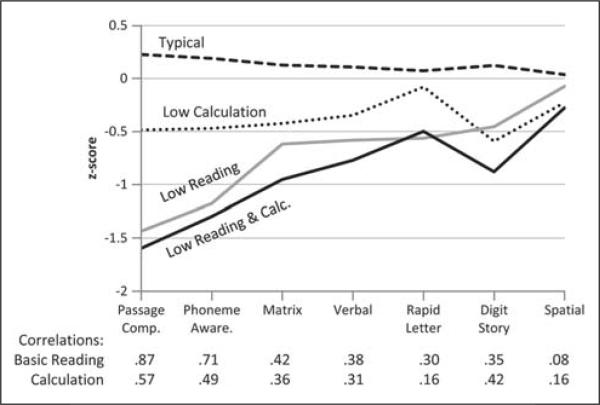
Third, the profiles of means for each of these fabricated groups were graphed for the seven remaining measures (Passage Comprehension, Phoneme Awareness, Matrix, Verbal Knowledge, Rapid Letter Naming, Single Digit Story Problems, and Spatial Working Memory; see Figure 1). Error bars are not shown because this information would only reflect the arbitrary precision based on the size of the simulated sample (we could make them as small as desired by simulating more students).
Figure 1.
Profile plot of groups from simulated data (after Fletcher et al., 2011).
Results
Figure 1 shows the means for each of the four groups: typical, RD, MD, and RD + MD. At the top of the graph, the dashed line shows the profile of means for the typical group. The means for the typical group stand slightly above zero (population mean) because we have removed students who performed 1.25 standard deviations below the mean to form the other groups. The MD-only group is shown as a dotted line that goes through the middle of the graph. The RD group and RD + MD group (solid gray and black, respectively) follow each other closely at the bottom of the graph, with low performance on the leftmost measures and performance approaching the typical group on the measures more to the right of the graph. The correlations of each profile variable with the grouping variables (Basic Reading and Calculations) are included with this plot as an aid in interpretation. In this sample, Passage Comprehension is highly correlated with Basic Reading (r = .87). As a result, the groups are well separated on this variable. Variables with the highest correlations with Basic Reading show ordering of means consistent with this pattern, although the separation is less marked as the correlation declines. By contrast, Spatial Working Memory (SWM), which is lower in reliability than other measures, has low correlations with both grouping variables. As a result, the means of all four groups cluster tightly, indicating that the variability in SWM is primarily within groups instead of between groups. However, because this variable is more strongly related to Calculations than to Basic Reading, the groups are reordered relative to most of the verbally loaded variables, with the typical and RD groups outperforming the MD and RD + MD groups. Single Digit Story Problems has moderate correlations with both grouping variables, separating all of the impaired groups from the typical group.
The resulting set of profiles suggests a group by measure interaction where the differences between groups are different across the seven measures. Historically, this pattern has been interpreted as evidence that the groups are qualitatively different (Fletcher, 1985; Rourke & Finlayson, 1978; Willcutt, Betjemann, et al., 2010) when in fact all observations in this simulation have come from a single homogeneous population. The shape differences among the profiles are entirely the result of differential correlations of the profile variables with the variables used to form groups. The strength of the correlation affects the degree of separation of the group means and the pattern of correlations of the profile variables with the grouping variables affects the ordering of the group means, potentially producing patterns of crossing profile lines and suggesting qualitative group differences.
Study 2
Method
Participants
Willcutt, Betjemann, et al. (2010) compared cognitive profiles in groups of children identified with only reading decoding problems, only ADHD, both RD and ADHD, and typically developing children. The sample involved 487 twin pairs evaluated using an extensive battery of cognitive tests as part of the Colorado Family Reading Study. A cutoff of z = −1.25 on the word reading was used to select students as RD and clinical criteria were used to select ADHD students. Using multiple methods, the authors concluded that both RD and ADHD stemmed from multiple cognitive deficits and that a deficit in processing speed was common to both. They did not separately compare RD and ADHD groups to a comorbid group, but produced profiles of the four groups on the six variables (see their Figure 2, p. 1353). Willcutt, Betjemann, et al. (2010) explicitly acknowledged issues related to categorical versus dimensional assumptions and completed both types of analyses to support their conclusions of common and disorder-specific associations. We selected the study because of the group profiles and to explore comorbidity in disorders where the defining attributes may be less highly correlated than in studies of RD and MD.
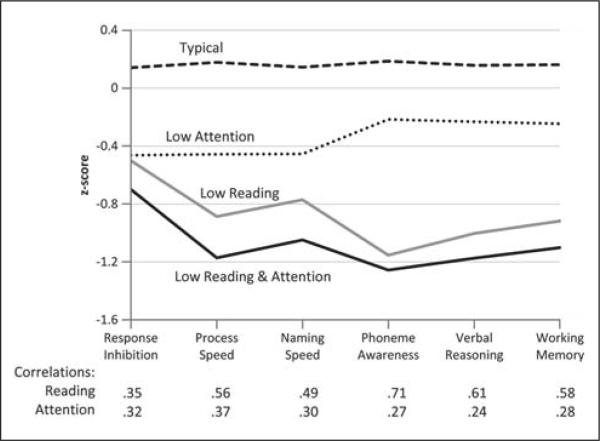
Figure 2.
Profiles on correlated measures for groups created for reading and attention performance (after Willcutt, Betjemann, et al., 2010).
Measures
Each measure used was a latent variable estimate from 2 to 5 high-quality tests and clinical reports. These latent variable estimates represent factor scores that control for the measurement error in the separate tests that composed them (see Willcutt, Betjemann, et al., 2010). These factor scores with the number of measures used to derive each score were Single Word Reading (3), Attention (2), Phoneme Awareness (3), Verbal Reasoning (4), Working Memory (4), Response Inhibition (2), Processing Speed (5), and Naming Speed (5). Each of the individual measures used had reasonable to high reliability, so the latent composites are even more reliable estimates of the common variability for each factor.
Analysis
The analysis of Study 2 followed the same three steps as Study 1: First, we generated 10,000 examinees from the correlation matrix (Table 3) provided in Willcutt, Betjemann, et al. (2010) and verified that the resulting data reproduced the target correlations. Note that the correlation between word reading and attention was r = .35, substantially lower than the correlation between grouping variables in Study 1 (r = .63, between reading and math).
Table 2.
Group Membership for 10,000 Generated Examinees
| Group | Low Math (%) |
Typical Math (%) |
Total (%) |
|---|---|---|---|
| Typical reading | 5.9 | 83.4 | 89.3 |
| Low reading | 6.2 | 4.5 | 10.7 |
| Total | 10.4 | 89.6 | 100.0 |
Note: Totals may be affected by rounding. Low-performing groups were each defined by < −1.25 SD on the respective Basic Reading and Calculation measures.
Second, we cut the distributions of word reading and attention at z = −1.25 to form groups that were impaired in reading alone (RD), in attention alone (Low Attention), both (RD + Low Attention), or neither (Typical). The Hyperactivity–Impulsivity dimension was ignored in this simulation. Table 4 shows the percentages of students in each group. The observed percentage of comorbid observations is 2.6%, whereas the expected value with no correlation between grouping variables would have been 1% or the same as in Study 1 because the marginal frequencies were the same in both studies. We are not surprised to find a smaller percentage of comorbid observations because of the lower correlation between grouping variables in this study.
Table 4.
Group Membership for 10,000 Generated Examinees
| Group | Low Attention (%) |
Typical Attention (%) |
Total (%) |
|---|---|---|---|
| Typical reading | 8.1 | 81.5 | 89.6 |
| Low reading | 2.6 | 7.8 | 10.4 |
| Total | 10.7 | 89.3 | 100.0 |
Note: Totals may be affected by rounding. Low-performing groups were each defined by < −1.25 SD on the respective Word Reading and Attention measures.
Finally, the means of the six factors (Response Inhibition, Processing Speed, Naming Speed, Phoneme Awareness, Verbal Reasoning, and Working Memory) were plotted for each of the four groups (Figure 2). The order of the variables was the same as in Figure 2 of Willcutt, Betjemann, et al. (2010) to facilitate comparisons between what was produced by an empirical sample and what was generated on the basis of correlations and the assumption of multivariate normality within a single population.
Results
The profile plot in Figure 2 reproduces quite closely the patterns of group means found in the original article (Willcutt, Betjemann, et al., 2010, p. 1353, Figure 2). The bottom of Figure 2 shows the correlations of the word reading and attention scores with the respective grouping variables. The distances between the groups correspond to the respective correlations quite closely in that larger correlations show larger disparities between the groups. Because most of the variables are moderately or highly correlated with Reading and to a lesser degree with Attention, the two problem reading groups (RD and RD + Attention) cluster together and tend to be separate from the two groups without reading problems, which also cluster together. Response Inhibition differs from this pattern in that the two correlations are moderate and of approximately equal size with the result that all of the impaired groups are separated from the Typicals on this variable. No variable is more strongly correlated to Attention than to Reading, and as a result there are no crossing profiles as we observed in Study 1, Figure 1. Finally, note that the visual appearance of the mean differences is a result of the chosen display order of the outcomes with respect to the reading variable (i.e., the profiles could seem to “converge” if we reversed the order of the outcomes because the correlations with the reading variable follow this pattern).
Discussion
The data for these two studies were correlation matrices from two studies of reading, math, and ADHD comorbidity, covering reading, math, cognitive, and behavioral outcomes. The data we generated contained no natural groups. From this homogeneous population, we artificially created groups solely on the basis of low performance on two measures. In both studies, profile plots had the appearance of being substantively different. If the data had not been simulated, the temptation would be to interpret the differences in profiles to reflect qualitatively distinct subpopulations. Instead, the profiles simply reflect slices from a single population on multiple correlated measures. Note that Fletcher et al. (2011) did not evaluate comorbidity but concluded that the comparisons of adequate and inadequate responders represented a continuum of severity. Willcutt, Betjemann, et al. (2010) did not formally evaluate the profiles we simulated and used a variety of approaches to suggest common and more distinct associations of cognitive functions, reading disability, and ADHD. They acknowledged that their data could be interpreted from a dimensional perspective.
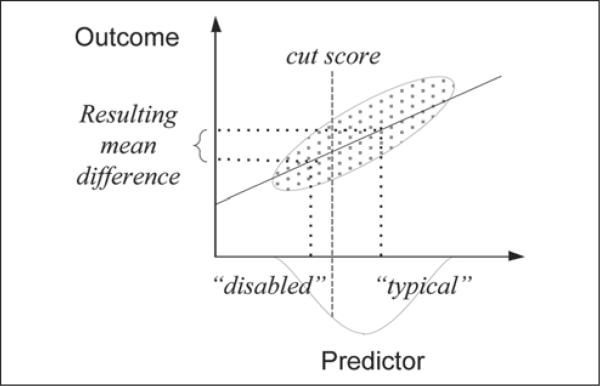
Standard statistical models in true group designs, where participants are randomized into groups, contain an expectation that the groups will not be different from each other on some outcome except for treatment effects and sampling error. When groups are formed by taking segments of a distribution of scores, the expected difference between them depends on the correlation between the outcome variable and the variable being dichotomized. Figure 3 presents a conceptual illustration of how cut scores produce differences on correlated measures. The horizontal axis represents a test score, a “predictor,” used to define groups by a cut score (e.g., Basic Reading or math performance). The cut score is represented by a vertical dashed line. The vertical axis represents another, correlated outcome such as an achievement or cognitive measure. The diagonal ellipse shows the bivariate scatter of student test scores for the correlated predictor and outcome. The diagonal solid line represents the linear regression of the outcome on the predictor. After cutting the predictor, the estimated means for the lowperforming and typical-performing groups are shown as dotted lines dropping vertically to the cut predictor. Because the predictor is linearly related to the outcome, the dotted lines show an expected mean difference between the low and typical groups on the vertical axis also. This mean difference is the appropriate null value when comparing these groups.
Figure 3.
Illustration of the effect of a cut score on a correlated outcome.
When cuts are made on two predictors such as reading and math, and their correlations with a third outcome are different, the relative sizes of the mean differences on the outcomes will vary. This is likely to produce diverging and even crossing lines in a profile plot of the means. The sizes of these expected differences are also likely to create differential patterns of mean differences in predictors in a regression, ANOVA, or even a cluster analysis. These patterns can be seen in Figures 1 and 2, where the correlations of the two predictors are shown for each outcome below the horizontal axis.
A major implication of these results is that regression and ANOVA models following such group selection procedures may be statistically circular. Regression and ANOVA models with nil null hypotheses (i.e., assuming zero differences; Cohen, 1994) are usually exploratory and ignore the fact that the vast majority of educational and cognitive measures are positively correlated (see Lykken, 1968; Meehl, 1986).
Another approach beyond contrasting groups is to examine longitudinal models, especially those tested with groups randomized to alternative treatments designed to affect different possible learning deficits or mechanisms. Such differential effectiveness studies can shed light not only on what works, but also on the causal nature of underlying problem(s)—to the extent that the problem is more than simply low performance. However, when fitting growth models, it could be important to recognize that the slopes represent additional correlated variables either to be cut or to receive group differences from cut scores. Also, most growth modeling approaches allow for continuous variability, which makes subgrouping unnecessary and sometimes poorly motivated (Bauer, 2007; Raudenbush, 2005).
As another alternative, direct investigation of issues concerning dimensional versus categorical classifications would be helpful. In addition to cluster analysis, methods for identifying taxa (classes) emerged in the work of Meehl (1992) and are known as “taxometric methods.” In Meehl’s formulation, taxa are latent structures that exist independently of our ability to measure them. They can be operationalized and measured, but efforts at measurement will be imperfect, so convergence across methods is often sought. If a taxon exists, its boundary can be empirically detected (Ruscio, Haslam, & Ruscio, 2006). Members of the taxon are qualitatively different from members outside the taxon. Taxometric methods attempt to identify taxons and test hypotheses about whether there are classes within a distribution.
Many of these taxometric procedures can be seen as simplifications of general linear and nonlinear factor analytic approaches (McDonald, 2003). This more general latent variable approach is embodied in factor mixture models in which factor models for continuous latent traits (e.g., severity) are combined with latent class models to detect unobserved groups of individuals as subtypes or qualitatively different subpopulations (see review by Lubke & Muthén, 2005). The resulting models can simultaneously detect classes of individuals who might also differ in severity on a continuous factor. For example, Lubke et al. (2007) applied latent class models, factor models, and factor mixture models to ratings of inattention and hyperactivity–impulsivity from an epidemiological cohort of more than 16,000 Finnish teenagers. They found that within both males and females, a model with two classes, each of which differed on two continuous factors representing the severity of inattention and hyperactivity–impulsivity, provided the best fit. Further inspection of the profiles of the latent classes, however, demonstrated that the minority group differed from the majority only in severity. That is, there was no evidence of separate inattentive, hyperactive–impulsive groups (Lubke et al., 2007).
Factor mixture models offer the opportunity to test qualitatively distinct groups which may have biologically based differences expressed in the measurement relations among tests and items. Application of these methods can be done with existing data, provided they are large, epidemiological samples and are not necessarily smoothed to reduce the likelihood of qualitative breaks in the distributions. This study simulated data from the correlation matrices of just two studies. However, the message of the demonstration does not lie in the samples chosen or in the profile variables selected but in the logic of the underlying relations among groups formed by dichotomizing continua and variables correlated with those continua.
It is likely that much of the taxometric approach (Waller & Meehl, 1998) can be subsumed under general latent variable models (McDonald, 2003) or under covariance modeling reflecting specific causal hypotheses (Neale & Kendler, 1995; Rhee et al., 2005). These approaches, however, require very large samples and may not be appropriate where participants are selected to represent extreme groups (unless design-based sampling weights are used).
Conclusions
None of the methods we have recommended as alternatives to the profile approach are without flaws. This study simulated data from the correlation matrices of just two studies. However, the message of the demonstration does not lie in the samples chosen or in the profile variables selected but in the logic of the underlying relations among groups formed by dichotomizing continua and variables correlated with those continua.
The current findings and observations do not suggest that disabilities do not exist, nor do they imply that disabilities are not measurable. Whether the attributes of LD derive from a single population or represent discrete groups is still an empirical question that requires systematic examination. The issue is whether it makes sense to treat LDs in reading and math as categories. Indeed, approaches to MD that simply subdivide the distribution of math scores based on severity may well lead to profile differences of the sort we created through simulation. Simply put, cutting groups of students by high and low performance often results in circular analyses that do not reveal much about the functional nature of disability.
Instead of an exploratory null model, theory and prior findings could be used to frame a testable model. Usually, such models impose restrictions on the possible patterns of data beyond simply mean differences (Neale & Kendler, 1995). As in the present study, expected relations could be simulated and compared with empirical results to understand deviations from expectations. In the RD area, Stanovich and Siegel (1994) used regression to control for reading level and test for the improvement in prediction of classification group, implicitly using a nonzero null for the IQ-discrepant versus low achievement classification hypothesis, failing to find evidence supporting this distinction. Behavioral genetic data also offer the opportunity to test alternative theories of genetic versus environmental influence.
Where these issues are especially important is the common practice of identifying individual people as LD in reading and/or math or with ADHD based on cut score approaches. If dimensional assumptions prevail, this approach is questionable, especially if the thresholds represent single indicators. Obesity is an excellent example of a problem that is dimensional, but potentially very disabling. Although weight is certainly the defining attribute, obesity is usually evaluated using multiple indicators relating to different risk indicators, including other diseases, reductions in independence, and death. The main focus is not on a single cut point applied to all people, but on the need for intervention. Likewise in LD, poor performance in reading and/or math is a basis for intervention, but there is a need to evaluate the role of categorical classifications and rigid cut points as triggers for these interventions.
As Fuchs and Fuchs (1998; Fuchs et al., IN PRESS [this issue]) have suggested, focusing on treatment and intervention response may provide an alternative to the overriding emphasis on categorical diagnosis so characteristic of the LD area. In addition, identifying someone with a disability is at least a two-pronged decision: evidence of a disorder and that the disorder has functional or educational consequences. Identifying a person as LD cannot be simplified to an unreliable threshold on a single indicator. Similarly, identifying comorbidity because of poor performance on two correlated indicators is increasingly hard to justify.
Table 3.
Correlation Matrix of Cognitive Factor Scores from Willcutt, Betjemann, et al. (2010)
| Measure | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1. Word Reading | 1.00 | |||||||
| 2. Attention | .35 | 1.00 | ||||||
| 3. Response Inhibition | .35 | .32 | 1.00 | |||||
| 4. Processing Speed | .56 | .37 | .34 | 1.00 | ||||
| 5. Naming speed | .49 | .30 | .30 | .59 | 1.00 | |||
| 6. Phoneme Awareness | .71 | .27 | .38 | .46 | .45 | 1.00 | ||
| 7. Verbal Reasoning | .61 | .24 | .32 | .47 | .34 | .53 | 1.00 | |
| 8. Working Memory | .58 | .28 | .33 | .43 | .42 | .64 | .49 | 1.00 |
Note: All variables are z scores. The shaded columns and rows show the measures on which a cut was made to determine group membership (Willcutt, Betjemann, et al., 2010, p. 1352, Table 2).
Acknowledgments
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This research was supported in part by Grant P50D052117, Texas Center for Learning Disabilities, from the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NICHD or the National Institutes of Health.
Footnotes
Declaration of Conflicting Interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- American Psychiatric Association . Diagnostic and statistical manual of mental disorders. 3rd Author; New York, NY: 1980. [Google Scholar]
- Barth AE, Stuebing KK, Anthony JL, Denton CA, Mathes PG, Fletcher JM, Francis DJ. Agreement among response to intervention criteria for identifying responder status. Learning and Individual Differences. 2008;18:296–307. doi: 10.1016/j.lindif.2008.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer DJ. Observations on the use of growth mixture models in psychological research. Multivariate Behavioral Research. 2007;42(4):757–786. [Google Scholar]
- Cirino PT. Relation of working memory and inhibition to executive function and academic skill. Journal of the International Neuropsychological Society. 2002;8(2):230. [Google Scholar]
- Cohen J. The cost of dichotomization. Applied Psychological Measurement. 1983;7:249–253. [Google Scholar]
- Cohen J. The Earth is round (p < .05) American Psychologist. 1994;49(12):997–1003. [Google Scholar]
- Denton CA, Cirino PT, Barth AE, Romain M, Vaughn S, Wexler J, Fletcher JM. An experimental study of scheduling and duration of “Tier 2” first grade reading intervention. Journal of Research on Educational Effectiveness. 2011;4(3):208–230. doi: 10.1080/19345747.2010.530127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis AW. The cognitive neuropsychology of developmental (and acquired) dyslexia: A critical survey. Cognitive Neuropsychology. 1984;2:169–205. [Google Scholar]
- Fletcher JM. Memory for verbal and nonverbal stimuli in learning disability subgroups: Analysis by selective reminding. Journal of Experimental Child Psychology. 1985;40:244–259. doi: 10.1016/0022-0965(85)90088-8. [DOI] [PubMed] [Google Scholar]
- Fletcher JM, Francis DJ, Shaywitz SE, Lyon GR, Foorman BR, Stuebing KK, Shaywitz BA. Intelligent testing and the discrepancy model for children with learning disabilities. Learning Disabilities Research & Practice. 1998;13:186–203. [Google Scholar]
- Fletcher JM, Lyon GR, Fuchs LS, Barnes MA. Learning disabilities: From identification to intervention. Guilford; New York, NY: 2007. [Google Scholar]
- Fletcher JM, Stuebing KK, Barth AE, Denton CA, Cirino PT, Francis DJ, Vaughn S. Cognitive correlates of inadequate response to intervention. School Psychology Review. 2011;40:2–22. [PMC free article] [PubMed] [Google Scholar]
- Francis DJ, Fletcher JM, Stuebing KK, Lyon GR, Shaywitz BA, Shaywitz SE. Psychometric approaches to the identification of LD: IQ and achievement scores are not sufficient. Journal of Learning Disabilities. 2005;38(2):98–108. doi: 10.1177/00222194050380020101. [DOI] [PubMed] [Google Scholar]
- Fuchs LS, Fuchs D. Treatment validity: A unifying concept for reconceptualizing the identification of learning disabilities. Learning Disabilities Research & Practice. 1998;13(4):204–219. [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development. 2007;78(4):1343–1359. doi: 10.1111/j.1467-8624.2007.01069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoskyn M, Swanson HL. Cognitive processing of low achievers and children with reading disabilities: A selective meta-analytic review of the published literature. School Psychology Review. 2000;29:102–119. [Google Scholar]
- Individuals with Disabilities Education Improvement Act. 2004. Pub. L. No. 108-446, 118 Stat. 2647.
- Jordan NC, Hanich LB. Mathematical thinking in second-grade children with different forms of LD. Journal of Learning Disabilities. 2000;33:567–578. doi: 10.1177/002221940003300605. [DOI] [PubMed] [Google Scholar]
- Kaufman AS, Kaufman NL. Kaufman Brief Intelligence Test. 2nd Pearson; Minneapolis, MN: 2004. [Google Scholar]
- Kramer JJ, Henning-Stout M, Ullman DP, Schellenberg RP. The viability of scatter analysis on the WISC-R and the SBIS: Examining a vestige. Journal of Psychoeducational Assessment. 1987;5:37–47. [Google Scholar]
- Lewis C, Hitch GJ, Walker P. The prevalence of specific arithmetic difficulties and specific reading difficulties in 9- to 10-year-old boys and girls. Journal of Child Psychology and Psychiatry. 1994;35:283–292. doi: 10.1111/j.1469-7610.1994.tb01162.x. [DOI] [PubMed] [Google Scholar]
- Lubke GH, Muthén B. Investigating population heterogeneity with factor mixture models. Psychological Methods. 2005;10(1):21–39. doi: 10.1037/1082-989X.10.1.21. [DOI] [PubMed] [Google Scholar]
- Lubke GH, Muthén B, Moilanen IK, McGough JJ, Loo SK, Swanson JM, & Smalley SL. Subtypes versus severity differences in attention-deficit/hyperactivity disorder in the northern Finnish birth cohort. Journal of the American Academy of Child and Adolescent Psychiatry. 2007;46(12):1584–1593. doi: 10.1097/chi.0b013e31815750dd. [DOI] [PubMed] [Google Scholar]
- Lykken DT. Statistical significance in psychological research. Psychological Bulletin. 1968;70:151–159. doi: 10.1037/h0026141. [DOI] [PubMed] [Google Scholar]
- MacCallum RC, Zhang S, Preacher KJ, Rucker DD. On the practice of dichotimization of quantitative variables. Psychological Methods. 2002;7(1):19–40. doi: 10.1037/1082-989x.7.1.19. [DOI] [PubMed] [Google Scholar]
- Macmann GM, Barnett DW. Discrepancy score analysis: A computer simulation of classification stability. Journal of Psychoeducational Assessment. 1985;4:363–375. [Google Scholar]
- Macmann GM, Barnett DW, Lombard TJ, Belton-Kocher E, Sharpe MN. On the actuarial classification of children: Fundamental studies of classification agreement. Journal of Special Education. 1989;23(2):127–149. [Google Scholar]
- Markon KE, Chmielewski M, Miller CJ. The reliability and validity of discrete and continuous measures of psychopathology: A quantitative review. Psychological Bulletin. 2011;137(5):856–879. doi: 10.1037/a0023678. [DOI] [PubMed] [Google Scholar]
- McDonald RP. A review of multivariate taxometric procedures: Distinguishing types from continua. Journal of Educational and Behavioral Statistics. 2003;28(1):77–81. [Google Scholar]
- Meehl PE. What social scientists don’t understand. In: Fiske DW, Shweder RA, editors. Metatheory in social science: Pluralisms and subjectivities. University of Chicago Press; Chicago, IL: 1986. pp. 315–338. [Google Scholar]
- Meehl PE. Factors and taxa, traits and types, differences of degree and differences in kind. Journal of Personality. 1992;60(1):117–174. [Google Scholar]
- Morris RD, Stuebing KK, Fletcher JM, Shaywitz SE, Lyon GR, Shankweiler DP, Shaywitz BA. Subtypes of reading disability: Variability around a phonological core. Journal of Educational Psychology. 1998;90(3):347373. [Google Scholar]
- Neale MC, Kendler KS. Models of comorbidity for multifactorial disorders. American Journal Of Human Genetics. 1995;57(4):935–953. [PMC free article] [PubMed] [Google Scholar]
- Plomin R, Kovas Y. Generalist genes and learning disabilities. Psychological Bulletin. 2005;131:592–617. doi: 10.1037/0033-2909.131.4.592. [DOI] [PubMed] [Google Scholar]
- Raudenbush SW. How do we study “what happens next?”. Annals of the American Academy of Political and Social Science. 2005;602(1):131–144. [Google Scholar]
- Rhee SH, Hewitt JK, Corley RP, Willcutt EG, Pennington BF. Testing hypotheses regarding the causes of comorbidity: Examining the underlying deficits of comorbid disorders. Journal of Abnormal Psychology. 2005;114(3):346–362. doi: 10.1037/0021-843X.114.3.346. [DOI] [PubMed] [Google Scholar]
- Rodgers B. The identification and prevalence of specific reading retardation. British Journal of Educational Psychology. 1983;53:369–373. doi: 10.1111/j.2044-8279.1983.tb02570.x. [DOI] [PubMed] [Google Scholar]
- Rourke BP, Finlayson MAJ. Neuropsychological significance of variations in patterns of academic performance: Verbal and visual-spatial abilities. Journal of Pediatric Psychology. 1978;3:62–66. doi: 10.1007/BF00915788. [DOI] [PubMed] [Google Scholar]
- Ruscio J, Haslam N, Ruscio AM. Introduction to the taxometric method: A practical guide. Lawrence Erlbaum; Hillsdale, NJ: 2006. [Google Scholar]
- Rutter M, Yule W. The concept of specific reading retardation. Journal of Child Psychology and Psychiatry. 1975;16:181–197. doi: 10.1111/j.1469-7610.1975.tb01269.x. [DOI] [PubMed] [Google Scholar]
- Shalev RS, Auerbach J, Manor O, Gross-Tsur V. Developmental dyscalculia: prevalence and prognosis. European Child and Adolescent Psychiatry. 2000;9:58–64. doi: 10.1007/s007870070009. [DOI] [PubMed] [Google Scholar]
- Shaywitz SE, Escobar MD, Shaywitz BA, Fletcher JM, Makuch R. Evidence that dyslexia may represent the lower tail of a normal distribution of reading ability. New England Journal of Medicine. 1992;326:145–150. doi: 10.1056/NEJM199201163260301. [DOI] [PubMed] [Google Scholar]
- Silva PA, McGee R, Williams S. Some characteristics of 9-year-old boys with general reading backwardness or specific reading retardation. Journal of Child Psychology and Psychiatry. 1985;26:407–421. doi: 10.1111/j.1469-7610.1985.tb01942.x. [DOI] [PubMed] [Google Scholar]
- Snowling MJ, Hulme C. Annual research review: The nature and classification of reading disorders: A commentary on proposals for DSM-5. Journal of Child Psychiatry and Psychology. 2012;53:593–607. doi: 10.1111/j.1469-7610.2011.02495.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanovich KE, Siegel LS. Phenotypic performance profile of children with reading disabilities: A regressionbased test of the phonological-core variable-difference model. Journal of Educational Psychology. 1994;86(1):24–53. [Google Scholar]
- Stuebing KK, Fletcher JM, Branum-Martin L, Francis DJ. Simulated comparisons of three methods for identifying specific learning disabilities based on cognitive discrepancies. School Psychology Review. 2012;41(1):3–22. [PMC free article] [PubMed] [Google Scholar]
- Stuebing KK, Fletcher JM, LeDoux JM, Lyon GR, Shaywitz SE, Shaywitz BA. Validity of IQ-discrepancy classifications of reading disabilities: A meta-analysis. American Educational Research Journal. 2002;39:469–518. [Google Scholar]
- U.S. Office of Education Assistance to states for education for handicapped children: Procedures for evaluating specific learning disabilities. Federal Register. 1977;42:G1082–G1085. [Google Scholar]
- Wagner RK, Torgesen JK, Rashotte CA. Comprehensive Test of Phonological Processing. PRO-ED; Austin, TX: 1999. [Google Scholar]
- Waller NG, Meehl PE. Multivariate taxometric procedures: Distinguishing types from continua. Sage; Thousand Oaks, CA: 1998. [Google Scholar]
- Willcutt EG, Betjemann RS, McGrath LM, Chhabildas NA, Olson RK, DeFries JC, Pennington BF. Etiology and neuropsychology of comorbidity between RD and ADHD: The case for multiple-deficit models. Cortex. 2010;46(10):1345–1361. doi: 10.1016/j.cortex.2010.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willcutt EG, Pennington BF, Duncan L, Smith SD, Keenan JM, Wadsworth S, Olson RK. Understanding the complex etiologies of developmental disorders: Behavioral and molecular genetic approaches. Journal of Developmental and Behavioral Pediatrics. 2010;31(7):533–544. doi: 10.1097/DBP.0b013e3181ef42a1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodcock RW, McGrew KS, Mather N. Woodcock-Johnson Psycho-Educational Battery III. Riverside; Itasca, IL: 2001. [Google Scholar]