Grouped False-Discovery Rate for Removing the Gene-Set-Level Bias of RNA-seq

Abstract

In recent years, RNA-seq has become a very competitive alternative to microarrays. In RNA-seq experiments, the expected read count for a gene is proportional to its expression level multiplied by its transcript length. Even when two genes are expressed at the same level, differences in length will yield differing numbers of total reads. The characteristics of these RNA-seq experiments create a gene-level bias such that the proportion of significantly differentially expressed genes increases with the transcript length, whereas such bias is not present in microarray data. Gene-set analysis seeks to identify the gene sets that are enriched in the list of the identified significant genes. In the gene-set analysis of RNA-seq, the gene-level bias subsequently yields the gene-set-level bias that a gene set with genes of long length will be more likely to show up as enriched than will a gene set with genes of shorter length. Because gene expression is not related to its transcript length, any gene set containing long genes is not of biologically greater interest than gene sets with shorter genes. Accordingly the gene-set-level bias should be removed to accurately calculate the statistical significance of each gene-set enrichment in the RNA-seq.

We present a new gene set analysis method of RNA-seq, called FDRseq, which can accurately calculate the statistical significance of a gene-set enrichment score by the grouped false-discovery rate. Numerical examples indicated that FDRseq is appropriate for controlling the transcript length bias in the gene-set analysis of RNA-seq data. To implement FDRseq, we developed the R program, which can be downloaded at no cost from http://home.mju.ac.kr/home/index.action?siteId=tyang.

Introduction

Over the past decade, microarrays have been the primary choice for genome-wide gene expression analysis. In recent years, RNA-seq has become a very competitive alternative to the microarray approach. RNA-seq refers to the use of high-throughput sequencing technologies to sequence cDNA to obtain information about a sample’s RNA content (http://en.wikipedia.org/wiki/RNA-Seq). In the RNA-seq experiment, purified RNA is amplified, shattered, and reverse transcribed into cDNA. These short pieces of cDNA are sequenced on a high-throughput platform such as Illumina HiSeq, SOLiD, or Roche 454, providing a list of short sequences called reads. Millions of short reads (25 to 300 bp) are then mapped to a library in which reference sequences are constructed, showing us which region each read comes from.¹ Note that the library can use the genome itself, annotated exons, or the dataset as its reference sequences. Because reads show higher reproducibility between technical replicates than microarray-based approaches do,^2,3 RNA-seq data are less noisy and thus more precise at detecting expression differences than microarrays are.

In the RNA-seq experiment, for a set of regions of interest on the genome, we count the number of reads mapped unambiguously to each region and use this count as a measure of expression of that region. For simplicity, we refer to such regions as genes. The expression levels of genes for RNA-seq datasets are represented as discrete read counts, arising from either a Poisson density or a negative binomial density, whereas those for microarrays are represented as continuous numbers. A gene-level P-value for differential expression among different conditions is obtained by several methods including edgeR,^4–6 DEGseq,⁷ DESeq,⁸ baySeq,⁹ and RPKM (reads per kilobase of exon model per million mapped reads)¹⁰ which are available in the R program software package. Kvam et al¹¹ compared the performance of these methods and insisted that baySeq has the highest true-positive rates at low rates of false positives.

A gene set of interest is a group of genes that share a common biological function, chromosomal location, or regulation. Gene sets are always given a priori according to the information provided by public databases such as Gene Ontology,¹² KEGG,¹³ Biocarta (http://www.biocarta.com), and GenMAPP (http://www.genmapp.org), by cytogenetic bands, by region of genomic sequence, or by the functional relationships among genes. The main purpose of gene-set analysis (GSA) seeks to identify the gene sets that are enriched in the list of the identified significant genes. The conventional GSA methods use either a gene-set enrichment score or gene-set-level statistic to measure the degree of enrichment, and compute its significance by comparison with random sampling.

In GSA, many tests are carried out to find the list of significant genes and the list of enriched gene sets so that the statistical significance of each gene-level test and each gene-set-level test is adjusted for multiple testing by controlling the false-discovery rate (FDR), which is defined as the proportion of null hypotheses that are rejected incorrectly.¹⁴ This is a necessary step in high-dimensional testing problems in genomic data analysis.

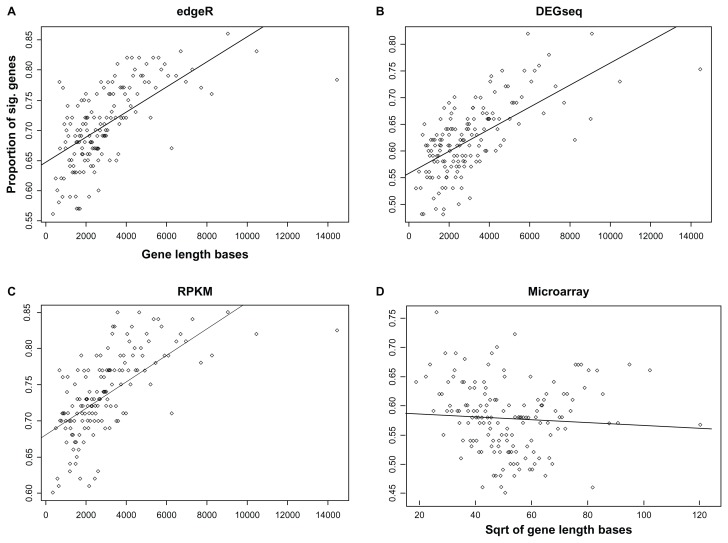
In RNA-seq experiments, the expected read count for a transcript is proportional to the gene’s expression level multiplied by its transcript length. Even when two transcripts are expressed at the same level, the differences in length will yield differing numbers of total reads. The characteristics of these RNA-seq experiments cause the gene-level-bias in which the proportion of significantly differentially expressed genes increases with the transcript length, as shown in Figure 1A–C and Figure 2. However, such increasing bias is not present in microarray data,^15,16 as shown in Figure 1D.

Figure 1.

Proportion of significant genes as a function of gene length (bases) for the dataset of Marioni et al. (A) edgeR with RNA-seq data, (B) DEGseq with RNA-seq data, (C) RPKM with RNA-seq data, and (D) t-test with microarray data. The proportion of significantly differentially expressed genes increases with the transcript length in RNA-seq data; such bias is not present in microarray data.

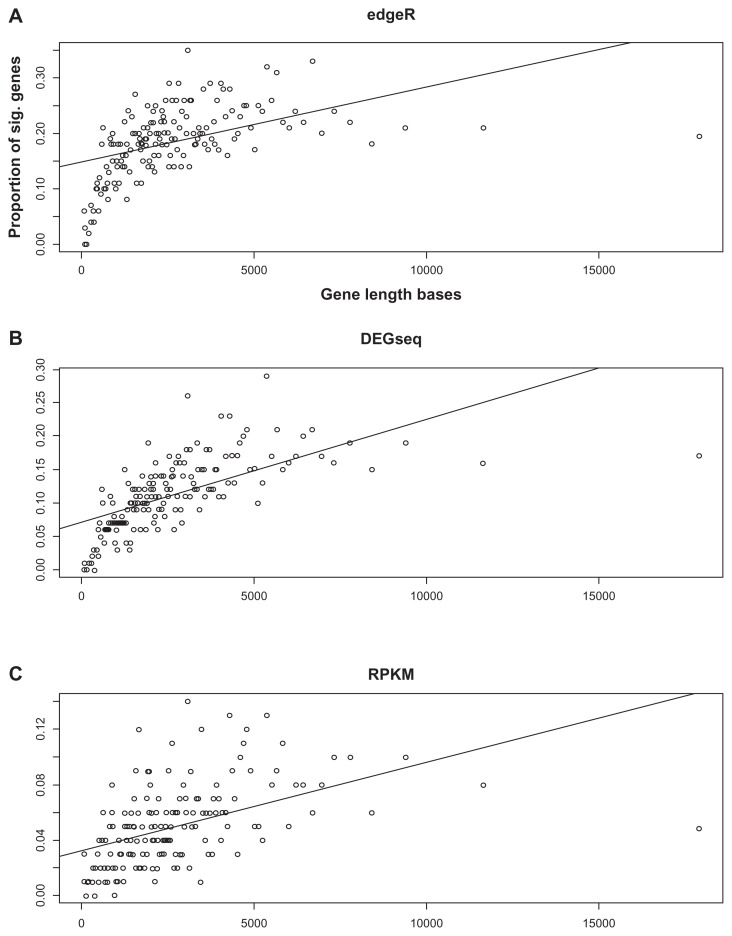
Figure 2.

Gene-level bias of the Li et al’s RNA-seq datasets. (A) edgeR, (B) DEGseq, (C) RPKM. The percentages of significant genes from the RNAseq data plotted as a function of the gene length bases. The probability of significant genes increases with the gene length.

The gene-level bias subsequently yields the gene-set- level bias in which a gene set with genes of long length will be more likely to show up as enriched than will a gene set with genes of shorter length. For instance, Fisher’s exact test is a commonly used method for identifying the enriched gene sets of microarray data. The test is based on the hypergeometric density as its null distribution under the standard assumption that all genes are independent and equally likely to be selected as differentially expressed under the null hypothesis.

Because the standard assumption does not hold for the RNA-seq data due to the gene-level bias, Fisher’s exact test clearly shows the gene-set-level bias (Fig. 3). Because the analysis of the microarray datasets (Fig. 1D) shows no evidence of gene-level bias,^15,16 gene sets containing long genes are not of biologically greater interest than gene sets with shorter genes. For accurately calculating the statistical significance of a gene-set enrichment score in RNA-seq, the gene-set-level bias should be removed. Ignorance of the gene-set-level bias in the GSA of the RNA-seq can be dangerous.

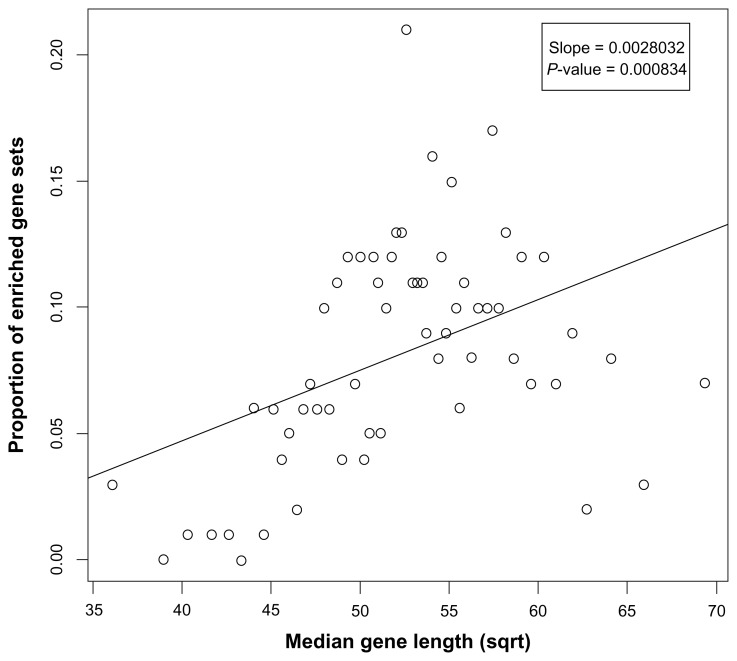
Figure 3.

Gene-set-level bias of the Li et al’s RNA-seq data. Percentages of enriched gene sets plotted as a function of the median transcript length of the gene sets. Gene sets with longer genes tend to be enriched.

In this paper, we present a new GSA method of RNA-seq, called FDRseq, which can properly remove the gene-set-level bias of the RNA-seq using the grouped FDR method. The statistical significance of each gene-set enrichment score is adjusted for multiple testing using the FDR. When calculating the FDR of each gene-set enrichment score, we sequentially order all gene sets according to their median gene lengths and then split these gene sets into four subgroups: short, moderately short, moderately long, and long genes. A gene set is only compared to gene sets in the same subgroup that have similar transcript lengths.

Controlling grouped FDR would give a similar number of enriched gene sets in each group so that the gene sets containing long genes are not more enriched than those with shorter genes. Therefore, the gene-set-level bias can be properly removed.

FDRseq

In FDRseq, when calculating the FDR of each gene-set enrichment score, we sequentially ordered all gene sets according to their median gene lengths and then split these gene sets into four subgroups: short, moderately short, moderately long, and long genes. We separately conducted FDR analysis within each subgroup at the same FDR level α, and then combined the test results from individual analyses. Sun et al¹⁷ and Efron¹⁸ showed that when FDR in each subgroup is controlled at the same level α, the overall FDR is controlled at α. Because a gene set is only compared with gene sets in the same subgroup that have similar median transcript lengths, controlling the FDR by grouping would give a similar number of enriched gene sets in each group. Several authors^19–22 have discussed the legitimacy of the grouped FDR method.

Random sampling with selection probability

With the list of significant genes, we determined which genes are significantly differentially expressed. Each gene is then respectively assigned 0 or 1, according to whether or not the gene is found to be significant. When N genes in the RNA-seq experiment are ordered sequentially according to their transcript lengths, genes can be divided into 10 bins, which are separated by the 10th, 20th, …, and 90th percentiles in the distribution of the transcript lengths of all genes. For each bin i (for i = 1, …, 10), we count ν_i, which is the number of significant genes in bin i. Let ν = ν₁ + … + ν₁₀ be the total number of significant genes. To quantify the weight probability of selecting bin i, we standardize the value by ν_i/ν. We call this the selection probability of bin i. It is the empirical weight probability that each gene will be included in the significant gene list by its transcript length. The probability is incorporated into the random sampling as follows. We first select a bin according to the selection probabilities. A gene is then randomly chosen from the selected bin. This implies that genes with similar length have an equal probability of being chosen as differentially expressed, but genes with differing lengths have different probabilities according to the empirical selection probability.

Gene-set enrichment score

We define a simple gene-set enrichment score to measure the degree of enrichment. Suppose that K predefined gene sets of S₁, …, S_K are under consideration. If there exist r_k significant genes of m_k genes in a gene set S_k (k = 1, …, K), then the gene-set enrichment score is defined as

$$E_k=r_k/m_k;$$

this measures the size of the overlap between S_k and the list of significant genes. Because GSA aims to identify the gene sets that are enriched in the list of the identified significant genes, a larger E_k indicates greater enrichment of S_k.

Grouped false-discovery rate to remove gene-set level bias

We sequentially ordered K pre-defined gene sets according to their median gene lengths. These K gene sets were then divided into C1 to C4, which were further divided into the 25th, 50th, and 75th percentiles in the distribution of the median transcript lengths of all the gene sets. Thus, C1, C2, C3, and C4 represent the subgroup of gene sets with short, moderately short, moderately long, and long genes, respectively. Then each gene set is compared with gene sets in the same subgroup that have a similar transcript length to that gene set.

The statistical significance of each gene-set enrichment score is corrected for multiple testing by controlling the FDR. To estimate FDR of E_k, we implement the permutation plug-in method.^1,23,24 In R random samples, each random sample is obtained by randomly selecting a set of genes, as many as the number of observed significant genes, according to the proposed selection probability. Let E_k^x (x=1…,R) represent the E_k value in the x-th randomization of R random experiments, and let E_k⁰ be the observed value E_k. When S_k ε C_i, the grouped FDR of E_k is given by

$${\text{FDR}}_k=\frac{{\sum }_{x=1}^R{\sum }_{y=1,S_y\in C_i}^{K}I(E_k^0\le E_y^x)/R}{\text{Rank\hspace{0.17em}of\hspace{0.17em}}{E}_k^0\hspace{0.17em}\text{in\hspace{0.17em}}{C}_i}.$$ (1)

The numerator represents a count of how many simulated E_k values are greater than or equal to the observed experimental E_k⁰ value occurring in a list of gene sets of C_i. From this, the average expected value is calculated. The denominator denotes the position of gene set S_k in C_i, that is, it is the number of gene sets considered as enriched in C_i

When FDR_k,< α, the gene set S_k is enriched at the level of α. When FDR in each C_i is controlled at the same level α, the overall FDR is controlled at α.^17,18 Finally, we combine the obtained false-discovery rates over C1–C4 to rank K gene sets.

Results

For numerical examples, we used the two RNA-seq datasets of Marioni et al² and Li et al,²⁵ which have been widely used in the literature on RNA-seq data analysis.

Marioni et al dataset

The study by Marioni et al² was designed to compare the RNA-seq experiment with the microarray experiment.

The microarray data were generated from human kidney and liver tissues, with each tissue profiled on Affymetrix HG-U133 Plus 2.0 arrays in three technical replicates. The microarray dataset contained 17,708 genes. For identifying differentially expressed genes between the kidney and liver, we used the P-values from simple t-test statistics. We then generated a list of 8,730 significant genes with a false-discovery rate of 0.01. For comparison purposes, the Affymetrix gene IDs of the microarray dataset were mapped to the Ensembl gene IDs of the RNA-seq dataset using the biomaRt (http://www.biomart.org). When multiple Affymetrix probe sets had the same Ensembl gene ID, the median expression of these probe sets was used as the expression level for the Ensembl gene ID.

An RNA-seq dataset was generated for the same human liver and kidney tissues with five runs per tissue using the Illumina Genome Analyzer. The RNA-seq dataset contained 32,000 genes, but many of them had no more than five reads in total. These genes were removed. We also removed genes that were not on the Affymetrix U133 plus 2.0 microarray for comparison purposes.

Human gene lengths were obtained from the UCSC genome browser (http://genome.ucsc.edu/cgibin/hgTables). We used R-package ‘geneLen DataBase’, which provides the mapping between an Ensembl gene ID of the RNA-seq dataset and its associated transcripts. Genes were removed if their transcript lengths were not available in the database. Finally, 15,097 genes were left for analysis.

Each gene-level P-value for differential expression between the liver and kidney tissue was obtained using edger.^4–6 These P-values were corrected for multiple testing, and the FDR was set to 0.01. We obtained a list of 10,697 significant genes in the RNA-seq dataset. For comparison, DESeq⁸ and RPKM¹⁰ were also applied to the dataset. In Figure 1, the percentages of significant genes from the RNA-seq and the microarray dataset are respectively plotted as a function of gene length. Each point represents a bin of 300 genes with similar transcript length. Figure 1A–C show a strong increasing pattern representing the gene-level bias of the RNA-seq, whereas Figure 1D shows no systematic increasing trend between the square root of the gene length and the differential expression in the microarray data. Rather, Figure 1D interestingly shows a weak decreasing trend, which is the opposite pattern to the gene-level bias in the RNA-seq data.

Hereafter, the following results were based on the significant genes obtained from edgeR. We found 14,681 gene sets matched with human genes from the Gene Ontology Consortium database and discarded the gene sets with fewer than five and those with more than 500 genes, because gene sets that are too small or too large are often excluded from analyses in practice.²⁶ We then analyzed 6,805 gene sets from the database. With these gene sets, we applied (I) Fisher’s exact test using a hypergeometric distribution test to the microarray dataset, (II) Fisher’s exact test using hypergeometric distribution testing to the RNA-seq dataset, (III) GOseq²⁷ using the Wallenius distribution to the RNA-seq dataset, (IV) GOseq using probability weighting function to the RNA-seq dataset, (V) Gao et al’s method²⁶ to the RNA-seq dataset, and (VI) FDRseq to the RNA-seq dataset. For (I)–(VI), the gene sets were ranked based on the FDRs, and the top 600 gene sets were respectively selected as enriched. In Figures 4 and 5, we considered (I) as the standard method and compared (I) with (II)–(VI).

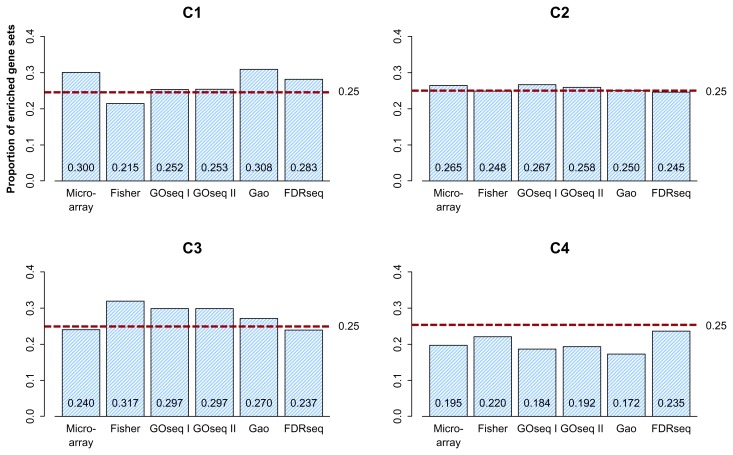
Figure 4.

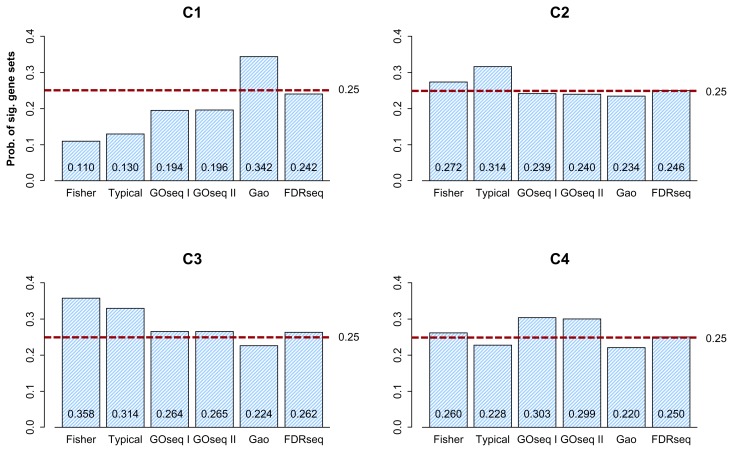
Proportion of enriched gene sets as a function of the median transcript length of gene sets. (I) ‘Microarray’ represents Fisher’s exact test using a hypergeometric distribution test to the microarray dataset, (II) ‘Fisher’ represents Fisher’s exact test using hypergeometric distribution testing to the RNA-seq dataset, (III) ‘GOseq I’ represents GOseq using the Wallenius distribution to the RNA-seq dataset, (IV) ‘GOseq II’ represents GOseq using a probability weighting function to the RNA-seq dataset, (V) ‘Gao’ represents Gao et al’s method applied to the RNA-seq dataset, and (VI) ‘FDRseq’ represents FDRseq applied to the RNAseq dataset. C1, C2, C3, and C4 respectively represent the category of gene sets with short, moderately short, moderately long, and long genes. FDRseq and Gao are closer to the standard method (I) than the other methods are. Furthermore, FDRseq has approximately 25% enriched gene sets over the range of C1–C4. This indicates that FDRseq properly controls the gene-set-level bias of the RNA-seq data.

Figure 5.

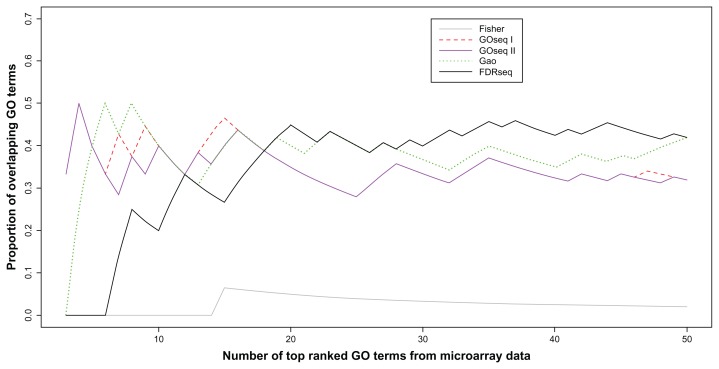
Proportion of overlapping gene sets between the microarray and RNA-seq. (I) ‘Standard’ represents Fisher’s exact test using a hypergeometric distribution test for the microarray dataset, (II) ‘Fisher’ represents Fisher’s exact test using hypergeometric distribution testing for the RNA-seq dataset, (III) ‘GOseq I’ represents GOseq using the Wallenius distribution to the RNA-seq dataset, (IV) ‘GOseq II’ represents GOseq using a probability weighting function for the RNAseq dataset, (V) ‘Gao’ represents Gao et al’s method applied to the RNA-seq dataset, and (VI) ‘FDRseq’ represents FDRseq applied to the RNA-seq dataset. FDRseq and Gao had more overlap with (I) the standard method than with the other methods.

In (III) and (IV), GOseq (http://bioinf.wehi.edu.au/software/goseq)²⁷ respectively used the Wallenius distribution and the probability weighting function rather than the hypergeometric distribution as the null distribution for Fisher’s exact test. The Wallenius distribution is a generalization of the hypergeometric distribution in the case where the probability of choosing a gene within or outside of a gene set is defined as the non-central parameter within and outside of that gene set. It indicates that all genes within the gene set have the same probability of being chosen, but this probability is different from the probability of choosing genes outside of this gene set. In (V), the Gao et al’s method²⁶ used the square root of the gene length as Wallenius’s non-central parameter which is different from GOseq.²⁷

We sequentially ordered 6,805 gene sets according to their median gene lengths and then divided these gene sets into C1 through C4, which were separated further at the 25th, 50th, and 75th percentiles in the distribution of the median transcript lengths of all gene sets. Figure 4 shows the percentages of enriched gene sets plotted as a function of the median transcript length of the gene sets, where C1–C4 represent the gene sets with short, moderately short, moderately long, and long genes, respectively. We calculated the sum of proportion differences over C1–C4 between the standard method (I) vs. each of (II)–(VI), yielding results of 0.204 (I vs. II), 0.118 (I vs. III), 0.114 (I vs. IV), 0.076 (I vs. V), and 0.080 (I vs. VI). FDRseq (VI) and Gao et al’s method (V) have lower values of 0.080 and 0.076, respectively, indicating that FDRseq and Gao et al’s method are, overall, closer to the standard method than are other methods. Furthermore, FDRseq has approximately 25% enriched gene sets over the range of C1–C4, which indicates that FDRseq properly controls the gene-set-level bias of RNA-seq data.

In Figure 5, the proportions of overlapping gene sets between (I) vs. each of (II)–(VI) are plotted for the 50 top-ranked gene sets. The figure represents that FDRseq and the Gao et al method²⁶ had more overlap with the standard method (I) than did the other methods.

Li et al dataset

In the RNAseq dataset of Li et al,²⁵ the prostate cancer cell line LNCap was treated with mock/DHT. For the mock-treated cells, there were four runs totaling 10 million reads. For the DHT-treated cells, there were three runs totaling 7 million reads. All seven runs were technical replicates.

The dataset originally contained 49,506 human genes, but many of them had no more than five reads total. These genes were removed, leaving 16,141 genes for further analysis. Each gene-level P-value for differential expression between the treated and untreated samples was obtained using edgeR.^4–6 The P-values from edgeR were adjusted for multiple testing, and the FDR was set to 0.05. We then obtained a list of 2,986 significant genes in the RNA-seq dataset. The genes were grouped according to their transcript length, with 300 genes in each bin. For comparison, DESeq⁸ and RPKM¹⁰ were also applied to the dataset. Figure 2 shows the percentages of significant genes from the RNAseq data plotted as a function of the gene length. The figure clearly shows the gene-level bias; the probability of significant genes increased with the gene length.

Hereafter, the following results were based on the significant genes obtained from edgeR. We found 13,929 matched gene sets with the human genes from the Gene Ontology Consortium database and discarded the gene sets with fewer than five or more than 500 genes; gene sets too small or too large are often excluded from analyses in practice.²⁶ We then analyzed 6,187 gene sets further. To calculate the statistical significance of each gene-set enrichment, (I) Fisher’s exact test using the hypergeometric distribution, (II) the typical gene-randomization sampling (described in Discussion Section) with 100,000 repetitions, (III) GOseq²⁷ using the Wallenius distribution to the RNA-seq dataset, (IV) GOseq using a probability weighting function, (V) Gao et al’s method,²⁶ and (VI) FDRseq were applied to the 6,187 gene sets. For (I)–(VI), the gene sets were ranked based on the FDRs, and the top 500 gene sets were selected as enriched.

In (I), Fisher’s exact test was based on the hypergeometric density under the standard assumption that the probability of each gene entering the significant gene list was the same. Figure 3 shows the percentages of enriched gene sets plotted as a function of the median transcript length of the gene sets. Because the equal selection probability does not hold for the RNA-seq data due to the gene-level bias as shown in Figure 2, the test tends to be enriched for the gene sets with longer genes, and Figure 3 clearly shows the gene-set-level bias of the RNA-seq data.

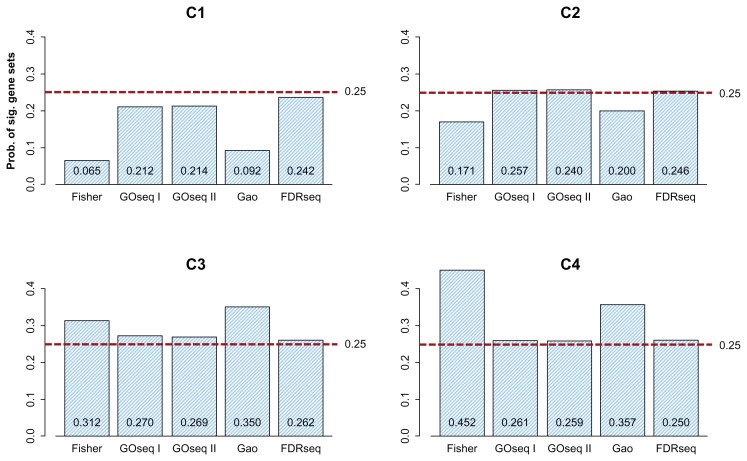
Figure 6 shows the percentages of enriched gene sets plotted over the range C1–C4. As we expected, FDRseq provides a closer approximation to 25% of the enriched gene sets across C1–C4 than the other methods do. This indicates that FDRseq gives a similar number of enriched gene sets to each group, which properly controls the gene-set-level bias of the RNA-seq data.

Figure 6.

Proportion of enriched gene sets as a function of the median transcript length of the gene sets. (I) ‘Fisher’ represents Fisher’s exact test using the hypergeometric distribution, (II) the typical gene-randomization sampling (described in the Discussion) with 100,000 repetitions, (III) ‘GOseq I’ represents GOseq using the Wallenius distribution, (IV) ‘GOseq II’ represents GOseq using a probability weighting function, (V) ‘Gao’ represents Gao et al’s method, and (IV) ‘FDRseq’. C1, C2, C3, and C4 represent the category of gene sets with short, moderately short, moderately long, and long genes, respectively. The percentages of enriched gene sets plotted over the range C1–C4. FDRseq provides a closer approximation to 25% of the enriched gene sets across C1–C4 than the other three methods do. FDRseq gives a similar number of enriched gene sets to each group, which allows proper control over the gene-set- level bias of the RNA-seq data.

Simulation study for the performance of FDRseq

We conducted a simulation study to compare FDRseq with the other methods, with respect to their suitability for removing the gene-set-level bias. In this study, we used 16,075 genes and 6,805 gene sets as given in the numerical example of Marioni et al.² Human gene lengths were obtained from the UCSC genome browser (http://genome.ucsc.edu/cgibin/hgTables) for each combination of human genome and Ensembl gene ID of the RNAseq.

We randomly sampled 16,075 gene-level P-values according to the gene length; 0.1 * Uniform (0, 0.01) +0.9 * Uniform (0.01, 1) in the first quartile of the gene length distribution (C1); 0.2 * Uniform (0, 0.01) + 0.8 * Uniform (0.01, 1) in the middle two quartiles of the distribution (C2 and C3); 0.3 * Uniform (0, 0.01) +0.7 * Uniform (0.01, 1) in the fourth quartile (C4), where Uniform(a,b) represents uniform density within the two boundaries of a and b. The FDR for testing the significance of each gene was set at 0.01. The simulated P-values clearly represent the bias pattern that the proportion of significantly differentially expressed genes increases with the gene length. With these simulated P-values, we analyzed 6,805 gene sets by applying (I) Fisher’s exact test using the hypergeometric distribution, (II) GOseq using the Wallenius distribution to the RNA-seq dataset, (III) GOseq using a probability weighting function for the RNA-seq dataset, (IV) Gao et al’s method to the RNA-seq dataset, and (V) FDRseq. Then, the top 500 ranked gene sets were selected as enriched.

One thousand simulations were executed to obtain the empirical distribution for the proportion of enriched gene sets as a function of the median transcript length of the gene sets. Figure 7 shows the simulated results for the percentages of enriched gene sets plotted as a function of the median transcript length of the gene sets. FDRseq has approximately 25% enriched gene sets over the range of C1–C4. This indicates that FDRseq more appropriately controls the gene-set-level bias of RNA-seq data than GOseq and Fisher’s exact test do.

Figure 7.

Simulated results for gene-set-level bias. (I) ‘Fisher’ represents Fisher’s exact test using the hypergeometric distribution, (II) the typical gene-randomization sampling (described in the Discussion) with 100,000 repetitions, (III) ‘GOseq I’ represents GOseq using the Wallenius distribution, (IV) ‘GOseq II’ represents GOseq using probability weighting function, (V) Gao represents ‘Gao et al’s method’²⁶, and (IV) FDRseq. Proportion of enriched gene sets as a function of the median transcript length of the gene sets. C1, C2, C3, and C4 represent the category of gene sets with short, moderately short, moderately long, and long genes, respectively. FDRseq has approximately 25% enriched gene sets over the range of C1–C4. This indicates that FDRseq more appropriately controls the gene-set-level bias of RNA-seq data compared with other methods.

Discussion

In the typical gene-randomization sampling scheme, the P-value for enrichment of a gene set of interest, S_k (for a total of m_k genes), was generated using random sampling of m_k genes from the full set of all genes, with an equal selection weight for each gene. For each of the R repetitions, we counted the number of significant genes in the generated gene set by comparison with the number of observed significant genes of S_k. The P-value for enrichment of S_k was calculated as a fraction of the resampled gene sets in that the number of significant genes was greater than or equal to the number of observed significant genes. The statistical significance of each P-value was corrected for multiple testing by controlling the FDR. The total number of random samples of typical sampling was K (number of gene sets) × R (number of repetitions). When K is large, the typical scheme requires heavy, time- consuming computation. In contrast, FDRseq performed only R repetitions, where each random sample was obtained by randomly selecting a set of genes as large as the observed significant genes according to the proposed selection probability. The computational reduction afforded by FDRseq is formidable.

The gene-length bias is inherent to the nature of RNA-seq because there are essentially more reads for longer genes. In GSA, the gene-level bias clearly yields the gene-set-level bias in which a gene set with genes of long length will be more likely to show up as enriched than will a gene set with genes of shorter length. Correction for the gene-length-bias is necessary. For calculating the statistical significance of each gene-set enrichment score, the conventional GSA methods established for the microarray data, such as Fisher’s exact test, gave biased results for RNA-seq data. We have provided a new GSA to properly take into account the bias of RNA-seq data. Numerical results and simulations indicated that FDRseq is appropriate for controlling bias in the gene-set analysis of RNA-seq data. Because the main purpose of executing GSA analysis is to rank the gene sets based on pathways or GO terms for follow-up research, FDRseq would provide an accurate list of enriched gene sets.

Although FDRseq was originally developed to accurately calculate the statistical significance of each gene-set enrichment in the RNA-seq data, the technique can also be applied directly to the gene-set analysis of the microarray data. In this sense, FDRseq is a unified gene-set analysis method for assessing gene-set enrichment in either microarray data or RNA-seq data.

Zheng et al²⁸ interestingly insisted that gene expression levels of RNA-seq are also biased with respect to other factors, such as GC content and dinucleotide frequencies. However, it is not clear to us how GC content and dinucleotide frequencies affect the GSA of RNA-seq or how to remove their corresponding bias in conducting the GSA of RNA-seq. More research is needed on this topic.