Surface Adsorbate Fluctuations and Noise in Nanoelectromechanical Systems

Abstract

Physisorption on solid surfaces is important in both fundamental studies and technology. Adsorbates can also be critical for the performance of miniature electromechanical resonators and sensors. Advances in resonant nanoelectromechanical systems (NEMS), particularly mass sensitivity attaining the single-molecule level, make it possible to probe surface physics in a new regime, where a small number of adatoms cause a detectable frequency shift in a high quality factor (Q) NEMS resonator, and adsorbate fluctuations result in resonance frequency noise. Here we report measurements and analysis of the kinetics and fluctuations of physisorbed xenon (Xe) atoms on a high-Q NEMS resonator vibrating at 190.5 MHz. The measured adsorption spectrum and frequency noise, combined with analytic modeling of surface diffusion and adsorption–desorption processes, suggest that diffusion dominates the observed excess noise. This study also reveals new power laws of frequency noise induced by diffusion, which could be important in other low-dimensional nanoscale systems.

Physisorption of atomic or molecular species is ubiquitous in virtually all circumstances where solid–gas interfaces exist (e.g., catalysis, adhesion). In physics, directly observing and manipulating individual adsorbed atoms on ultraclean surfaces represents a significant experimental feat.¹ Engineering of atomic and molecular structures on certain surfaces also plays important roles in emerging applications including programmable self-assembly,^2,3 nanoscale lithography,⁴ and nanotribology.⁵ For solid-state transducers, especially high-precision detectors and sensors, surface adsorbate can have important influences on device performance.⁶ Electromechanical resonators with high quality factor (Q), particularly quartz crystal microbalances (QCMs), are widely used to measure the mass, and other physical and electrochemical properties of the adsorbed layers, by monitoring changes of the QCM resonance frequency, Q factor, or amplitude.^7,8 Resonant nanoelectromechanical systems (NEMS) sensors have recently demonstrated significantly enhanced mass sensitivities, down to the level of several, or even single, noble gas atoms,^9–11 representing an improvement up to 10¹²-fold over a conventional QCM. Such sensitivity levels provide the new opportunity of employing NEMS to directly probe the effects of surface adsorbate, on very small surface areas (typically of the order of only ~100 nm × 1 µm) and in the submonolayer regime. This approach can effectively complement and advance today’s prevailing experimental techniques in surface science (e.g., spectroscopy and ellipsometry for surface thermodynamics, atomic force microscopy, scanning tunneling microscopy, quasielastic atom scattering for surface diffusion, and QCM for interfacial friction).¹² As an initial step toward this new paradigm, in this work we employ a high-Q, very high frequency (VHF) NEMS resonator to investigate the behavior of physisorbed xenon (Xe) atoms, by performing precise measurements of the excess frequency noise that arises from statistical fluctuations of the adsorbed atoms on the resonator surface.

The core of our experimental apparatus (Figure 1a) consists of a NEMS resonator and a micro gas nozzle, well aligned and in close proximity. The NEMS resonator is a doubly clamped beam with dimensions 2.3 µm (L) × 150 nm (w) × 100 nm (t). It is surface-nanomachined from a 100 nm silicon carbide (SiC) layer on silicon (Si) substrate, in a process detailed elsewhere.¹³ Metallization and passivation of the device consist of a 30 nm film of thermally evaporated aluminum (Al) capped with 5 nm titanium (Ti). At least part of the top Ti film upon exposure to air turns into native oxide (TiO₂),¹⁴ which is not only an excellent passivation layer but also a popular surface for biochemical species and a remarkable catalyst.^15,16

The device is electrically connected onto a dedicated chip carrier (with an embedded circuit board) and mechanically and thermally anchored to a massive sample stage (brass, gold plated). The sample stage is loaded into an ultrahigh-vacuum (UHV) cryostat, first pumped down at room temperature overnight (to ~5 × 10⁻⁷ Torr) and then cooled down in liquid helium (LHe). The device temperature is precisely measured and regulated by a calibrated on-board thermometer and a closed-loop temperature controller. We employ the magnetomotive scheme^9,13 to excite the device into resonance and detect its response. The orientation of the magnetic field is such that the out-of-plane flexural modes are excited; the calculated modal mass of the resonator is M_eff ≈ 96 fg. Figure 1c displays the measured response at a temperature T ≈ 58 K, showing the sharp (Q ≈ 5620) fundamental-mode flexural resonance at a frequency f₀ ≈ 190.5 MHz, corresponding to an effective stiffness k_eff ≈ 145 N/m. We have incorporated the NEMS resonance signal readout (Figure 1b) into a low-noise, frequency-modulation phase-locked loop (FM PLL) circuitry.^9,17 This enables frequency locking and tracking of the resonance, hence real-time monitoring of the frequency variations that reflect the thermodynamic effects of adsorbates on the device surface. Prior to investigating the real-time behavior of surface adsorbates, we perform extensive tests and careful calibrations of the device response to a steadily increasing mass-load using the FM PLL technique. Figure 1d shows the calibration of the excellent mass responsivity of the device, ℛ ≡ |∂f₀/∂M| = 0.99 Hz/zg [i.e., a resonance frequency shift of ~1 Hz per zg (10⁻²¹ g) of loaded mass].

Adsorbates are delivered to the NEMS resonator via a micro gas nozzle (Figure 1a) fed by a gas delivery system connected to a buffer chamber. The nozzle has a circular aperture of 300 µm in diameter. It operates at low gas density as an effusive cell¹⁸ to produce an atomic beam of Xe impinging onto the NEMS surface. The cell’s gas kinetics determines the Xe atoms impinging rate I (atoms per unit area per unit time), which can be converted into an effective pressure of the impinging gas phase above the device, via p = I(2πm_Xek_BT)^1/2, where k_B is the Boltzmann constant and T is the device temperature. In this study, the calibrated constant flux delivered by the nozzle is I = 2.7 × 10¹⁷ atoms/(m²·s). This corresponds to a local effective pressure of p = 6.8 × 10⁻⁸ Torr at a device temperature T = 60K. The cross section area of the device exposed to the well-aligned incoming atomic beam is A_D = Lw = 3.45 × 10⁻¹³ m². A flat surface with this area can accommodate an ideal close-packed monolayer of N_a,est ≈ 2.2 × 10⁶ Xe atoms (with a Lennard-Jones diameter d_Xe ≈ 0.41 nm); N_a,est is thus the estimated number of available adsorption sites in the limit of an ideal, flat, and clean surface.

We choose to introduce Xe gas to the NEMS surface due to its relatively large atomic mass (m_Xe = 131.3 amu) and for its record as a classic prototype for studying physisorption in surface science.¹⁹ Existing Xe physisorption studies, however, are primarily limited to ideal, smooth, often specially treated metal surfaces,^12,19 where a realistic description of the surface processes can be tackled in quantitative analyses or computer simulations.¹⁹ In ordinary and more practical situations involving nonideal, nonmetal, and disordered surfaces, understanding of adsorbates dynamics is particularly poor; quantitative studies and experimental approaches are greatly needed. On the surface of a resonating NEMS device, as sketched in Figure 1e, the behavior of Xe atoms is intriguing and may include both adsorption–desorption (out-of-plane) and surface diffusion (in-plane) processes. Because conventional sensors lack the necessary sensitivity, no experiment has been carried out to investigate the contribution of these processes to resonance frequency fluctuations. Note that the frequency variations depend not only on the total number of adsorbed Xe atoms, but also on their distribution and fluctuations on the device surface (e.g., along the length of the device, in this study).

We first measure the adsorption spectrum N(T), i.e., number of adsorbed Xe atoms as a function of the regulated device temperature T. As the device is cooled down, N(T) increases. We call this process temperature-programmed adsorption (TPA, see Supporting Information). Such variations are precisely measured as the resonance frequency change Δf_m due to the mass-loading effect of the adsorbates, Δf_m = N(T)ℛm_Xe. Figure 2 demonstrates the measured adsorption spectrum and effective surface overage in the temperature range T ≈ 58–80 K. For a given incoming atom flux, the TPA process is highly repeatable and reversible, by regulating the device temperature back and forth in the appropriate temperature range. Unlike conventional Langmuir isotherm adsorption spectra (i.e., surface coverage versus pressure of the gas phase, at constant surface temperature), the data here are closer to isobars (number of adsorbates versus device temperature, at constant pressure of the gas phase).²⁰ We note that, in our measurements with the above value of the atom flux, when the device is cooled down to a temperature lower than T ≈ 56 K, the FM-PLL consistently experiences such a sudden and steep frequency shift that it cannot sustain the locking and tracking of the NEMS resonance; we call this phenomenon “PLL runaway”. We presume that the inflection point before the onset of this behavior represents an equivalent one-monolayer coverage, beyond which very fast accumulation of Xe atoms occur on the surface, leading to the so-called “wetting”-like behavior (i.e., abrupt formation of multilayer Xe films on device surface, which is dramatic and the associated frequency shift causes the PLL runaway).²¹ The measured frequency shift before PLL runaway is Δf_mon ≈ 590 kHz and the corresponding number of atoms is N_a,exp ≈ 2.7 × 10⁶. This value strongly supports our identification of PLL runaway with the completion of a monolayer. The slightly higher value (~20%) compared to our prediction N_a,est for an ideally flat surface is very reasonable considering the small but nonzero roughness of the device surface, and the uncertainty in determining the device geometry and actual surface area. After repeatedly experiencing the PLL runaway and identifying the temperature at which it occurs, we focus our experiments in the range T ≈ 58–80 K where the TPA is highly reversible and easily controllable.

The measured temperature-regulated surface coverage (Figure 2a), θ(T) = N(T)/N_a,exp, helps to reveal the thermodynamics between the surface adsorbates and the gas phase. The adsorbing rate (atoms per unit area per second), r_a = sI, is a fraction of the atoms impinging rate, with the ratio s being the sticking coefficient. We take s = 1 as customarily done for Xe impinging on very cold surfaces.²² We model the temperature dependence of the rate of atoms leaving the surface as a thermally activated process following the Arrhenius law, that is, by a surface-detaching rate r_d = ν_a exp(−E_a/k_BT), where E_a is the activation energy and v_a the attempt frequency. The steady-state balance between the gas phase and surface adsorbates dictates r_aA_D = Nr_d, hence N(T) = (sIA_D/ν_a)exp(E_a/k_BT). As shown in Figure 2b, this simple model neatly fits the experimental data, yielding E_a ≈ 63.1 meV (±0.23 meV), and v_a ≈ 1.23 × 10⁴ Hz(±0.05 × 10⁴ Hz). Note the v_a value from the fit is less reliable than the E_a value (v_a is more sensitive to fitting uncertainties, also depending on accurate determination of several experimental parameters). The extracted E_a is substantially smaller than the desorption energy reported for Xe on TiO₂ surfaces,^23,24 in the range of E_des ~ 200–300 meV (note that reported desorption energy data for Xe on crystalline metals or graphite are also in this range^22,25,26). We recall that atoms can leave the device surface via either desorption into vacuum or lateral diffusion (Figure 1d); both processes can be described by an Arrhenius equation, where however the activation energy of the diffusion process is generally much smaller. Indeed, we find the measured activation energy to be in good agreement with typical reported values of the lateral diffusion energy barrier E_diff of Xe on surfaces (e.g., E_diff ≈ 52.1 meV,²⁵ 54 meV,²⁷ moderately higher than the Xe–Xe binding energy, ~20 meV). This suggests that in our experiment the dynamic balance of surface adsorbates could be primarily between the adsorbing atoms from the nozzle and the atoms diffusing off the NEMS resonator.

To gain more insight beyond the above steady-state picture provided by the TPA and the initial surface kinetics analysis, we further carefully probe the fluctuations of the surface adsorbates by investigating the noise behavior of the VHF NEMS resonator while tuning the surface coverage via the device temperature. We measure the frequency instability of the NEMS resonator, quantified by the Allan deviation,²⁸ σ_A(τ_A)=[1/(2(N − 1)) ${\sum }_{i=1}^N{({({\overline{f}}_{i+1}-{\overline{f}}_i)/f_0)}^2]}^{1/2}$, with f̄_i being the average frequencies measured over an averaging time τ_A = 1 s by employing the FM-PLL technique. We first measure the baseline instability without the Xe flux (Allan deviation σ_A,sys); and then again with the Xe flux. Figure 3 shows the measured Allan deviation as a function of device temperature. The axis on the right shows the corresponding mass fluctuations (at zeptogram scale) set by the frequency instability. The instability measured without Xe flux represents the noise floor of the system and slightly decreases as temperature is lowered. This corresponds to the mild but steady increase of the Q factor that we observe upon cooling the device in this temperature range (see Supporting Information). With the introduction of surface adsorbates, excess instability arises, clearly noticeable in Figure 3 for T < 70 K. Also visible are a few small peaks distributed in the Allan deviation plot. The fact that these small peaks appear in the data with surface adsorbates but not in the noise floor data suggests the existence of some interesting surface processes. We hypothesize that they may be related to the details of certain collective behavior of the adsorbed atoms, which could be dependent on roughness and structural irregularity of the surface (e.g., terraces, defects).

To understand the trend displayed by the measured data in Figure 3, we have developed analytic models for the two processes, adsorption–desorption and surface diffusion, that we consider relevant. We first examine the frequency noise due to adsorption–desorption. The adsorption–desorption noise model (see Supporting Information) deals with nondiffusive (i.e., laterally immobile) adsorbates at submonolayer coverage, in a fashion similar to an earlier work modeling surface contaminants on a quartz crystal resonator.²⁹ Figure 2a shows the measured effective surface coverage θ(T) and the surface occupation deviation σ_occ = [N(N_a − N)]^1/2/N_a = [θ(1 − θ)]^1/2 (note that the surface occupation variance is ${\sigma }_{\text{occ}}^2\equiv r_{\text{ad}}{r}_{\text{des}}/{(r_{\text{ad}}+r_{\text{des}})}^2=N(N_a-N)/{N_a}^2)$, where N_a = N_a,exp is the number of adsorption sites, and r_ad and r_des are pure adsorption and desorption rates per adsorption site (in Hz), respectively. Clearly σ_occ has a maximum at θ = 1/2. Assuming pure adsorption–desorption, a characteristic correlation time can be defined for this process as τ_r = 1/(r_ad+r_des) = N/(sIA_D), which is computed using the measured data and is plotted in the inset of Figure 2b. This leads to the excess Allan deviation σ_A,ad–des(τ_A) ≈ 0.29σ_occ·(N_a)^1/2(m/M)(τ_A/τ_r)^1/2 in our experimental regime (see Supporting Information). Therefore, considering only adsorption–desorption noise and system noise, the total expected instability is ${\sigma }_{\mathrm{A},\text{ad},\text{total}}={({\sigma }_{\mathrm{A},\text{sys}}^2+{\sigma }_{\mathrm{A},\text{ad}–\text{des}}^2)}^{1/2}$. As displayed in Figure 3 (dark gray lines, note that σ_A,sys ≫ σ_A,ad–des hence σ_A,ad,total ~ σ_A,sys, hardly distinguishable), the estimated adsorption–desorption noise contribution is much lower even than the system noise floor, thus cannot account for the measured frequency instability in the presence of a Xe flux.

This predicted low adsorption–desorption noise and the above kinetics data (E_a ~ E_diff ≪ E_des) suggest that desorption cannot be the dominant mechanism of Xe atoms leaving the device surface. Hence we have developed a model to analyze noise due to Xe atoms diffusion on the device surface (see details in Supporting Information). We compute the autocorrelation function G(τ) of the fractional frequency fluctuations y(t) ≡ δf(t)/f₀ induced by Xe atoms diffusion

$$G(\tau )=\frac{\langle \delta f(t)·\delta f(t+\tau )\rangle }{{f_0}^2}\approx \frac{aN}{\sqrt{2\pi }}{\left(\frac{m}{2M}\right)}^2\frac{1}{\sqrt{1-\tau /{\tau }_D}}$$ (1)

with τ_D = L²/(2a²D) being the characteristic diffusion time, a = 4.42844 is a constant determined by the shape of the fundamental mode of the device, and M is the device’s total mass. The associated spectral density of fractional frequency fluctuation is

$$S_y(\omega )=\frac{aN}{\sqrt{2\pi }}{\left(\frac{m}{M}\right)}^2{\int }_0^{\infty }\frac{\text{cos}(\omega \tau )}{\sqrt{1+\tau /{\tau }_D}}d\tau =\frac{aN}{2}{\left(\frac{m}{M}\right)}^2·[{\tau }_d·\xi (\omega {\tau }_D)]$$ (2)

with ξ(x) ≡ g(√x)/√x, and g(√x) = cos(x) + sin(x) − 2C₁(√x)cos(x) − 2S₁(√ x)sin(x), where C₁(x) and S₁(x) are the Fresnel integrals³⁰ (see details in Supporting Information), and ω = 2πf is the Fourier (offset) frequency.

The measured noise spectra of fractional frequency fluctuations (Figure 4a) clearly demonstrate that there is excess noise due to surface Xe adsorbates. In the case of no e, the spectrum exhibits 1/f oise at very low offset frequency (~0.1–2 Hz) and flattens out above 2 Hz, indicating the instrumentation noise floor of the system. Figure 4b shows the adsorbate-induced excess noise spectrum, S_y,Xe(ω) = S_y,total(ω) − S_y,noXe(ω), extracted from such measurements performed at four different temperatures in the range of interest. We compute the diffusion time τ_D by numerically fitting the measured spectral density data to eq 2, as shown in Figure 4c. The measurement and analysis yield τ_D ~ 0.05–0.11s, and we obtain the corresponding diffusion coefficient D = L²/(2a²τ_D) to be in the range of D ~ 1.2–2.5 × 10⁻⁸cm²/s (we note this is at the same level as reported for Xe diffusion on some other surfaces²⁵). In Figure 4a and b, on the right axis we also show the corresponding adsorbed Xe mass fluctuation noise $S_{\mathrm{m}}^{1/2}(\omega )=f_0{S}_{\mathrm{y}}^{1/2}(\omega )/ℛ$ set by the measured fractional frequency noise.

On the basis of the measured diffusion noise spectra, we estimate the excess Allan deviation due to diffusion, by integrating the fitted noise spectral density (see Supporting Information).³¹ In our experimental regime (τ_A ≫ τ_D), we have σ_A,diff(τ_A) ≈ 0.83·√N (m/M)(τ_D/τ_A)^1/4, and the total expected instability due to adsorbate diffusion is thus ${\sigma }_{\mathrm{A},\text{diff},\text{total}}={({\sigma }_{\mathrm{A},\text{sys}}^2+{\sigma }_{\mathrm{A},\text{diff}}^2)}^{1/2}$. As Figure 3 demonstrates, this model yields excellent agreement in both the temperature dependency and the magnitude of the experimental data. Contrasted with the predictions of the pure adsorption–desorption model, this provides strong support for a surface kinetics dominated by surface diffusion. Very interestingly and importantly, the combined measurements and analyses have revealed a noise process that has new power laws S_y(ω) ~ ω^α with α = −1/2 and instability σ_A(τ_A) ~ τ_A^β with β = −1/4, which to the best of our knowledge have never been documented nor considered in conventional oscillators and clocks (i.e., all known oscillator noise spectra power laws involve an integer exponent α=0, ±1, ±2…).³² The revelation of these new weak power laws is possible because for the first time we are now able to tune a very sensitive VHF NEMS resonator to follow in real time the one-dimensional diffusion of adsorbate. It is important to point out the general character of our diffusion noise analysis, which could straightforwardly be extended by means of numerical simulations to account for the properties of different adsorption sites and/or different coverage regimes.

In conclusion, we have investigated the kinetics and fluctuations of surface adsorbate on a high-Q NEMS resonator vibrating at 190.5 MHz. By measuring and analyzing the temperature-programmed adsorption spectrum and device frequency fluctuations, we have found that adsorbate diffusion can dominate the observed excess noise. The sensitive measurements have also led to the discovery of new power laws of frequency noise in low-dimensional systems. These first measurements of surface adsorbates dynamics and fluctuations using resonant NEMS may have important implications for at least the following fundamental and technological applications: (i) The surface adsorbates-induced noise translates into equivalent mass fluctuations on the device surface; this imposes limits for the achievable sensitivity of frequency-shift based sensors. (ii) Following this study, it has been attempted to control and engineer adsorbates distribution (e.g., concentration gradient) and surface kinetics to enhance NEMS sensors’ functions and performance.³³ (iii) The approach of using NEMS to probe submonolayer surface physics may prove to be a useful supplement to the existing surface science tools, particularly when combined with in situ techniques,³⁴ to pursue, for example, quantitative, real-time measurements of mesoscopic processes such as interfacial damping and atomic tribology.³⁵ Further engineering with innovative device geometries and resonant mode shapes can also help to explore nanoscale Chladni figures³⁶ that may be important for molecular-scale biodetection in fluids and other complicated surface phenomena. This study also opens new opportunities for pushing the limits by investigating surfaces of NEMS made of other emerging materials such as ultrathin nanowires,³⁷ nanotubes,³⁸ and atomically thin graphene sheets.³⁹

Figure 1.

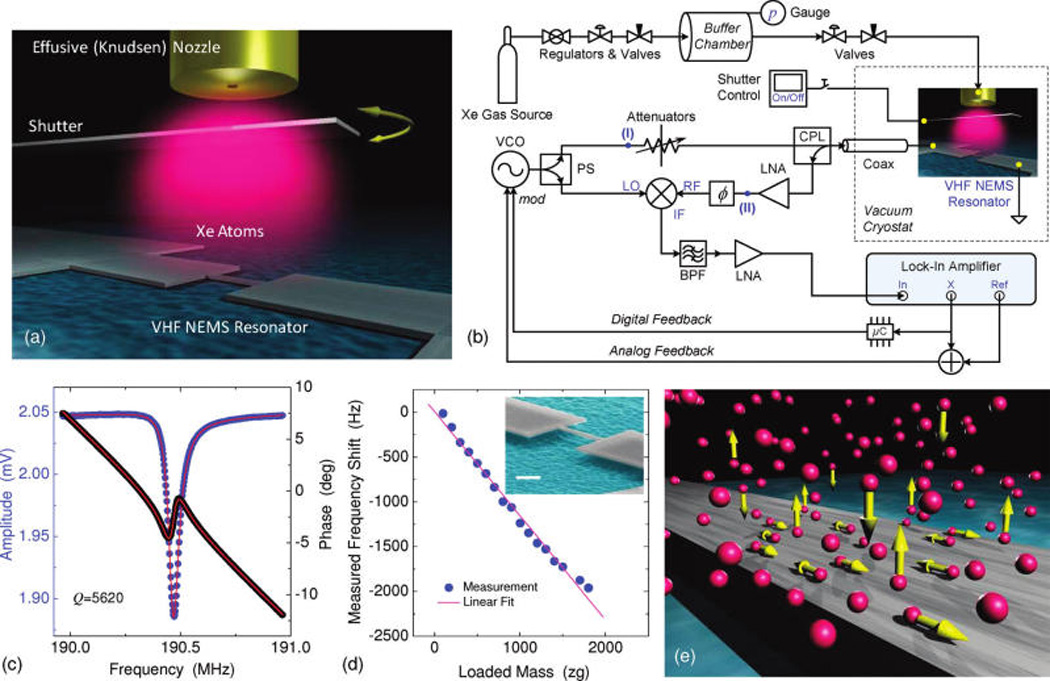
Adsorbates fluctuations on the surface of a VHF nanoelectromechanical resonator. (a) Illustration of an effusive atomic beam delivering a minute amount of Xe atoms onto the surface of a cold NEMS resonator. (b) Experimental system diagram and schematic of measurement circuits (with acronyms as detailed in Supporting Information). Shown is the closed-loop case; in case of open loop NEMS resonance detection, a network analyzer is connected between nodes (I) and (II). (c) Resonance response near f₀ = 190.5 MHz measured via reflectometric network analysis using magnetomotive transduction. The fit (red lines) gives a quality factor Q≈5620. (d) Calibrated mass responsivity of the device, ℛ ≡ |∂f₀/∂M| = 0.99 Hz/zg, measured in continuous mass-loading mode. Inset: scanning electron microscope (SEM) image of the VHF NEMS resonator; scale bar is 1 µm. (e) Illustration of Xe atoms-NEMS interactions with atoms kinetics including adsorption–desorption (out-of-plane) and surface diffusion (in-plane).

Figure 2.

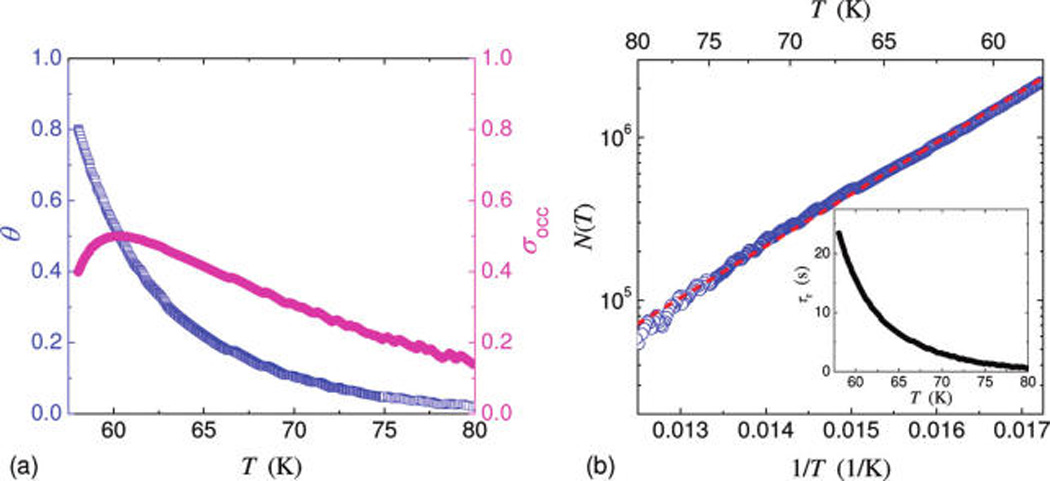
Surface kinetics of adsorbed Xe atoms on the NEMS device via resonant measurements. (a) Measured effective surface coverage (θ, left axis), along with the calculated surface occupation deviation (σ_occ, right axis) based on measurement data. (b) Measured number of adsorbed atoms (data: blue circles) and the fit to the Arrhenius equation (dashed line). The fit yields E_a ≈ 63.1 ± 0.23 meV, and v_a ≈ (1.23 ± 0.05) × 10⁴ Hz. Inset: the characteristic correlation time assuming a pure adsorption–desorption process, τ_r = 1/(r_ad + r_des) = N/(sIA_D).

Figure 3.

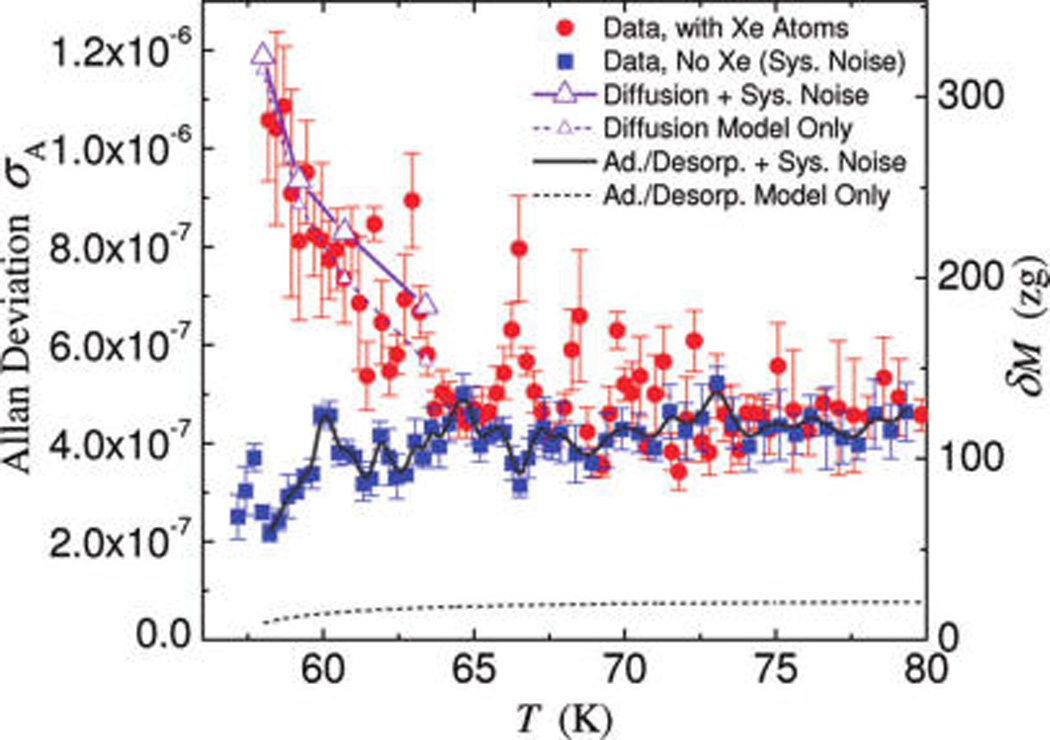
Frequency instability induced by surface adsorbate fluctuations. Red circles are the measured Allan deviation in the case of constant flux of impinging Xe atoms and blue squares in the case of no Xe flux (system noise floor). In the range of T ≈ 58–80 K, the excess frequency fluctuation due to adsorbed Xe atoms is clearly visible. The dashed lines are excess Allan deviation due to diffusion (violet with small triangles, see entries in Table 1, last column) and pure adsorption–desorption (dark gray), respectively. The solid lines are total instability levels calculated by adding in quadrature the system instability to that due to diffusion (violet with large triangles) and adsorption–desorption (dark gray), respectively. Allan deviation is measured with an averaging time τ_A = 1 s to ensure adequately dense data with respect to the regulated temperature change. Data symbols are average values and error bars are standard deviations, each computed from ensembles of 500 raw data points.

Figure 4.

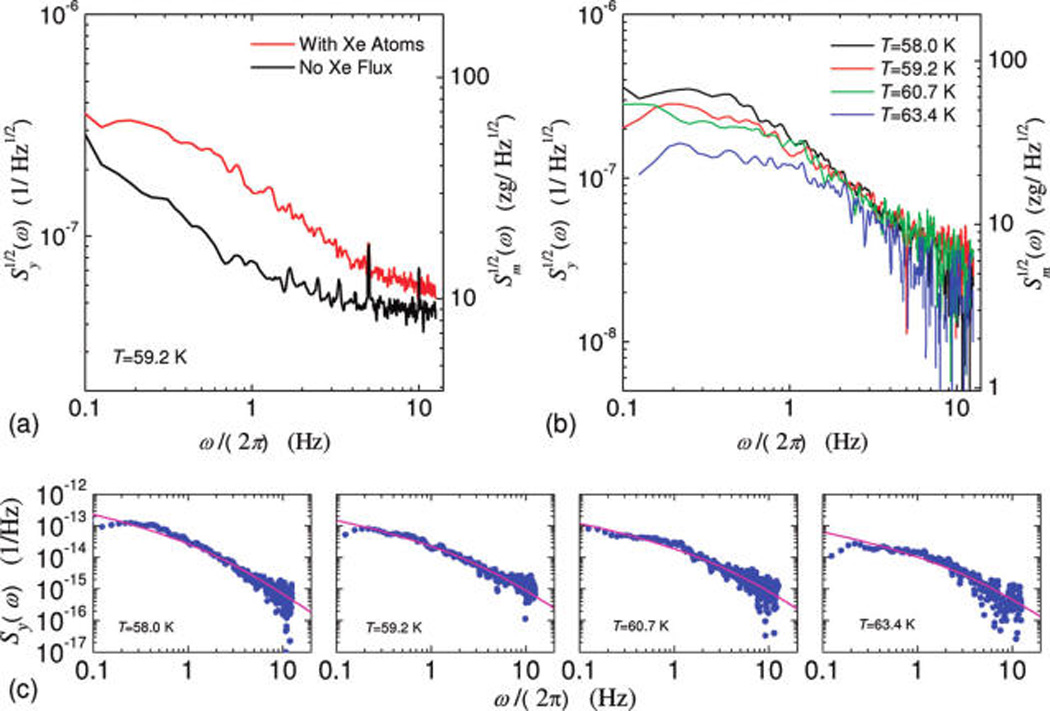
Noise spectra of VHF NEMS resonator due to adsorbed Xe atoms. (a) Measured noise spectral density of fractional frequency fluctuation at T = 59.2 K with and without Xe atoms. (b) Excess noise spectral density of fractional frequency fluctuations due to Xe adsorbates, measured at four different temperatures. (c) Least-squares fit of the measured excess noise spectral density data to the predicted function based on the diffusion noise model (see Supporting Information) to extract diffusion time constants and coefficients at various temperatures (results collected in Table 1).

Table 1.

Diffusion Time Constants and Coefficients^a

T (K)	N (T)	τD (s)	D (cm2/s)	σA,diff (τA = 1s)
58.0	2.19 × 106	0.114	1.18 × 10−8	1.16 × 10−6
59.2	1.71 × 106	0.064	2.12 × 10−8	8.86 × 10−7
60.7	1.27 × 106	0.055	2.44 × 10−8	7.36 × 10−7
63.4	7.69 × 105	0.053	2.53 × 10−8	5.69 × 10−7

^aData derived from the combined analysis in Figure 4 (diffusion noise model) and Figure 2 (loading curve).