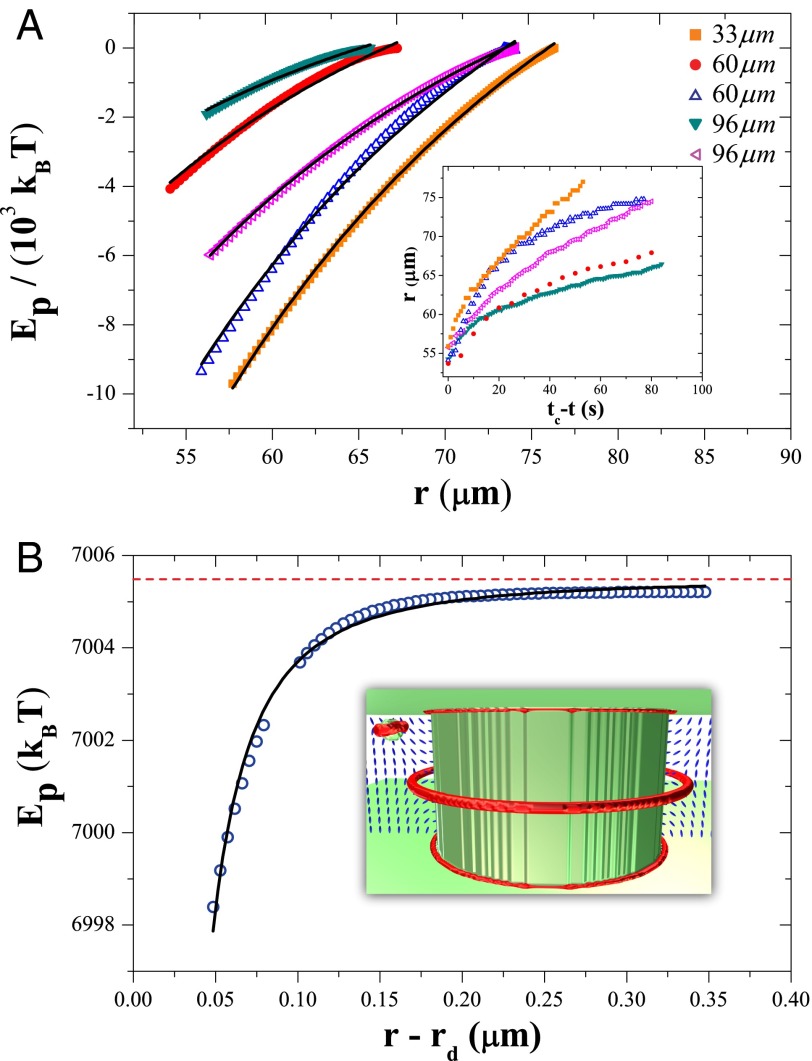
Fig. 5.

Elastic potential. (A) Migration of colloids implies bulk–colloid interaction energies on the order of 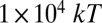and follows 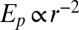(solid curves), where 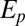is the inferred elastic potential and r is the radial distance in the horizontal plane from the center of the micropost. As the height of a micropost is increased (different curves), attractions become weaker due to an increased separation between particles and the bulk defect. (Inset) Migration rates are faster for microposts with base curvature compared with those of comparable height that have a sharp corner at the base (corner Y in Fig. 2A). This is due to the tendency of the bulk disclination to position itself closer to the free interface for microposts with curved bases. Closed symbols indicate microposts with a curved base. (B) Numerically modeled energy of a colloidal sphere approaching a micropost capturing the 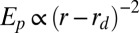dependence of the quadrupolar colloid interacting with a disclination ring. The red dashed line represents the asymptotic value for 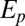at large distances, and 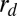is the radius of the micropost’s disclination ring. (Inset) Representative image of the numerical modeling.