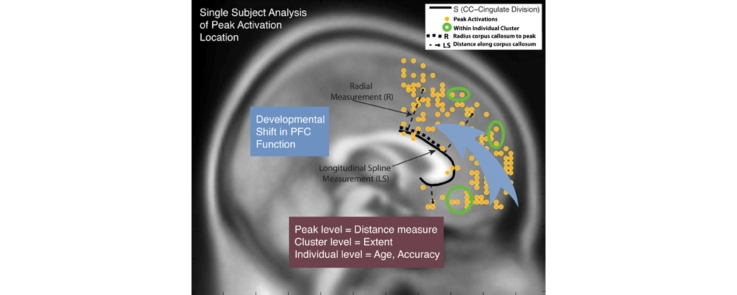
Graphical abstract
Abbreviations: MFC, medial frontal cortex; FC, frontal cortex; MSIT, Multisource Interference Task; RT, reaction time; LS, longitudinal spline; R, radius
Keywords: Single subject activation, fMRI, Human development, Cognitive control, Hierarchical linear modeling
Highlights
-
•
Single subject topographical analysis of interference and error in children and adults.
-
•
Individual activation locations measured by distance along the corpus callosum.
-
•
Hierarchical linear modeling analysis controlling for nested nature of data.
-
•
Age and accuracy related changes in MFC location during interference.
Abstract
Age-related improvements in human performance monitoring have been linked to maturation of medial frontal cortex (MFC) in healthy youth, however, imaging studies conflict regarding age-related changes in MFC activation patterns. Topographical analysis of single-subject activation enables measurement of variation in location of MFC activation by age, as well as other potentially influential factors (e.g., performance on task). In this study, 22 youth (ages 8–17 years) and 21 adults (ages 23–51 years) underwent functional magnetic resonance imaging during a performance monitoring task examining interference and errors. Single-subject factors (extent of MFC activation, age and accuracy) were entered into a three-level hierarchical linear model to test the influence of these characteristics on location of MFC activation. Activation shifted from a rostral/anterior to a more dorsal/posterior location with increasing age and accuracy during interference. Inclusion of age and accuracy accounted for almost all of the unexplained variance in location of interference-related activation within MFC. This pattern links improvement of performance-monitoring capacity to age-related increases in posterior MFC and decreases in anterior MFC activation. Taken together, these results show the maturation of performance monitoring capacity to depend on more focal engagement of posterior MFC substrate for cognitive control.
1. Introduction
Behavioral capacity to monitor performance develops throughout childhood and into adulthood; including the ability to ignore distractors, identify correct response and correct performance after a mistake (Casey et al., 2010). The medial frontal cortex (MFC) plays a key role in performance monitoring (Ridderinkhof et al., 2004), and the maturation of this region is linked to age-related improvement in performance monitoring capabilities (Fitzgerald et al., 2010). However, the way in which MFC maturation contributes to the development of performance monitoring remains an open question. Development contributes to changes in white matter and gray matter development and contributes to changes in the degree of specialized in function within an area, the location of specific brain functions, and connectivity to other areas to support behavioral performance (Johnson, 2011). Within the MFC the literature is conflicting on whether MFC activation becomes more focal with development, whether shifts in MFC activation correlate with developmental performance improvements and whether the location of performance monitoring shifts within the MFC during development.
Performance monitoring has been associated with conflicting reports of age-related decreases (Durston et al., 2006, Marsh et al., 2006, Velanova et al., 2008) and increases (Adleman et al., 2002, Schroeter et al., 2004, Rubia et al., 2007, Fitzgerald et al., 2010) in magnitude of MFC activity. In addition, some work suggests that the extent of activation (measured by the number of voxels activated) becomes more focal (Schroeter et al., 2004, Durston et al., 2006, Lamm et al., 2006, Velanova et al., 2009) or broader with age (Adleman et al., 2002, Bunge et al., 2002). Cognitive developmental theories of interactive specialization identify the PFC as a region that is less specialized in childhood and becomes more specialized during development. Theoretically children should exhibit a more diffuse activation during than adults with a greater specialization with age (Johnson, 2011). Developmental differences in magnitude and extent of activation can be confounded by traditional group-averaged data, which may contribute to the instability of MFC findings across developmental studies. Specifically, group differences may either be minimized or spuriously introduced by individual subjects in whom magnitude and/or extent of activation in a particular location differs substantially from the group average (Stern et al., 2009). Large variance in the location of individual peaks of activation may reduce the power to identify group differences in averaged data. Individual peak activity may vary across a range of 8–10 cm activation within the medial frontal wall (Taylor et al., 2006). In addition, individual variability in performance may obscure developmental change in extent of PFC activation.
There are likely developmental differences in how the brain responds to the demands of performance monitoring tasks as performance improves with age. One study demonstrated an increase in dorsal/posterior MFC and a decrease in an anterior/rostral region with age while controlling for performance (Perlman and Pelphrey, 2010). However they also found the reverse pattern correlated with higher levels of fearful temperament. This may suggest that while children are performing a task at similar levels, some may view the task as more emotionally salient. Prior work has established that ventral regions of the MFC are activated in response to more emotionally salient information (Somerville and Casey, 2010). Emotional salience of cognitive tasks may change with age as well. Children may struggle more to maintain performance on a task with greater emotional arousal.
Age-related changes in location of aspects of performance monitoring function within MFC have not been well studied. However, given the role of dorsal MFC in successful performance monitoring (Ridderinkof et al., 2004), age-related increases in dorsal MFC activation should correspond with maturation of performance monitoring function. Other work differentiates between the use of rostral MFC for new rule learning and premotor dorsal FC for simple action rules (Badre and D’Esposito, 2009). There may be a developmental shift where children utilize new rule learning neuroanatomical regions (rostral MFC) to maintain the same level of performance on tasks that would be processed as simple action rules by adults (premotor dorsal FC). Better performing adults and children (i.e., those with well learned rule execution) should process in dorsal/posterior MFC during on low load tasks. However, as children develop, performance (i.e., accuracy) generally improves, necessitating the consideration of performance measures, as well as age, in mapping the development of performance monitoring function (Casey et al., 2008).
The present study seeks to examine the development of performance monitoring in children and adults ages 8–51. By analyzing topographical measures of MFC location (Stern et al., 2009). We sought to gain insight into the development of MFC-based performance monitoring function by analyzing single subject activation during the Multisource Interference Task (MSIT; Bush et al., 2003). The MSIT requires participants to respond to the different number out of three numbers presented onscreen. There are two conditions, congruent, in which the target number is flanked by Xs and incongruent where the target number is flanked by distracting numbers. Hierarchical linear modeling enabled us to examine the independent role of age, accuracy and activation extent on location of peak activations within the MFC. Based on work indicating a shift in location of activation from new rule learning to simple action rules, we hypothesized that better performance would predict a shift in location of activation from rostral/anterior to dorsal/posterior MFC independent of age. In addition, we hypothesized that the similar shift would be exhibited based on age, independent of performance. This hypothesis was based on prior work showing a dorsal developmental shift in function. Finally, based on the interactive specialization theory of developmental cognitive neuroscience, we predicted age and accuracy would associate with a shift from more diffuse MFC activation extent to more focal extent of activation within posterior MFC.
2. Materials and methods
Permission to conduct this study was obtained through the University of Michigan Institutional Review Board and the research conforms to the Code of Ethics of the World Medical Association (Declaration of Helsinki). According the IRB procedures, consent was obtained by adults and parents of children and children provide assent to participate in this study.
2.1. Participants
Healthy youth and adults were recruited through community advertisements, flyers and a university sponsored research recruitment website. Twenty-nine healthy children and adolescents between the ages of 8–17 (16 females; mean age = 12.9, SD = 2.8) and 21 healthy adults between ages 23–51 (6 females; mean age = 39.8, SD = 9.4) were recruited. Data from seven children were excluded (failure to understand task, n = 1; image quality, n = 3; excessive movement, n = 3, movement greater than 2 mm or degrees for one or more brain volumes) for use in data analysis, resulting in a final group of 22 children. Participants were first prescreened during an initial phone interview to ensure no history of serious medical or neurological illness, head trauma, or mental retardation. Youth who were eligible after phone pre-screening were interviewed to ensure no current or prior history of psychiatric illness using the Kiddie-Schedule for Affective Disorders – Present and Lifetime Version (Kaufman et al., 1997) or the Structured Clinical Interview for Diagnosis (First et al., 1996), as appropriate to age group. [For greater detail on selection criteria and methods, the reader is referred to Fitzgerald et al. (2010)].
2.2. Task
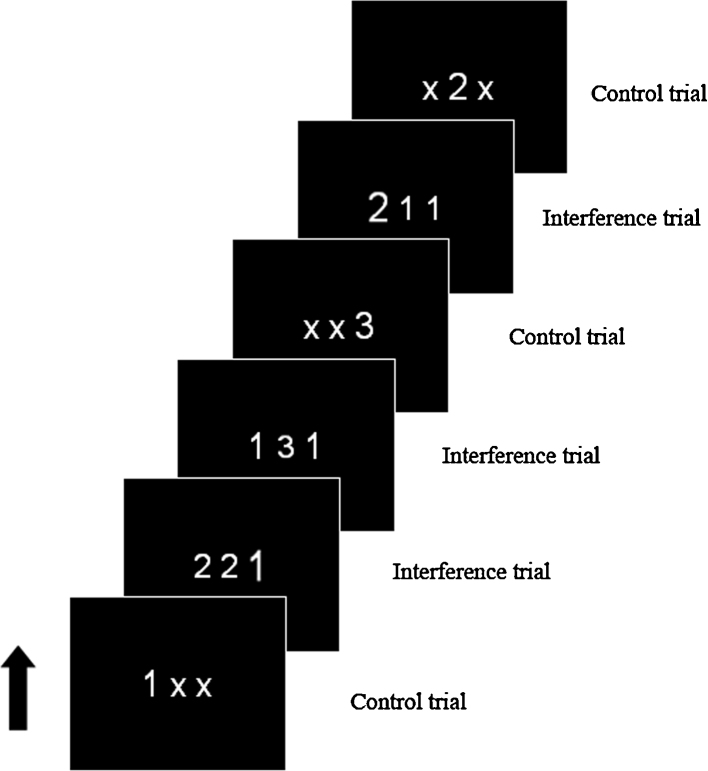
Participants performed a modified version of the Multisource Interference Task (MSIT), a cognitive interference task that elicits a robust interference signal in the medial prefrontal cortex (MFC) at the single-subject level (Bush et al., 2003). Participants were presented with three numbers printed in white on a black background and instructed to press a button indicating the identity of the “oddball” number. Oddball refers to the case that is different when others are the same. In this case participants are presented with three numerals side by side, two are the same and one is different. They are instructed to pick out the different number. Participants pressed the 1st, 2nd or 3rd button to indicate the numbers 1, 2 and 3, respectively. In control trials, the target number was flanked by the letter “x” and was in the same position as the correct button response (e.g., number 2 was in the second position). In interference trials, competing but incorrect numbers flanked the target number and the position of the target number did not correspond with the correct button response (e.g., the oddball number is “1” but it is in the 3rd position). On half of the trials the font size of the target number was larger than distracters and in the other half of the trials the font size of the target was smaller (see Fig. 1).
Fig. 1.
Multisource Interference Task (MSIT) paradigm.
The original block design of the MSIT was modified for an event-related presentation to enable the separation of correct from error trials. Participants completed 5 runs with 60 trials per run for a total of 300 trials. The experiment consisted of 60 fixation trials (white + on black background), 120 interference trials, and 120 control trials, presented in a pseudorandom order. Stimuli appeared for 500 ms and followed by a 2500 ms inter-stimulus interval (ISI, white + on black background).
2.3. Data analysis
2.3.1. Behavioral analysis
Reaction time and accuracy data were collected during scanning on a trial-by-trial basis. Accuracy and difference between incongruent and congruent conditions in reaction time (RT) and accuracy were submitted to ANCOVA with age as a covariate.
2.3.2. Data acquisition and preprocessing
Scanning took place on a 3.0 T GE Signa scanner (LX [8.3] release, Neuro-optimized gradients), beginning with the acquisition of a standard, axial T1-image for anatomic normalization and alignment (gradient-recall-echo, repetition-time TR = 2000 ms, echo-time TE = 30 ms, flip-angle FA = 90, field-of-view FOV = 20 cm, 40 slices, slice-thickness = 3.0 mm, 64 × 64 matrix). Next, a reverse-spiral acquisition sequence was applied to collect T2* weighted images in the same prescription as the T1-image, with 85 volumes per session. This protocol has been shown to minimize magnetic susceptibility to enable signal recovery in regions of the brain that lie near air/tissue boundaries (Stenger et al., 2002, Yang et al., 2002). After the functional volumes were acquired, a high resolution T1 scan (3D SPGR, TR = 10.5 ms, TE = 3.4 ms, FA = 25, FOV = 24 cm, 102 slices, slice thickness = 1.5 mm, 256 × 256 matrix) was obtained for anatomic normalization. Subject head movement was minimized through instructions to the participant and packing with foam padding that we have found to be well tolerated by children. Data underwent standard preprocessing steps including slice-timing correction, realignment of functional data (mcflirt, http://www.fmrib.ox.ac.uk/fsl/) and thresholding to exclude non-brain voxels from subsequent analysis. Functional volumes were normalized to the MNI152 template of the SPM2 software package, an average of 152 T1 images from the Montreal Neurological Institute. Data were then resliced and smoothed with a 5 mm isotropic Gaussian smoothing kernel (voxel size after preprocessing was 3 mm × 3 mm × 3 mm).
2.3.3. Functional imaging analyses
Functional data were analyzed using a standard random effects analysis within the framework of the modified General Linear Model (Worsley and Friston, 1995, Worsley et al., 2002), implemented using SPM2. Three conditions were modeled (errors, correct interference trials, and correct control trials) to enable the calculation of contrasts of interest for errors (all errors – all correct) and for interference (interference trials – control trials) for each subject. Errors and interference processing were both assessed given prior work suggesting these functions may be distinct elements of performance monitoring that engage more dorsal, and more rostral aspects of the MFC, respectively (Ridderinkhof, 2004, Hester et al., 2008). Previous research has found robust signal of error-related brain activation with three or more error trials (Stern et al., 2009). Thus, six adults and 2 youth who committed less than three errors were excluded from this analysis, leaving 20 youth and 15 adults with sufficient errors for inclusion in the error analysis. Single-subject contrasts were carried forward into hierarchical linear modeling (HLM) to test the relationship of topographical measures of MFC activation with individual characteristics of age and performance.
2.3.4. Group analyses
Whole-brain group analyses of both interference (incongruent – congruent) and error (error – correct) contrasts were previously reported (Fitzgerald et al., 2010) and showed robust MFC activation for youth and adult groups when examined separately, but no differences between groups.
2.3.5. Topographic analyses of MFC activation
Previously our lab has defined a procedure for the measurement of the locations of individual activations in the MFC (see Stern et al., 2009). In brief, a large MFC search volume was specified (coordinate bounds: x = +18 to −18, y = 1 to 71, z = −18 to 72). Since the analysis focused on differential spatial distribution of peaks, rather than the significance of individual peaks, a liberal threshold of p < 0.005 uncorrected and an extent ≥10 voxels (volume of 270 mm3) was used to threshold single-subject activation maps. Within the confines of this space, individual interference and error contrasts were examined to characterize MFC activations for each subject based on (1) location (i.e., peak coordinates) and (2) extent of cluster associated with each peak. Similar numbers of youth and adults activated the MFC for both the interference (12/22 youth and 13/21 adults) and error contrasts (16/19 youth and 11/15 adults).
We defined two measurements to characterize the location of each peak activation (Stern et al., 2009). A two-dimensional cubic spline (S) was fit to a series of points located along the border of the corpus callosum (Steele and Lawrie, 2004) of the MNI152 brain. A point P along the spline S was determined for each peak of each cluster or sub-cluster, projected across the lateral dimension (x = −18 to +18), enabling the calculation of two indices of spatial location (see Fig. 2, Fig. 3). First, the radial measurement (R) from point P to each cluster peak was calculated. Second, the distance along line S (starting at y = 0) from point P – the longitudinal spline (LS) – was measured. Radial measurements were along the dorsal–ventral dimension and longitudinal spline measurements generally gave the distribution of clusters in the anterior–posterior dimension. For clusters located subgenually, a longer longitudinal spline measurement would have been recorded, following the neuroanatomy of the corpus callosum (Stern et al., 2009, Steele and Lawrie, 2004). Radial and longitudinal spline measurements were computed for the maximal peak and sub-peaks within each cluster of activation. In addition, the extent of activation for each cluster was calculated based on total number of voxels per cluster. Scatterplot age and distance were examined with linear, quadratic and cubic linear estimates. There was no evidence of a quadratic or cubic relation between age and radius or longitudinal spline.
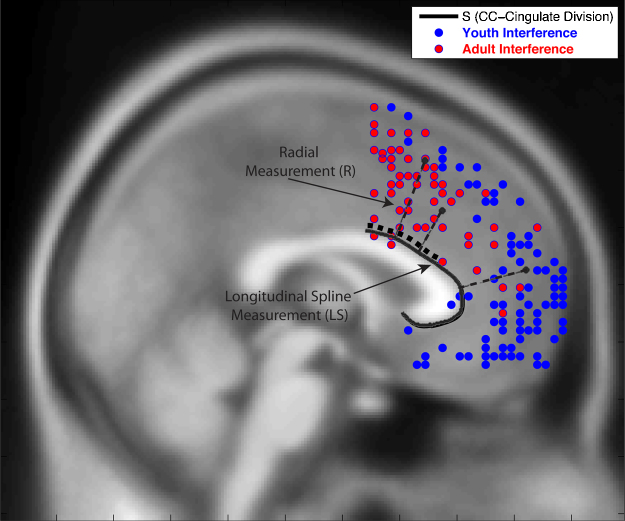
Fig. 2.
Youth and Adult Topographical Map of Locations of peak activations during interference within coordinate bounds: x = +18 to −18, y = 1 to 71, z = −18 to 72. Individual subjects can contribute multiple peaks.
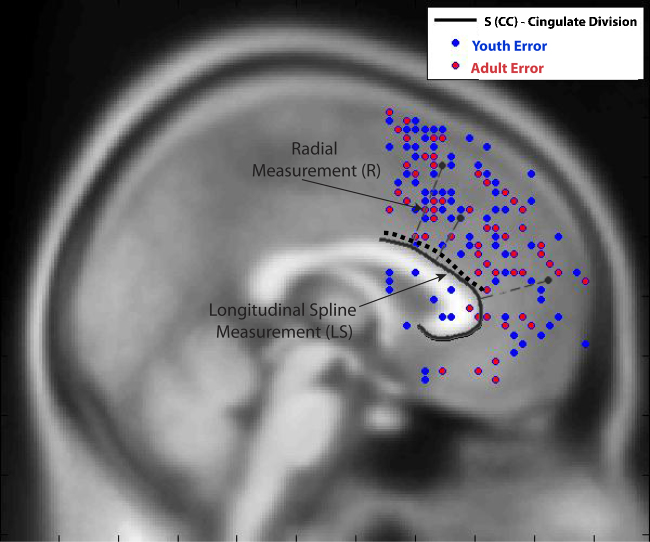
Fig. 3.
Youth and Adult Topographical Map of Locations of peak activations during error commission within coordinate bounds: x = +18 to −18, y = 1 to 71, z = −18 to 72. Individual subjects can contribute multiple peaks.
For the primary analyses of interest, we fitted three-level hierarchical linear models (HLMs) (Raudenbush and Bryk, 2002) using the HLM 6.0 software (Raudenbush and Bryk, 2004). In each of these models, locations of peaks and sub-peaks on radial and longitudinal splines defined the first level of measurement (Level 1), and these were the dependent variables of interest. The location measures were nested within clusters of activation, which often included a maximal peak and multiple sub-peaks (Level 2) that in turn were nested within individuals (Level 3). We estimated the fixed effects of cluster extent (a level-two covariate), subject age (a level-three, or individual-level, covariate), and subject accuracy (also a level-three covariate) on the locations of the peaks. The models also included random effects for clusters nested within individuals, and random effects for individuals (allowing for correlations of Leve1 1 location measures within clusters and individuals). Analyses were conducted separately for peak locations based on radius (R) and longitudinal spline (LS), for both error and interference contrasts, yielding four different HLMs (see Table 1).
Table 1.
Hierarchical linear model equations, variables and summary of results.
| Level of analysis | Equation | Dependent variable | Independent variables | Result |
|---|---|---|---|---|
| Interference longitudinal spline (LS) final model | ||||
| Level 1 | Y = P0 + E | LS distance along CC | Mean LS + error variance | Mean LS = 28.24 mm |
| Level 2 | P0 = B00 + B01*(CLUSTER) + R0 | LS distance along CC | Cluster extent + error variance | N.S. |
| Level 3 | B00 = G000 + G001(EXACT AG) + G002(INC_ACC) + U00 | LS distance along CC | Age + accuracy + error variance | MFC activation moved posteriorly along the corpus callosum by:
• 0.79 mm per year older • 0.43 mm for each percentage point more accurate |
| B01 = G010 + G011(AGE) + G012(ACC) | Cluster extent | Age + accuracy | Age and accuracy interacted with cluster extent to predict LS (Fig. 3) | |
| Explained variance | Level 1 variance − Level 3 variance/Level 1 variance | Difference between unconditional model and three level model | 85% of total variance in peak locations was due to individual factors | |
| Interference radius (R) final model | ||||
| Level 1 | Y = P0 + E | Radial measure from CC to peak | Mean R + error variance | Mean R = 22.63 mm (22.93 mm in unconditional model) |
| Level 2 | P0 = B00 + B01*(CLUSTER) + R0 | Radial measure from CC to peak | Cluster extent + error variance | N.S. |
| Level 3 | B00 = G000 + G001(EXACT_AG) + G002(INC_ACC) + U00 | Radial measure from CC to peak | Age + accuracy + error variance | N.S. |
| B01 = G010 + G011(AGE) + G012(ACC) | Cluster extent | Age + accuracy | N.S. | |
| Explained variance | Level 3 variance/total variance | Percent of variance | 10% of total variance accounted for by age and accuracy | |
| Error longitudinal spline (LS) final model | ||||
| Level 1 | Y = P0 + E | LS distance along CC | Mean LS + error variance | Mean LS = 26.01 mm |
| Level 2 | P0 = B00 + B01*(CLUSTER) + R0 | LS distance along CC | Cluster extent + error variance | N.S. |
| Level 3 | B00 = G000 + G001(EXACT_AG) + G002(INC_ACC) + U00 | LS Distance along CC | Age + total errors + error variance | MFC activation moved anteriorly along the corpus callosum by:
• 0.30 mm per error • 0.04 mm |
| B01 = G010 + G011(AGE) + G012(ACC) | Cluster extent | Age + total errors | Age interacted with cluster extent to predict LS (Fig. 4) | |
| Explained variance | Unconditional Level 3 variance − final Level 3 variance/unconditional Level 3 variance | Proportion of individual variance explained | 96% of total individual variance was explained by age and total number of errors | |
| Error radius (R) final model | ||||
| Level 1 | Y = P0 + E | Radial measure from CC to peak | Mean R + error variance | Mean R = 21.98 mm (22.18 mm in unconditional model) |
| Level 2 | P0 = B00 + B01*(CLUSTER) + R0 | Radial measure from CC to peak | Cluster extent + error variance | N.S. |
| Level 3 | B00 = G000 + G001(EXACT_AG) + G002(INC_ACC) + U00 | Radial measure from CC to peak | Age + total errors + error variance | MFC activation moved posteriorly along the corpus callosum by:
• 0.21 mm per year older |
| B01 = G010 + G011(AGE) + G012(ACC) | Cluster extent | Age + total errors | Age and Accuracy interacted with cluster extent to predict R (Fig. 5) | |
| Explained variance | Unconditional Level 2 variance − final Level 2 variance/unconditional Level 2 variance | Percent of variance | 18% of total cluster level variance accounted for by cluster extent | |
Prior to the selection of the final model two additional predictors were examined. First, to explore interdependence between our distance measures, we modeled each outcome measure (LS and R) with and without the other as a level one predictor; however, there was no evidence of interdependence. Second, we examined gender as a level three predictor however the inclusion of this variable was also insignificant. In order to proceed with the most parsimonious model the other distance measure and gender were eliminated as predictors.
Three different models were fitted for each of four dependent variables (LS and R, each for interference and error conditions). First, an unconditional three-level model was used to quantify the amount of unexplained variance in location across the three levels (Level 1: peak level, Level 2: cluster level and Level 3: individual level). Unconditional models are necessary to fit as a basis for quantifying the amount of unexplained variance at levels two and three of analysis that can be accounted for by the later conditional models (Raudenbush and Bryk, 2002).
Next, a full three-level model was examined. At the first level the peak location (the dependent variable, measured by either longitudinal spline or radius for each individual) was entered. At the cluster level of the model (Level 2), the extent of the cluster was entered as the only cluster-level covariate, expected to explain variance in peak locations. Finally, individual-level covariates entered at Level 3 of the model included the age of the participant (centered relative to the grand mean) and accuracy. In the Interference condition, the percent of accuracy during interference was used. For the error condition we used the total count of commission errors. The three-level HLM (full model) allowed us to (1) test for the linear effects of age and accuracy on the location of MFC activation (2) and control for the potential influence of difference in extent of clusters on peak location.
It is important to note that each individual could have multiple peaks corresponding to multiple clusters of MFC activation, and multiple sub-peaks within each cluster. This analysis partitions the total variance of location of MFC activations into between-person variance (based on age and accuracy), between-cluster variance (based on extent, i.e., the number of voxels per cluster within a subject), and between-location variance within a cluster (locations of cluster and sub-cluster peaks within a subject).
To account for the possible interactions between factors at different levels, at the third stage a final three-level model was examined. This final model included the predictors in the full model and allowed for a three-way interaction between age, accuracy, and cluster extent on location of activation. This was an exploratory analysis to understand if there was a change in the association between cluster extent and location based on age or accuracy. For simplicity of presentation, significant results are presented. Variables not discussed are non-significant predictors.
3. Results
3.1. Behavioral results
Results of ANCOVA in the full group of 43 subjects showed a linear effect of age where performance increased with age in both congruent, F(1,43) = 6.209, p < 0.05, and incongruent conditions, F(1,43) = 14.110, p = 0.001. There was also a linear effect of age on the difference in RT between congruent and incongruent conditions such that younger subjects had a greater difference in RT between tasks, F(1,43) = 4.084, p = 0.05.
3.2. Functional results
3.2.1. HLM of interference
3.2.1.1. Interference longitudinal spline
The unconditional means model for longitudinal spline (LS) showed significant unexplained individual-level variance in location of peaks along the LS (χ2(23) = 65.05, sd = 12.05, p < 0.001, see Fig. 2). In other words, on average, peaks occurred in different locations for different individuals (as expected). The estimated standard deviation of HLM random effects are assumed to arise from a normal distribution with mean 0 and some standard deviation. In addition, the mean locations of cluster peaks within individuals varied significantly (χ2(29) = 173.32, sd = 10.97, p < 0.001). The estimated mean location of peaks along the LS of the corpus callosum (β = 28.56, t = 8.99, p < 0.001) was 28.56 mm from the posterior edge of our LS measurement (i.e., y = 0). Examination of level-three variance components revealed that the proportion of total variance in peak locations due to individual factors was 43% (equation: Level 3 variance/(Level 1 variance + Level 2 variance + Level 3 variance)) or τβ/(σ2 + τπ + τβ).
In a full model including the fixed effects of age of individual, accuracy (percent accuracy during interference), and cluster extent there was no longer unexplained variability at the individual level in LS (χ2(21) = 24.79, sd = 3.43, p > 0.1). Specifically, variability in LS between individuals was predicted by age (β = −0.83, t = −7.13, p < 0.001) when controlling for differences in cluster extent such that, for each year older, MFC activation moved posteriorly along the corpus callosum by 0.83 mm. Accuracy also uniquely predicted the location of clusters along the LS (β = −0.33, t = −2.88, p < 0.05) when included with age, such that with each percentage point greater accuracy, the location of the activation moved posteriorly by 0.33 mm. Between-cluster variability within individuals remained after including the fixed effect of cluster extent in the model (χ2(28) = 164.51, sd = 9.33, p < 0.001), suggesting that other cluster-level factors may be introducing variance in locations among the clusters.
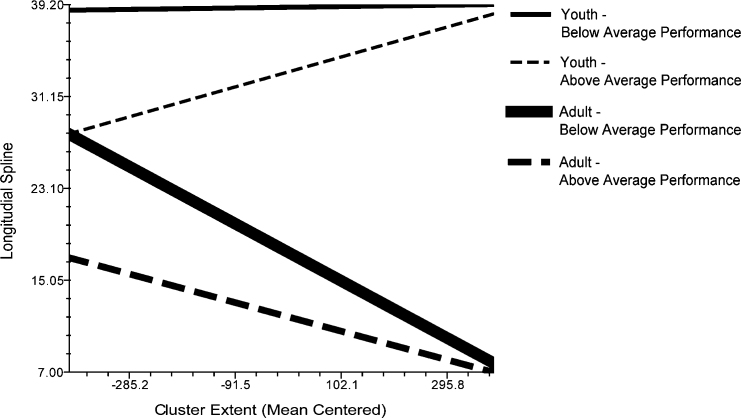
A final model allowing for a three-way interaction between age, accuracy and the extent of the cluster was fitted on the LS. In this model there remained no unexplained variability between individuals in LS location (χ2(21) = 31.07, sd = 4.65, p > 0.05). Age remained a predictor of LS when controlling for differences in cluster extent (β = −0.79, t = −5.66, p < 0.001), such that for each year older peak location was 0.79 mm more dorsal and posterior along the corpus callosum. Incongruent accuracy also significantly predicted location of clusters (β = −0.42, t = −2.72, p < 0.05), such that with each percentage point greater accuracy, activation was 0.42 mm more dorsal and posterior along the corpus callosum.
Incongruent accuracy interacted with the extent of cluster (β = 0.10, t = 2.45, p < 0.05), and there was also weak evidence of age interacting with extent of cluster (β = −0.001, t = −1.48, p < 0.1) to influence activation distance along the longitudinal spline. Interpreting these interactions, we found that with greater age and less accuracy, larger clusters were located closer to the y = 0 point, and with younger age and less accuracy, larger clusters were located farther away from the start of the y = 0 point (see Fig. 4). A comparison of the final three-level model to the unconditional model revealed that 85% of explainable individual-level variance in location of LS is explained by the inclusion of age and accuracy. There remained between-cluster variance within individuals in LS in this model.
Fig. 4.
Three way interaction of age, accuracy and cluster extent on distance along longitudinal spline during interference, illustrated with 25th and 75th percentile of age and performance.
3.2.1.2. Interference radial distance
The unconditional means model for radial distance (R) location had significant unexplained variance within individual (χ2(29) = 62.70, sd = 4.86, p = 0.001). There was no between individual differences in R (χ2(23) = 30.74, sd = 3.18, p > 0.1), with a mean R location of 22.93 mm from the corpus callosum. Examination of variance components indicated that only 10% at the level of individual factors, meaning that most of the variability in radial distance was within individuals, rather than between individuals. Within individual variability remained for the R distance in the full model (χ2(28) = 61.66, sd = 4.69, p = 0.001). None of the predictors significantly explained between within individual variability in R location.
3.2.2. HLM of error
3.2.2.1. Error longitudinal spline
The unconditional means model for LS during error found evidence of significant variance in location within individuals (χ2(61) = 552.78, sd = 17.29, p < 0.001, see Fig. 3), but not between individuals (χ2(26) = 23.55, sd = 3.77, p > 0.1). The mean location of LS from the y = 0 was 25.51 mm.
In a full model including cluster extent, age and accuracy (total commission errors), there remained significant cluster level unexplained variance within individual LS (χ2(60) = 501.42, sd = 16.75, p < 0.001). Differences in cluster extent (β = −0.04, t = −3.00, p < 0.005) predicted this within individual variance. In this full model, accuracy also predicted LS distance (β = −0.31, t = −2.20, p < 0.05) between individuals; however, age was not predictive (β = −0.10, t = −0.70, p > 0.1). Both greater cluster extent and more total commission errors were related to a shorter distance from the y = 0 point.
In a final model allowing for the interaction between Level 1 factors and Level 2 factors, there remained significant unexplained variance at the cluster level in LS measurement (χ2(60) = 449.01, sd = 16.59, p < 0.001), with the mean location of error activation ∼26 mm from the y = 0 point on the corpus callosum (β = 26.01 t = 13.78, p < 0.001). There remained a difference in LS based on accuracy (β = −0.31, t = −2.19, p < 0.05) and extent of clusters (β = −0.04, t = −4.85, p < 0.001) such that fewer error commissions, controlling for age and cluster extent were more rostral and anterior and larger clusters were located more dorsally and posteriorly.
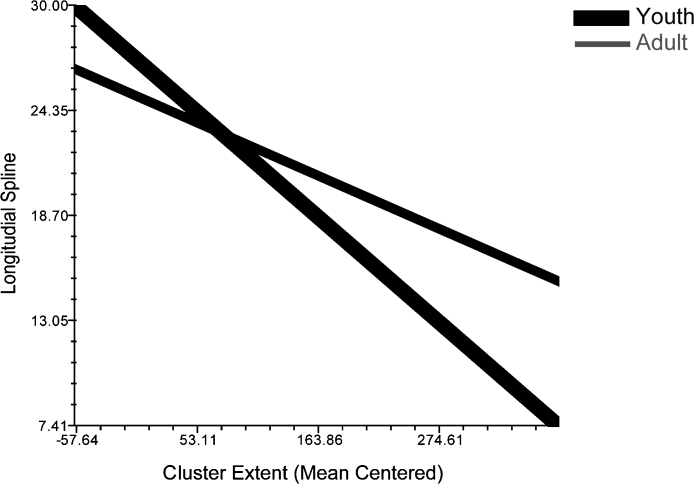
Individual age interacted with cluster extent (β = 0.001, t = 3.252, p < 0.005), such that smaller clusters in youth were located more rostrally and anteriorly and greater cluster extent was significantly closer to y = 0 in youth than in adults (see Fig. 5). Ninety-six percent of explainable variance in means between individuals was explained by the individual-level factors considered in this model.
Fig. 5.
Interaction of age and cluster extent on distance along longitudinal spline during error, illustrated with dichotomous grouping of data, illustrated with 25th and 75th percentile of age.
3.2.2.2. Error radial distance
There was also significant variability at within individuals in the unconditional means model of error R measurement (χ2(61) = 198.37, sd = 7.88, p < 0.001) and a trend level difference between individuals (χ2(26) = 37.32, sd = 3.98, p < 0.1) in error R. Average distance from the corpus callosum 22.18 mm. Examination of variance components revealed that only 11% of variance in R location of activations could be accounted for by the individual level.
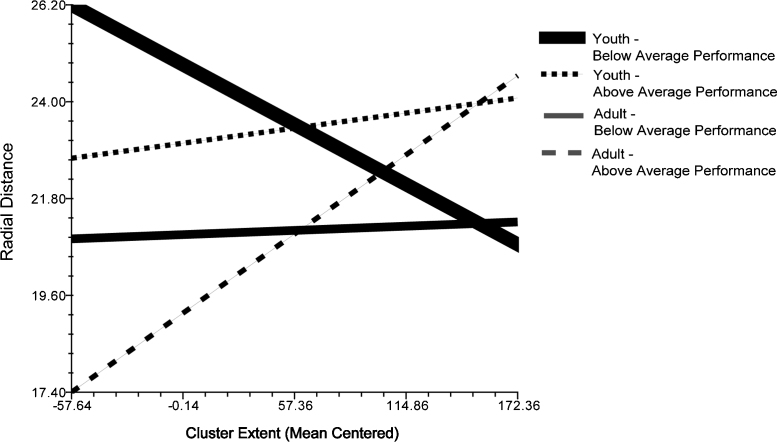
A full model with age, accuracy, and cluster extent revealed that age was a marginal predictor of R measurement (β = −0.18, t = −1.96, p < 0.1). The final model including interactions between individual level predictors and cluster extent revealed that age (β = 0.001, t = 2.51, p < 0.05) and accuracy (β = 0.001, t = 2.28, p < 0.05) interacted with cluster extent, such that older participants with more errors and large cluster extents activated further away from the corpus callosum, whereas for younger participants greater accuracy resulted in smaller and closer activation (see Fig. 6). In the final model 18% of the explainable cluster-level variance in activation location was explained by cluster extent.
Fig. 6.
Three way interaction of age, accuracy and cluster extent on radial distance during error processing, illustrated with 25th and 75th percentile of age and performance.
4. Discussion
We undertook a re-analysis of previously published data to demonstrate age-related differences in the location of MFC activity during a performance monitoring task using a topographic analysis. Our previous analysis with voxel-wise group contrasts found age-related increases in activation within a dorsal MFC ROI among youth, but failed to show magnitude or extent differences in MFC activation between youth and adults (see Fitzgerald et al., 2010). Because that analysis examined group-averaged data, it was unable to test age-related changes in location of MFC activation. In this re-analysis, topographic distribution of individual activations was assessed across the wall of the MFC, demonstrating that activation during interference processing shifted from a rostral/anterior MFC to dorsal/posterior with age. In addition, better performance was also associated with more posterior activation. Cluster extent did not predict the location of peaks but did interact with age and accuracy underlining the degree to which extent of activation may mask age- and performance-related changes in location. During error processing, accuracy (but not age) significantly predicted between individual variability in activation location. In contrast to interference processing, error processing was associated with greater within – than between – individual variability in activation location, suggesting that error processing within an individual is spread over a greater span of the MFC.
4.1. Interference processing: longitudinal distance
Within our sample, at the mean age of ∼22, mean distance of interference peak activation was ∼29 mm from the point Y = 0 along the corpus callosum (CC), localizing to the rostral, dorsal divide of the CC suggested by Steele and Lawrie (2004). The shifting of interference-related activation from rostral/anterior to dorsal/posterior MFC during development adds to prior work showing that limbic areas related to the awareness of emotionally salient information, including the ventral MFC, develop prior to dorsal MFC substrates for cognitive control regions (Perlman and Pelphrey, 2010, Somerville and Casey, 2010). Our work shows that, during interference, younger subjects recruit areas located within the MFC considered to be more active during emotion processing (Etkin and Wager, 2007, Steele and Lawrie, 2004). The three-level HLM indicated that the location difference is not due to large extent clusters, but cluster extent did interact, pointing to the necessity of controlling for this variable.
Age-related increases in dorsal/posterior and decreases in rostral/anterior MFC activation during interference have been suggested by prior work, and are supported by our topographical analysis. For example, Rubia et al. (2006) who found increased activation of cognitive control regions, including the dorsal MFC with age during inhibition, switching and interference; Adleman et al. (2002) found greater activation with age in more posterior regions of the ACC in their sample of youth from 7 to 22 years old; and Marsh et al. (2006) found a decrease in activation with age during Stroop interference in the vMFC and rACC in children, adolescents and adults. This shift has been observed in other developing cognitive domains, notably mentalization (Blakemore and Robbins, 2012), and may be associated with structural changes in white matter integrity and gray matter volumes (Blakemore, 2012, Johnson, 2011, Konrad et al., 2005).
This shift may also be a result of how the brain is responding to the task over the course of development. Because we controlled for the independent contribution of performance, age related shift in function is independent of performance in our study. However, the shift from rostral/anterior to dorsal/posterior MFC may be indicative of an underlying difference in how children and adults perform this task. Consistent with the work of Badre and D’Esposito (2009) the developmental shift we found may indicate greater automaticity in adult processing while youth may cognitively rehearse rules to a greater degree in order to achieve the same level of performance.
Prior work has also suggested the importance of controlling for age-related differences in performance, with Rubia et al. (2007) finding age-related increases in MFC activation during stop signal task designed to force a 50% fail rate in a similar healthy developmental cohort. Our use of hierarchical linear modeling allowed us to simultaneously test the effects of age and performance on location of MFC activation, while controlling for potential developmental changes in extent of that activation. In addition to becoming more dorsally located with increasing age and accuracy, MFC activation was observed to decrease in extent with development. This supports the integrative specialization theory of cognitive developmental neuroscience (Johnson, 2011) in that we observe more diffuse activation in youth and greater specialization in location of activation in adulthood.
Our work highlights the importance of location of MFC activation to the development of interference processing, showing a linear effect of age where for each year in age, activation shifts more dorsally by ∼1 mm. By taking into account the role of age, accuracy and the interacting effects of activation extent, we have demonstrated that age and accuracy follow separate but analogous topographical patterns of development, with each predictor associated to more dorsally located activation within the MFC. In fact, most of the between-individual variability in location (85%) can be accounted for by age and performance factors. Immaturity of the MFC in youth, in which limbic-associated rostral subregions develop prior to dorsally located areas for cognitive control regions (Perlman and Pelphrey, 2010), and greater reliance on rehearsal of performance rules (Badre and D’Esposito, 2009) may be responsible for increased failure to suppress interference at younger ages.
4.2. Error processing: longitudinal distance
It is important to understand brain function in tasks that mimic real world performance where youth exhibit performance deficits relative to adults. However, when controlling for performance differences and cluster extent, no significant relation of age to location of error-related activation within MFC was observed. Rather, more dorsal and posterior activation within the MFC was predicted by greater number of errors across subjects, regardless of age. This finding is consistent with other work that has identified dorsal MFC as responsive to the commission of errors (Braet et al., 2009, Stevens et al., 2009, King et al., 2010, Forster and Brown, 2011, Ichikawa et al., 2011). In contrast to interference-related activations which were more dorsal for better performing individuals, error-related activations were more rostrally located with better overall performance (i.e., lower commission error rates). Differential location of MFC activation for interference and errors in better performing individuals distinguishes these functions as separable aspects of performance monitoring, consistent with prior work (Hester et al., 2008). More rostral activation of MFC to errors has been previously observed in the context of monetary incentive to perform well (Taylor et al., 2006), and our results suggest that more rostral MFC activation to errors may enhance overall performance even in the absence of external incentive.
4.3. Interference and error: radial distance
There remained within individual unexplained variance in radial distance in both error and interference models after controlling for between individual variance in age and accuracy. This suggests that radial location of brain activity is mostly dependent on within individual variability that is not accounted for by between individual differences in age or performance.
5. Conclusions
A primary limitation of our study is that we considered only individual differences in age and accuracy, when many other factors may impact location of MFC response to performance monitoring, which varies substantially even among healthy adults (Taylor et al., 2006). In addition to developmental factors (Lamm et al., 2006, Rubia et al., 2006, Rubia et al., 2007, Fitzgerald et al., 2010) and task performance (Lamm et al., 2006, Ochsner et al., 2009, Egner, 2011), BOLD signal activations are influenced by individual variability in BOLD signal at rest (Mennes et al., 2011), task motivation (Locke and Braver, 2008), and effortful control (Urry et al., 2009). To further an understanding of developing brain function it will be necessary to better examine the role of inter and intra individual differences across a wide range of potentially influential factors (Kanai and Rees, 2011, van Horn et al., 2008). In addition, the critical role of other brain regions, outside the MFC, in performance monitoring has been well-documented (Taylor et al., 2007), underscoring the importance of considering other elements of neural circuitry in mapping development of performance monitoring function. Understanding of networked regions associated with performance monitoring would better characterize these changes as resulting from skill learning or interactive specialization over the course of development (Johnson, 2011). The results of this study suggest that children and adolescents utilize a broader section of the PFC, while adults use a more focal region of the dorsal/posterior prefrontal cortex.
Nonetheless, our work demonstrates that topographical analysis of single-subject activation patterns has the advantage of being able to examine multiple factors associated with activation patterns including individual factors (e.g., age, performance), and characteristics of the activation itself (e.g. location and extent). The introduction of HLM to the analysis allows for the separation of hierarchical nested data at inter and intra-individual levels and to estimate variance accounted for at multiple levels simultaneously (Raudenbush et al., 2004). The application of this analytic approach enables testing for age effects on aspects of brain activation, while controlling for other potentially relevant factors between and within individuals. In addition this method allows for examination of the degree of unexplained variance at different levels of analysis and to estimate the effects of variables, such as age, accuracy and extent of activation.
Despite our small sample size, we were able to determine that there is a dorsal to rostral shift in location of MFC activation during interference that is predicted by age and accuracy. This shift had been suggested by other studies, including our previous analysis of these data, however, using analysis of single-subject topographical patterns of activation and HLM, we were able to control for competing factors and estimate the degree to which development and performance determine location of BOLD signal within the MFC. This is the first study to demonstrate a progressive developmental shift in the location of MFC activation from youth to adulthood. During error, we failed to find a difference in location, intensity or extent of activation with age, but instead with accuracy, which suggest that performance may be integral to differences in development of error processing in MFC.
This study also represents a significant advance in fMRI methods. Through the consideration of multiple factors, both within and between individuals, we have controlled for individual variability in brain function, developmental change and performance differences in one analysis. The findings highlight the importance of considering development and performance differences during performance monitoring. Our data underscore that the developmental maturation of the MFC during performance monitoring accounts for significant variability between individuals in neural activity during performance monitoring.
Conflicts of interests
The authors have no conflicts of interest to disclose.
Acknowledgements
This work was supported by a National Institute of Mental Health (NIMH) Career Development Award ( 1K23-MH082176 ) to KDF, and by NIMH R01-MH6414 and R01-MH071821 to SFT. The authors would like to thank Dr. Brady West for statistical consultation and review of this manuscript.
Contributor Information
Suzanne C. Perkins, Email: sperkinz@umich.edu, sperkinz@mac.com.
Robert C. Welsh, Email: rcwelsh@med.umich.edu.
Emily R. Stern, Email: emily.stern@mssm.edu.
Stephan F. Taylor, Email: sftaylor@med.umich.edu.
Kate D. Fitzgerald, Email: krd@med.umich.edu.
References
- Adleman N.E., Menon V., Blasey C.M., White C.D., Warsofsky I.S., Glover G.H., Reiss A.L. A developmental fMRI study of the Stroop color-word task. Neuroimage. 2002;16:61–75. doi: 10.1006/nimg.2001.1046. [DOI] [PubMed] [Google Scholar]
- Badre D., D’Esposito M. Is the rostro-caudal axis of the frontal lobe hierarchical? Nat. Rev. Neurosci. 2009;10(9):659–669. doi: 10.1038/nrn2667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blakemore S.-J. Imaging brain development: the adolescent brain. Neuroimage. 2012;61:397–406. doi: 10.1016/j.neuroimage.2011.11.080. [DOI] [PubMed] [Google Scholar]
- Blakemore S.-J., Robbins T.W. Decision-making in the adolescent brain. Nat. Neurosci. 2012;15:1184–1191. doi: 10.1038/nn.3177. [DOI] [PubMed] [Google Scholar]
- Braet W., Johnson K.A., Tobin C.T., Acheson R., Bellgrove M.A., Robertson I.H., Garavan H. Functional developmental changes underlying response inhibition and error-detection processes. Neuropsychologia. 2009;47:3143–3151. doi: 10.1016/j.neuropsychologia.2009.07.018. [DOI] [PubMed] [Google Scholar]
- Bunge S.A., Dudukovic N.M., Thomason M.E., Vaidya C.J., Gabrieli J.D.E. Immature frontal lobe contributions to cognitive control in children: evidence from fMRI. Neuron. 2002;33:301–311. doi: 10.1016/s0896-6273(01)00583-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bush G., Shin L.M., Holmes J., Rosen B. The Multi-Source Interference Task: validation study with fMRI in individual subjects. Mol. Psychiatry. 2003;8:60–70. doi: 10.1038/sj.mp.4001217. [DOI] [PubMed] [Google Scholar]
- Casey B.J., Jones R.M., Hare T.A. The adolescent brain. Ann. N. Y. Acad. Sci. 2008;1124:111–126. doi: 10.1196/annals.1440.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casey B.J., Jones R.M., Levita L., Libby V., Pattwell S.S., Ruberry E.J., Soliman F., Somerville L.H. The storm and stress of adolescence: insights from human imaging and mouse genetics. Dev. Psychobiol. 2010;52:225–235. doi: 10.1002/dev.20447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durston S., Davidson M.C., Tottenham N., Galvan A., Spicer J., Fossella J.A., Casey B.J. A shift from diffuse to focal cortical activity with development. Dev. Sci. 2006;9:1–8. doi: 10.1111/j.1467-7687.2005.00454.x. [DOI] [PubMed] [Google Scholar]
- Egner T. Right ventrolateral prefrontal cortex mediates individual differences in conflict-driven cognitive control. J. Cognitive Neurosci. 2011;23:3903–3913. doi: 10.1162/jocn_a_00064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Etkin A., Wager T.D. Functional neuroimaging of anxiety: a meta-analysis of emotional processing in PTSD, social anxiety disorder, and specific phobia. Am. J. Psychiatry. 2007;164:1476–1488. doi: 10.1176/appi.ajp.2007.07030504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- First M., Spitzer R., Miriam G., Williams J.B. American Psychiatric Press, Inc; Washington, D.C.: 1996. Structured Clinical Interview for DSM-IV Axis I Disorders, Clinician Version (SCID-CV) [Google Scholar]
- Fitzgerald K.D., Perkins S.C., Angstadt M., Johnson T., Stern E.R., Welsh R.C., Taylor S.F. The development of performance-monitoring function in the posterior medial frontal cortex. Neuroimage. 2010;49:3463–3473. doi: 10.1016/j.neuroimage.2009.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forster S.E., Brown J.W. Medial prefrontal cortex predicts and evaluates the timing of action outcomes. Neuroimage. 2011;55:253–265. doi: 10.1016/j.neuroimage.2010.11.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hester R., Barre N., Murphy K., Silk T.J., Mattingley J.B. Human Medial Frontal Cortex Activity Predicts Learning from Errors. Cereb. Cortex. 2008;18(8):1933–1940. doi: 10.1093/cercor/bhm219. [DOI] [PubMed] [Google Scholar]
- Ichikawa N., Siegle G.J., Jones N.P., Kamishima K., Thompson W.K., Gross J.J., Ohira H. Feeling bad about screwing up: emotion regulation and action monitoring in the anterior cingulate cortex. Cogn. Affect Behav. Neurosci. 2011;11:354–371. doi: 10.3758/s13415-011-0028-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson M.H. Interactive specialization: a domain-general framework for human functional brain development? Accident Anal. Prev. 2011;1:7–21. doi: 10.1016/j.dcn.2010.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanai R., Rees G. The structural basis of inter-individual differences in human behaviour and cognition. Nat. Rev. Neurosci. 2011;12:231–242. doi: 10.1038/nrn3000. [DOI] [PubMed] [Google Scholar]
- Kaufman J., Birmaher B., Brent D., Rao U., Flynn C., Moreci P., Williamson D., Ryan N. Schedule for affective disorders and schizophrenia for school-age children-present and lifetime version (K-SADS-PL): initial reliability and validity data. J. Am. Acad. Child Psychiatry. 1997;36:980–988. doi: 10.1097/00004583-199707000-00021. [DOI] [PubMed] [Google Scholar]
- King J.A., Korb F.M., von Cramon D.Y., Ullsperger M. Post-error behavioral adjustments are facilitated by activation and suppression of task-relevant and task-irrelevant information processing. J. Neurosci. 2010;30:12759–12769. doi: 10.1523/JNEUROSCI.3274-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konrad K., Neufang S., Thiel C.M., Specht K., Hanisch C., Fan J., Herpertz-Dahlmann B., Fink G.R. Development of attentional networks: an fMRI study with children and adults. Neuroimage. 2005;28:429–439. doi: 10.1016/j.neuroimage.2005.06.065. [DOI] [PubMed] [Google Scholar]
- Lamm C., Zelazo P.D., Lewis M.D. Neural correlates of cognitive control in childhood and adolescence: disentangling the contributions of age and executive function. Neuropsychologia. 2006;44:2139–2148. doi: 10.1016/j.neuropsychologia.2005.10.013. [DOI] [PubMed] [Google Scholar]
- Locke H.S., Braver T.S. Motivational influences on cognitive control: behavior, brain activation, and individual differences. Cogn. Affect. Behav. Neurosci. 2008;8:99–112. doi: 10.3758/cabn.8.1.99. [DOI] [PubMed] [Google Scholar]
- Marsh R., Zhu H., Schultz R.T., Quackenbush G., Royal J., Skudlarski P., Peterson B.S. A developmental fMRI study of self-regulatory control. Hum. Brain Mapp. 2006;27:848–863. doi: 10.1002/hbm.20225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mennes M., Zuo X.N., Kelly C., Di Martino A., Zang Y.F., Biswal B., Castellanos F.X., Milham M.P. Linking inter-individual differences in neural activation and behavior to intrinsic brain dynamics. Neuroimage. 2011;54:2950–2959. doi: 10.1016/j.neuroimage.2010.10.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ochsner K.N., Hughes B., Robertson E.R., Cooper J.C., Gabrieli J.D.E. Neural systems supporting the control of affective and cognitive conflicts. J. Cogn. Neurosci. 2009;1:1842–1855. doi: 10.1162/jocn.2009.21129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perlman S.B., Pelphrey K.A. Regulatory brain development: balancing emotion and cognition. Soc. Neurosci. 2010;5:533–542. doi: 10.1080/17470911003683219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raudenbush S., Bryk A. second ed. Sage Publications; Thousand Oaks, CA: 2002. Hierarchical Linear Models: Applications and Data Analysis Methods; p. 485. [Google Scholar]
- Raudenbush S., Bryk A. Scientific Software International, Inc; Lincolnwood, IL: 2004. HLM 6 [Computer software] [Google Scholar]
- Raudenbush S., Bryk A., Cheong Y., Congdon R. Scientific Software International; Lincolnwood, IL: 2004. HLM 6: Hierarchical Linear and Nonlinear Modeling. [Google Scholar]
- Ridderinkhof K.R. The Role of the Medial Frontal Cortex in Cognitive Control. Science. 2004;306(5695):443–447. doi: 10.1126/science.1100301. [DOI] [PubMed] [Google Scholar]
- Rubia K., Smith A.B., Taylor E., Brammer M.J. Linear age-correlated functional development of right inferior fronto-striato-cerebellar networks during response inhibition and anterior cingulate during error-related processes. Hum. Brain Mapp. 2007;28:1163–1177. doi: 10.1002/hbm.20347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubia K., Smith A.B., Woolley J., Nosarti C., Heyman I., Taylor E., Brammer M.J. Progressive increase of frontostriatal brain activation from childhood to adulthood during event-related tasks of cognitive control. Hum. Brain Mapp. 2006;27:973–993. doi: 10.1002/hbm.20237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeter M.L., Zysset S., Wahl M., von Cramon D.Y. Prefrontal activation due to Stroop interference increases during development – an event-related fNIRS study. Neuroimage. 2004;23:1317–1325. doi: 10.1016/j.neuroimage.2004.08.001. [DOI] [PubMed] [Google Scholar]
- Somerville L.H., Casey B.J. Developmental neurobiology of cognitive control and motivational systems. Curr. Opin. Neurobiol. 2010;20:236–241. doi: 10.1016/j.conb.2010.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steele J.D., Lawrie S.M. Segregation of cognitive and emotional function in the prefrontal cortex: a stereotactic meta-analysis. Neuroimage. 2004;21:868–875. doi: 10.1016/j.neuroimage.2003.09.066. [DOI] [PubMed] [Google Scholar]
- Stenger V.A., Boada F.E., Noll D.C. Multishot 3D slice-select tailored RF pulses for MRI. Magn. Reson. Med. 2002;48:157–165. doi: 10.1002/mrm.10194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern E.R., Welsh R.C., Fitzgerald K.D., Taylor S.F. Topographic analysis of individual activation patterns in medial frontal cortex in schizophrenia. Hum. Brain Mapp. 2009;30:2146–2156. doi: 10.1002/hbm.20657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens M.C., Kiehl K.A., Pearlson G.D., Calhoun V.D. Brain network dynamics during error commission. Hum. Brain Mapp. 2009;30:24–37. doi: 10.1002/hbm.20478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor S.F., Martis B., Fitzgerald K.D., Welsh R.C., Abelson J.L., Liberzon I., Himle J.A., Gehring W.J. Medial frontal cortex activity and loss-related responses to errors. J. Neurosci. 2006;26:4063–4070. doi: 10.1523/JNEUROSCI.4709-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor S.F., Stern E.R., Gehring W.J. Neural systems for error monitoring: recent findings and theoretical perspectives. Neuroscientist. 2007;13:160–172. doi: 10.1177/1073858406298184. [DOI] [PubMed] [Google Scholar]
- Urry H.L., van Reekum C.M., Johnstone T., Davidson R.J. Individual differences in some (but not all) medial prefrontal regions reflect cognitive demand while regulating unpleasant emotion. Neuroimage. 2009;47:852–863. doi: 10.1016/j.neuroimage.2009.05.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Horn J.D., Grafton S.T., Miller M.B. Individual variability in brain activity: a nuisance or an opportunity? Brain Imaging Behav. 2008;2:327–334. doi: 10.1007/s11682-008-9049-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velanova K., Wheeler M.E., Luna B. Maturational changes in anterior cingulate and frontoparietal recruitment support the development of error processing and inhibitory control. Cereb. Cortex. 2008;18(11):2505–2522. doi: 10.1093/cercor/bhn012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velanova K., Wheeler M.E., Luna B. The maturation of task set-related activation supports late developmental improvements in inhibitory control. J. Neurosci. 2009;29:12558–12567. doi: 10.1523/JNEUROSCI.1579-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worsley K.J., Friston K.J. Analysis of fMRI time-series revisited – again. Neuroimage. 1995;2:173–181. doi: 10.1006/nimg.1995.1023. [DOI] [PubMed] [Google Scholar]
- Worsley K.J., Liao C.H., Aston J., Petre V., Duncan G.H., Morales F., Evans A.C. A general statistical analysis for fMRI data. Neuroimage. 2002;15:1–15. doi: 10.1006/nimg.2001.0933. [DOI] [PubMed] [Google Scholar]
- Yang Y., Gu H., Zhan W., Xu S., Silbersweig D.A., Stern E. Simultaneous perfusion and BOLD imaging using reverse spiral scanning at 3T: characterization of functional contrast and susceptibility artifacts. Magn. Reson. Med. 2002;48:278–289. doi: 10.1002/mrm.10196. [DOI] [PubMed] [Google Scholar]