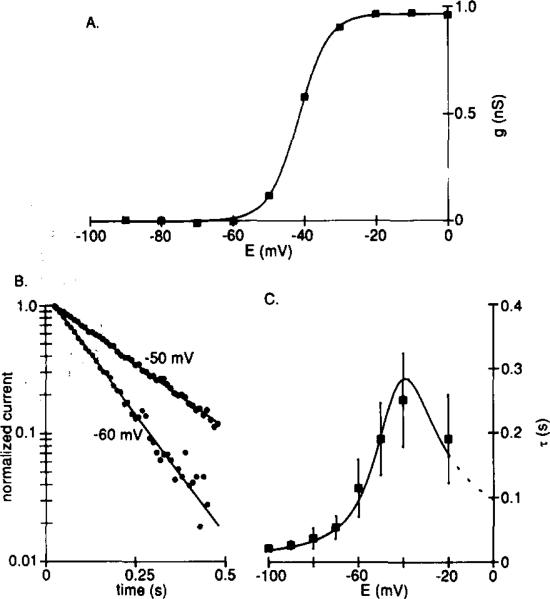
Figure 3. Time and Voltage Dependence of I_Kx.

Recordings were made from ceils bathed in Ringer solution containing 5 mM Cs⁺ and 0.1 mM Cd²⁺.

(A) Voltage dependence of activation for a typical experiment. Peak tail currents at –30 mV (the same protocol as shown in Figure 2A) were converted to conductance and plotted against conditioning potential. The reversal potential for I_Kx was taken as –74 mV (see Figure 4), zero conductance corresponds to the minimum value of g_Kx, and the smooth curve is the Boltzmann equation fitted using a least-squares method.

(B) Deactivation of I_Kx described by a single exponential. Hyperpolarizing voltage steps (1 s) were applied from a holding potential of –30 mV, and exponentials were fitted to the current decay using a nonlinear least-squares method. The currents (circles) and exponentials (continuous lines) are shown normalized and on a semilogarithmic scale for two test potentials.

(C) Time constants (τ) of exponentials fitted to the decay of I_Kx (means ± SD, n = 5–8) plotted against test potential. The smooth curve is 1/(α + β), in which α and β are rate constants for transitions between the closed and open states of the channels. Mean values for α and β (n = 6) were calculated from α = A_∞/τ and β = (1 – A_∞)/τ (Hodgkin and Huxley, 1952), in which A_∞ is the normalized steady-state conductance, and τ is the time constant (s) of the fitted exponential. α and β were fitted by eye with the functions: α = 0.23(E + 45)/(1 – exp(– (E + 45)/7)); β = 1.2(E + 55)/(exp((E + 55)/5.5) – 1), in which E is the membrane potential (mV).