Monte Carlo SURE-Based Parameter Selection for Parallel Magnetic Resonance Imaging Reconstruction

Abstract

Purpose

Regularizing parallel MRI reconstruction significantly improves image quality but requires tuning parameter selection. We propose a Monte Carlo method for automatic parameter selection based on Stein’s unbiased risk estimate (SURE) that minimizes the multi-channel k-space mean squared error (MSE). We automatically tune parameters for image reconstruction methods that preserve the undersampled acquired data, which cannot be accomplished using existing techniques.

Theory

We derive a weighted MSE criterion appropriate for data-preserving regularized parallel imaging reconstruction and the corresponding weighted SURE. We describe a Monte Carlo approximation of the weighted SURE that uses two evaluations of the reconstruction method per candidate parameter value.

Methods

We reconstruct images using the sparsity-promoting methods DESIGN and L₁-SPIRiT. We validate Monte Carlo SURE against the weighted MSE. We select the regularization parameter using these methods for various noise levels and undersampling factors and compare the results to those using MSE-optimal parameters.

Results

Our method selects nearly MSE-optimal regularization parameters for both DESIGN and L₁-SPIRiT over a range of noise levels and undersampling factors.

Conclusion

The proposed method automatically provides nearly MSE-optimal choices of regularization parameters for data-preserving nonlinear parallel MRI reconstruction methods.

INTRODUCTION

While SENSE (1), GRAPPA (2), and SPIRiT (3) successfully reconstruct full field-of-view (FOV) images from undersampled parallel MRI data, many recent developments improve upon these methods using regularization (4–7). Practical clinical use of such methods requires selecting appropriate values of the regularization parameter(s). Often, a developer hard-codes a single value that “works” over a range of tested situations, or a user tunes the parameter manually for their particular application. When the scanning protocol remains unchanged across many subjects, such reuse may be justifiable. However, in cases where image contrast varies, some users may wish to ensure that their regularization parameters are reasonable.

The problem of regularization parameter selection has a long history, leading to a variety of techniques. In an extended scan session, one can adapt regularization parameters using data acquired earlier in the scan (8). However, such adaptations require acquiring and reconstructing a high quality data set initially without regularization. Many applications cannot provide such a ground truth acquisition. For example, accelerated diffusion weighted imaging can use shorter echo times, so an un-accelerated “ground truth” may actually have reduced image quality (9): a longer single-shot sequence would have greater geometric distortions and reduced contrast and signal from the long echo time. A multi-shot acquisition would take much longer, making motion and fatigue potential issues. Dynamic studies such as abdominal or cardiac perfusion imaging are corrupted by motion and other time-varying effects that are hard to replicate to produce a ground truth suitable for regularization. The same goes for dynamic contrast enhanced studies. Functional MRI is another area where ground truths are often inaccessible due to limited temporal resolution and non-repeatability of the underlying dynamic processes. While one could ignore these dynamics when they are small in amplitude, as is the case with functional activation, doing so risks selecting parameters that would not adequately preserve these small deviations in the reconstruction.

Other techniques automatically tune regularization parameters based on a statistical model of the noise and just the acquired data (no training set). Among the most well-known, the discrepancy principle (10), generalized cross-validation (11,12), and L-curve curvature maximization (4,13,14) are founded in mathematical theory derived for quadratic regularizers with closed-form solutions. Their extension to nonlinear regularization is limited (15, 16). All these methods rely on the measurement residual, the difference between the acquired (noisy) data and the measurement model applied to the reconstructed image(s), to tune parameters. Thus, these methods are ineffective when the acquired data is preserved by the reconstruction method, since the resulting residual is exactly zero, regardless of the regularization parameter values. Although noisy, the acquired data contains essential details that could be compromised by regularization, so many image reconstruction techniques aim to preserve the acquired data, including regularized parallel imaging techniques like DESIGN (6) and L₁-SPIRiT (3, 7, 17, 18). In this paper, we propose a new error criterion that is appropriate for data-preserving regularized reconstruction methods, for which we derive a novel parameter selection scheme.

We seek the parameter that minimizes the k-space mean squared error (MSE) for reconstruction methods based on nonlinear regularizers such as the ℓ₁ norm commonly used to promote sparsity (19). Although k-space MSE may not be sensitive to local image errors in small features of diagnostic value, it is a convenient quality measure used frequently in the literature. MSE is the basis for many image reconstruction methods, including SENSE, which yields the MSE-optimal combined image consistent with the multi-channel data, when given correct coil sensitivities (1). Since calculating the actual MSE would require knowing the true image, we turn to Stein’s unbiased risk estimate (SURE) (20), which approximates the MSE for a Gaussian noise model and accommodates nonlinear reconstruction algorithms. Using the noise model and partial derivatives of the reconstruction function, SURE yields an expression that is equal in expected value to the MSE and can be minimized to select a suitable regularization parameter value without knowing the true signal.

SURE has been exploited for parameter selection in denoising (21–23), deblurring (24–26), single-channel MRI (16,27), and image-domain non-iterative SENSE reconstruction (28) for uniform (nonrandom) undersampled parallel MRI. However, in its basic formulation, evaluating SURE involves computing the Jacobian matrix of the targeted reconstruction function. While feasible, analytically evaluating SURE is difficult for iterative methods and requires exactly differentiating nearly every computation performed in a particular implementation. A Monte Carlo SURE framework (23, 27) was derived to avoid this complication, also motivating this work. The original derivation of the Monte Carlo framework, and of SURE in general, is restricted to the denoising setting, where the entire image is observed. Later work extends SURE to inverse problems such as image reconstruction, using modified error metrics such as predicted-MSE or projected-MSE (16, 25–27). However, such frameworks share the limitation of discrepancy principle, cross validation, and L-curve-based methods, that the criteria are based on the measurement residual, which is insensitive to the parameter choice for data-preserving reconstructions. That limitation also extends to the Monte Carlo nonlinear generalized cross validation method described previously (16).

We extend the Monte Carlo SURE framework to regularized auto-calibrating parallel MRI reconstruction methods that preserve the data. The novelty of our method consists of applying parallel imaging to express the un-acquired (or full) k-space error criterion in terms of just the k-space that we measure. This approach avoids the complications that arise from data discrepancy but limits our method to parallel imaging applications. We demonstrate the generality and utility of this method using two regularized iterative algorithms on real data: DESIGN (6) and L₁-SPIRiT (3,7). The first improves upon GRAPPA with uniform undersampling, while the second applies compressed sensing (19) to random Cartesian undersampling. In preliminary studies, we described the extension to parallel imaging with uniform Cartesian undersampling and depicted simulated data using SURE-optimized DESIGN (29), and we applied SURE to L₁-SPIRiT for a range of synthetic noise levels (30). Here, we validate the Monte Carlo estimate of the weighted SURE criterion against the true weighted MSE for both parallel-imaging methods and apply the proposed method to DESIGN for different noise levels and to L₁-SPIRiT for various undersampling factors. We conclude with a discussion of the implications of a general algorithm for automatic parameter selection and useful extensions of this work.

THEORY

Parallel imaging reconstruction methods like SENSE (1) use coil sensitivity profiles to reconstruct a single full-FOV combined image from multiple coil channels of undersampled k-space data. However, coil sensitivities may be difficult to measure accurately, motivating auto-calibrating methods like GRAPPA (2) or SPIRiT (3) that do not require explicit knowledge of those profiles. These methods typically operate in the k-space domain and fill the Cartesian k-space grid for every coil, so the MSE of the full multi-channel k-space is the cost function we aim to minimize. Methods like sum-of-squares (31) can be used to combine these full-FOV data sets afterwards.

Measurement Model and Error Criteria

The target Cartesian k-space grid for an N-voxel volume can be represented as a length-N vector; for P coils, these vectors stack to form the length-NP vector x. We undersample k-space, acquiring M < N points arranged in some fashion, and represented as a length-M vector. The sampling pattern for each receive coil is identical; we combine these vectors into a length-MP vector y. The full k-space relates to the acquired data via the linear equation y = Mx. When our sampling pattern is Cartesian, M is a simple MP × NP mask, where each row has a single entry equal to one and all the other elements equal to zero. To complete our model, we consider our measurements to be contaminated with additive complex Gaussian noise η, independent across k-space locations, and correlated across channels, with zero mean and covariance Λ:

$$\mathbf{y}=\mathbf{Mx}+\mathit{\eta }.$$ [1]

To reconstruct the full k-space x from our noisy samples y, we focus on improving auto-calibrating linear methods like GRAPPA and SPIRiT. The regularized version of these methods is in general nonlinear and can be written as x̂ = f_γ(y), where user-specified parameter(s) γ control the level of regularization.

To guide selection of the regularization parameters γ, one might aim to use a criterion based on the MSE of the full multi-channel k-space:

$$\text{MSE}(\mathit{\gamma })\triangleq {\Vert \mathbf{x}-{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y})\Vert }_2^2,$$ [2]

which is a function of the unknown true values of the full k-space x. When applied to Cartesian under-sampled data, we are interested in preserving the acquired data in the reconstruction, so Mf_γ(y) = y, regardless of the value of γ. Thus, we attempt to minimize the MSE weighted over the set of un-acquired k-space points:

$$\text{WMSE}(\mathit{\gamma })\triangleq {\Vert \stackrel{\sim }{\mathbf{M}}(\mathbf{x}-{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y}))\Vert }_2^2,$$ [3]

where M̃ is the mask complementary to M for Cartesian undersampled data. One can use the weighted MSE (WMSE) criterion directly only if one postulates a Bayesian prior model for x. Since such priors are rarely realistic for medical images, we take a non-Bayesian approach where x is deterministic but unknown.

Applying SURE to WMSE Using Parallel Imaging

SURE is an unbiased estimate of the MSE of some unknown vector x from direct measurements y = x + η corrupted by Gaussian noise η. Thus, approximating the WMSE (or MSE) of the un-acquired (or full) multi-channel k-space would require directly measuring the entire k-space x to apply SURE. Since we undersample k-space, we essentially need to invert the measurement matrix M in Eq. [1] to minimize the WMSE in Eq. [3]. Since the measurement matrix undersamples k-space, M is singular, and such an inversion naturally would be ill-posed. This key problem is avoided in previous work by modifying the error criterion to be a function of the measurement error only, like projected-MSE and predicted-MSE (16, 25–27), which apply the measurement mask M to the reconstructed image(s). However, such efforts do not work for reconstructions that retain the measurements. Our novel contribution uses parallel imaging to perform the necessary inversion. We introduce the linear operator G that estimates the full multi-channel k-space from the true k-space values at the sampled locations. For instance, un-regularized parallel imaging methods like GRAPPA and SPIRiT provide approximately true values of the full multi-channel k-space when no noise is present: x ≈ GMx. Thus, we write

$$\text{WMSE}(\mathit{\gamma })\approx {\Vert \stackrel{\sim }{\mathbf{M}}(\mathbf{GMx}-{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y}))\Vert }_2^2.$$ [4]

Given a properly calibrated G and an appropriate level of undersampling for the number of channels and geometry of the array coil, minimizing this criterion should nearly optimize the true weighted MSE, and minimizing the SURE for this error should yield γ that is also nearly WMSE-optimal. In the examples using DESIGN and L₁-SPIRiT as the regularized reconstruction f_γ(y), we choose the linear mapping G to be the un-regularized version of the reconstruction f_γ(y), namely GRAPPA and SPIRiT, respectively. However, the theory does not require any such connection between G and f_γ(y). We emphasize that we do not need to consider noise amplification in choosing G, since G is applied to noise-free Mx in our derivation, not to our actual observations y. However, the number of available coils and the desired acceleration factor can influence the accuracy of this approximation, so we investigate the effects of violating this assumption in our experiments. This use of G for regularization parameter selection is unique to this work, and the last subsection of the Methods section investigates how this approximation affects parameter selection.

Monte Carlo SURE Approximation

Expanding the approximate WMSE in Eq. [4], and using Eq. [1],

$$\text{WMSE}(\mathit{\gamma })\approx {\Vert \stackrel{\sim }{\mathbf{M}}\mathbf{GMx}\Vert }_2^2+{\Vert \stackrel{\sim }{\mathbf{M}}{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y})\Vert }_2^2-2\mathcal{R}e\{{\mathbf{y}}^{\prime }{\mathbf{G}}^{\prime }{\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{M}}{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y})\}+2\mathcal{R}e\{{\mathit{\eta }}^{\prime }{\mathbf{G}}^{\prime }{\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{M}}{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y})\},$$ [5]

where [·]′ denotes the conjugate transpose operator. The WMSE isolates x to the first term of Eq. [5], which does not depend on γ, so it can be considered a constant C and ignored when optimizing γ. The next two terms of Eq. [5] can be computed directly using f_γ(y) and Gy, but the last term is a function of both γ and the unknown noise vector η. Stein’s lemma (16, 20, 25) approximates this last term, so that we can find γ that minimizes the WMSE. Without our parallel-imaging-based approximation of the full k-space, we could not express the un-acquired multi-channel k-space in terms of the acquired data and the noise, and there would be no noise term in Eq. [5] to approximate using Stein’s lemma.

Now, we modify previous derivations of Monte Carlo SURE (23, 27) to include the matrix G. When f_γ(y) is (sub-) differentiable, let J_fγ(y) be the Jacobian matrix of all first order partial (sub-) derivatives of f_γ(y) with respect to y. Using the chain rule for derivatives, the Jacobian of the expression G′M̃′M̃f_γ(y) is G′M̃′M̃J_fγ(y). This expression in combination with Stein’s lemma implies (27) that

$$\mathcal{E}\{{\mathit{\eta }}^{\prime }{\mathbf{G}}^{\prime }{\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{M}}{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y})\}=\mathcal{E}\{\text{tr}\{\mathbf{\Lambda }{\mathbf{G}}^{\prime }{\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{M}}{\mathbf{J}}_{{\mathbf{f}}_{\mathit{\gamma }}}(\mathbf{y})\}\}.$$ [6]

Applying Eq. [6] to the approximate WMSE in Eq. [5] yields the weighted SURE (WSURE) function, which is an unbiased estimate of the WMSE:

$$\text{WSURE}(\mathit{\gamma })={\Vert \stackrel{\sim }{\mathbf{M}}{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y})\Vert }_2^2-2\mathcal{R}e\{{\mathbf{y}}^{\prime }{\mathbf{G}}^{\prime }{\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{M}}{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y})\}+2\mathcal{R}e\{\text{tr}(\mathbf{\Delta }{\mathbf{G}}^{\prime }{\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{M}}{\mathbf{J}}_{{\mathbf{f}}_{\mathit{\gamma }}}(\mathbf{y}))\}+C.$$ [7]

However, this expression involves computing all the partial derivatives of the reconstruction function. For iterative reconstructions, the Jacobian matrix could be computed step-by-step, but such an approach requires a careful derivation customized for that particular reconstruction method (16, 24, 26). For an iterative reconstruction like DESIGN and L₁-SPIRiT, expressions for the Jacobian matrices must be derived for each step in the implementation. Instead, we use Monte Carlo SURE (23, 27), which does not require such in-depth knowledge of the algorithm under consideration. Under mild conditions on f_γ(y) (23,27,29), the directional derivative J_fγ(y)b can be approximated by

$$\mathit{\rho }(\mathbf{y},\mathbf{b},\epsilon )=({\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y}+(\epsilon {\Vert \mathbf{y}\Vert }_2/\sqrt{MP})\mathbf{b})-{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y}))/(\epsilon {\Vert \mathbf{y}\Vert }_2/\sqrt{MP}),$$ [8]

for sufficiently small ε > 0. The scale factor ${\Vert \mathbf{y}\Vert }_2/\sqrt{MP}$ adjusts ε for the relative scale of the data; this is motivated by the fact that some algorithms (like DESIGN) use an un-normalized Fourier transform to relate k-space to image space, while others (like L₁-SPIRiT) use a normalized transform. Then, choosing b to be a vector of independent, identically distributed complex zero-mean, unit-variance Bernoulli-distributed random variables (i.e., the real and imaginary parts of each element of b are drawn independently from { $\pm 1/\sqrt{2}$} with equal probability), we form a Monte Carlo approximation to the trace of the Jacobian (23,27) with just one realization of b:

$$\text{tr}\{\mathbf{\Lambda }{\mathbf{G}}^{\prime }{\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{M}}{\mathbf{J}}_{{\mathbf{f}}_{\mathit{\gamma }}}(\mathbf{y})\}\approx {\mathbf{b}}^{\prime }\mathbf{\Lambda }{\mathbf{G}}^{\prime }{\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{M}}\mathit{\rho }(\mathbf{y},\mathbf{b},\epsilon ),$$ [9]

Plugging this approximation into Eq. [7] yields the Monte Carlo estimate of WSURE:

$$\text{WSURE}(\mathit{\gamma })\approx {\Vert \stackrel{\sim }{\mathbf{M}}{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y})\Vert }_2^2-2\mathcal{R}e\{{\mathbf{y}}^{\prime }{\mathbf{G}}^{\prime }{\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{M}}{\mathbf{f}}_{\mathit{\gamma }}(\mathbf{y})\}+2\mathcal{R}e\{{\mathbf{b}}^{\prime }\mathbf{\Lambda }{\mathbf{G}}^{\prime }{\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{M}}\mathit{\rho }(\mathbf{y},\mathbf{b},\epsilon )\}+C.$$ [10]

The same b can be used for evaluating WSURE with different choices of regularization parameter, so we can compute and store M̃GΛb just once. When we apply WSURE to regularized GRAPPA or SPIRiT reconstructions, we can find the parameters γ that minimize WSURE using a derivative-free minimization algorithm. In this work, we deal with scalar γ, and we employ a coarse-to-fine parameter sweep, where we evaluate WSURE for successively narrower intervals of γ.

Next, we summarize two regularized reconstruction methods that illustrate the broad applicability of Monte Carlo WSURE to regularization parameter selection: DESIGN (6) and L₁-SPIRiT (3, 7). GRAPPA is a popular and time-tested auto-calibrating parallel imaging reconstruction method for uniformly spaced undersampled k-space data. The regularized method DESIGN is attractive from a computational standpoint because it denoises the GRAPPA reconstruction output, instead of iteratively reapplying GRAPPA to denoised data, which would be slower. L₁-SPIRiT also is a useful example of an auto-calibrating regularized reconstruction method because it can readily process nonuniformly or randomly undersampled k-space data.

DESIGN: Sparsity-promoting GRAPPA

For uniformly undersampled Cartesian k-space, the GRAPPA reconstruction directly fills missing k-space in all the coil array channels with a linear combination of neighboring acquired points weighted by a shift-invariant kernel. GRAPPA reconstruction is implemented efficiently using convolution or the Fast Fourier Transform (FFT). For R_x × R_y two-dimensional undersampled 2D k-space, the GRAPPA method using a set of B_x × B_y 2D kernels g_p,q,rx,ry [b_x, b_y] for each input/output channel pair (p, q) and target frequency shift (r_x, r_y) evaluates

$$\widehat{x}[k_x+r_x,k_y+r_y,q]=\sum _{p=1}^P\sum _{b_x=-B_x/2}^{B_x/2}\sum _{b_y=-B_y/2}^{B_y/2}{g}_{p,q,r_x,r_y}[b_x,b_y]·y[k_x+b_x{R}_x,k_y+b_y{R}_y,p].$$ [11]

These GRAPPA kernels are calibrated the usual way, using a least-squares fit with densely sampled k-space training data, potentially with regularization. Then, we regularize the GRAPPA reconstruction using a null space formulation of the data-preserving DESIGN method (6):

$${\mathbf{f}}_{\gamma }(\mathbf{y})={\stackrel{\sim }{\mathbf{M}}}^{\prime }{\stackrel{\sim }{\mathbf{x}}}^{\ast }+{\mathbf{M}}^{\prime }\mathbf{y};{\stackrel{\sim }{\mathbf{x}}}^{\ast }=\underset{\stackrel{\sim }{\mathbf{x}}}{argmin}\frac{1}{2}{\Vert {({\mathbf{\Lambda }}_G)}^{-\frac{1}{2}}(\stackrel{\sim }{\mathbf{x}}-\stackrel{\sim }{\mathbf{M}}\mathbf{Gy})\Vert }_2^2+\gamma {\Vert \mathbf{\Psi }{\mathcal{F}}^{-1}({\stackrel{\sim }{\mathbf{M}}}^{\prime }\stackrel{\sim }{\mathbf{x}}+{\mathbf{M}}^{\prime }\mathbf{y})\Vert }_{1,2},$$ [12]

where x̃/x̃^* is the length-(N − M)P vector of missing k-space for all the coil channels, Λ_G is the noise covariance of the GRAPPA-reconstructed missing data Λ_G = M̃GΛG′M̃′, γ is the regularization parameter of interest, Ψ is the linear sparsifying transform, 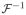is the inverse FFT, and ||·||_1,2 is the joint sparsity-promoting hybrid ℓ₁/ℓ₂ norm. To evaluate this mixed norm, for each transform coefficient, we form a vector of that coefficient’s values across all the coil channels, and we compute the sum of the ℓ₂ norms of these vectors. The matrix G corresponds to convolving the GRAPPA kernels with the under-sampled k-space. Because GRAPPA introduces correlations among many frequencies into the noise covariance Λ_G, and such a covariance matrix is expensive to store or invert, we simplify the matrix by ignoring the correlations across frequencies, considering only the noise amplification and correlation across coils (32). The resulting optimization problem can be implemented using any number of algorithms; we use a Split-Bregman approach (33) with auxiliary variable w = Ψ 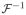(M̃′x̃′ + M′y).

Sparsity-regularized SPIRiT

While GRAPPA is effective for uniformly-spaced Cartesian undersampling, a more flexible method is desirable for nonuniformly undersampled k-space. The SPIRiT reconstruction method is an iterative formulation that uses kernel-weighted linear consistency equations similar to the GRAPPA convolution equation in [11] to estimate missing k-space data. However, SPIRiT consistency equations operate over the entire k-space, including un-acquired frequencies. For a 2D B_x × B_y kernel s_p,q[b_x, b_y] with s_q,q[0, 0] = 0, the consistency equation for the point x[k_x, k_y, q] is

$$x[k_x,k_y,q]=\sum _{p=1}^P\sum _{b_x=-B_x/2}^{B_x/2}\sum _{b_y=-B_y/2}^{B_y/2}{s}_{p,q}[b_x,b_y]x[k_x+b_x,b_y+b_y,p].$$ [13]

The data-preserving version of SPIRiT forms a linear system x = Sx of these consistency equations over all of multi-channel k-space and minimizes the least-squares fit constrained by the data consistency equation y = Mx:

$$\mathbf{Gy}=\underset{\mathbf{x}}{argmin}{\Vert (\mathbf{S}-\mathbf{I})\mathbf{x}\Vert }_2^2\text{subject}\text{to}\mathbf{y}=\mathbf{Mx}.$$ [14]

This constrained optimization problem can be regularized using an additional sparsity term on the wavelet-transformed images obtained by taking the inverse FFT of the full multi-channel k-space, yielding the regularized problem

$${\mathbf{f}}_{\gamma }(\mathbf{y})=\underset{\mathbf{x}}{argmin}\frac{1}{2}{\Vert (\mathbf{S}-\mathbf{I})\mathbf{x}\Vert }_2^2+\gamma {\Vert \mathbf{\Psi }{\mathcal{F}}^{-1}\mathbf{x}\Vert }_{1,2}\text{subject}\text{to}\mathbf{y}=\mathbf{Mx}.$$ [15]

The projection-onto-convex-sets-based implementation called L₁-SPIRiT (7) uses a sparsity-promoting shrinkage operation on the sparse transform of x, controlled by the predetermined scalar threshold γ.

METHODS

We demonstrate our parameter selection method on real data from consented subjects in accordance with IRB-approved protocols using a GE Discovery 3T MRI scanner with a vendor-supplied 8-channel array coil. We performed six repetitions of a T1-weighted 3D spoiled gradient echo sequence (TR = 10.1 ms, TE = 4.3 ms, FA = 16 degrees, BW = 31.25 kHz) to sample a 256 × 256 × 10 Cartesian multi-channel reference volume with 24×24×3 cm FOV, 0.94×0.94×3.0 mm resolution, and no acceleration. We separately saved four repetitions of a T1-weighted 2D spoiled gradient echo sequence (TR = 20.0 ms, TE = 9.1 ms, FA = 10 degrees, BW = 15.63 kHz) to sample a 256 × 256 multi-channel axial slice with 24 × 24 cm FOV, 0.94 × 0.94 × 4.0 mm resolution, with no acceleration, similar to T1-weighted slice-by-slice acquisitions used for overlaying anatomical information. We used 3D and 2D acquisitions to add generality to the data sets for validation purposes. The averaged data are used as low-noise reference images for the experiments that follow.

We processed the acquired raw multi-channel data using MATLAB. Both T1-weighted images were cropped tightly around the subject’s head before undersampling and reconstructing the data. Then, we undersampled an axial slice of the reference volume using the desired sampling scheme (uniform or nonuniform Cartesian), and we reconstructed the data using the auto-calibrating method of choice (GRAPPA-based DESIGN for uniform Cartesian sampling or L₁-SPIRiT for nonuniform). Since we are interested in reconstructing images without sensitivity maps, we formed combined images using a sum-of-squares algorithm (31). Reconstructed images are evaluated against the ground truth (when available) using difference images and weighted MSE. Figure 1 shows the coil-combined reference images for both T1-weighted data sets after cropping. The signal-to-noise ratio (SNR) of the acquired data (in dB) is calculated using

Figure 1.

The combined normalized reference images from data sets #1 (a) and #2 (c) are shown alongside inset regions enlarged to show detail (b, d).

$$\text{SNR}=10{log}_{10}\left(\frac{{\Vert \mathbf{x}\Vert }^2}{(\#\text{of}\text{points}\text{in}\mathbf{x}){\Vert \mathbf{\Lambda }\Vert }_{\ast }^2}\right),$$ [16]

where ||·||_* is the nuclear norm. The nuclear norm is used because each coil has a potentially different noise level, which correspond to the singular values of Λ after whitening the noise to remove correlations.

Validation of WSURE as an estimate

Using our averaged T1-weighted acquired slices as low-noise ground truths, we added complex Gaussian noise so the total noise covariance matches the covariance of a single acquisition before averaging in each instance. The synthetic noise reduces the fully-sampled SNR from 30 dB to 22 dB for the first data set, and 26 dB to 20 dB for the second. We applied the GRAPPA-based DESIGN method to uniformly 2 × 2 undersampled k-space and the L₁-SPIRiT method to 2D Poisson-disc nonuniformly undersampled Cartesian k-space (undersampling factor R ≈ 5), leaving a 24 × 24 non-undersampled block of central k-space for calibration data in both instances to train the 4 × 4-block GRAPPA and 5 × 5 SPIRiT kernels. In this and the experiments that follow, DESIGN was implemented using twenty Split-Bregman iterations and an isotropic (discrete) total variation (TV) sparsifying transform, and L₁-SPIRiT was implemented using 25 projection-onto-convex-sets (POCS) iterations with the 4-level ‘db4’ orthonormal DWT sparsifying transform (the code is publicly available at http://www.eecs.berkeley.edu/~mlustig/Software.html).

We computed WSURE values for both DESIGN and L₁-SPIRiT using the expressions in Eqs. [7] and [10] over ranges of γ known to contain the WMSE-optimal values (γ ∈ [10, 10⁴] for DESIGN and γ ∈ [10⁻⁴, 0.1] for L₁-SPIRiT) and several choices of ε (ε ∈ {10⁻⁵, 10⁻⁴, 0.001, 0.01} for both methods). The difference in ranges of γ can be ascribed to the relatively different scales of the k-space data – the implementation of L₁-SPIRiT uses the unitary FFT operator, while DESIGN uses the un-normalized FFT. These WSURE estimates were generated using the same realization of the complex random vector b, and we computed M̃GΛb just once. Also, when evaluating WSURE for the same γ and different values of ε, we reused f_γ(y). To validate WSURE as an appropriate proxy for the MSE criterion, we compared these values to the true WMSE in Eq. [3] and approximate WMSE in Eq. [4]. To gauge the precision of our estimates, we repeated our WSURE calculations for a total of twenty realizations of b to compute the sample standard deviations of these Monte Carlo estimates. To generalize our validation, we repeated these experiments for both data sets, using the same values of ε in each.

Parameter Selection for DESIGN

Using ε = 10⁻⁴ for both T1-weighted data sets, we computed the WSURE-optimized DESIGN reconstructions for uniformly 2 × 2 undersampled Cartesian k-space data with various noise levels. For the first data set, we added simulated complex Gaussian noise to the averaged multi-channel reference k-space before undersampling to produce a range of 1.2 dB to 13 dB SNR. We added noise to the second data set to yield a range of 4.6 dB to 17 dB SNR as well. We found the WSURE-optimized reconstruction using a coarse-then-fine two-level parameter sweep of γ, with the coarse level considering γ between 0.01 and 10⁶ for the first data set and between 10⁻³ and 10⁵ for the second. We compared the WSURE-optimized reconstruction against the WMSE-optimal reconstruction found using MATLAB’s fminsearch() function from a starting point of γ = 1000 for the first data set and γ = 10 for the second. This WMSE-optimal reconstruction takes advantage of the fully-sampled ground truth to avoid the x ≈ GMx approximation. We also included a comparison against an L-curve-like curvature maximization of the log-log pareto optimality curve for DESIGN, trading off ℓ_1,2 norm joint sparsity for least-squares consistency with the GRAPPA reconstruction [12]. To maximize the curvature, we used a two-level parameter sweep over the same range as for WSURE. We emphasize that this method differs from L-curve methods in that the L-curve balances the data prediction residual norm with the regularization term. Since DESIGN preserves the acquired data, the data prediction residual does not depend on γ, so the standard L-curve method cannot be applied. The un-regularized GRAPPA reconstruction was included as a baseline.

Performance of WSURE for L₁-SPIRiT

Using ε = 10⁻⁴, we studied the same performance trends for the L₁-SPIRiT reconstruction method for a range of undersampling factors on both T1-weighted data sets. We performed Poisson-disc random Cartesian undersampling for accelerations between 2 and 6, and we repeated finding the WSURE-optimized and WMSE-optimal L₁-SPIRiT reconstructions for each sampling pattern. The noise level was held fixed at 13 dB SNR and 14 dB SNR, respectively, for the two data sets (again adding synthetic complex Gaussian noise to the averaged reference k-space before undersampling). We used a coarse-to-fine two-level parameter sweep to find the WSURE-optimized γ, with the coarse level sweeping γ between 10⁻⁷ and 10 for both data sets, and we used fminsearch() with a starting point of γ = 0.01 (again for both data sets) to find the WMSE-optimal γ. We also computed the L-curve-like log-log pareto optimality curve of the SPIRiT-consistency and sparsity terms [15] and maximized its curvature using the same two-level parameter sweep for both data sets. This L-curve-like method is not a standard L-curve method for the same reason as for the DESIGN reconstruction. Un-regularized SPIRiT was provided as a baseline.

Violating the Assumption x = GMx

At high levels of acceleration, or when the coil channels do not provide sufficient spatial encoding to overcome that acceleration, the linear parallel imaging method symbolized by G does not satisfy x = GMx, even for noise-free k-space x. In such cases, our WSURE metric may not accurately reflect the true WMSE, and automatic parameter tuning may suffer. To investigate the effects of such a violation, we applied L₁-SPIRiT to the first data set at a high level of undersampling, R ≈ 6. For this undersampling factor, we repeat the validation experiment carried out earlier on the first data set, using the same range of ε and γ as before.

RESULTS

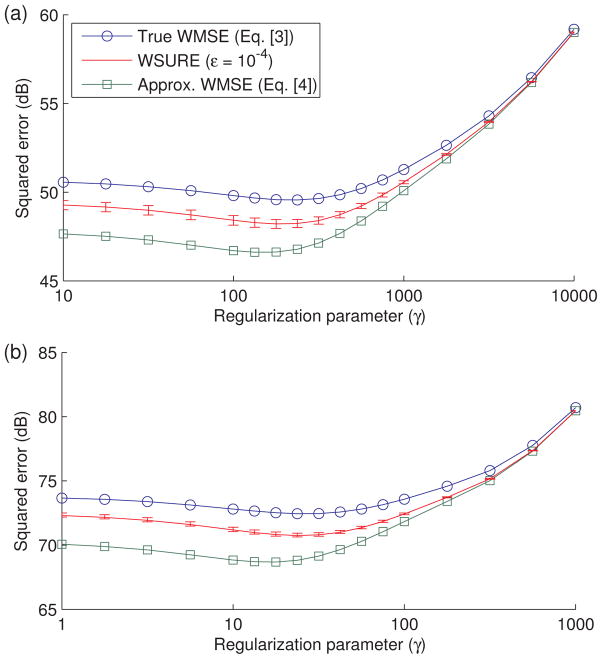
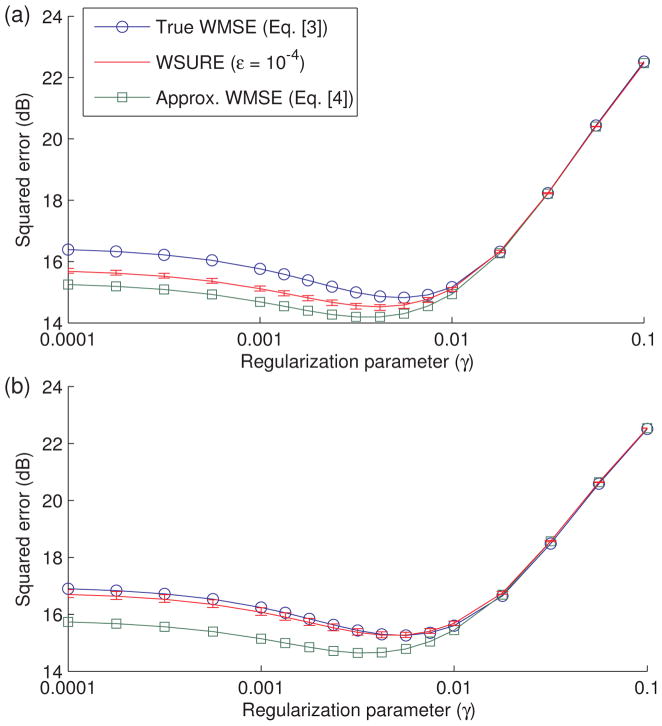
The results of our validation experiments for DESIGN and L₁-SPIRiT are illustrated for both T1-weighted data sets in Figs. 2 and 3, respectively. The value of ε shown is 10⁻⁴ for both data sets with both DESIGN and L₁-SPIRiT. The other values of ε considered yielded essentially identical curves to these curves, implying that WSURE estimates are fairly insensitive to ε for either of these nonlinear methods. For ease of comparison, the constant term in Eq. [10], which depends on the true value x, is computed from the reference k-space and added to WSURE estimates in the figures. This value is a constant offset, so it is not needed to find the WSURE-optimized γ. In both cases, the trend of WSURE estimates follows the shape of the curves for both true and approximate WMSE, although they tend to deviate more for smaller values of the regularization parameter. In addition, the approximate WMSE values are similar to the true WMSE values, validating the approximation GMx ≈ x made in Eq. [4]. In addition to having similar shapes, these curves share similar minima, validating the accuracy of our proposed WSURE error criterion. The error bars depicting ±5 sample standard deviations from the sample mean of our 20 WSURE estimates also suggest that a single realization of b is sufficiently precise to choose γ that minimizes the WMSE effectively. The maximum observed sample standard deviations were 1.2 and 0.63 percent of the mean for DESIGN and L₁-SPIRiT, respectively.

Figure 2.

WSURE for GRAPPA-based DESIGN, shown for data sets #1 (a) and #2 (b) with ε = 10⁻⁴, are similar in shape to the true weighted MSE curves and the GRAPPA-approximated weighted MSE curves and are minimized by nearly the same value of γ as the true WMSE curves in each case. The error bars on WSURE curves correspond to plus/minus five standard deviations from the mean WSURE value. Only the error bars were estimated from 20 realizations of the complex Bernoulli noise vector b; the WSURE curves correspond to using just the first realization of b. The curves are shown for 2 × 2 uniform undersampling (with a 24 × 24 fully-sampled central ACS block), with 22.3 dB input SNR for the first data set and 19.7 dB input SNR for the second.

Figure 3.

WSURE for L₁-SPIRiT, shown for data sets #1 (a) and #2 (b) with ε = 10⁻⁴, closely tracks both the true weighted MSE and the SPIRiT-approximated weighted MSE curves. WSURE curve error bars correspond to plus/minus five standard deviations from the mean WSURE value. Only the error bars were estimated from 20 realizations of the complex Bernoulli noise vector b; the WSURE curves correspond to using just the first realization of b. The curves are shown for R ≈ 5 Poisson-disc undersampling (with a 24 × 24 fully-sampled ACS region), with 22.3 dB input SNR for the first data set and 19.7 dB input SNR for the second.

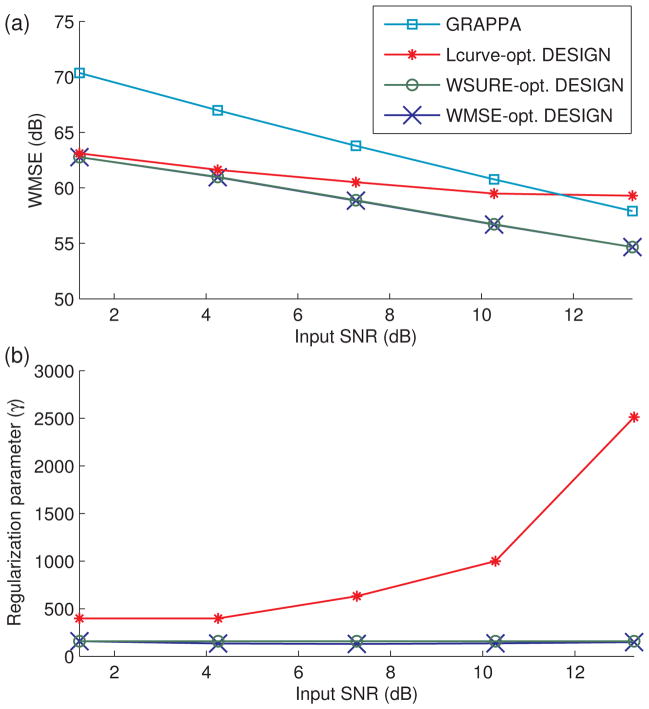
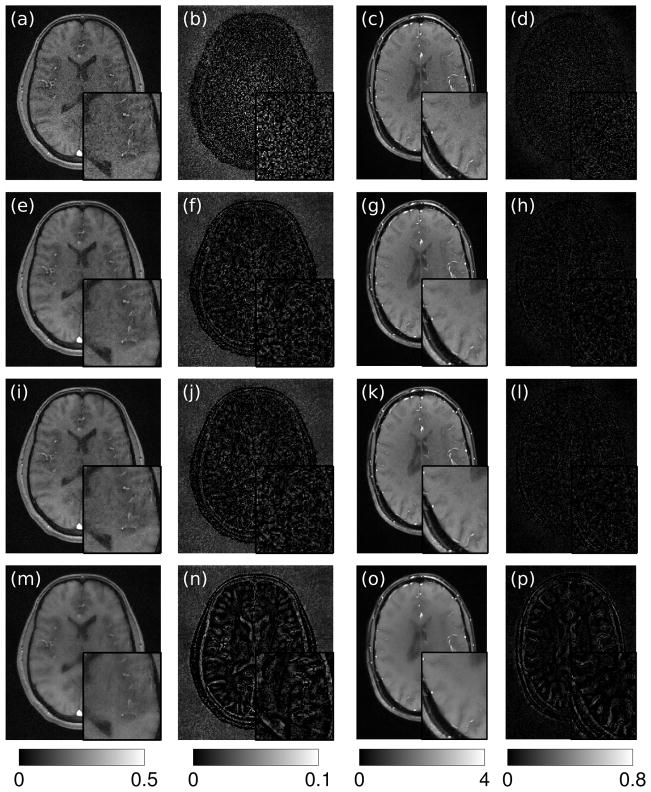
Figure 4 shows the optimal γ’s and WMSE values for the first T1-weighted data set of the WSURE-optimized and WMSE-optimal DESIGN reconstructions, for a range of noise levels, with 2 × 2 uniform Cartesian undersampling. The curves for the second data set display similar behavior and can be found online as supplementary material. The staircase-ramp effect observed in the plot of WSURE-optimized γ is due to the coarseness of the employed parameter sweep. Additional sweep levels would not be meaningful considering that the change in WMSE is so small around the minimum as to be nearly comparable to the standard deviation in the Monte Carlo WSURE estimates. The L-curve-like method maximizing the curvature of the log-log pareto optimality frontier tends to overestimate γ for both these data sets, particularly in the cases of high input SNR. For the second data set, the L-curve-selected γ does not increase monotonically, indicating difficulty in estimating the second derivative of the log-log pareto curve numerically for this application. The WMSEs of the reconstructions guided by L-curve selection suffer as a result. The multi-channel k-space WMSE values for the WMSE-optimal and WSURE-optimized choices of γ show little difference between reconstructions optimal for these error criteria, so we examine the reconstructed sum-of-squares-combined magnitude and difference images for data set #1 with 10.3 dB input SNR and data set #2 with 16.7 dB input SNR, all in Fig. 5. Both WMSE-optimal and WSURE-optimized DESIGN reconstructions display similar reduction in noise level over the GRAPPA-reconstructed image and minimal residual image structure in the difference images. Both data sets’ reconstructions for DESIGN with L-curve-selected γ portray significant oversmoothing.

Figure 4.

Varying the noise level of 2×2 uniform undersampled data, the sparsity-promoting DESIGN method yields similarly lower WMSE (a) for both WMSE-optimal and WSURE-optimized choices of γ, relative to the un-regularized GRAPPA reconstruction, for the first data set. The WMSE of the DESIGN reconstruction using the WSURE-optimized choice is within 0.038 dB of the true WMSE-optimal DESIGN reconstruction. This behavior is consistent with the WMSE-optimal and WSURE-optimized choices for the DESIGN regularization parameter γ (b) being nearly the same for this example. The L-curve-style method, however, appears to overestimate γ, yielding images with slightly higher WMSE, and in the high-SNR case, worse than performing un-regularized GRAPPA.

Figure 5.

The GRAPPA-reconstructed image (a) and difference image (b) for data set #1 with 10.3 dB input SNR display significant noise, while DESIGN with both WMSE-optimal (e,f) and WSURE-optimized (i,j) choices of γ effectively denoise the image while losing only a small amount of detail. The L-curve-based method (m,n) oversmooths the image, resulting in significant blurring artifacts. Similar results are observed for the second data set with 16.7 dB input SNR, where remaining noise in the GRAPPA reconstruction (c,d) is mitigated by DESIGN using the WMSE-optimal (g,h), WSURE-optimized (k,l), and L-curve-selected (o,p) choices of γ. Again, oversmoothing in the L-curve-based reconstruction is visible in the second data set. The difference images are displayed at 5× scale.

The results for WSURE-optimized L₁-SPIRiT yield nearly WMSE-optimal performance over a range of undersampling factors for both T1-weighted data sets. The trends in the optimal choices of γ and the resulting WMSE’s plotted in Fig. 6 for the second data set with 14 dB SNR noise nearly match the optimal performance over the entire range of acceleration. The curves for the first data set with 13 dB input SNR are similar to these curves; they can be found online as supplementary material. The same staircase-ramp effect is observed for the WSURE-optimized γ curve due to the resolution of the parameter sweep. While the L-curve-like curvature maximization of the log-log pareto optimality curve yields suboptimal γ curves for both data sets, the WMSEs appear to be much closer for L₁-SPIRiT than DESIGN. The reconstructed images in Fig. 7 confirm the numerical comparisons for the 4× undersampled case for both T1-weighted data sets, as the sum-of-squares-combined magnitude and difference images are nearly indistinguishable between the WSURE-optimized, and WMSE-optimal, and L-curve-based reconstructions. Each yields noticeable noise reduction over the un-regularized SPIRiT reconstruction shown for comparison.

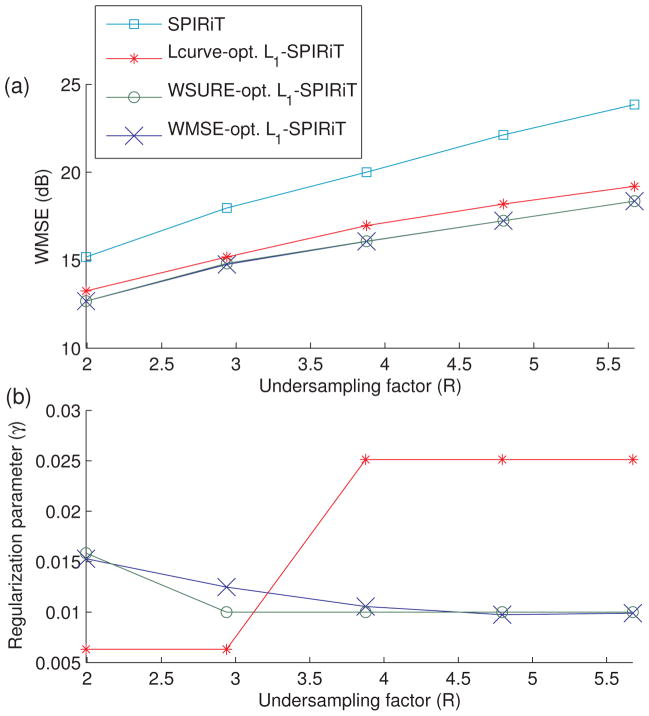
Figure 6.

The sparsity-regularized L₁-SPIRiT reconstruction for data set #2 with 14 dB input SNR yields lower WMSE (a) for both the WMSE-optimal and WSURE-optimized choices of γ, relative to the un-regularized SPIRiT reconstruction. The L₁-SPIRiT reconstruction using the WSURE-optimized choice is within 0.056 dB of the true WMSE-optimal L₁-SPIRiT reconstruction. The WMSE-optimal and WSURE-optimized choices for the L₁-SPIRiT regularization parameter γ (b) tend to decrease slowly as the undersampling factor increases. The larger values of γ from the L-curve-like method increase the WMSE, but not as substantially as for DESIGN. The plotted values of R account for the central k-space calibration region.

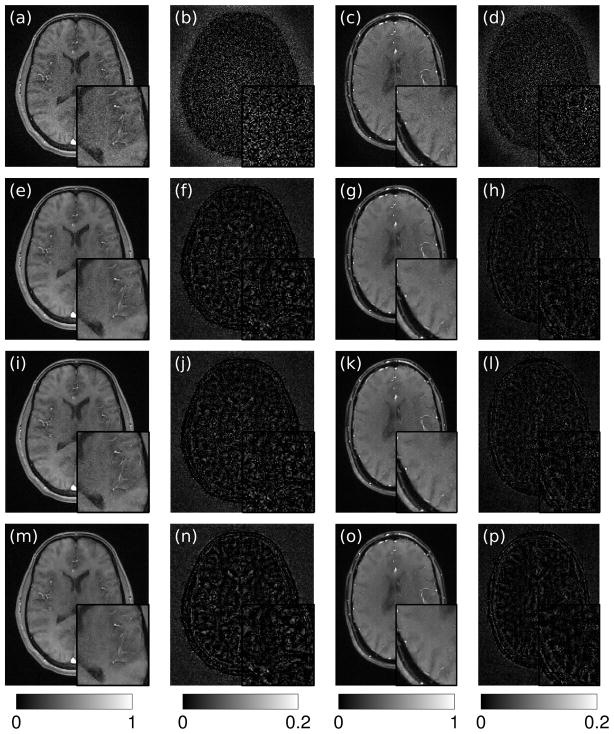
Figure 7.

The un-regularized SPIRiT reconstruction (a) and difference image (b) for data set #1 with R ≈ 4 Poisson-disc undersampling and 13 dB input SNR display significant noise, while L₁-SPIRiT with WMSE-optimal (e,f), WSURE-optimized (i,j), and L-curve-selected (m,n) choices of γ effectively improve image quality by nearly the same amount. The L-curve-based method results in a slightly oversmoothed image, although the difference is not as apparent as for the DESIGN reconstruction. Similar conclusions can be inferred from the second data set with R ≈ 4 Poisson-disc undersampling and 14 dB input SNR. The SPIRiT reconstruction (c,d) is relatively noisy, while L₁-SPIRiT with WMSE-optimal (g,h), WSURE-optimized (k,l), and L-curve-selected (o,p) choices of γ all denoise the image while avoiding substantial oversmoothing. The difference images are displayed at 5× scale.

Lastly, we investigate the effects of violating the x = GMx approximation used to form WSURE estimates. In the case of L₁-SPIRiT with the first T1-weighted data set, shown in Fig. 8, WSURE validation appears to show a breakdown in the approximation starting at R ≈ 6, but at this high level of undersampling, the image quality of even the WMSE-optimal L₁-SPIRiT reconstruction is degraded beyond the point of diagnostic utility. The WSURE-optimized choice of γ is a bit off the WMSE-optimal choice, but the additional loss of image quality appears negligible.

Figure 8.

At an acceleration of R ≈ 6, WSURE for L₁-SPIRiT, shown for data set #1 with ε = 10⁻⁴, tracks the SPIRiT-approximated weighted MSE curve when the x = GMx approximation is violated (a). However, both these curves do not follow the true MSE curve as closely as before. The resulting WSURE-optimized γ hence is slightly off, but the overall performance degradation in the WSURE-optimized image (d) is insignificant compared to the low quality of the WMSE-optimal L₁-SPIRiT reconstruction (c). The un-regularized SPIRiT reconstruction (b) is shown for reference. WSURE curve error bars correspond to plus/minus five standard deviations from the mean WSURE value. Only the error bars were estimated from 20 realizations of the complex Bernoulli noise vector b; the WSURE curves correspond to using just the first realization of b.

DISCUSSION

The experiments validate the use of Monte Carlo WSURE for regularization parameter selection for both DESIGN with uniform Cartesian and L₁-SPIRiT with nonuniform Cartesian undersampling, over a wide range of acquisition parameters including different undersampling factors and noise levels. Since the derivation of the Monte Carlo WSURE method is applicable to data-preserving reconstruction methods, and the implementation requires only the ability to evaluate the reconstruction function, this approach to parameter selection should readily generalize to other parallel imaging reconstruction algorithms. Also, the Monte Carlo WSURE can be applied to existing reconstruction methods like L₁-SPIRiT without considering the implementations of such methods. Our method requires just two evaluations of the regularized reconstruction per candidate γ. While hard-coding regularization parameters may suffice to produce high-quality images in some instances, as suggested by the relatively narrow range of WMSE-optimal γ for the presented experiments, being able to choose such parameters automatically would reduce the burden on programmers and practitioners to ensure parameter choices are indeed reasonable. This paper describes a novel way of using parallel imaging to estimate the WMSE (or MSE) with SURE for image reconstruction problems that applies to data-preserving methods. This ability to tune parameters for algorithms that preserve the acquired data sets the proposed method apart both from previous work using SURE and popular parameter selection methods like discrepancy principle, cross-validation, and L-curve curvature maximization.

In this paper, we consider uniform and nonuniform Cartesian undersampling, but our framework also can handle regularized non-Cartesian parallel imaging reconstructions and reconstructions that do not preserve the data with only minor modifications. However, in non-Cartesian parallel imaging, where the reconstructed k-space typically are located on a Cartesian grid, preserving the data makes less sense, and existing Monte Carlo SURE-based methods can be applied instead. More sophisticated cost functions that preserve edges and local details may also be compatible with the WMSE and WSURE framework.

Our experiments involved optimizing a single regularization parameter, but our SURE-based method extends to tuning multiple parameters. In the multivariate case, various minimization methods can be used (34,35). However, these methods may be more sensitive to initialization and nonconvexity of the error criterion with respect to the regularization parameters.

A limitation of the framework is the approximation GMx ≈ x that is necessary to relate the measurement locations to the full k-space; at high accelerations, this approximation becomes limited by the number and geometry of the coils (or more generally, the limitations on linear reconstruction G). We demonstrated that at the level of acceleration where this approximation becomes an issue, the quality of even the WMSE-optimal images is too low to be useful. Another limitation is the need to choose the noise scaling parameter ε. Our validation experiments indicate that choosing the absolute best ε is not critical, and that a wide range of ε would yield similar results, even for nonlinear reconstruction methods like DESIGN and L₁-SPIRiT.

CONCLUSION

We described an extension to the Monte Carlo SURE method for regularized auto-calibrating parallel imaging reconstruction methods like DESIGN and L₁-SPIRiT. We performed experiments on real data to validate WSURE estimates of the WMSE and demonstrated that the Monte Carlo WSURE estimates yield nearly WMSE-optimal reconstruction quality for both uniform undersampling with DESIGN and nonuniform Cartesian undersampling with L₁-SPIRiT. In these experiments, we also compared our method against an L-curve-like method for parameter selection that tended to oversmooth the reconstructed images. We concluded with a discussion of useful extensions and possible limitations of our method.