Depth effect on lightness revisited: The role of articulation, proximity and fields of illumination

Abstract

The coplanar ratio principle proposes that when the luminance range in an image is larger than the canonical reflectance range of 30:1, the lightness of a target surface depends on the luminance ratio between that target and its adjacent coplanar neighbor (Gilchrist, 1980). This conclusion is based on experiments in which changes in the perceived target depth produced large changes in its perceived lightness without significantly altering the observers' retinal image. Using the same paradigm, we explored how this depth effect on lightness depends on display complexity (articulation), proximity of the target to its highest coplanar luminance and spatial distribution of fields of illumination. Importantly, our experiments allowed us to test differing predictions made by the anchoring theory (Gilchrist et al., 1999), the coplanar ratio principle, as well as other models. We report three main findings, generally consistent with anchoring theory predictions: (1) Articulation can substantially increase the depth effect. (2) Target lightness depends not on the adjacent luminance but on the highest coplanar luminance, irrespective of its position relative to the target. (3) When a plane contains multiple fields of illumination, target lightness depends on the highest luminance in its field of illumination, not on the highest coplanar luminance.

1. Introduction

The perceived shade of gray of a surface, known as lightness, is a perceptual quality that corresponds to its reflectance, which is the proportion of incident light a surface reflects. Lightness perception is problematic because the light reflected from an object's surface to the eye confounds the information about surface reflectance with that about illumination intensity. Because illumination varies over time and space in natural viewing, the absolute intensity of light reflected from the surface to the eye, called luminance, may vary over a large range. Despite this variation, the visual system seems to maintain relatively constant representation of perceived surface lightness (Gilchrist, 2006; Katz, 1935). A fair degree of constancy is necessary for a system whose main goal is to represent objects and their properties, and as these objects are distributed in space, it is reasonable to assume that the perception of object properties, such as lightness, is closely related to their perceived spatial position.

A striking demonstration of the effect of depth on lightness, called the Mach bent-card illusion (Mach, 1886), has been well known. However, most of the early studies that explored the relation of lightness and perceived depth either failed to find any depth effects (Epstein, 1961; Gibbs & Lawson, 1974; Julesz, 1971; Redding & Lester, 1980) or found effects that were weak (Gogel & Mershon, 1969; Kardos, 1934), varying from 0.25 (Flock & Freedberg, 1970) to 1.25 Munsell steps (Beck, 1965). In contrast to this early work, Gilchrist (1977, 1980) obtained dramatic changes in target lightness—spanning most of the black to white range—as a function of perceived depth.

In his studies, Gilchrist used a modified version of the paradigm introduced by Hochberg and Beck (1954), in which the perceived position of the target could be varied with no significant change in the observers' retinal image. In the perpendicular-planes setup of Gilchrist's, the display consisted of two surfaces meeting at a right angle. One surface was covered with black paper and dimly illuminated, while the other was covered with white paper and brightly illuminated, producing a large overall luminance range (∼900:1). Two equiluminant trapezoidal targets extended from the corner at which the surfaces met: a white target, extending from the dimly illuminated black side, was seen against the brightly illuminated white side of the display, and a black target, extending from the brightly illuminated white side, was seen against the shadowed black side of the display.

When viewed binocularly, the display was perceived veridically in depth: each target appeared coplanar with the side of the display from which it extended. The shadowed white target appeared light gray (Munsell 8.0) and the lighted black target appeared close to black (Munsell 3.0). When viewed monocularly, however, because it was trimmed to match the linear perspective projection of a rectangle lying on the side of the display it was seen against, each target appeared coplanar with that side and its perceived lightness significantly changed. The shadowed white target, now perceived as coplanar with the lighted side of the display, appeared dark gray (Munsell 3.75), while the lighted black target, now perceived as coplanar with the shadowed side of the display, appeared light gray (Munsell 7.75). Thus, across the two viewing conditions (binocular vs. monocular), each target appeared in a different spatial position with a different coplanar neighbor; this change in perceived position was followed by a large change in perceived lightness (4.25–4.75 Munsell steps) even though the observers' retinal image was essentially the same. Based on the results of his experiments, Gilchrist formulated the coplanar ratio principle, which states that when a surface has a coplanar adjacent neighbor and the luminance range in the image is much larger than 30:1, “lightness depends on luminance ratios between adjacent retinal regions that appear to be coplanar” (Gilchrist, 1980; Gilchrist, 2006, p. 162).

1.1. Anchoring theory accounts for the effect of depth on lightness

Note, however, that the coplanar ratio principle predicts the change of target lightness only roughly—if lightness strictly depended on coplanar ratios, one would expect the target to change from black, when it appeared coplanar with a surface 30 times higher in luminance, to white, when it appeared coplanar to a surface 30 times lower in luminance. However, neither of the targets appeared totally black or totally white. In fact, the results obtained in the perpendicular-planes experiment are more closely predicted by the anchoring theory of lightness, developed later by Gilchrist et al. (1999) than by the coplanar ratio principle. We will first briefly summarize the main ideas of anchoring theory and then outline its predictions about the effect of depth on lightness.

According to anchoring theory, the visual system segregates an image into functional units for lightness computation called frameworks, which typically represent a group of surfaces that have common illumination. In segregating images into frameworks, the visual system relies on two main factors—depth boundaries and blurred boundaries (penumbrae)—but other grouping principles, such as Gestalt grouping principles, can also play a role.

Within a framework, surface lightness is computed based on anchoring rules—the highest luminance rule and scale normalization (Gilchrist, 2006; Gilchrist et al., 1999). The highest luminance rule specifies how the relative luminance values in the framework map onto the absolute lightness scale and states that the highest luminance surface within a framework (L_max) will be assigned a value of white with lower luminances scaled relative to that (Gilchrist et al., 1999; Land & McCann, 1971; Marr, 1982). Scale normalization concerns the relationship between the range of luminance values in the framework and the range of perceived reflectance values. It asserts that when the luminance range within the framework significantly deviates from the canonical 30:1 range of white to black, the visual system tends to compensate for this either through expansion of the perceived reflectance range if the luminance range is much smaller than 30:1 or through compression if it is much larger.

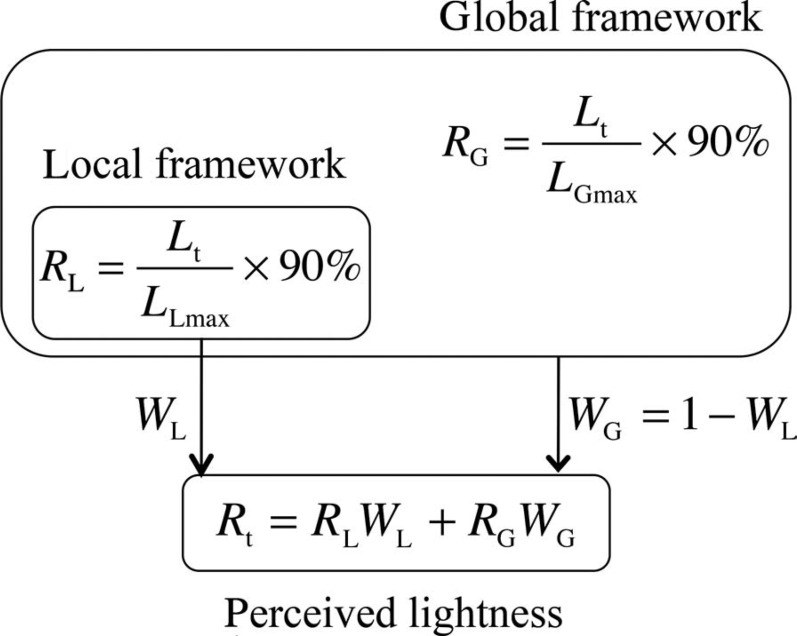
In a complex image that contains multiple frameworks, the lightness of a target surface (R_t) is the result of co-determination (Kardos, 1934). This means that it is a weighted average of target lightness computed within a local framework (R_L), which is the group of surfaces the target is immediately grouped with, and within a global framework (R_G), which is equal to the whole visual field. This co-determination is shown schematically in Figure 1. The weight of a local framework (W_L) relative to the global is determined by framework size, number of elements within the framework (articulation) and the strength of segregation (Gilchrist, 2006; Gilchrist et al., 1999).

Figure 1.

Schematic representation of lightness computation proposed by anchoring theory (Gilchrist et al., 1999). The lightness of a target surface (R_t) is a weighted average of target lightness computed within a local (R_L) and within a global (R_G) framework. The represented computation is simplified and describes the within-framework computation solely as a function of highest luminance. The local/global framework weighting (W_L vs. W_G) depends on the local framework size, articulation and its strength of segregation within the global framework.

Note that contrary to the coplanar ratio principle and lightness theories based on local contrast, anchoring theory asserts that surface lightness depends not on adjacent luminance but on the highest luminance in a framework irrespective of its position relative to the target.

In terms of anchoring theory, the planes in the perpendicular-planes setup we described represent local frameworks segregated by a depth boundary. Within each plane (local framework), target lightness is computed according to the highest luminance rule. Thus, the target will be locally assigned the value of black when it appears coplanar with the brightly illuminated white surface (the highest local luminance, L_Lmax), and locally assigned the value of white when it appears coplanar with the dimly illuminated black surface, as in this condition the target itself is the highest luminance in the local framework.

The principle of co-determination requires that global anchoring be factored in. Estimates of the global target lightness in an image with a large luminance range can be derived from the work of Radonjić, Allred, Gilchrist, and Brainard (2011), who investigated luminance-to-lightness mapping in images that had a luminance range as large as 10,000:1 but lacked cues that would allow their segmentation into local frameworks. This study showed that when faced with the challenge of mapping such a large range of surface luminance onto the much smaller range of surface reflectances, the visual system roughly maps the highest luminance to white, as predicted by the highest luminance rule. However, the visual system also exhibits remarkable compression, consistent with the scale normalization (Gilchrist, 2006; Gilchrist et al., 1999). As a result of this scaling of the luminance range, surfaces whose luminance falls near the midpoint of the image luminance range (on a log scale), like the targets in the perpendicular-planes display, are perceived as dark-to-middle gray (Munsell 3.5–5). As the luminance range and the highest luminance in the global framework in the perpendicular-planes setup remain constant across the viewing conditions, the global lightness of the targets will also remain the same.

According to anchoring theory, the large change in target lightness with the change in its perceived spatial position occurs because the local lightness value assigned to the target changes from black to white. However, the failure of the targets to appear fully white or fully black occurs because of co-determination which causes locally black target to appear dark gray and the locally white target to appear light gray.

1.2. Experiment outline

The analysis above suggests that anchoring theory may account for the effect of depth on lightness more successfully than the original coplanar ratio hypothesis. Aiming to further probe the mechanism that the visual system uses to determine surface lightness in complex three-dimensional scenes, we designed a program of experiments in which we used a variation of Gilchrist's perpendicular-planes display to test differing predictions made by anchoring theory and the coplanar ratio principle about the role of spatial and photometric factors, such as display complexity (articulation), proximity to highest coplanar luminance and spatial distribution of fields of illumination, on the depth effect on lightness. Our experiments also have implications for a number of broader questions in lightness theory, such as the debate between framework models and layer (decomposition) models (Anderson & Winawer, 2005; Gilchrist, Delman, & Jacobsen, 1983), the role of local contrast in lightness computation in complex three-dimensional displays, and the relationship of spatial filtering models (Blakeslee & McCourt, 2004) and the effects of depth on lightness.

In Experiment 1, we tested the role of articulation by comparing the size of the depth effect when the sides of our perpendicular-planes display were homogeneous versus when they were richly articulated using Mondrian patterns. In Experiment 2, we tested specific anchoring theory predictions about the asymmetric effect of articulation in the shadowed and lighted planes. In Experiment 3, we asked whether the depth effect on lightness depends on adjacent or on the highest coplanar luminance. Finally, in Experiment 4, we varied the spatial distribution of fields of illumination in the image to address the following question: when a plane contains multiple fields of illumination, does the target lightness depend on the highest luminance in the plane or the highest luminance in the framework of illumination?

2. General methods

2.1. Apparatus

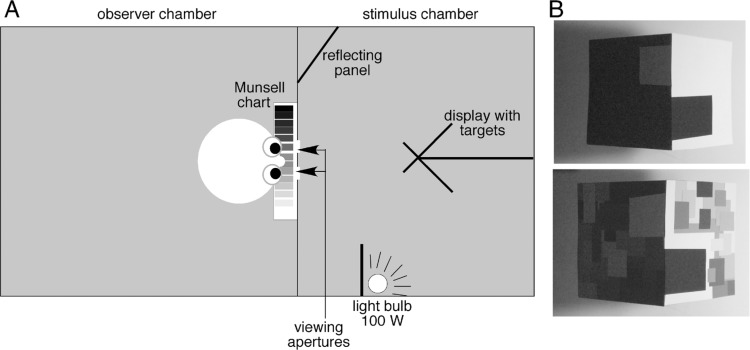
The experiments were set in a vision tunnel (117 cm × 60 cm × 60 cm; Figure 2A), which consisted of a stimulus chamber (51 cm long) and an observer chamber (66 cm long). The observer, sitting in the observer chamber, viewed the experimental scene through apertures centered in the wall dividing the two chambers. In the binocular viewing condition, the observers viewed the display through two round apertures (ϕ 3 cm). In the monocular condition, the observers looked through a pinhole (ϕ 3 mm), centered within the right aperture while occluding panel covered the left aperture. The floor and right sidewall of the stimulus chamber were covered with gray Color-aid paper (reflectance 24.6%), the back wall was covered with matte white paper (reflectance 90%), and the left sidewall, ceiling and front wall were painted matte black.

Figure 2.

(A) Plan view of the experimental apparatus (drawn to scale). (B) Photographs of the display in the low- (top) and high- (bottom) articulation conditions used in Experiment 1 (taken only approximately from the observer's viewpoint and thus showing here a somewhat distorted perspective).

2.2. Perpendicular-planes display

Looking straight ahead through the apertures, the observer saw what appeared to be two sides of a large cube suspended in midair, 23.5 cm above the floor. Two visible sides of the “cube” met at a vertical right angle pointing toward the observer. Each side was 11 cm and constructed from color-aid paper. These paper sides were mounted on a support apparatus consisting of two square aluminum panels, which formed a dihedral corner. The display was supported by a 16-cm-long aluminum rod, which extended from the center of the back wall of the tunnel and was occluded by the display itself. Two square Color-aid paper targets (approximately 4.5 × 4 cm) extended from the corner of the display. For rigidity, each target was glued to a thin metal panel. As in the original display of Gilchrist, the white target (the lower target; reflectance 90%) extended from the shadowed plane and was seen against the lighted plane of the display. The black target (the upper target; reflectance 3.1%) extended from the lighted plane and was seen against the shadowed plane of the display. Although each target physically lay in one plane, each was cut in a slightly trapezoidal shape so that its linear perspective was consistent with its orthogonal plane. Thus, when viewed monocularly through the pinhole, each target appeared to lie in that plane.

2.3. Illumination

The scene was illuminated by a 100-W incandescent bulb attached to the right wall of the stimulus chamber, 30 cm away from the display and occluded from the observer's view by an aluminum panel (16.5 cm × 17.5 cm). The bulb directly illuminated the right plane of the display and the upper black target extending from it, while the left plane and the lower white target were in dim illumination.

The illumination ratio between the right and left planes was approximately 30:1 and chosen so that the luminance values of the black and white targets (reflectance ratio of 1:30) were roughly equal under these illumination conditions. Precise equation of target luminance was achieved by mounting a reflecting panel (white paper on a black background) in the front left corner of the stimulus chamber, parallel to the shadowed plane of the display and out of the observer's view (Figure 2A). By varying the size of the white paper, we could control the amount of light reflected onto the white target and adjust its luminance with precision.

2.4. Proximal stimulus

At the viewing distance of 42 cm, the visual angle of the display was 15° vertically and 20.2° horizontally. The visual angle of the targets was approximately 6.2° horizontally and 4.8°–5.5° vertically.

2.5. Matching chart

The observers made lightness matches using a Munsell chart consisting of 16 chips (1 × 3 cm) mounted on the white background and arranged in ascending reflectance order from Munsell N 2.0/ (black; nominal reflectance 3.1%) to Munsell N 9.5/(white; nominal reflectance 90%; measured luminance 360 cd/m²). The chart was housed in a metal chamber mounted 48 cm directly below the viewing apertures. It was separately illuminated by a 15-W fluorescent tube mounted 10 cm above the chart.

2.6. Instructions

At the beginning of the experimental session, the observers were first familiarized with the concepts of lightness and brightness through several demonstrations and introduced to the Munsell chart, then given instructions explaining the task. The full text of these instructions is available at http://nwkpsych.rutgers.edu/~alan/dlinstructions). Briefly, each observer was seated in the observer chamber and asked to look into the tunnel through the apertures. The observer was first asked questions to establish the perceived position of the targets and then asked to “to pick a chip from the chart that is the same actual color as the target; that is, cut from the same piece of paper as the target.” To further ensure that they saw the target in the intended perceived position, after making lightness matches, all observers in the monocular viewing condition were asked if the targets appeared to be lying flat on the sides of the cube. Their surprise during the debriefing, when the actual position and reflectance of the targets was revealed, further confirmed that our manipulation of perceived target position was successful.

2.7. Observers

A different group of observers judged the lightness of the two targets in each experimental condition. Within a condition, the order in which the targets were judged (upper first vs. lower first) was counterbalanced across observers. All experimental procedures were approved by institutional review board of Rutgers University and were in accordance with the World Medical Association Helsinki Declaration (October 2008).

In all experiments, the data from an observer were identified as outlying and excluded from further analysis if the matches fell more than three standard deviations above or below the mean of the whole group in a given condition (computed in Munsell values with the match of the potential outlier excluded). We introduced this exclusion criterion to diagnose observers who did not understand or follow instructions or who failed to perceive the targets in their intended spatial arrangement. Each excluded observer was replaced by a new one, so that the valid data from 20 observers were collected in each condition. The exceptions are binocular viewing of low-articulation condition of Experiment 1, in which we collected data from 23 observers, and Experiment 4, in which we collected data for 15 observers in each condition. The number of excluded observers in all four experiments was 8 (out of 211). Two were excluded from high-articulation monocular condition (Experiment 1) and one from each of the following conditions: low-articulation binocular (Experiment 1), articulation-spotlight and articulation-shadow (Experiment 2), shadow monocular, spotlight monocular and spotlight binocular (Experiment 4).

3. Experiment 1: Role of articulation in the depth effect on lightness

In the context of lightness research, “articulation” generally refers to stimulus complexity, although this complexity can be manifold, potentially encompassing the number of different shades of gray, surfaces and objects, illumination regions or depth planes (Gilchrist, 2006; Henneman, 1935; Maloney & Schirillo, 2002). In our study, we define articulation as the number of different surfaces within a framework. This understanding of articulation was also shared by Katz (1935), who first introduced the term and reported that greater articulation within a region of illumination leads to a higher degree of lightness constancy (Annan & Gilchrist, 2004; Arend & Goldstein, 1987; Burzlaff, 1931; Gilchrist et al., 1999; Henneman, 1935; Lotto & Purves, 1999). The exact mechanism via which articulation influences lightness processing is not known. Although the hypothesis that articulation increases constancy is widespread (Maloney & Schirillo, 2002), evidence suggests that, under certain conditions, articulation decreases constancy and increases the strength of lightness illusions (Adelson, 2000; Economou, Annan, & Gilchrist, 1998; Gilchrist & Annan, 2002; Wishart, Frisby, & Buckley, 1997).

Anchoring theory integrates these apparently contradictory findings by proposing that articulation affects lightness by increasing the strength of the local framework, and thus the weight the local framework has in lightness computation. When the frameworks correspond to fields of illumination, as in perpendicular-planes display, articulation will increase constancy, just as Katz observed. When the frameworks are formed based on grouping principles but do not correspond to fields of illumination, as in simultaneous lightness contrast, constancy will decrease as articulation increases.

Anchoring theory therefore predicts that increasing the number of elements in the planes of the perpendicular-planes display should affect the lightness of the trapezoidal targets by increasing the weight of their local framework in lightness computation. Consequently, higher articulation should lead to a larger depth effect.

In addition, anchoring theory predicts that articulation should have a larger effect on lightness of the target coplanar with the shadowed plane. This is because the difference between the locally and globally assigned lightness values is larger for this target (R_L = white, R_G = mid-to-dark gray) and, as the articulation of the shadowed plane increases, it should appear lighter. The increase in articulation should have a smaller effect on lightness of the target coplanar with the lighted plane, for which the difference between the locally and globally assigned lightness values is smaller (R_L = black, R_G = mid-to-dark gray).

In contrast, the coplanar ratio principle and the decomposition models, which make no provision for articulation, predict no change in target lightness and the depth effect with the increase in display articulation.

To test the role of articulation, we measured the depth effect on lightness when the sides of the display were homogeneous (the low-articulation condition) and when they were covered with Mondrian patterns (the high-articulation condition).

3.1. Stimulus description

In the low-articulation condition, just as in the original study of Gilchrist, the left side of the display was covered with black while the right side was covered with white Color-aid paper (reflectance 3.1% and 90%, respectively).

In the high-articulation condition, the sides of the display were covered with Mondrian patterns, each consisting of 20 patches of different reflectance ranging from black to white. The structure of the pattern was pseudorandom and approximately the same for both planes. To keep the local contrast constant across the articulation conditions, the position of the white patch in the lighted plane was kept retinally adjacent to both targets, just as in the low-articulation condition. The position of the black patch in the shadowed plane was slightly changed so that although most of the retinal surround of the targets was black, some lighter patches were adjacent to both targets. Their reflectance was kept relatively low to minimize the change in average local luminance. Note that any local contrast effect due to this change would result in darkening of the upper target, retinally surrounded by the shadowed plane on three sides, which is opposite from the articulation effect predicted by anchoring theory.

Luminance was measured using a Konica Minolta LS-100 luminance meter (measuring error estimated from repeated measures up to 4%). In both the low- and the high-articulation conditions, the luminance of both targets was 17.7 cd/m². The two targets were the highest luminance in the shadowed plane and the lowest luminance in the lighted plane. The highest luminance patch in the lighted plane (552 cd/m²), the lowest luminance patch in the shadowed plane (0.6 cd/m²) and the overall luminance range (∼900:1) were roughly the same in the low- and high-articulation conditions. In both conditions, the luminance of the background wall varied from 525 cd/m² (on the right) to 242 cd/m² (on the left). Due to photometer unreliability at low luminance levels, reported luminance of the lowest luminance patch in the shadow is an estimate obtained by measuring the luminance of the white surface at the same position and dividing it by the reflectance ratio of the white and black paper.

3.2. Results and discussion

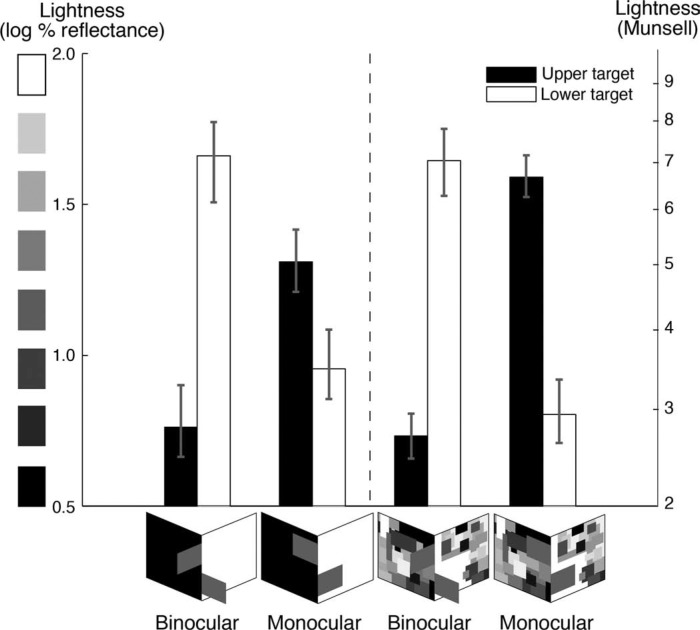
The mean lightness matches for each target in the monocular and binocular viewing of the low- and high-articulation conditions are shown in Figure 3. For purposes of data analysis, all Munsell matches are converted into log% reflectance (base 10). We provide Munsell values only as orientation for readers more familiar with the Munsell scale. Unless specified otherwise, throughout the discussion of the results we use the term coplanar to refer to perceived coplanarity (e.g. “target coplanar with …” means “target that appears coplanar with …”).

Figure 3.

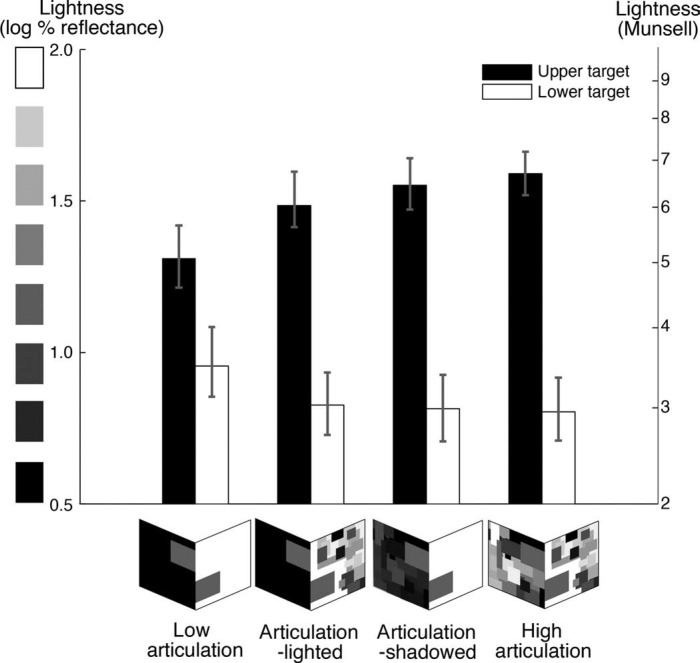
Experiment 1. Target lightness for monocular and binocular viewing in the low- and high-articulation conditions (left and right of the dashed line, respectively). Errors bars represent bootstrapped 95% confidence intervals. The x-axis depicts a perspective view of display articulation and perceived spatial arrangement (not the observer's retinal image) across conditions. For each viewing/articulation condition, lightness of the upper, lighted black target is shown in black. Lightness of the lower, shadowed white target is shown in white.

For each target and condition, we evaluated the reliability of the mean lightness matches via the bootstrap procedure (Efron & Tibshirani, 1993). We randomly sampled with replacement 20 matches from the set of actual target matches and computed the mean lightness for each target in each condition from the resampled data. In all figures, the error bars show bootstrapped 95% confidence intervals obtained over 2,000 iterations of the resampling (Efron & Tibshirani, 1993, pp. 178–201).

A two-way analysis of variance (ANOVA) with display articulation (low vs. high) and viewing condition (binocular vs. monocular) as the between-subject factors and target (upper vs. lower) as a within-subject factor revealed a target × viewing condition × display articulation interaction, F(1, 79) = 6.19, p < 0.05. We further explored this interaction by conducting two one-way ANOVAs, one for each level of display articulation, combined with planned comparisons.

In both the low- and high-articulation conditions, we replicated the basic depth effect on lightness. Target lightness significantly decreased when its perceived position changed from coplanar with the shadowed to coplanar with the lighted plane across the viewing conditions (low articulation: t(41) = 6.67 for the upper and t(41) = 7.81 for the lower target; high articulation: t(38) = 15.62 for the upper and t(38) = 10.65 for the lower target; all p < 0.001; target × viewing condition interaction in the low- and the high-articulation conditions: F(1, 41) = 76.50 and F(1, 38) = 264.00, both p < 0.001).

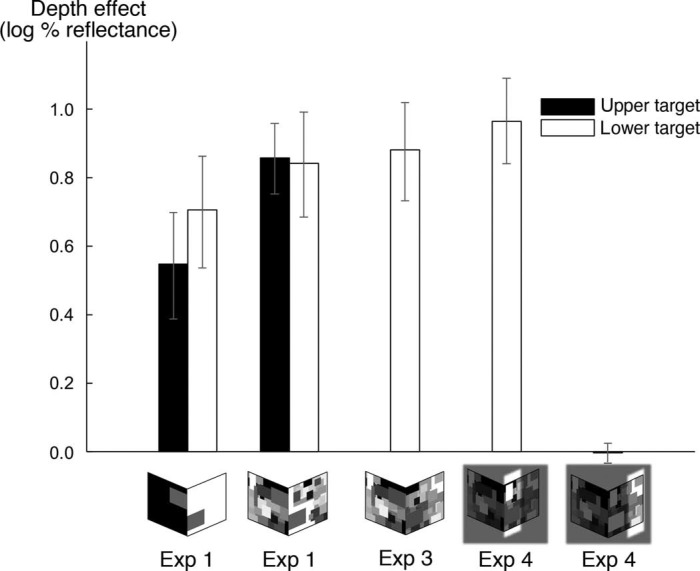
For a given target and level of display articulation, the depth effect is equal to the difference in target lightness as its perceived spatial position changes across viewing conditions—from coplanar with the shadowed plane to coplanar with the lighted plane. Central to our hypothesis, we find that increasing articulation increased the depth effect, but only for the upper (2.3 vs. 4.0 Munsell steps) and not the lower target (3.9 vs. 4.2 Munsell steps; see also Figure 8). To understand this finding better, we analyzed the change in lightness for each target as its perceived position changed across viewing conditions for the two levels of display articulation.

Figure 8.

Changes in the depth effect on lightness as a function of articulation, proximity to highest luminance and distribution of fields of illumination. Errors bars represent bootstrapped 95% confidence intervals. The depth effect is plotted in white for the lower target and in black for the upper target. Icons along the x-axis illustrate the experimental condition. The figure illustrates three main findings: (1) The depth effect increases with an increase in articulation, but only for the upper target (two leftmost pairs of bars; Experiment 1); (2) The depth effect does not change when the position of the coplanar highest luminance relative to the target is varied (the second vs. third white bar from the left; Experiments 1 vs. 3); (3) The change in the highest luminance in the target's perceived field of illumination is necessary for depth to have an effect on lightness (two rightmost white bars, Experiment 4).

Consistent with the prediction of anchoring theory, increasing articulation had no significant effect on the lightness of the target coplanar with the lighted plane (upper target in the binocular viewing; lower target in the monocular viewing). For the target coplanar with the shadowed plane, however, increasing articulation increased lightness only for the upper target in the monocular condition. The lower target in the binocular condition did not change, possibly because there was not much room for this target to lighten. According to anchoring theory, this target should appear slightly darker than white due to co-determination (Kardos, 1934): even though its lightness is mostly determined within its local framework (plane), there is always some influence of the global framework.

However, there was plenty of room for the upper target in the monocular viewing to lighten, as it appeared middle gray in the low-articulation condition. Consistent with the predictions of anchoring theory, this target appeared significantly lighter when the planes in the display were richly articulated (Munsell 5.2 vs. 6.8; t(38) = 4.22, p < 0.001).

As with the earlier experiments by Gilchrist, we found that coplanar ratios won hands down over retinal ratios. However, that does not mean that retinal ratios play no role at all. Had retinal ratios played a notable role in our experiment, this would have made the lower target in the monocular condition (embedded in the high-luminance retinal surround) darker than the upper target in the binocular condition (retinally surrounded by the dark background). However, our results go strongly in the opposite direction. While this does not prove that there was no retinal ratio effect, any such effect for our stimulus is likely to be quite small.

Our finding that articulation of the planes significantly increases the depth effect is consistent with the findings of Schirillo and Arend (1995), who obtained larger depth effects when using the richly articulated version of Gilchrist's parallel-planes display than Schirillo, Reeves, and Arend (1990), who used a poorly articulated version of the same display. Our findings also agree with those of Wishart et al. (1997), who showed that the illusory lightness difference between two patches that lie in different planes in Adelson's corrugated Mondrian illusion practically disappears when the planes are not richly articulated and consist of only one or two surfaces of different shade of gray.

4. Experiment 2: The source of the articulation effect

In Experiment 2, we tested the specific prediction of anchoring theory that the increase in the depth effect due to articulation is primarily caused by the increase in articulation of the shadowed plane. We showed in Experiment 1 that, consistent with anchoring theory predictions, increasing display articulation affected lightness only for the target coplanar with the shadowed plane, but not for the target coplanar with the lighted plane. Recall that anchoring theory proposes that varying articulation of a local framework should only affect the lightness of surfaces within that framework. Thus, the brightening of the shadowed target should be caused exclusively by increased articulation of the shadowed plane, while articulating the lighted plane should have no effect.

We tested this prediction by measuring the target lightness when only the shadowed or only the lighted plane of the display had high articulation. In the articulation-lighted condition, the lighted plane was covered with the Mondrian pattern, while black Color-aid paper covered the shadowed plane. In the articulation-shadowed condition, the shadowed plane was covered with the Mondrian pattern, while white Color-aid paper covered the lighted plane. The Mondrian patterns were identical to those used for a given plane in the high-articulation condition of Experiment 1. The luminance values for the targets and the sides of the display closely matched those in Experiment 1 (±4%). Because articulation affected lightness only under monocular viewing in Experiment 1, observers only viewed the display monocularly in Experiment 2.

4.1. Results and discussion

Mean lightness matches for each target in the articulation-shadow and articulation-spotlight conditions are plotted in Figure 4. The results from the monocular viewing of Experiment 1, when the articulation was either high or low for both planes of the display, are shown for comparison.

Figure 4.

Experiment 2. Target lightness in the articulation-lighted and articulation-shadowed conditions. The low- and high-articulation conditions from Experiment 1 (monocular viewing) are plotted for comparison. The figure follows the same conventions of data presentation as in Figure 3.

Consistent with the depth effect observed in Experiment 1, for all levels of display articulation, the lower target coplanar with the lighted plane appeared darker than the upper target coplanar with the shadowed plane (articulation-lighted t(19) = 8.55; articulation-shadowed t(19) = 8.87; main effect of target, F(3, 76) = 256.83, all p < 0.001, as shown by a two-way ANOVA with the target as a within-subjects factor and the display articulation as a between-subjects factor).

Furthermore, we find that in line with the predictions of anchoring theory, increasing articulation of either plane did not have a significant effect on lightness of the lower target (main effect of display articulation on lower target, F(3, 76) = 1.59, ns). However, contrary to anchoring theory predictions, the upper target appeared lighter with increased articulation of either plane (target × condition interaction, F(3, 76) = 5.98, p = 0.001; main effect of display articulation on the upper target, F(3, 76) = 7.20, p < 0.001). This target appeared significantly darker in the low-articulation condition than any high-articulation condition (Tukey HSD: articulation-spotlight p < 0.05; articulation-shadow p < 0.01; high articulation of both planes p < 0.001), but did not change significantly across any of the three high-articulation conditions.

In other words, we find no evidence that increasing articulation of the shadowed plane has a larger effect on target lightness (and the depth effect) than increasing articulation of the lighted plane. This is consistent with the findings of Bressan and Actis-Grosso (2006), who showed that when the local highest luminance is held constant, increasing the articulation of either of the inducing backgrounds of the simultaneous contrast display causes the target on the darker background to lighten, but does not affect the target on the lighter background.

It is possible that articulating either of the planes increases the weight of both planes by reducing their similarity and increasing their segregation from each other. This effect shows up primarily in the shadowed plane, as predicted by anchoring theory.

5. Experiment 3: The role of proximity of the highest luminance surface in the effect of depth on lightness

According to the coplanar ratio principle (Gilchrist, 1977, 1980), target lightness depends on the coplanar luminance that is retinally adjacent. To the extent to which it emphasizes local luminance ratios, this view is similar to low-level theories that predict changes in surface lightness as a function of local contrast (Cornsweet, 1970; Jameson & Hurvich, 1964; Reid & Shapley, 1988). According to anchoring theory (Gilchrist et al., 1999), however, retinal adjacency does not play a critical role in lightness computation. Instead, lightness is a function of the highest luminance in the framework to which the surface belongs. When the local framework is equivalent to a plane, as in our display, anchoring theory asserts that the lightness of a target surface depends on the highest luminance in the plane, regardless of its position relative to the target.

In Experiment 3, we tested whether lightness depends on adjacent or the highest coplanar luminance by varying the position of the highest luminance patch in the lighted plane relative to the lower target. If lightness depends on the adjacent luminance, then moving the highest luminance patch to a remote position in a plane and surrounding the target with low luminance patches should cause the target to lighten. Consequently, the depth effect on lightness should be smaller. However, if lightness depends on the highest coplanar luminance irrespective of its position in the plane, then the target lightness and the depth effect should not change as the position of the highest luminance relative to the target is varied.

In the remote condition, the Mondrian pattern for the lighted plane consisted of 20 patches of different reflectance (from white to black) distributed so that the highest luminance patch (reflectance 90%) was at a remote position relative to the target (upper right corner; see display icon in Figure 5), while patches adjacent to the target varied from dark to middle gray (reflectance 9%–22%). The distribution of the remaining patches was biased, so that the patches of lower reflectance were nearer and the patches of higher reflectance were farther from the target.

Figure 5.

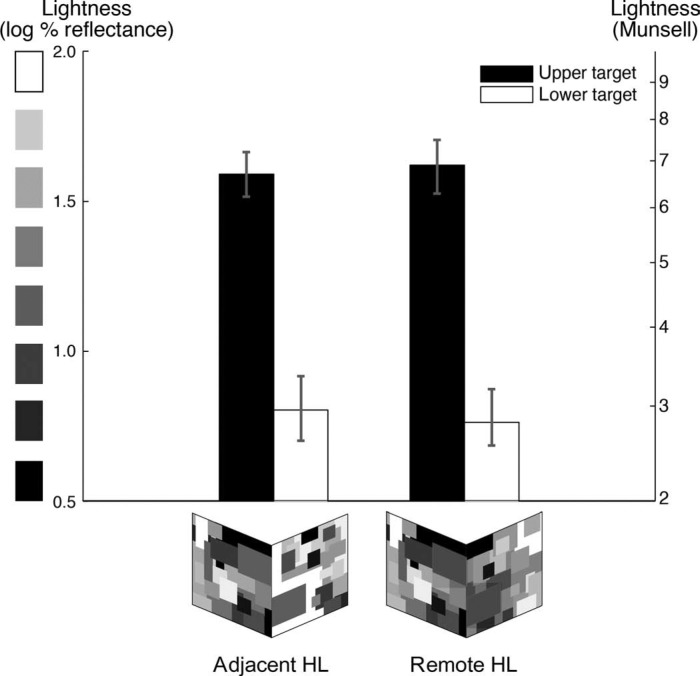
Experiment 3. Target lightness when the highest luminance is adjacent and when it is remote relative to the lower target. The adjacent condition is identical to the high-articulation condition (Experiment 1; monocular viewing). The figure follows the same conventions of data presentation as in Figure 3.

The Mondrian pattern in the shadowed plane was identical to that used in the high-articulation condition of Experiment 1 and the luminance measures were approximately the same as in that condition (targets 17 cd/m²; 90% reflectance patches in the shadowed plane and lighted plane: 14.3 and 540 cd/m²).

By varying the Mondrian pattern of the lighted plane, we changed the retinal surround of the upper target only at one (corner) edge while leaving its coplanar surround unchanged. Thus, the lightness of this target should remain roughly constant across conditions.

We measured the change in lower target lightness only for monocular viewing. In binocular viewing, this target is coplanar with the shadowed plane and is itself the highest luminance patch in its plane. Observers' matches in the remote condition were compared with those we obtained in the high-articulation condition (Experiment 1, monocular viewing), in which the highest luminance was immediately adjacent to the lower target (the adjacent condition).

5.1. Results and discussion

Figure 5 shows mean lightness matches for each target in the remote and the adjacent conditions.

Consistent with our results in Experiments 1 and 2, we found that in the remote condition the upper target appeared lighter than the lower, t(19) = 13.14, p < 0.001. Centrally to our hypothesis, however, we did not find a difference in the lightness of either target when we varied the proximity of the highest luminance patch relative to the lower target (target × proximity interaction F < 1, ns; as shown by a two-way ANOVA with target as a within-subjects and proximity of highest luminance as a between-subjects factor). Consequently, the depth effect for the lower target (computed relative to its lightness in the binocular viewing of the high-articulation condition in Experiment 1) did not significantly differ between adjacent and remote conditions (0.84 vs. 0.88 log% reflectance, 4.2 vs. 4.4 Munsell steps, respectively).

These results therefore clearly support the anchoring theory prediction that varying position of the highest luminance in the plane relative to the target does not affect target lightness. As long as the coplanar highest luminance does not change, the perceived target lightness remains the same irrespective of the position of the highest luminance patch relative to the target.

These results are consistent with the results of Cataliotti and Gilchrist (1995), who found that when a row of five gray squares of different reflectance, varying from black to white, was presented within a spotlight, the lightness of the black square did not depend significantly on its position relative to the white square (the highest luminance) in the row. Cataliotti and Gilchrist (1995) found analogous results using a Mondrian world paradigm: when looking into a trapezoidal chamber whose walls were completely covered with a grayscale Mondrian pattern that filled the observer's entire visual field, lightness matches for a set of target surfaces did not change significantly when their position relative to the highest luminance patches was varied from adjacent to remote. It may well be that position relative to the highest luminance does have an effect, albeit a weak effect and one that did not reach significance in either our study or the Cataliotti and Gilchrist study.

Our results, however, are in conflict with those of Allred and Brainard (2009), who found that varying retinal surround of the target embedded in the Mondrian pattern in the relatively complex three-dimensional scene affects target lightness, even when the highest luminance in the Mondrian is kept constant. Unlike in our study, their target was an increment and completely embedded in its local surround. In addition, the target and its surround were separated from the rest of the Mondrian by a thin black border, which may have caused the surfaces within a border to be processed as a separate local framework. Some combination of these stimulus differences may account for the different results from the two studies.

Our findings challenge not only the coplanar ratio principle but also the low-level lightness models that emphasize the importance of local contrast and predict that a change in local luminance ratios (either retinal or coplanar) will always cause a change in lightness (Cornsweet, 1970; Jameson & Hurvich, 1964; Reid & Shapley, 1988). Our results instead favor anchoring theory, which incorporates and expands the main idea of the coplanar ratio principle by asserting the dependence of target lightness not on the adjacent but on the highest luminance within a (depth) framework.

The proposition that the lightness of any surface is computed relative to the highest luminance within a group of surfaces (a depth plane, a field of illumination or the entire visual field) implies that the visual system can compare luminance ratios not only between adjacent surfaces (Wallach, 1948) but also between any two surfaces within an image, perhaps by successively integrating luminance ratios at all edges encountered along a provisional path between the two surfaces (Gilchrist et al., 1983; Land & McCann, 1971). Although the exact mechanism is not known (for proposed mechanisms see Bergstrom, 1977; Land & McCann, 1971; Rudd, 2010; Rudd & Zemach, 2004), the physiological evidence suggests that the integration is carried out by spatial filtering (Blakeslee & McCourt, 2004; Kingdom & Moulden, 1992; Shapiro & Lu, 2011).

6. Experiment 4: Does target lightness depend on the highest luminance within a plane or the highest luminance within a field of illumination?

While planes are central to the coplanar ratio principle, anchoring theory speaks instead of frameworks, which typically represent a group of surfaces under common illumination. In all the experiments we have reported up to this point, these closely related concepts coincided, as the frameworks in the perpendicular-planes display are defined by depth boundaries. However, according to anchoring theory, shadow boundaries (penumbrae) represent another major factor segregating the image into separate frameworks—and it is often the case that a single plane is not uniformly illuminated.

Therefore, we asked how lightness is computed within a plane that contains multiple fields of illumination. In Experiment 3, we established that target lightness depends on the highest luminance in the plane, but does this dependence hold in a multi-lit plane? According to anchoring theory, introducing the penumbra into the plane would cause the perceptual reorganization of frameworks in the image. The immediate local framework that the target belongs to becomes its field of illumination and its local lightness value will be computed relative to the highest luminance within this field.

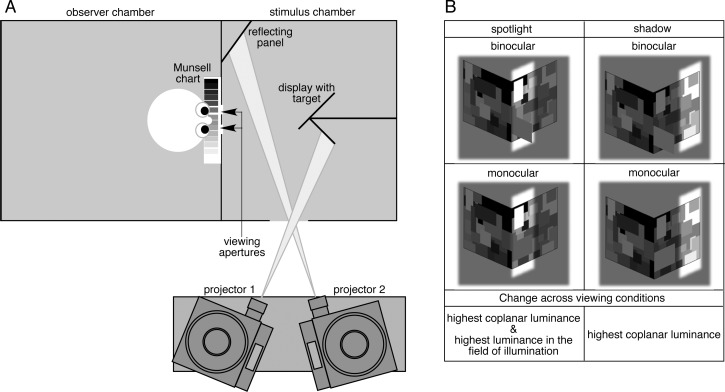
To address the question whether target lightness in a multi-lit plane depends on the highest coplanar luminance or highest luminance in the target's field of illumination, in Experiment 4 we modified the illumination conditions in the perpendicular-planes display so that one half of the right (lighted) plane was still brightly illuminated, but the other half was in shadow. Thus, the right plane now consisted of two frameworks of illumination, segregated by the penumbra, each having a different highest luminance. The display contained only the lower target, extending from the shadowed (left) plane.

In one condition (the shadow condition), the spotlight covered only the right half of the right plane so that in the monocular viewing—just as in the binocular, when it was coplanar with the homogeneously illuminated shadowed plane—the target appeared to lie in the shadow (Figure 6B). In this condition, the highest luminance in the target's local framework of illumination remained the same across the viewing conditions (and equal to target luminance). In the other condition (the spotlight condition), the spotlight covered the left half of the right plane, so that when viewed monocularly the target appeared to lie in the spotlight. Thus, in the spotlight condition, the highest luminance in the target's framework of illumination in the monocular viewing was 30 times higher than that in the binocular viewing (Figure 6B).

Figure 6.

Experiment 4. (A) Plan view of the experimental apparatus (in the shadow condition). (B) A perspective view that illustrates the perceived spatial arrangement and distribution of fields of illumination with the summary of changes in the local highest luminance across viewing conditions.

If lightness depends on the highest luminance in the plane, then the target should appear significantly darker in the monocular than in the binocular viewing, irrespective of the field of illumination to which it appears to belong in the monocular viewing. This is because in both the shadow and the spotlight conditions, the change in perceived target position is accompanied by a change in highest coplanar luminance. However, if lightness depends on the highest luminance in the framework of illumination, the target will darken in the monocular viewing only when it is in the spotlight, because only in this condition does the highest luminance in the target's framework of illumination change across viewing conditions.

6.1. Stimulus description

The experimental setup in Experiment 4 was identical to that in Experiment 3 in all respects except (1) the display contained only the lower target (white Color-aid paper, reflectance 90%) extending from the shadowed plane; (2) the illumination of the right side of the display was not uniform; and (3) a small white patch was added to the top left in the Mondrian pattern in the right plane so that in the monocular viewing the highest luminance within the spotlight remained the same, regardless of the spotlight location.

6.1.1. Illumination conditions

The display was illuminated by two projectors mounted on a stand positioned approximately 50 cm outside the tunnel right wall at a 113-cm height (Figure 6A). The beams of both projectors passed through a square aperture in the right wall of the tunnel. One projector (Kodak Carousel, model 800H with Raynox 100 mm–150 mm f3.5 zoom lens) illuminated one half of the right plane of the display. The size and shape of the illuminated field were defined by a square aperture within a metal slide inserted into the slide projector. A neutral density filter (transmittance 70%) covered the aperture to reduce the light intensity and achieve the desired luminance values. Another projector (Kodak Ektagraphic model B-2, with Kodak Ektanar C 102 mm f2.8 lens) illuminated the reflecting panel in the front left corner of the stimulus chamber and served to adjust the target luminance. To eliminate a yellow tinge in the light coming from this projector, a piece of blue paper was added to the panel.

6.1.2. Proximal stimulus

Although the absolute level of illumination in the stimulus chamber increased by a factor of ∼1.6, the relative luminance values remained the same as in Experiment 3 (target: 29.6 cd/m²; 90% reflectance patch in the spotlight: 870 cd/m², 90% reflectance patch in the shadow, both in the left plane and shadowed part of the right plane: 29.8 cd/m²). The luminance values in the shadowed and lighted fields in the right plain remained approximately the same as the position of the spotlight changed (±4%).

6.2. Results and discussion

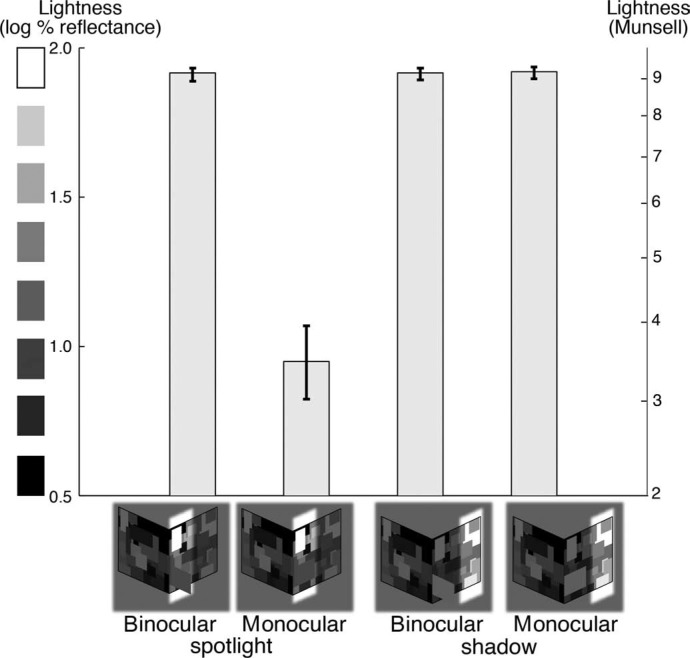
Figure 7 plots mean target lightness as its perceived position changed across the viewing conditions (monocular vs. binocular), for the spotlight and the shadow conditions.

Figure 7.

Experiment 4. Target lightness when both the perceived plane and perceived field of illumination of the target change from binocular to monocular viewing (the spotlight condition) and when only the perceived plane changes while the target's field of illumination remains the same (the shadow condition). The figure follows the same conventions of data presentation as in Figure 3.

A 2 × 2 ANOVA with viewing condition (monocular vs. binocular) and target's field of illumination (spotlight vs. shadow) as between-subjects factors revealed a viewing condition × field of illumination interaction, F(1, 56) = 211.36, p < 0.001. Target lightness decreased from nearly white (Munsell 9.2), when it appeared coplanar with the shadowed plane in the binocular viewing, to dark gray (Munsell 3.6), when it appeared coplanar with the multi-lit plane in monocular viewing, but only when the change of the perceived plane of the target was accompanied by a change in the target's perceived field of illumination, t(28) = 14.84, p < 0.001 (the main effects of viewing condition and the target's field of illumination: F(1, 56) = 207.84 and F(1, 56) = 211.36, respectively, both p < 0.001). In contrast, when the perceived target position changed from coplanar with the shadowed plane to coplanar with the shadowed region of the multi-lit plane, target lightness remained the same. Consequently, the depth effect was approximately zero in the shadow condition, but as large as 0.97 log% reflectance (5.6 Munsell steps) in the spotlight condition.

The results indicate that target lightness depends on the highest luminance in its field of illumination and not the highest coplanar luminance. When the highest luminance in target's field of illumination is the same across planes, as in the shadow condition, target lightness does not change despite the change in its perceived spatial position.

One possible interpretation of these results is that the depth effect on lightness is mediated by a change in perceived illumination (Howe, 2006). Our findings are indeed consistent with those of Howe, who performed a series of experiments to tease apart the relative contribution of coplanarity and perceived illumination in the effect of depth on lightness. He found that when the perceived illumination of a target is held constant, the change in perceived depth of the target “affects lightness only for some subjects” and concluded that the differences in perceived illumination “seem to influence a target lightness more than do coplanar relations” (Howe, 2006, pp. 298 and 299).

It is generally agreed that perceived lightness covaries with perceived illumination. This need not imply that lightness is derived from perceived illumination. But even if this were the case, the operations by which the illumination level is determined would need to be specified. Arend (1994) has pointed out that there are two separate components to this question: first, how the visual system identifies fields of illumination in the image and, second, how the illumination level is computed within each identified field?

The concept of planes in the coplanar ratio principle provides a partial answer to the first question, but sidesteps the second question by implying that lightness is computed directly and making only an indirect reference to illumination level through the luminance range constraint.

Anchoring theory, on the other hand, explicitly specifies units in the image within which target lightness is determined by identifying factors that segregate frameworks (mainly depth and shadow boundaries). And although it does not yet include a component for predicting perceived illumination, Gilchrist and colleagues (1999, p. 830) have suggested that the “perceived level of illumination is closely associated with the highest luminance in the framework.” This is based on empirical work showing that the perceived illumination level correlates with the highest luminance (Kozaki, 1973; Oyama, 1968; Zdravković, Economou, & Gilchrist, 2012). Note, however, that anchoring theory does not propose that the visual system needs to compute illumination level in order to get information about lightness, but rather that illumination is computed from image data in parallel with surface lightness.

7. General discussion

Figure 8 summarizes the changes we observed in the depth effect on lightness across our experimental manipulations. For each target and condition, we define a depth effect as the difference in the perceived lightness of the target as its perceived position changes from coplanar with the shadowed plane to coplanar with the lighted plane. We evaluated the reliability of the observed depth effects via the same bootstrap procedure as we used for mean target lightness (Efron & Tibshirani, 1993): for each experimental condition, we randomly sampled with replacement 20 matches from the set of actual target matches and computed the depth effect from the resampled data. We then computed the mean depth effect over 2,000 iterations of the resampling. Figure 8 shows the depth effect computed from actual matches (no different from the mean bootstrapped depth effect) with error bars representing bootstrapped 95% confidence intervals. The depth effect is shown in white for the lower target (all experiments) and in black for the upper target (Experiment 1).

Across most of our experimental conditions, we replicated the basic depth effect on lightness (Gilchrist, 1977, 1980): when the perceived position of the target changed from coplanar with the shadowed plane to coplanar with the lighted plane, the perceived target lightness decreased although the retinal surround of the target remained the same. The only exception was the shadow condition in Experiment 4, which showed that a change in the highest luminance in the target's field of illumination is necessary for the depth effect on lightness.

The majority of our findings are consistent with anchoring theory, which predicts that (1) due to co-determination, the target coplanar with the shadowed plane will always be perceived as slightly darker than white, while the target coplanar with the lighted plane will be perceived as slightly lighter than black; (2) the size of this depth effect varies as a function of display complexity: increasing articulation by increasing the number of elements in the plane lightens the target coplanar with the shadowed plane and increases the depth effect (Experiments 1 and 2; Figure 8); (3) the depth effect on lightness does not change when the luminance of coplanar surfaces adjacent to the target changes as long as the highest coplanar luminance remains the same, supporting the anchoring theory claim that lightness depends not on the adjacent but on the highest coplanar luminance (Experiment 3); finally, (4) when the planes in the display contain multiple fields of illumination, target lightness depends on the highest luminance in its field of illumination and not the highest luminance in its plane (Experiment 4): manipulating the spatial distribution of fields of illumination changes the effective grouping for lightness and limits the local lightness computation to the target's most immediate framework defined by a penumbra.

Perhaps it is not surprising that anchoring theory accounts better for our data than the coplanar ratio principle, because in some ways it evolved from it, and is more developed. But our findings have important implications for broader issues in lightness theory.

As far as anchoring theory is concerned, further refinement of the model is necessary, particularly concerning the mechanism by which articulation affects lightness. In its current formulation, anchoring theory assumes that an increase in articulation affects lightness directly, by increasing the strength of the local framework. Thus, anchoring theory fails to predict both (1) the absence of articulation effect on the lightness of the shadowed target (and the depth effect) in binocular viewing of Experiment 1 and (2) the increase in lightness of the shadowed target (and the depth effect) associated with increased articulation of either plane in the display, and not only the shadowed one (Experiment 2).

Both of these findings suggest that the effect of articulation on lightness may be closely related to the degree to which the frameworks in the image are segregated. When the display articulation is low, it is possible that there is some ambiguity about the spatial position of the targets in monocular viewing. This is because in monocular viewing the illusory grouping of each target with its depth plane relies solely on linear perspective. In binocular viewing, in addition to binocular disparity, other depth cues such as convergence, accommodation and motion parallax provide information about the target's position and strengthen its grouping with the plane from which it extends. Increasing articulation of either plane might decrease the ambiguity about spatial arrangement and strengthen both the segregation of the two depth planes and the grouping of each target with its orthogonal plane in monocular viewing. The more the target is grouped with a plane, the more its lightness depends on luminance relations within that plane (Koffka, 1935)—or, from the perspective of anchoring theory, the locally computed lightness values carry more weight in the computation.

This articulation-segregation hypothesis can account for the absence of effect of articulation on the lightness of the lower target (and its depth effect) in binocular viewing of Experiment 1 as well. In the case of already strong framework segregation in the binocular viewing, increasing or decreasing articulation would have a small effect. But when segregation is weaker, as in the monocular viewing, articulation may strengthen the segregation and facilitate grouping of elements into frameworks, just as we observed.

The hypothesis that articulation affects lightness indirectly, by strengthening framework segregation, in turn increasing local framework weights, would expand the current understanding of articulation within anchoring theory and would account well for our current findings, but requires further testing.

The experiments presented in this paper are part of a larger study aiming to revisit the question of when and how perceived lightness depends on perceived depth, and to systematically test how spatial and photometric factors known to influence lightness computation modulate the depth effect (see also Radonjić, Todorović, & Gilchrist, 2010). Our findings contribute to the growing literature showing that perceived spatial arrangement plays a significant role in color and lightness perception (Bloj, Kersten, & Hurlbert, 1999; Bloj et al., 2004; Boyaci, Doerschner, & Maloney, 2006; Boyaci, Maloney, & Hersh, 2003; Knill & Kersten, 1991; Logvinenko & Menshikova, 1994; Pessoa, Mingolla, & Arend, 1996; Ripamonti et al., 2004; Taya, Ehrenstein, & Cavonius, 1995) and provide a rich set of data that need to be accounted for by any comprehensive theory of lightness.

For example, our findings challenge low-level theories that emphasize the role of local contrast in lightness computation, as well as more complex spatial filtering models such as the ODOG model of Blakeslee and McCourt (2003, 2004) and its FLODOG variant (Robinson, Hammon, & de Sa, 2007), which in their current forms fail to account for effects of depth on lightness (brightness). Our findings also challenge decomposition models (Adelson & Pentland, 1996; Anderson & Winawer, 2005; Bergström, 1977; Gilchrist et al., 1983), which do not yet accommodate the pronounced effect of articulation.

Equivalent illuminant models (Bloj et al., 2004; Boyaci et al., 2003; Boyaci, Doerschner, & Maloney, 2004; for review see Brainard & Maloney, 2011) that emerged in the last decade offer an alternative approach for understanding lightness computation in three-dimensional scenes. Unlike anchoring theory, this class of models assumes that the visual system estimates the spectral and spatial characteristics of illumination in the scene (the equivalent illuminant) and then discounts the estimated illuminant from the image data to recover surface reflectance. The main challenge for such models is to specify how the visual system estimates the illuminant. Currently, two complementary approaches to this problem are in development. One focuses on identifying the cues to illumination in the scene to which the visual system is sensitive (Boyaci et al., 2006; Kraft, Maloney, & Brainard, 2002; Yang & Maloney, 2001). The other aims to develop Bayesian algorithms that can compute the equivalent illuminant from the image and compare the performance of such algorithms to observers' data (Allred & Brainard, 2013; Brainard et al., 2006). Our experiments are not designed to test the predictions of this class of models against anchoring theory. However, they provide valuable data that can be used to test the predictions of equivalent illuminant models as they develop to account for complex scenes.

Biography

Ana Radonjić studied psychology at the University of Belgrade, where she caught the science bug and got interested in vision. She received her PhD from Rutgers University studying surface lightness perception in complex three-dimensional configurations under the supervision of Dr. Alan Gilchrist. She is currently a postdoctoral researcher with Dr. David Brainard at University of Pennsylvania. She investigates mechanisms underlying color and lightness constancy using natural stimuli and natural tasks.

Alan L. Gilchrist received his BA in psychology at Portland State University and PhD at Rutgers University in 1975. After a postdoctoral fellowship at Bell Laboratories, he spent five years at Stony Brook University before returning to Rutgers in 1981. He conducts research on the perception of surface lightness and color. He is the founder of Club Vision, a consulting editor of Perception/i-Perception, the editor of Lightness, Brightness and Transparency (1994), and the author of Seeing Black and White (2006).