Are All Letters Really Processed Equally and in Parallel? Further Evidence of a Robust First Letter Advantage

Abstract

This present study examined accuracy and response latency of letter processing as a function of position within a horizontal array. In a series of 4 Experiments, target-strings were briefly (33 ms for Experiment 1 to 3, 83 ms for Experiment 4) displayed and both forward and backward masked. Participants then made a two alternative forced choice. The two alternative responses differed just in one element of the string, and position of mismatch was systematically manipulated. In Experiment 1, words of different lengths (from 3 to 6 letters) were presented in separate blocks. Across different lengths, there was a robust advantage in performance when the alternative response was different for the letter occurring at the first position, compared to when the difference occurred at any other position. Experiment 2 replicated this finding with the same materials used in Experiment 1, but with words of different lengths randomly intermixed within blocks. Experiment 3 provided evidence of the first position advantage with legal nonwords and strings of consonants, but did not provide any first position advantage for non-alphabetic symbols. The lack of a first position advantage for symbols was replicated in Experiment 4, where target-strings were displayed for a longer duration (83 ms). Taken together these results suggest that the first position advantage is a phenomenon that occurs specifically and selectively for letters, independent of lexical constraints. We argue that the results are consistent with models that assume a processing advantage for coding letters in the first position, and are inconsistent with the commonly held assumption in visual word recognition models that letters are equally processed in parallel independent of letter position.

1. Introduction

The computation of letter identity and localization within orthographic strings have been the focus of extensive experimental and modeling work (e.g., Adelman, 2011; Davis, 2010; Gomez, Ratcliff, & Perea, 2008; Whitney, 2001; for a review, see Grainger, 2008). Most models converge on the notion of parallel letter processing: information about the identity of all letters within a given word (or nonword) begins processing at the same time, independent of their location within the letter-array. This can be contrasted with more serial models (Whitney, 2001; see also Whitney & Cornelissen, 2008) in which there is a left-to-right processing scan, at least in left-to-right alphabetical languages.

Adelman, Marquis and Sabatos-DeVito (2010) recently provided some intriguing evidence in favor of parallel letter-processing. In their experiment, four-letter words were briefly presented between both a forward and backward mask of hash marks (######). Participants were then presented with 2 alternatives, one corresponding to the target word and the other representing a distracter word for a forced choice recognition test. Critically, the target and the distracter differed by only one letter and the position of the mismatch between targets and distracters was manipulated across all four letter positions (e.g., sung and lung for a mismatch in the first position, fish and fist for a mismatch in fourth position). The duration of the target words’ display was varied between participants, ranging from 12 to 54 ms in 6 ms increments, thus allowing one to track performance across stimulus duration. The rationale underlying this paradigm is straightforward: Serial accounts of letter processing claim that each letter takes 10 to 25 ms to be processed. If the serial account is correct, then performance should increase along a left to right trajectory as a function of the duration of the target display. In contrast, if a more parallel account is correct, there should be more of a step function, wherein all letters go above chance at a given duration. The results indicated that when the prime was displayed for 18 ms performance was at chance at all positions, whereas with a small increase of only 6 ms performance was significantly above chance for all letter positions. These data are most consistent with parallel processing in which information about all the letters in target-words become available after a given amount of time, irrespective of their location within the left-to-right horizontal sequence.

Although accuracy was significantly above chance in all positions at the 24 ms prime duration, a left-to-right decrement in accuracy was also observed in the Adelman et al. study. In other words, accuracy was higher when the mismatch was in first-position, and linearly decreased across the other positions, reaching its lowest level in fourth-position. Adelman et al. ascribed the horizontal decrease in accuracy to differences in the efficiency of information extraction as a function of letter-position, even though all letters are processed in parallel.

Differences in the detection of letters as a function of position within target strings have been investigated in several experimental paradigms. The most common paradigm involves participants simply reporting the identity of the probed letter instead of engaging in the forced choice of two words as in the Adelman et al. paradigm. The results from these letter detection studies typically indicate that performance is optimal at fixation and at end-letters (e.g., Merikle, Coltheart, & Lowe, 1971; Merikle, Lowe & Coltheart, 1971; Mewhort & Campbell, 1978; Stevens & Grainger, 2003). Most notably, such a pattern holds only for stimuli made of letters (or digits). When target stimuli are made of non alphanumeric characters (i.e., symbols such as %, /, −), the advantage for end-positions disappears, leaving higher accuracy only for the character at fixation (Mason, 1982; see also Hammond & Green, 1982; Mason & Katz, 1976).

This latter finding has been recently replicated and extended in a series of studies by Tydgat and Grainger (2009; see also Chanceaux & Grainger, 2012; Grainger, Tydgat, & Isselé, 2010). In these studies 5 character arrays were presented for 100 ms and both forward and backward masked. Across a variety of manipulations, Tydgat and Grainger found a consistent advantage in identifying letters and digits, but not symbols, occurring in the leftmost position of the array (first position advantage). In addition, they found that there was an advantage for the character occurring at fixation irrespective of the type of character (i.e., alphanumeric or non alphanumeric characters). According to Tydgat and Grainger (2009) the first position advantage detected selectively for letters and digits but not for symbols suggests a mechanism optimized to process first position of letter/digit strings. Indeed there are a number of important constraints provided by the first letters. For example, letters occurring in first position are more constraining for lexical identity compared to letters occurring in other positions (Clark & O’ Regan, 1999; Grainger & Jacobs, 1993). In addition, letters in the initial position would be particularly important for mapping orthography to phonology, at least in models that posit a grapheme parser operating left-to-right (Perry, Ziegler, & Zorzi, 2007). Because of the functional utility of the first letter position, Tydgat and Grainger (2009) hypothesized that receptive fields are elongated to the left, in the direction of the leftmost position. Given the absence of any interfering character to the left of letters in first position (in left to right alphabetic reading languages), this left elongated shape of the detectors optimizes processing of the letters occurring in the initial position, readily explaining the consistent first position advantage detected across the different experiments (for further evidence and arguments, see also Chanceaux & Grainger, 2012; Grainger, Tydgat, & Isselé, 2010).

The primary aim of the present research is to investigate how accuracy in letter identification varies as a function of the location within the experimental paradigm used by Adelman and colleagues (2010). As noted, this paradigm involves a forced choice decision between two alternative words. This is somewhat different than the Tydgat and Grainger paradigm in which single letter, as opposed to word level, processing is emphasized. As such, the Adelman et al. paradigm may offer greater insight into how letters are differentially recognized in visual word recognition, i.e. where stimuli are real words and attention is directed to whole-word representations. Interestingly, Adelman et al. did not find evidence of a performance advantage of the letters presented at fixation, as obtained by the Tydgat and Grainger study, suggesting that the two paradigms are tapping different processes. Moreover, if the Tydgat and Grainger finding of an initial position advantage in letter processing extends to whole word processing then one should observe a similar pattern in the Adelman et al. whole word paradigm.

Although in Adelman et al’s (2010) data accuracy was numerically higher in the first position (for similar results, see also Gomez et al., 2008), emphasis was placed on parallel processing across letters. Because of the importance regarding the special status of the first position within other paradigms (e.g., Merikle, Coltheart, & Lowe, 1971; Merikle, Lowe, & Coltheart, 1971; Mewhort & Campbell, 1978; Tydgat & Grainger, 2009), we first attempt to replicate Adelman et al.’s pattern to further examine if one can provide evidence of an initial letter advantage in this paradigm. Given the constraints provided by the first letter to lexical identity, and given the hypothesis that letter-detectors are specifically adapted to capitalize on such a constraint by optimizing processing of initial letter (as hypothesized by Tydgat & Grainger, 2009), a first position advantage should be reliably detected. These data would suggest that there is a special status for word initial letter representations in lexical processing. Moreover, it is possible that there is a letter level serial processing mechanism in this paradigm, and if this were to be found then one might expect a more linear decrease in performance from left to right positions. As noted there was some tendency in the Adelman et al. data which was consistent with this possibility.

In our first study we examined words that ranged from 3 to 6 letters. We were particularly interested in whether the Adelman et al. results with only four letter words could be extended to other lengths. It is possible that one may find evidence for more parallel processing with shorter words and more serial processing with longer words. In the first experiment, length was blocked, so that individuals might tune the visual system to a particular visual angle. This is most consistent with the Adelman et al. and the Tydgat and Grainger studies in which only a single length was used. Finally, we measured both response latencies and accuracy in the present study, which extends previous studies that have most commonly focused on accuracy measures.

2. Experiment 1

2.1 Method

2.1.1 Participants

Thirty-two undergraduate students from Washington University in St. Louis participated in the experiment for course credit or compensation ($10). All were native English speakers and reported normal or corrected-to-normal vision.

2.1.2 Materials

Stimuli consisted of 3, 4, 5, and 6 letter words. For each letter-position within each length, 20 pairs of words were selected. Within each pair of words, the two words differed by only one letter at a given position (see Table 1, for examples of the pairs selected). This resulted in the selection of 360 pairs of words (20 pairs per position at each length). Due to an error in initial coding of the stimuli, the final materials resulted in 21 pairs for the third position in four- and five-letter words, 21 pairs for the fourth position in 5-letter strings, 19 pairs for the first position of four-letter string, 19 for the second position of five-letter string and 19 for fifth position of 6-letter string. For all other positions within different lengths there were 20 pairs of words.

Table 1.

Examples of stimuli used in Experiment 1 and 2.

Position	Three-letter words	Four-letter words	Five-letter words	Six-letter words
1	hug - rug	zero - hero	cheat - wheat	wizard - lizard
2	toe - tie	ruin - rain	along - among	poison - prison
3	bug - bus	deny defy	coach - couch	riding - rising
4	-	fist - fish	floor - flour	strong - string
5	-	-	chair - chain	breach - breath
6	-	-	-	threat - thread

The two alternatives of the pairs were split into two different lists, for balancing and counterbalancing purposes, with one item serving as the target and the other item serving as the distracter for a given participant. For each length, within each position the lists were not statistically different in terms of word-frequency (raw and log-transformed) or number of orthographic and phonological neighbors (all ps > .27). Moreover, within each length, the selected words were comparable across different positions in terms of word-frequency (raw and log-transformed), orthographic and phonological neighborhood (all Fs < 1.76, all ps > .13). Properties of the experimental items are listed in Table 2, and the items are available upon request.

Table 2.

Properties of experimental items used in Experiments 1 and 2.

Word Length	Log Freq		Orth N		Phon N
	List 1	List 2	List 1	List 2	List 1	List 2
Three letters
1	8.4	8.41	14.2	14.3	24.25	27.5
2	8.43	8.66	13.7	14.55	28.5	26.3
3	8.56	8.59	14.9	13.65	26.95	28.6
Four letters
1	8.47	8.77	5.63	5.89	14.68	16.74
2	8.75	8.51	5.65	5	13.65	16.25
3	8.62	8.39	5.52	5.76	13.14	13
4	8.47	8.53	5.6	5.8	17.55	21.5
Five letters
1	8.56	8.76	3.2	3	10.95	11.15
2	8.33	8.44	3	3.26	8.79	8.58
3	8.7	8.79	3.1	2.86	6.76	8.57
4	8.39	8.03	2.7	3.25	6.5	6.8
5	8.58	8.32	3.25	3.2	9.25	8.6
Six letters
1	8.67	8.49	2.6	2.7	8.15	7.25
2	8.71	8.82	3.3	3.05	7.6	6.65
3	8.45	8.48	2.95	3.15	4.8	5.1
4	8.48	8.26	3.24	3.29	4.29	5.52
5	8.55	8.3	2.63	2.53	5.47	6.32
6	8.79	8.83	2.5	2.6	4.2	5.55

Note. Log Freq = log-transformed frequency. Orth N = orthographic neighborhood density. Phon N = phonological neighborhood density. All variables have been retrieved form the English Lexicon Project Database (Balota et al., 2007), where frequency values are taken from the Hyperspace Analogue to Language (HAL) frequency norms (Lund & Burgess, 1996).

As noted earlier, length was blocked, such that all items of a given length were presented within the same block. The order of presentation of the different blocks was counterbalanced via a Latin square design. Filler pairs were selected in order to have the same number of trials across the different blocks. For example, for six-letters words, 120 experimental pairs were selected (20 for each one of the six letter positions), but just 60 pairs were selected for three-letter words (again, 20 pairs for each one of the three letter-position). Hence, 60 filler pairs were selected for three-letter-words (20 for each position), 40 for four-letter words (10 for each position) and 20 for five-letter words (4 for each position), so that 120 target-words were displayed for each length within a block. Filler pairs were constructed as experimental pairs; however, these items were not included in the analyses.

Lists (i.e., which item of a pair occurred as the target and which served as the distracter) were counterbalanced across participants. The location of targets and distracters in the two-alternative forced choice visual display (see Apparatus and Procedure) was counterbalanced as well, so that each word (both as a target and as a distracter) would appear equally often as a response alternative in the right and in the left visual field.

2.1.3 Apparatus and Procedure

Participants were tested in a dimly lit testing-room, with a maximum of 6 participants running at the same time. Each testing station was isolated from the flanking stations with divider screens that minimized any cross-station interaction. Each participant was seated at a distance of approximately 40 cm from the computer monitor in individual testing stations. Data were collected on Pentium 4 computers using E-Prime 1.1 (Schneider, Eschman, & Zuccolotto, 2001).

Each trial started with a forward mask consisting of a string of 6 hash marks (######) displayed at the centre of the screen. After 895 ms, the forward mask was replaced by the lower case target word, which stayed on the screen for 33 ms and was followed by a blank screen of 17 ms. These display parameters were based on pilot data indicating that all participants were above chance. After the blank screen, the backward mask (the same as the forward mask) was presented along with the two lower case response alternatives, presented below the backward mask, one in the left and one in the right visual field (the experimental procedure is schematically represented in Figure 1). The display remained on the screen until participant’s response (key press). If no response was detected, the display was terminated after 5000 ms. Trials were separated by an inter-trial interval of 1600 ms.

Figure 1.

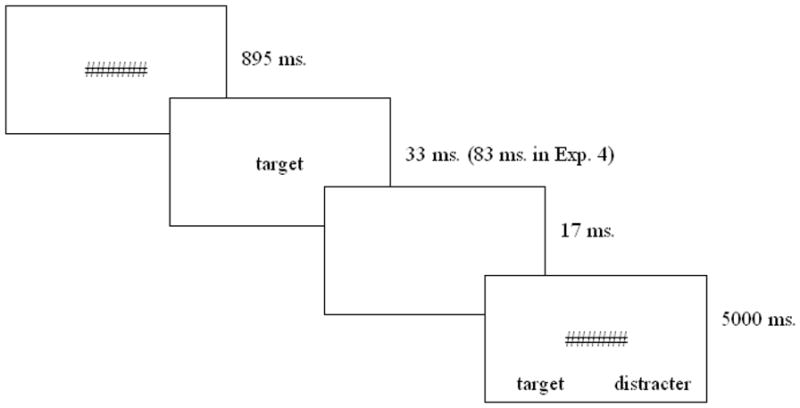
Representation of the experimental procedure. Forward and backward masks (a string of six hash-marks) were the same across all the different conditions (length/stimulus type) of all the experiments reported. Stimuli and masks were displayed in Courier New 18 font.

Each block was preceded by 4 practice trials of the same length for that block. At the end of each block, participants were prompted to take a break, during which feedback on accuracy of responses (in terms of percentage of correct responses) was given. The experimental session lasted about 45 minutes.

Participants were instructed to fixate at the middle of the string of hash marks appearing at the beginning of each trial. They were told that a word would be briefly displayed between the hash marks, and that their task was to select, among the two subsequently presented response alternatives, which target was previously presented by pressing the A key when the correct alternative is placed at the left of fixation and the L key when it is placed at the right of fixation. In case they were not sure, they were instructed to guess by selecting the alternative that, in their opinion, had the best match with the previously presented target. Although accuracy was emphasized, they were also encouraged to make their response as quickly as possible.

2.2 Results

Response latencies and accuracies were analyzed across participants and items, yielding respectively F₁ and F₂ statistics. Position was considered as a within-subject factor in the analysis by-participant, and as a between-item factor in the item analysis. Because the number of positions varied as a function of length, separate ANOVAs were conducted within each length, in order to assess variations in accuracy and response times (RTs) as a function of the position in the string.

Trials in which an error in the timing of the visual displays was detected (0.24%) were removed from the analyses.¹ For analyses of response latencies, errors (18.83%) were not considered. RTs below 200 ms (0.03%) and RTs 2.5 SD from each participant’s mean (3.03%) were excluded from the analyses.²

2.2.1 Accuracy

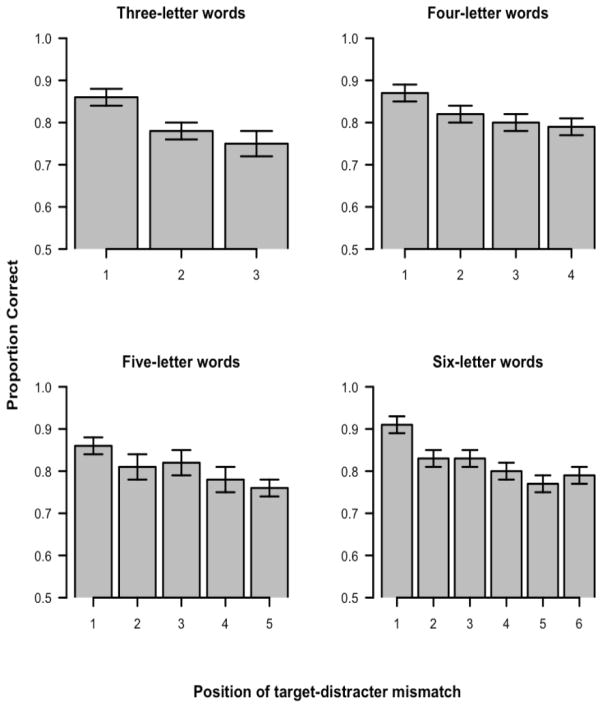
Accuracies as a function of word-length and position of the mismatch between distracter and target are displayed in Figure 2.

Figure 2.

Experiment 1: Mean proportion of correct responses as a function of position of the target-distracter mismatch and word-length. Error bars represent standard error of the mean.

The effect of position was significant for three-letter words (F₁ [2, 62] = 14.61, MSE = .007, p < .001; F₂ [2, 117] = 7.43, MSE = .016, p < .01), four-letter words (F₁ [3, 93] = 7.59, MSE = .006, p < .001; F₂ [3, 156] = 4.26, MSE = .014, p < .01), five-letter words (F₁ [3.09, 95.66] = 6.05, MSE = .01, p < .01; F₂ [4, 195] = 4.03, MSE = .015, p < .01) and six-letter words (F₁ [5, 155] = 10.56, MSE = .007, p < .001; F₂ [5, 234] = 6.09, MSE = .015, p < .001). Note that, for five-letter words, the effect of position violated sphericity and hence the Grennhouse-Geisser correction was applied. Planned comparisons between positions within each length are reported in Table 3. The results produced a consistent first position advantage: when the mismatch between target and distracter occurred at the first position, accuracy was consistently higher compared to when the mismatch occurred in other positions.

Table 3.

Planned comparisons for proportions of correct responses (ACC) and reaction times (RT) between different positions of target-distracter mismatch within each word-length in Experiment 1.

Word length and positions of mismatch	ACC		RT
	t1	t2	t1	t2
Three-letter words
1 vs. 2	4.19***	2.99**	−2.45*	−2.59*
1 vs. 3	5.71***	3.93**	−3.25**	−2.13*
2 vs. 3	1.09	.81	.26	.47
Four-letter words
1 vs. 2	5.56**	2.27*	−6.19***	−5.12***
1 vs. 3	3.36**	3.00**	−5.83***	−3.89***
1 vs. 4	4.69***	3.12**	−5.16***	−4.01***
2 vs. 3	1.03	.88	1.39	.98
2 vs. 4	1.63	1.18	1.42	.86
3 vs. 4	.44	.36	.49	−.11
Five-letter words
1 vs. 2	1.79°^	1.79°^	−5.73***	−5.32***
1 vs. 3	2.08*^	1.66	−5.69***	−5.44***
1 vs. 4	3.42**	3.54**	−6.17***	−6.7***
1 vs. 5	5.92***	3.28**	−5.48***	−4.30***
2 vs. 3	−.24	−.18	−.74	.31
2 vs. 4	1.38	1.36^	−1.85°^	−1.57^
2 vs. 5	1.99°	1.68°^	.24	.56
3 vs. 4	2.00°	1.61^	−.98	−1.99°^
3 vs. 5	3.1**	1.9°^	.95	.31
4 vs. 5	1.27^	.76	2.02 °	1.99°
Six-letter words
1 vs. 2	3.94***	3.38**	−5.72***	−5.58***
1 vs. 3	4.5***	3.40**	−6.32***	−5.81***
1 vs. 4	4.76***	4.15***	−8.03***	−5.67***
1 vs. 5	6.49***	5.17***	−6.79***	−6.2***
1 vs. 6	5.34***	4.71***	−6.13***	−5.35***
2 vs. 3	.41	.30	−.10	.02
2 vs. 4	1.35	1.13	−.99	−.27
2 vs. 5	3.63**	2.29*	−1.97°^	−.96
2 vs. 6	2.15*	1.65^	−1.31	−1.07
3 vs. 4	1.02	.79	−.89	−.29
3 vs. 5	2.42*	1.91°^	−1.45	−1.01
3 vs. 6	1.73	1.28	−1.19	−1.11
4 vs. 5	1.82°	1.15	−.68	−.68
4 vs. 6	.66	.49	−.35	−.86
5 vs. 6	−1.00	−.68	.26	−.27

Note. t₁ refers to paired-sample t-test conducted within participants. t₂ refers to independent-sample t-test conducted between items.

^***p < .001;

^**p < .01;

^*p < .05;

^°p < .1. Results, in terms of significance, were the same across analyses on raw accuracies/response latencies and arcsine-root-transformed accuracies/z-score-transformed response latencies, except where marked (^{^}).

2.2.2 Response latencies

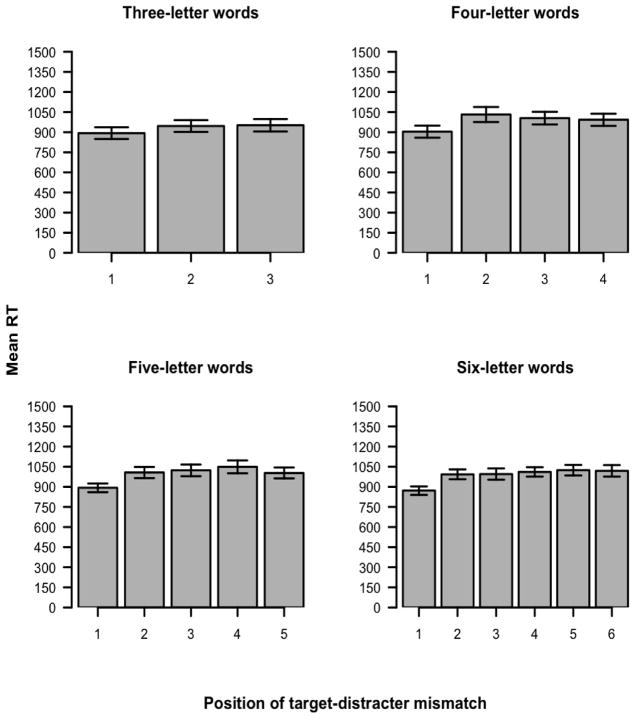
Response latencies as a function of word length and position of target-distracter mismatch are displayed in Figure 3.

Figure 3.

Experiment 1: Mean reaction times (RT) as a function of position of the target-distracter mismatch and word-length. Error bars represent standard error of the mean.

The effect of position was significant for three- (F₁ [2, 62] = 5.07, MSE = 6665.24, p < .01; F₂ [2, 117] = 3.64, MSE = 13469.2, p < .05), four- (F₁ [2.28, 70.8] = 13.49, MSE = 9601.88, p < .001; F₂ [3, 156] = 8.9, MSE = 12576.79, p < .001), five- (F₁ [4, 124] = 14.83, MSE = 7759.61, p < .001; F₂ [4, 195] = 12.78, MSE = 13439.2, p < .001), and six-letter words (F₁ [5, 155] = 16.93, MSE = 6166.53, p < .001; F₂ [5, 234] = 10.0, MSE = 12700.67, p < .001). Planned comparisons between positions within each length are presented in Table 3. Consistent with the accuracy data, there is a clear advantage of the first position in the response latency data.

2.3 Discussion

The results converged with the results reported by Adelman et al. (2010) in showing that accuracy is higher in the first position and appears to slightly decrease across the remaining positions. Moreover, there were clear effects in response latencies for the first positions. (Adelman et al. did not report response latencies.) This effect is quite consistent across different lengths, and so the effect is not dependent upon visual acuity at least within the lengths examined. Interestingly, there is no evidence of an advantage for the mismatch at fixation as observed in the Tydgat and Grainger (2009) study.

In the second experiment, we examined the possibility that the effect observed in the first experiment is due to visual attention being tuned to a given length of a word. As noted in previous studies, participants typically only receive a single length, and this was the case in the Adelman et al. study. It is possible that subjects may focus attention at the beginning part of the stimulus. Of course, this would limit the generalizability of these results since words typically vary in length in standard word recognition studies, and more importantly across different fixations during reading. Hence, in Experiment 2, we randomly intermixed length to examine if the initial position effect persists.

3. Experiment 2

3.1 Method

3.1.1 Participants

Thirty-two undergraduate students from Washington University in St. Louis participated to the experiment for course credit or compensation ($10). All were native English speakers and reported normal or corrected-to-normal vision. Two participants were replaced because their overall accuracy in the experiment was near chance: their overall mean accuracy was .53 and .56 respectively, while for other participants accuracy ranged from .63 to .93, with a mean overall accuracy of .83 (SD = .07). The pattern of reliable effects did not change when these participants were included in the analyses.

3.1.2 Materials

The same set of words used in Experiment 1 (both experimental and filler items) was used in this second experiment.

3.1.3 Apparatus and procedure

Apparatus and procedure were as in Experiment 1. The only difference was that words of different lengths were presented randomly intermixed. There was a single practice session at the beginning of the experiment, with all the practice items used in Experiment 1 randomly intermixed. The experiment consisted of 4 experimental blocks, with 120 trials per block.

3.2 Results

As in Experiment 1, filler trials and trials in which an error in the timing of the visual displays was detected (0.18%) were removed from both the analyses. For analyses of RTs, only correct responses were considered. In addition, RTs below 200 ms (0.02 %) and RTs 2.5 SD from each participant’s mean (2.89 %) were excluded.

3.2.1 Accuracy

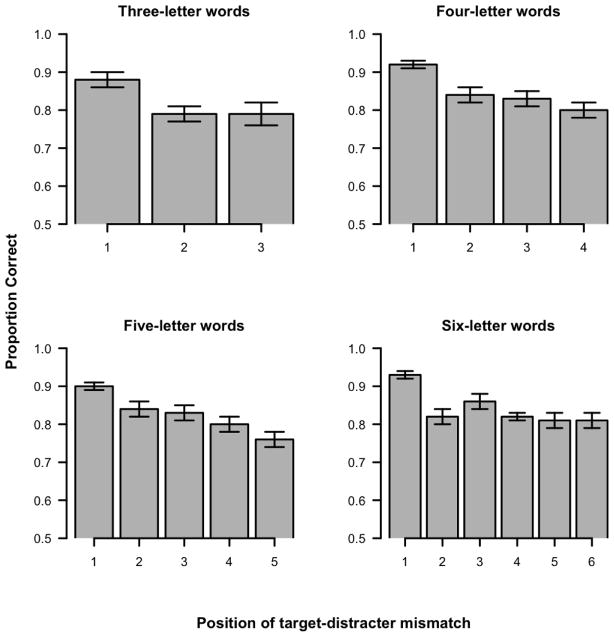
Accuracy as a function of word-length and position of the target-distracter mismatch are displayed in Figure 4.

Figure 4.

Experiment 2: Mean proportion of correct responses as a function of position of the target-distracter mismatch and word-length. Error bars represent standard error of the mean.

There was again a significant effect of position for three-letter words (F₁ [2, 62] = 11.13, MSE = .007, p < .001; F₂ [2, 117] = 5.27, MSE = .018, p < .01), four-letter words (F₁ [3, 93] = 11.64, MSE = .007, p < .001; F₂ [3, 156] = 7.51, MSE = .013, p < .001), five-letter words (F₁ [4, 124] = 9.34, MSE = .008, p < .001; F₂ [4, 195] = 7.77, MSE = .012, p < .001) and six-letter words (F₁ [5, 155] = 10.77, MSE = .007, p < .001; F₂ [5, 234] = 6.43, MSE = .014, p < .001). Planned comparisons between positions within each length are reported in Table 4. The results again show a consistent first position advantage. Specifically, when the mismatch between target and distracter occurs in the first position, accuracy is higher compared to when the mismatch occurs in other positions.

Table 4.

Planned comparisons for proportions of correct responses (ACC) and reaction times (RT) between different positions of target-distracter mismatch within each word-length in Experiment 2.

Word length and positions of mismatch	ACC		RT
	t1	t2	t1	t2
Three-letter words
1 vs. 2	4.39***	2.97**	−5.64***	−5.26***
1 vs. 3	4.51***	2.84**	−5.96***	−4.37***
2 vs. 3	.22	.15	.91	.59
Four-letter words
1 vs. 2	4.98***	2.92*	−8.23***	−5.51***
1 vs. 3	3.94***	4.17***	−6.57***	−5.49***
1 vs. 4	4.94***	5.50***	−5.35***	−4.63***
2 vs. 3	.57	.37	−.11	.11
2 vs. 4	2.20*	1.52^	.72	.51
3 vs. 4	1.40	1.36	.64	.41
Five-letter words
1 vs. 2	3.31**	2.79**	−8.21***	−5.90***
1 vs. 3	3.70**	3.92***	−7.14***	−7.17***
1 vs. 4	4.34***	4.20***	−9.83***	−6.89***
1 vs. 5	6.90***	4.79***	−6.38***	−6.30***
2 vs. 3	.32	.50	−.06	−.26
2 vs. 4	1.36	1.36	−2.16*	−1.72°^
2 vs. 5	2.82**	2.41*	−.25	−.36
3 vs. 4	1.03	1.08	−2.14*	−1.68°
3 vs. 5	2.77**	2.25*	−.20	−.15
4 vs. 5	1.86°^	1.24	1.85°	1.41
Six-letter words
1 vs. 2	6.04***	4.64***	−8.27***	−7.02***
1 vs. 3	3.61**	3.12**	−10.29***	−7.28***
1 vs. 4	7.78***	4.53***	−7.93***	−7.73***
1 vs. 5	6.57***	5.05***	−8.30***	−7.85***
1 vs. 6	6.61***	5.58***	−6.26***	−6.32***
2 vs. 3	−1.41^	−1.36	.53	.03
2 vs. 4	.03	.01	−.09	−.22
2 vs. 5	.62	.43	−1.01	−.99
2 vs. 6	.36	.31	.76	.47
3 vs. 4	1.90°	1.34	−.71	−.26
3 vs. 5	2.29*	1.77°	−1.57	−1.06
3 vs. 6	1.77°	1.79°	.33	.46
4 vs. 5	.75	.42	−1.00	−.84
4 vs. 6	.40	.29	1.25^	.72
5 vs. 6	−.25	−.17	1.87°	1.42

Note. t₁ refers to paired-sample t-test conducted within participants. t₂ refers to independent-sample t-test conducted between items.

^***p < .001;

^**p < .01;

^*p < .05;

^°p < .1. Results, in terms of significance, were the same across analyses on raw accuracies/response latencies and arcsine-root-transformed accuracies/z-score-transformed response latencies, except where marked (^{^}).

3.2.2 Response latencies

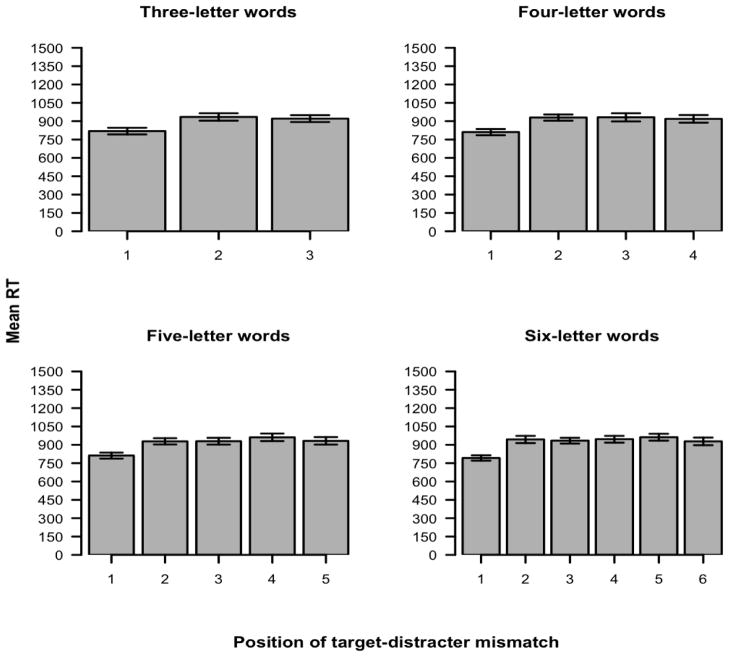
Response latencies as a function of word length and position of target-distracter mismatch are plotted in Figure 5.

Figure 5.

Experiment 2: Mean reaction times (RT) as a function of position of the target-distracter mismatch and word-length. Error bars represent standard error of the mean.

The effect of position was significant for three-, (F₁ [2, 62] = 24.27, MSE = 5253.95, p < .001; F₂ [2, 117] = 15.04, MSE = 11655.52, p < .001), four- (F₁ [3, 93] = 21.17, MSE = 5118.1, p < .001; F₂ [3, 156] = 12.06, MSE = 10767.22, p < .001), five- (F₁ [4, 124] = 27.37, MSE = 3940.07, p < .001; F₂ [4, 195] = 17.52, MSE = 8851.5, p < .001), and six-letter words (F₁ [5, 155] = 23.47, MSE = 5339.71, p < .001; F₂ [5, 234] = 17.32, MSE = 8773.27, p < .001). Planned comparisons between positions within each length are presented in Table 4. Again, when the mismatching letter for the distracter is in the first position, response latency was considerably faster.

3.2.3 Cross-experiment analysis

In order to examine whether blocked vs. intermixed presentation for items of different lengths produced any significant difference in the pattern of results, we conducted separate cross-experiment analyses for each word-length by including Experiment (1 vs. 2) as a factor in the ANOVAs. The results indicated that the position by experiment interaction was never significant in terms of accuracy or response latency. Interestingly, response latencies were faster in Experiment 2. Indeed, analyses by items showed main effects of Experiment both in accuracy and RTs for three- (accuracy: F₂ [1, 117] = 3.47, MSE = .008, p = . 06; RTs: F₂ [1, 117] = 7.45, MSE = 8711.94, p < .001), four- (accuracy: F₂ [1, 156] = 7.5, MSE = .008, p < .01; RTs: F₂ [1, 156] = 57.94, MSE = 8124, p < . 001), five- (accuracy: F₂ [1, 195] = 6.49, MSE = .008, p < .05; RTs: F₂ [1, 195] = 97.07, MSE = 6926.17, p < .001), and six-letter stimuli (accuracy: F₂ [1, 234] = 6.28, MSE = .008, p < .05; RTs: F₂ [1, 234] = 86.15, MSE = 6683.79, p < .001), with faster and more accurate responses in Experiment 2. These results were not fully paralleled in the analyses by participants, where only RTs for five-letter words displayed a similar trend (F₁ [1.62] = 3.07, MSE = 176238.81, p = .085), while for all other lengths, both in terms of accuracy and RTs, the effect of Experiment never reached significance (accuracy: all F₁s < 1.45, all ps > .2; RTs: all F₁s < 2.52, all ps > .12).

3.3 Discussion

Experiment 2 provides a clear replication and extension of the robust first-position advantage (both in accuracy and RTs) observed in Experiment 1. This experiment rules out the possibility that the first-position advantage is produced by participants focusing attention on a specific portion of the visual space. Because in Experiment 2 words of different lengths were presented randomly throughout the task, the letters in first position were unpredictably displayed at different spatial positions (i.e., at different eccentricities from fixation) across trials. Despite this fact, the first-position advantage was still robust for three-, four-, five-, and six-letter words in both accuracy and response latencies. Moreover, there was no evidence of an advantage for letters presented at fixation. Hence, the forced choice recognition paradigm of Adelman et al. produces some differences compared to letter recognition in the Tydgat and Grainger paradigm.

The final two experiments attempt to further explore the locus of the first position effect. For example, it is possible that the first position advantage is specifically tied to the lexical status of the targets, although evidence from other studies seems to question this claim. A recent study by Gomez et al. (2008) is informative here. In a paradigm similar to the present study, Gomez et al. produced a first position advantage for legal nonwords. However, given the difference in the duration of the stimuli across the two studies (60 ms in Gomez et al., 33 ms in the present experiments) and other subtle differences in the experimental paradigm (stimuli were not preceded by a forward mask in Gomez et al. experiments) it is important to further explore the issue in the present paradigm and also measure response latencies, which Gomez et al. did not report.

In addition to examining legal nonwords as in Gomez et al., we also examined randomly ordered consonant strings, and strings of symbols (e.g., @</&£). Given the stability of the pattern observed with words in the previous two experiments, and the possibility that words might bias an initial position effect, we excluded words from this experiment. If the first position-advantage is specifically tied to the lexical nature of the materials, the effect should be absent with this set of stimuli, albeit one might expect some effect for legal nonwords, which closely resemble real words. On the other hand, if the first-position advantage is a reflection of a mechanism specifically related to letter-processing (e.g., Chanceaux & Grainger, 2012; Grainger, Tydgat, & Isselé, 2010; Tydgat & Grainger, 2009), one would predict that the effect should still be found for legal nonwords and for random consonant strings, but not for symbols. Finally, if the effect is found even for symbols, this would represent strong evidence in support of the hypothesis that the first position advantage is a byproduct of specific operations prompted by the task itself, rather than by the stimuli.

4. Experiment 3

4.1 Method

4.1.1 Participants

Sixteen undergraduate students participated to the experiment for course credit or compensation ($10). All participants were native English speakers and reported normal or corrected-to-normal vision.

4.1.2 Materials

Legal nonwords were created by changing one letter from 5-letter words used in previous experiments. Hence, for each pair of words used in the previous experiments, the same change occurred in the two component words (e.g., if the pair was demon-lemon in the previous experiments, the nonword-pair would be domon-lomon). The position in which the letter was changed to form a nonword was equally distributed across the positions. Specifically, of the 20 word pairs in which the critical mismatch occurred in the first-position, nonword pairs were created by changing 5 pairs in each of the non-critical positions (i.e., second, third, fourth and fifth position). The same was true for the 20 pairs of words in which the critical mismatch occurred in the fourth and fifth position. For the 19 pairs in which the critical-mismatch occurred in the second position, nonword pairs were created by changing 4 word pairs in the first position, and by changing five word-pairs in the other non-critical positions (i.e., third, fourth and fifth position). Finally, for the 21 word-pairs in which the critical mismatch occurred in the third position, nonwords were created by changing 6 pairs of words in first position, and 5 pairs in all the other non-critical positions (i.e., second, fourth and fifth position). Care was taken in order to produce orthographically legal and pronounceable nonwords. Again, the members of the pairs were split into different lists, and, within each position, the two lists were not different in terms of number of orthographic neighbors, summed and mean bigram frequency (all ps > .14; see Table 5). Items across different positions of the target-distracter mismatch were also not statistically different on those same variables (all Fs < 1).

Table 5.

Properties of the nonwords used in Experiment 3.

	Orth. N		Summed Bigr.		Mean Bigr.
Position of mismatch	List 1	List 2	List 1	List 2	List 1	List 2
1	2.85	2.45	13266	13626	3316	3407
2	2.85	2.35	13165	11911	3291	2978
3	3.1	3.35	14447	14463	3612	3616
4	3.35	2.85	13612	11071	3403	2768
5	3.3	3.20	13391	13617	3348	3404

Note. Orth N = orthographic neighborhood density. Summed Bigr = summed bigram frequencies. Mean Bigr. = mean bigram frequencies. All variables have been retrieved from the English Lexicon Project Database (Balota et al., 2007).

Strings of consonants and symbols were created following Tydgat and Grainger (2009). Five-item arrays of consonants and five-item arrays of symbols were created by arranging quasi-random sequences of consonants (selected among a set of 9 consonants consisting of b,d,f,g,k,n,l,s, and t) or symbols (selected among a set of 9 symbols consisting of %, /, ?, @, }, <, £, §, and μ). The same letter or symbol was never repeated within each string. Each of the elements of the two sets was presented two times at each critical position (the position of the target-distracter mismatch) and 40 times at a non-critical position (i.e., not at the position of the target-distracter mismatch). This resulted in the creation of 18 pairs of consonant-strings and 18 pairs of symbol-strings for each of the five positions.

For all classes of stimuli, the presentation of each string as target or as distracter was counterbalanced across participants. The location of targets and distracter in the two-alternative forced choice visual display was counterbalanced as well, so that each string (both as a target and as a distracter) would appear equally often as a response alternative in the right and in the left visual field. Ten further pairs of target-distracter combinations were selected for each class of stimuli to be displayed in practice-trials. Different types of stimuli (i.e., nonwords, strings of consonants, and strings of symbols) appeared randomly intermixed throughout the experiment.

4.1.3 Apparatus and Procedure

Apparatus and experimental procedure were the same as in previous experiments. Stimuli of the three different classes were presented randomly intermixed throughout the task. After every 70 trials (total of 280 trials) participant were prompted to take a break, during which they were give feedback about their accuracy in terms of percentage of correct response. The experimental session lasted about 35 minutes.

4.2 Results

Trials in which an error in timing of the visual displays occurred (0.07%) were removed from all the subsequent analyses. For the analyses of RTs, errors (37.59%) were not considered. For trials with a correct response, latencies below 200 ms (0.21%) and 2.5 SD from the mean (2.69%) of each participant were removed.

4.2.1 Accuracy

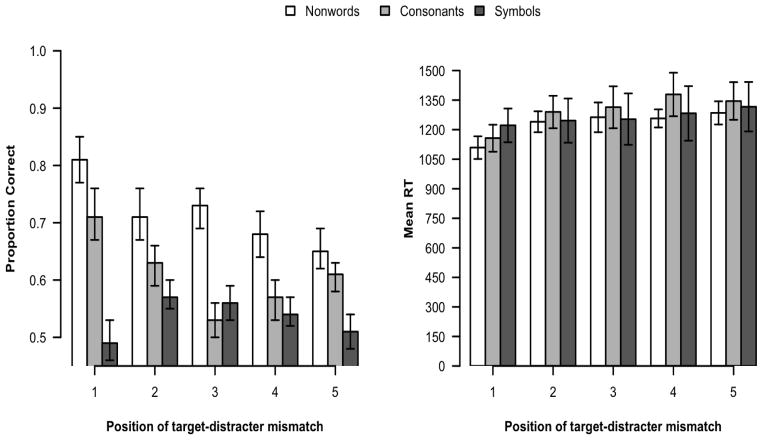
Mean proportion of correct responses as a function of stimulus type and position of target-distracter mismatch are displayed in Figure 6. The factor stimulus type violated sphericity, and so a Greenhouse-Geisser correction was used for the correspondent main effect, which reached significance (F₁ [1.36, 20.45] = 22.14, MSE = .044, p < .001; F₂ [2, 545] = 52.96, MSE = .030, p < .001). Nonwords yielded higher accuracy in responses compared to strings of consonant (t₁ [15] = 3.92, p < .01; t₂ [378] = 6.01, p < .001) and strings of symbols (t₁ [15] = 5.27, p < .001; t₂ [378] = 9.83, p < .001). Accuracy, moreover, was higher in responses to consonant-strings, compared to strings of symbols (t₁ [15] = 4.21, p < .01; t₂ [358] = 3.84, p < .001). The main effect of position of the target-distracter mismatch was significant, (F₁ [4, 60] = 3.78, MSE = .015, p < .01; F₂ [4, 545] = 4.37, MSE = .030, p < .01). More importantly, the stimulus type by position interaction was highly significant (F₁ [8, 120] = 4.12, MSE = .011, p < .001; F₂ [8, 545] = 3.65, MSE = .030, p < .001). The effect of position was significant for nonwords (F₁ [4, 60] = 6.05, MSE = .009, p < .001; F₂ [4, 195] = 5.00, MSE = .028, p < .01), for strings of consonants (F₁ [4, 60] = 4.53, MSE = .017, p < .01; F₂ [4, 175] = 6.16, MSE = .028, p < .001), but not for strings of symbols (F₁ [4, 60] = 1.59, MSE = .014, p > .1; F₂ [4, 175] = 1.27, MSE = .034, p > .2). Planned comparisons between each of the positions within each stimulus type are reported in Table 6. Note that while a significant first position advantage is detected for both nonwords and consonant-strings, no such effect was found for symbols.

Figure 6.

Experiment 3: Mean proportion of correct responses and mean reaction times (RT) as a function of position of the target-distracter mismatch and stimulus-type (nonwords, strings of consonants, strings of symbols). Error bars represent standard error of the mean.

Table 6.

Planned comparisons proportions of correct responses (ACC) and reaction times (RT) between different positions of target-distracter mismatch within each stimulus type (nonwords, strings of consonants, and string of symbols) in Experiment 3.

Stimulus type and positions of mismatch	ACC		RT
	t1	t2	t1	t2
Nonwords
1 vs. 2	2.86*	2.64**	−3.27**	−3.78***
1 vs. 3	2.58*	2.29**	−3.19**	−3.80***
1 vs. 4	4.62***	3.47***	−4.41**	−4.32***
1 vs. 5	4.54***	4.22***	−4.12**	−4.62***
2 vs. 3	−.35	−.33	−.44	−.39
2 vs. 4	.85	.86	−.68	−.48
2 vs. 5	1.40	1.60	−1.35	−1.07
3 vs. 4	1.69	1.19	.14	−.05
3 vs. 5	2.42*	1.92°	−.49	−.64
4 vs. 5	.79	.73	−.87	−.63
Strings of consonants
1 vs. 2	1.87°	2.30*	−3.34**	−2.51*
1 vs. 3	3.48**	4.38***	−2.65*	−3.58**
1 vs. 4	2.99**	3.37**	−3.17**	−3.62**
1 vs. 5	2.10°	2.43*	−3.26**	−3.67***
2 vs. 3	2.05°	2.83**	−.46	−.99
2 vs. 4	1.45	1.65	−1.58	−1.30
2 vs. 5	.51	.49	−1.47	−1.12
3 vs. 4	−.71	−.85	−1.35	−.38
3 vs. 5	−1.63	−1.94°	−.55	−.14
4 vs. 5	−.99	−1.01	.56	.25
Strings of symbols
1 vs. 2	−2.72*	−1.90	−.50	−.43
1 vs. 3	−1.78°	−1.46	−.45	.64
1 vs. 4	−1.27	−1.02	−.74	.65
1 vs. 5	−.35	−.38	−1.15	.17
2 vs. 3	.41	.35	−.13	1.12
2 vs. 4	.92	.84	−.52	1.06
2 vs. 5	1.67	1.69°	−1.1	.60
3 vs. 4	.55	.45	−.77	.11
3 vs. 5	1.25	1.20	−1.04	−.45
4 vs. 5	.75	.73	−.47	−.49

Note. t₁ refers to paired-sample t-test conducted within participants. t₂ refers to independent-sample t-test conducted between items.

^***p < .001;

^**p < .01;

^*p < .05;

^°p < .1. Results, in terms of significance, were the same across analyses on raw accuracies/response latencies and arcsine-root-transformed accuracies/z-score-transformed response latencies, except where marked (^{^}).

4.2.2 Response latencies

Mean RTs as a function of stimulus type and position of the mismatch between target and distracter are displayed in Figure 6. The main effect of stimulus type was significant only in the analysis by items (F₁ < 1; F₂ [2, 544] = 3.95, MSE = 62320.7, p < .05). The effect of position of the target-distracter mismatch (where a Greenhouse-Geisser correction was applied, given the violation of sphericity) was significant (F₁ [2.27, 34.12] = 5.19, MSE = 60821.18, p < .01; F₂ [4, 544] = 4.07, MSE = 62320.7, p < .01), and the interaction reached significance only in the analysis by-items (F₁ < 1; F₂ [8, 544] = 1.96, MSE = 62320.7, p < .05). The effect of position was significant for nonwords (F1 [4, 60] = 6.22, MSE = 12606.42, p < .001; F₂ [4, 195] = 6.17, MSE = 30729.78, p < .001), and strings of consonants (F₁ [4, 60] = 4.87, MSE = 23901.98, p < .01; F₂ [4, 175] = 4.20, MSE = 66426.67, p < .001), but not for strings of symbols (Fs < 1). Planned comparisons between each of the positions of target-distracter mismatch within each type of stimuli are reported in Table 6. Note that the first position advantage appears quite reliable for stimuli made of letters (i.e., for nonwords and strings of consonant), but not for strings of symbols.

4.3 Discussion

When legal nonwords, strings of consonants, and stings of symbols were presented randomly intermixed, a first-position advantage was found only for stimuli made of letters, suggesting that the initial letter advantage was not due to the lexical characteristics of Experiments 1 and 2, but is specific to letter stimuli. This pattern is consistent with the results of Tydgat and Grainger (2009) and Grainger, Tydgat, and Isselé (2010) and extends their results beyond a single letter identification paradigm. However, it is again noteworthy that there was no advantage for the mismatch at fixation in this study as observed in these previous studies. Before turning to a discussion of these results, it is important to note that overall performance on strings of symbols was relatively low in Experiment 3, and this may have obscured the opportunity to observe a first position effect. To investigate this possibility, in Experiment 4, we increased the duration of the stimuli (83 ms, compared to the previous 33 ms of exposure) to determine if there is any evidence of an initial position effect when performance is in a more sensitive range.

5. Experiment 4

5.1 Method

5.1.1 Participants

Twenty-four undergraduate students participated to the experiment for course credit or compensation ($5). All were native English speakers and reported normal or corrected-to-normal vision.

5.1.2 Materials

The same strings of symbols used in Experiment 3 were used in the present experiment.

5.1.3 Apparatus and procedure

Apparatus and procedure were the same as in previous experiments. The only difference was that the duration of the target was increased to 83 ms. Participants were presented only with strings of symbols, for a total of 90 trials (18 trials for each of the five positions of target-distracter mismatch). After 45 trials, participants were prompted to take a short break and received feedback on their proportion of correct responses. Participants received 10 practice trials with strings of symbols, as in Experiment 3. The experimental session lasted about 20 minutes.

5.2 Results

In order to insure that performance is at comparable levels to Experiment 3 letter string conditions, the 4 participants with lowest overall accuracy were also eliminated from the analyses.³ It is conceivable that any eventual first position advantage might be obscured by an overall high rate of guessing. In an effort to minimize this possibility, we also report the analyses performed on the subset of 12 participants (determined via median split) who showed the highest overall accuracy (high accuracy participants). The overall mean of proportion of correct responses for this latter group ranged from .60 to .75 (mean = .66, SD = .05). Note that the overall performance for 10 out of this subset of 12 participants was significantly above chance (all χ²s > 4.44, all ps < .05). For the other two participants, the difference between their performance and a chance-level one was closely approaching the conventional level of significance (both χ²s = 3.6, ps = .06). Clearly, the performance of high accuracy participants is comparable, in terms of accuracy, to the one detected in Experiment 3 for strings of consonants (the mean proportion of correct responses for this latter stimuli was .61, SD = .06).

Trials in which an error occurred in timing of the visual display (0.17%) were removed from all the following analyses. For the analysis of response latencies, errors (38.45% when considering all participants, 33.55% when considering high accuracy participants) were excluded. There were no correct trials below 200 ms, and so no trials were removed based on this criterion. Trials in which the RTs were 2.5 SD from the participant’s mean were considered outliers and removed from the analysis. These trials represented 1.81% of the total when considering all participants. When considering high accuracy participants, based on the same criterion, 2.51% of the trials were identified as outliers and removed from the RT-analyses.

5.2.1 Accuracy

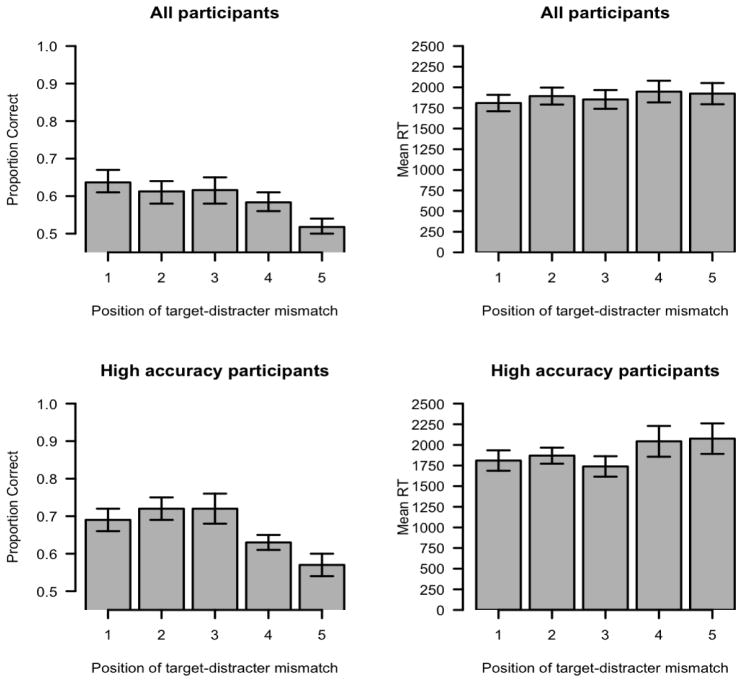
Accuracy as a function of position is displayed in Figure 7. In the following analyses, given the violation of the sphericity assumption, the Greenhouse-Geisser correction was applied. Considering all participants, the effect of position was significant, (F₁ [2.47, 46.91] = 3.49, MSE = .027, p < .05; F₂ [4, 175] = 3.57, MSE = .03, p < .01). Importantly, in contrast to the previous first position advantage, planned comparisons indicated that the last position produced a disadvantage compared to all the other positions, and there is no evidence of a significant first position advantage (see Table 7). Similar results were found when restricting the analyses to high accuracy participants. The effect of position was significant (F1 [2.26, 24.87] = 3.59, MSE = .023, p < .05; F2 [4, 175] = 3.02, MSE = .056, p < .05) and planned contrast reveled again a disadvantage for last position, and no advantage for first position (see Table 7).

Figure 7.

Experiment 4: Mean proportion of correct responses and reaction times (RT) as a function of position of the target-distracter mismatch for all participants and for high accuracy participants. Error bars represent standard error of the mean.

Table 7.

Planned comparisons for proportions of correct responses (ACC) and reaction times (RT) between different positions of target-distracter mismatch for the two groups of participants (Group) considered within in Experiment 4.

Group	Position of mismatch	ACC		RT
		t1	t2	t1	t2
All participants
	1 vs. 2	.30	.47	−1.47	−.01
	1 vs. 3	.31	.53	−.52	.48
	1 vs. 4	1.70	1.63	−2.45*	−2.28*
	1 vs. 5	3.29**	3.37**	−2.23*	−1.03^
	2 vs. 3	.09	.01	.70	.48
	2 vs. 4	1.18	1.08	−.94	−2.24*^
	2 vs. 5	4.33***	2.73**	−.80	−1.01
	3 vs. 4	1.17	1.17	−1.56	−2.77*
	3 vs. 5	3.10**	2.98**	−1.33	−1.49^
	4 vs. 5	2.10°	1.71°	.16	1.16
High accuracy participants
	1 vs. 2	−.59	−.30	−.70	−.27
	1 vs. 3	−.46	−.51	.61	1.62
	1 vs. 4	1.11	1.03	−2.00°	−2.06*
	1 vs. 5	2.06°	2.80**	−2.40*	−1.79°
	2 vs. 3	.00	−.22	1.51	1.91°
	2 vs. 4	2.22*	1.27	−1.27	−1.87°^
	2 vs. 5	4.91***	3.03**	−1.50	−1.60
	3 vs. 4	3.08**	1.42	−2.49**	−3.44**
	3 vs. 5	3.31**	3.12**	−2.73**	−3.09**
	4 vs. 5	1.52	1.28	−.70	.10

Note. t₁ refers to paired-sample t-test conducted within participants. t₂ refers to independent-sample t-test conducted between items.

^***p < .001;

^**p < .01;

^*p < .05;

^°p < .1. Results, in terms of significance, were the same across analyses on raw accuracies/response latencies and arcsine-root-transformed accuracies/z-score-transformed response latencies, except where marked (^{^}).

5.2.2 Response latencies

Mean RTs as a function of position are plotted in Figure 7. Greenhouse correction was applied in the following analyses. Considering all participants, the effect of position did not reach significance in the analysis by participants (F₁ [2.48, 47.06] = 1.94, MSE = 112727.5, p > .14), but was significant in the analysis by items (F₂ [4, 175] = 2.47, MSE = 141740.77, p < .05). Planned comparisons are listed in Table 7, which clearly does not indicate the strong step function for the first position that was found in the previous experiments. Similarly, when considering high accuracy participants, the effect of position was significant (F1 [2.21, 23.34] = 3.47, MSE = 134493.06, p < .05; F2 [4, 175] = 4.24, MSE = 214520.26, p < .01). Planned comparisons suggest that RTs increase in last positions, but again the strong step function found in previous experiments for first position is absent (See Table 7).

5.3 Discussion

The results from Experiment 4 indicated that even when only strings of symbols are displayed and the time of exposure is increased from 33 to 83 ms, there is no first position advantage, even when noise from guessing is minimized by restricting the analyses to those participants displaying the higher accuracy, who were arguably relying less on guessing to give their responses. Indeed the results indicated a last position disadvantage in accuracy. Thus, these results converge with the results from Experiment 3 that the first position advantage with this paradigm appears to be letter specific.

6. General Discussion

Across a series of four experiments, a first position advantage was reliably detected both in terms of accuracy and response latency when the stimuli involved words, legal nonwords, and random consonant strings, but not non-alphabetic symbols, suggesting that the effect is pre-lexical and occurs specifically and selectively for letters. Moreover, the first position advantage for words was shown to occur across stimuli of different lengths and when the length of the stimulus was blocked vs. randomly intermixed, thus providing evidence for its robustness and generalizability. These data extend those of Adelman et al. in three ways. First, the present results suggest that the first position advantage is reliable across words of different lengths (ranging from form three-letter words to six-letter words), even when these differences in length are unpredictably distributed within the same experiment. Second, the present experiments extend the analyses of the phenomenon to RTs, suggesting that information regarding the first position becomes available relatively earlier than other positions. Finally, the first-position advantage, both in terms of accuracy and RTs, was reliably detected for legal nonwords (thus replicating data reported by Gomez et al., 2008, even with shorter stimulus durations) and for strings of consonants where, arguably, no lexical activation is available. Importantly, no evidence for a first position advantage was detected in strings made of symbols, neither at the short stimulus duration with which other stimuli were investigated (i.e., 33 ms), nor when stimulus duration was considerably increased (Experiment 4). This suggests that the phenomenon, although independent of lexical constraint, occurs specifically for letters and it’s not just a perceptual property of visual objects displayed in horizontal arrays.

The parallel between our results and previous studies of serial position effects in letter-identification is partial. More specifically, the present results primarily showed a substantial first position advantage, whereas previous studies involving letter identification as the primary dependent variable have also found an advantage of the last position and for the letters at fixation (e.g.., Mason, 1982; Merikle, Coltheart, & Lowe, 1971; Merikle, Lowe, & Coltheart, 1971; Mewhort & Campbell, 1978; Tydgat & Grainger, 2009). The differences in results are likely due to differences in experimental paradigms employed. For example, in their recent investigations, Tydgat and Grainger (2009) used a two-alternative forced choice task (akin to the classic Reicher, 1969 and Wheeler, 1970, studies), in which the two alternative responses consisted of single letters after a target string was displayed for 100 ms between both a forward and a backward mask (see their Experiment 4 for a partial report procedure producing the same patter of results). The first obvious difference with respect to the experiments presented here is the duration of the stimuli (33 ms. here, 100 ms in Tydgat & Grainger, 2009). However, it is unlikely that differences in our results can be explained just in terms of duration of the stimuli, given previous findings of an advantage for the letter at fixation even with stimuli presented for 30 ms (Merikle, Coltheart, & Lowe, 1971). A second important difference lies in the task itself. Of course, the 2-alternative forced choice task on single letters is most consistent with the standard word superiority paradigm while the present experimental paradigm may engage alternative strategies. For example, participants might perform a left-to-right serial comparison between the letters of the two response alternatives and the letters of the stored representation of the previously displayed target. This would not only predict an advantage for the leftmost character, but also a left to right linear decrement in accuracy, paralleled by an increase in RTs. However, although a linear decrease in accuracy is present in our data, this is clearly not comparable with the progressive drops in accuracy as a function of left-to-right serial position detected in those tasks which actually require a letter by letter, left-to-right report (e.g., Merikle, Coltheart, & Lowe, 1971). More importantly, if our results simply reflect a left to right scan, then one would have expected this to occur even for arrays made of symbols. Hence, our data offer evidence more consistent with a selective, letter-specific first position advantage, as opposed to a more general task-induced left-to-right scanning process.

It is interesting to note that, even in more traditional paradigms, the first position advantage appears the most selective and the most pervasive finding. It is highly selective, in the sense that it occurs just when the target-arrays are made of letters, but not when the displays are made of symbols (Mason, 1982; Tydgat & Grainger, 2009). The advantage for items at fixation, on the other hand, reliably appears for both classes of stimuli. Thus, the fixation advantage may be more related to visual acuity at fixation. Moreover, the first position advantage is also the most pervasive finding because the analogous advantage for the final letter appears to be particularly sensitive to visual interference. For example, in Tydgat and Grainger’s (2009) experiments, the final position advantage was not present when the 2 single-letter alternative responses were presented near the final letter, but was present when the alternative responses were displayed further away from the last position. On the other hand, the first position advantage reliably appeared throughout all the experiments, regardless of the proximity of the response alternatives. Hence, although the better performance in detecting the letters in last position might simply represent a byproduct of the reduced visual interference from a flanking character, the first position advantage does not appear to be simply due to this flanking effect. Indeed, the robustness and selective nature of the first-position advantage might suggest that this effect is likely to influence not just letter detection tasks, but reading (intended as whole word recognition) as well.

In this light it is interesting to note that the first position advantage detected in the present experiments is in large part consistent with a series of well-known effects within the eye-tracking literature. For example, readers tend to fixate slightly at the left of the middle of the words (e.g., Nazir, Jacobs, & O’Regan, 1998; Rayner, 1979). Such a preferred viewing location (Rayner, 1979) would be chosen because initial letters are more informative about the lexical identity of the target-word (Clark & O’Regan, 1999; see also Stevens & Grainger, 2003). Readers are also able to obtain parafoveal information from a word placed at right of fixation -a phenomenon known as parafoveal preview (see Rayner, 1998)- and to use this information to aid the recognition of the parafoveal word when it is later fixated. Critically, the first two letters are most important in this phenomenon (e.g., Balota & Rayner, 1983; Lima & Inhoff, 1985; Rayner, McConkie, & Zola, 1980; Rayner, Well, Pollatsek, & Bertera, 1982).

Interestingly, there is a recent study of sentence reading that also provides support for the special nature of first letter processing compared to all other positions. Johnson and Eisler (2012) found that letter-transpositions within words embedded in sentences (e.g., judge - jugde) disrupt reading more when it occurs for letters in first or in final positions compared to when it involves internal letters (see also White, Johnson, Liversedge, & Rayner, 2008). Crucially, when letters in all positions are equated in terms of the degree of lateral visual interference received from adjacent characters (e.g., by having spaces replaced with hash marks), transpositions involving first-position still disrupt processing more than internal transposition, whereas there is no longer the difference between last letter transpositions and internal transpositions. Note that the pattern is the same even when reading words in a right to left sequence (see Johnson & Eisler, 2012). This stands as further evidence that while the special status of the final letter originates from the absence of lateral interference from an adjacent character to the right, letters in the first position benefit from additional unique mechanisms.

This special advantage of the first position also is consistent with two specific computational instantiations of letter coding referred to as the Overlap Model (Gomez et al., 2008) and the Letters in Time and Retinotopic Space model (LTRS; Adelman, 2011). According to the former, letter identities are assumed to be normally distributed over positions. Any given letter is not only associated just with its specific position (e.g., a, in the word trail, with third position) but also with other surrounding positions. Each position has a different standard deviation. In order to accommodate the first letter advantage, Gomez et al. argued that the SD associated with the first position is smaller compared to all other positions, thus producing more efficient coding for those letters occurring in that position. In the LTRS model, letter identification is implemented as a piecemeal process where discrete units of information are processed over time, rather than as a process of graded matching with stored lexical representations. Critically, although processing for all the letters starts at the same time, processing strengths vary as a function of the position of the specific letter within the array. This feature enables the model to capture first-position advantage phenomena by assigning higher values of processing strength to the first letter. Hence, both of these computational models claim that processing for letters in first position is further qualified by unique advantages (albeit somewhat different mechanisms), compared to other letter positions.

Although the models discussed above are models of letter coding, one might ask whether the first position advantage can be reconciled with traditional modeling frameworks of word-recognition. For example Rumelhart and McClelland (1982), in their Interactive Activation Model, addressed the issue of asymmetrical serial position functions in letter identification by implementing differential input rates for letters as a function of position (with the highest rate assigned to first position). A recent extension of the Interactive Activation (IA) framework is represented by Davis’ (2010) Spatial Coding Model. In line with the IA framework, the Spatial Coding model has distinct representational levels for features, letters and words (plus an intermediate level of units that connect letters to words), each one characterized by a localist representation. Letter order is encoded via the assignment of a temporary and purely positional value to each letter. Such values are described by Gaussian functions, and the SDs of these functions reflect position uncertainty, while their amplitude is related to the amount of information regarding a specific letter’s identity. Word recognition is accomplished via superimposition matching between the spatial code of the stimulus presented (signal) to the model and the spatial code of the stored lexical representation (weight). Critically, letter-level is specifically equipped with exterior letter banks that code the initial and final letters of the stimulus. The weights of the connections between letter-banks and a given word can vary across letter banks, so that greater weights can be assigned to those letters that are perceptually more salient. Note that the model implements similar processing assumptions for both the letters in the first and last positions. However, our data, as well as data from recent other studies (e.g., Johnson & Eisler, 2012; Tydgat & Grainger, 2009), suggest that there are important differences between first and last position letter processing. In fact, first-position advantage reliably occurs in paradigms were no hint of a correspondent last-position advantage appears, as in the present experiments. Moreover, factors that eliminate the last position advantage (such as an increased visual interference, e.g., Johnson & Eisler, 2012, Tydgat & Grainger, 2009) do not seem to influence the first-position advantage to a comparable extent. Taken together, this evidence suggests that important qualitative differences may occur between first and last letter processing and that any apparently similar processing advantage for the two (when observed) may indeed reflect only partially overlapping mechanisms.

Importantly, one should ask what underlies the development of a first letter position advantage. As noted above, the first letter in words is usually more constraining on lexical identity (Grainger & Jacobs, 1993; see also Friedmann & Givonn, 2001). The importance of the first letter positions in lexical processing should increase the reliance on this position. Importantly, such an increased reliance appears to occur at a relatively early stage of processing. Hence, even if the first-position advantage appears as a pre-lexical effect, it might ultimately reflect an adaptation to a recurrent feature of the lexical environment, i.e., the importance of the first letter.

This proposal is clearly consistent with the arguments by Tydgat and Grainger (2008; see also Grainger, Tydgat, & Issele, 2010), regarding the “modified receptive fields hypothesis” (Chanceaux & Grainger, 2012). According to this hypothesis, the system adapts the size and the shape of receptive field for letters, in order to optimize the efficiency of processing in a highly crowded environment (i.e., the reading environment). Receptive fields for letters are small, in order to suffer less interference from flanking characters. Moreover, in order to enhance the efficiency of processing for letters in first position, the authors assume the receptive field is elongated to the left. Assuming a constant surface for receptive fields in a given eccentricity, this leftward elongation implies a reduction of their rightward extension (Chanceaux & Grainger, 2012). Clearly, given the absence of any character to the left of the first letter, this shape would minimize the interference from the only flanking character, i.e. the character to the right of the first letter. Interestingly, as noted by Chanceaux and Grainger (2012), similar ideas have been recently implemented in the SERIOL2 model (Whitney, 2011), which incorporates retinotopic letter detectors. The previous SERIOL model (Whitney, 2001) would predict similar serial position functions across all visual objects. However, the notion of specific letter detectors whose size and shape varies as a function of eccentricity and visual field enables the model to account for the dissociations between letters and other visual objects (e.g., non alphabetical symbols), consistent with the current results.

5.1 Conclusions

In summary, the present experiments clearly provide a rather dramatic demonstration of first letter processing advantage that extends to strings of different length, words, pronounceable nonwords and unpronounceable nonwords. Crucially, this phenomenon appears to selectively affect letters, and not to be a general property of horizontal arrays of visual objects. As such, the present experiments provide important evidence supporting those models and theories that maintain specific processing features for letters in the first position. The convergence across multiple paradigms for this first letter advantage clearly poses some challenge for the argument that letters are processed equally and in parallel in early stages of reading, which is the modus operandi of current models of visual word recognition. Moreover when parallel models capture the first-position advantage, additional assumptions are made, which do not capture the powerful specificity of the first position advantage.

Highlights.

1. We investigated serial position functions for letter recognition in a perceptual matching task.

2. A processing advantage is found in terms of accuracy and latency for letters in first position.

3. This finding was consistent across words, nonwords and random consonants, but not with symbols.

4. This pattern is discussed with respect to findings from other paradigms.

5. Results support models that maintain special features for processing letters in first position.