Background: “Humanized” mutants of bacterial dihydrofolate reductase were examined to relate protein dynamics with enzyme evolution.
Results: Effects on enzyme dynamics alter the catalyzed C-H→C step, but the nature of that step was retained along evolution.
Conclusion: Protein dynamics evolved to optimize the catalyzed reaction.
Significance: Evolutionary conservation of functional dynamics implicates their role in the catalyzed hydride transfer reaction.
Keywords: Enzyme Catalysis, Enzyme Kinetics, Enzyme Mutation, Enzymes, Isotope Effects, Protein Dynamics, Protein Evolution, Marcus-like, Dihydofolate Reductase, Enzyme Dynamics
Abstract
The hydride transfer reaction catalyzed by dihydrofolate reductase (DHFR) is a model for examining how protein dynamics contribute to enzymatic function. The relationship between functional motions and enzyme evolution has attracted significant attention. Recent studies on N23PP Escherichia coli DHFR (ecDHFR) mutant, designed to resemble parts of the human enzyme, indicated a reduced single turnover rate. NMR relaxation dispersion experiments with that enzyme showed rigidification of millisecond Met-20 loop motions (Bhabha, G., Lee, J., Ekiert, D. C., Gam, J., Wilson, I. A., Dyson, H. J., Benkovic, S. J., and Wright, P. E. (2011) Science 332, 234–238). A more recent study of this mutant, however, indicated that fast motions along the reaction coordinate are actually more dispersed than for wild-type ecDHFR (WT). Furthermore, a double mutant (N23PP/G51PEKN) that better mimics the human enzyme seems to restore both the single turnover rates and narrow distribution of fast dynamics (Liu, C. T., Hanoian, P., French, T. H., Hammes-Schiffer, S., and Benkovic, S. J. (2013) Proc. Natl. Acad. Sci. U.S.A. 110, 10159–11064). Here, we measured intrinsic kinetic isotope effects for both N23PP and N23PP/G51PEKN double mutant DHFRs over a temperature range. The findings indicate that although the C-H→C transfer and dynamics along the reaction coordinate are impaired in the altered N23PP mutant, both seem to be restored in the N23PP/G51PEKN double mutant. This indicates that the evolution of G51PEKN, although remote from the Met-20 loop, alleviated the loop rigidification that would have been caused by N23PP, enabling WT-like H-tunneling. The correlation between the calculated dynamics, the nature of C-H→C transfer, and a phylogenetic analysis of DHFR sequences are consistent with evolutionary preservation of the protein dynamics to enable H-tunneling from well reorganized active sites.
Introduction
Significant advancements have been achieved toward characterizing protein motions across wide ranging time scales, from seconds to femtoseconds, and investigating their functional relevance. The importance of protein motions on the milli- to microsecond time scale is recognized to affect substrate binding and product release, often contributing to the rate-limiting step during catalytic turnover (1). However, the precise role of the protein motions in assisting chemical transformations has remained unclear and is highly debated. Elucidating the role of the protein motions is crucial to understanding enzyme mechanisms, and such knowledge may also assist in widening the applicability of enzymes in industrial and medicinal settings.
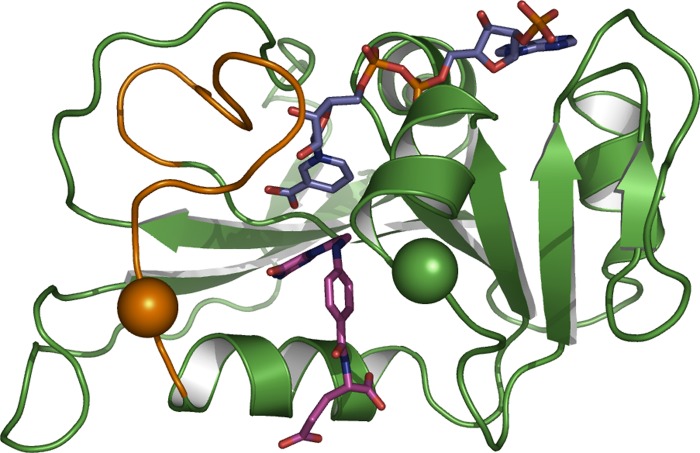
Escherichia coli dihydrofolate reductase (ecDHFR)3 is a model system used to address the link between enzyme dynamics and function (Scheme 1) (2–15). DHFRs catalyze the stereospecific reduction of 7,8-dihydrofolate to 5,6,7,8-tetrahydrofolate through a transfer of a pro-R hydride from the C4 position of reduced NADPH to the C6 atom of the dihydropterin ring of 7,8-dihydrofolate (Fig. 1). ecDHFR has an α/β structure with a core of eight-stranded β-sheets and four α-helices that are connected by several loop regions (16). Of these, the flexible Met-20 loop (residues 9–24) undergoes extensive conformational changes during the catalytic cycle (Fig. 2) (16–18). The catalytic turnover of ecDHFR is rate-limited by product release for kcat (12 s−1 at pH 7 and 25 °C) (19) or more precisely by a conformational change prior to product release (20). The single turnover rate (kH from pre-steady-state kinetics; 200–230 s−1 at pH 7 and 25 °C), on the other hand, seems to be limited by loop closure and flipping of the nicotinamide ring into the active site (17, 21, 22).
SCHEME 1.
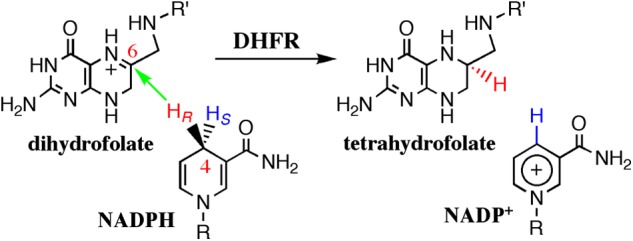
The reaction catalyzed by ecDHFR. R indicates adenine dinucleotide 2′-phosphate, and R′ indicates (p-aminobenzoyl) glutamate. It was shown previously that the protonation of the N5 position occurs prior to hydride transfer (6, 36, 37).
FIGURE 1.
Structure of ecDHFR (Protein Data Bank code 1RX2). The Met-20 loop is shown in brown, folate is shown in purple, and the nicoinamide ring of NADPH is in blue. Residues Asn-23 and Gly-51 are shown as brown and green spheres, respectively.
FIGURE 2.
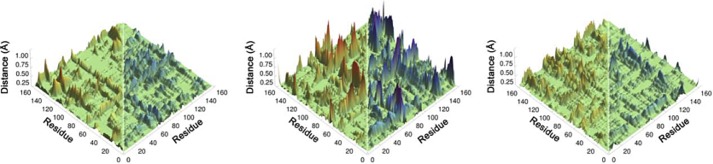
Computed thermally averaged α-carbons distance changes from the reactant state to the transition state for all pairs of residues in ecDHFR (left), the N23PP mutant (middle), and the N23PP/G51PEKN mutant (right). Distances that increase from the RS to the TS are colored red (0 to 0.75 Å), and distances that decrease from the RS to the TS are colored blue (0 to −0.75 Å). Although each matrix is symmetrical, for clarity only distances that increase are shown on the left side and distances that decrease are shown on the right (from Ref. 24, with permission from the National Academy of Science).
X-ray crystallography and NMR studies indicated motions of the Met-20 loop and other protein motifs along the catalytic cycle of the enzyme (16, 17). For example, the Met-20 loop exists in a closed conformation in the Michaelis complex (E·NADPH·7,8-dihydrofolate), where it is closely packed against the nicotinamide ring of the cofactor. After hydride transfer occurs, the Met-20 loop initially opens to allow the nicotinamide-adenosyl moiety of the cofactor to rotate out of the active site, after which it adopts the occluded conformation. In this conformation, observed in the product complex by x-ray and NMR analysis, the Met-20 loop extends into the active site, blocking the nicationamide binding pocket (16–18). Human DHFR catalyzes the same reaction as the bacterial enzyme; however, crystal structures of both its binary and ternary complexes show solely closed confirmation of the Met-20 loop, which might suggest that it spends more time in that conformation during the catalytic cycle (Protein Data Bank codes 2W3M, 2W3A, 4DDR, 3S7A, and 1YHO).
Analysis of DHFR sequences from 233 species ranging from Escherichia coli to humans identified phylogenetically coherent events (24). These evolutionarily significant divergence sites include a polyproline sequence (PWPP) in the Met-20 loop region of the enzyme (position Asn-23 in ecDHFR; brown sphere in Fig. 2) that is found only in higher organisms. In addition, a four amino acid insertion (PEKN) was introduced early in the evolution of the enzyme and is highly conserved in higher organisms. Importantly, all DHFR sequences containing the polyproline sequence at Asn-23 also always have the insertion at Gly-51, indicating that no DHFR in nature ever evolved to have the Asn-23 insertion unless it also had the Gly-51 insertion.
In 2011, Bhabha et al. (3) studied the possible correlation between millisecond Met-20 loop motions (examined via NMR relaxation experiments) and the steady-state and single turnover rate using three mutants of ecDHFR: N23PP, S148A, and N23PP/S148A. The ecDHFR variants N23PP/S148A and N23PP (the S148A mutation seems to have little or no effect) were named “dynamic knock-out” mutants, due to their rigidified Met-20 loop. NMR results suggested that millisecond time scale fluctuations in the active site of WT ecDHFR are similarly reduced in the N23PP as in N23PP/S148A mutants, whereas the x-ray structure of the relevant ternary complex suggested that these mutations had no effect on the structure of the active site. Moreover, the addition of the bi-proline sequence significantly reduced the steady-state and single turnover rates relative to the WT.
Kinetic isotope effects (KIEs) are the ratio of rates for light versus heavy isotopologues, i.e. reactants that only differ in their isotopic composition. For example, the ratio of the rate for protonated substrate versus deuterated substrate is annotated as H/D KIE.
Although the observed H/D KIEs at 25 °C were the same for N23PP and the WT, the NMR relaxation experiments indicated that altered millisecond timescale motions affect the kH rate, and thus it was suggested it might be directly coupled to the H-transfer (3). This interpretation was recently challenged by theoretical (2) and experimental (8) studies. Importantly, changes in reorganization energy caused the depressed catalytic effects, as empirical valence bond calculations imply (2). Notably, motions along the slow conformational coordinate, which were examined by the NMR relaxation experiments (3), have a substantial effect on the steady-state and single turnover rate but might not be coupled to the much faster chemical step (dissociation of the C-H bond at femto- picosecond time scale) (4).
Kinetic studies of a double mutant, N23PP/G51PEKN, showed that the insertion of PEKN restored both the steady-state and single turnover rates of N23PP to that of the WT. Importantly, QM/MM simulations (24) indicated that on the fs-ns time scale the N23PP ecDHFR has a much broader range of dynamics (i.e. less “rigid”) when going from the reactant state to the transition state than the WT. These calculations also indicated a restoration of narrower dynamics distribution for the N23PP/G51PEKN double mutant to a level similar to that of the WT (Fig. 3) (24). Yet, all of the rates and KIEs (e.g. kH, kcat, and kcat/Km) examined by these studies reflect complex rate expressions composed of several microscopic rate constants (19, 20), prohibiting assessment of the effect of the altered and restored dynamics on the catalyzed H-transfer.
FIGURE 3.
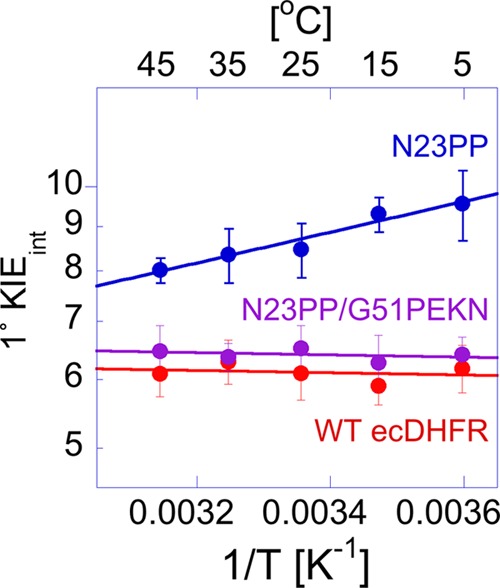
Arrhenius plot of the intrinsic H/T KIEs of on the hydride transfer reaction catalyzed by WT (red) (12) N23PP/G51PEKN (purple), N23PP (blue), and ecDHFR (red). The data points are the average of at least five independent measurements with their S.D., and the lines are nonlinear fits of all measured KIEs to the Arrhenius equation.
The main experimental method used here is the examination of the temperature dependence of intrinsic KIEs. This method has been previously used extensively for ecDHFR and its mutants (8, 9, 12–14) and many other enzymes (25–29). The advantage of this experimental method is that the temperature dependence of KIEs is highly sensitive to the changes in the hydrogen donor and acceptor distance (DAD), which can modulate the degree of the nuclear wave function overlap between the donor and acceptor states of the hydride being transferred (27, 30). As suggested by several phenomenological models, referred to here as Marcus-like models, temperature-independent KIEs indicate a short and narrow distribution of DADs, whereas temperature-dependent KIEs are associated with longer and broader DAD distributions with lower fluctuation frequency (27, 31–34). QM/MM calculations have confirmed that the DAD is the dominant factor in determining the temperature dependence of the KIE in ecDHFR (6, 7, 10, 28). Marcus-like models have been used to explain C-H bond activation in many enzymes (9, 12–14, 25–29, 32–38), where it has been found that most wild-type enzymes with their natural substrates have well reorganized active sites, whereas many mutants or enzymes under non-physiological conditions do not.
In the current study, we examined the temperature dependence of the intrinsic KIEs for both N23PP and N23PP/G51PEKN and compared these data to previous findings with these mutants and the WT ecDHFR. Experimental and theoretical studies of the temperature dependence of KIEs in a variety of enzymatic systems suggested that fast dynamics of the reactive complex directly affect the reaction coordinate (25, 27, 38, 39). It is important to note that in this study, the term “dynamics” refers to only these fast motions of the active site that directly affect the catalyzed hydride transfer. Our findings for N23PP indicate a poorly reorganized tunneling ready state (TRS), which is restored to that of the native enzyme after addition of the PEKN mutation. These findings imply that dynamics faster than the millisecond motions examined by NMR (3) are also altered in N23PP and restored in the N23PP/G51PEKN double mutant and that those faster dynamics and their effect on the catalyzed C-H→C transfer are evolutionary preserved. The last conclusion is supported by the observation that Asn-23 insertion only occurs in organisms that already have the Gly-51 insertion.
MATERIALS AND METHODS
Materials
[Ad-14C]-NAD+ (specific radioactivity of >220 mCi/mmol) was from PerkinElmer Life Science. Dihydrofolate was prepared by dithionate reduction of folic acid as described previously (40). Glucose dehydrogenase from Bacillus megaterium was from Affymetrix/USB. All other enzymes for synthesis of radiolabeled substrates were from Sigma-Aldrich. (R)-[4-3H]-NADPH and [Ad-14C]-NADPH were synthesized as described (30, 41). All synthesized materials were purified and stored as described previously (42). N23PP and N23PP/G51PEKN ecDHFR were expressed and purified as described previously (3, 24).
Kinetic Isotope Effect Measurements
KIEs were measured as described for the WT and several mutants of ecDHFR (13, 14, 43). Briefly, purified (R)-[4-3H]-NADPH and [Ad-14C]-NADPH (H/T) or (R)-[4-3H]-NADPH and (R)-[Ad-14C,4-2H]-NADPH (D/T) were combined in the 5:1 3H/14C ratio to measure H/T and D/T primary (1°) KIEs, respectively. Each mixture was co-purified using reverse phase HPLC, divided into aliquots containing at least 300,000 dpm of 14C, and frozen in liquid nitrogen for short term storage at −80 °C. KIE measurements were carried out in MTEN buffer (50 mm MES, 25 mm Tris, 25 mm ethanolamnine, and 100 mm NaCl) at pH 9.0 between 5–45 °C. Reaction mixtures contained a 200-fold excess of dihydrofolate (0.85 mm) over NADPH (4 μm). The reactions were quenched by methotrexate and immediately frozen on dry ice prior to HPLC analysis using the methods described in Ref. 14. Before the analysis, samples were thawed and bubbled with oxygen for 12 min to oxidize the 5,6,7,8-tetrahydrofolate product. The reaction mixture was then resolved by reverse phase HPLC using a method described previously (42) and counted by liquid scintillation analysis. The observed KIEs were calculated using Equation 1 (44),
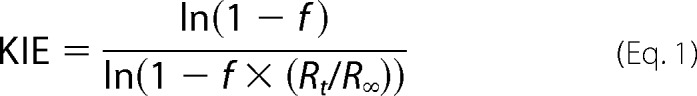 |
where the ratio of 14C in the product and reactant determined the fractional conversion (f), and Rt and R∞ are the ratio of 3H/14C at each time point and at infinite time, respectively.
Determination of the Intrinsic KIEs
Intrinsic KIEs were calculated as described previously (13, 14, 43), using a numerical solution of the modified Northrop equation (43, 45),
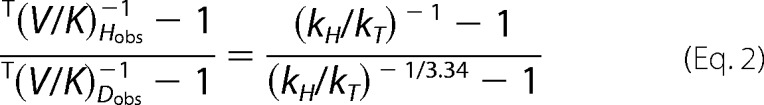 |
where T(V/K)Hobs and T(V/K)Dobs are the observed H/T and D/T KIEs, respectively, and kH/kT represents the intrinsic H/T KIE. The intrinsic KIEs were calculated from all possible combinations of observed H/T and D/T values. Isotope effects on the activation parameters for the intrinsic KIEs were calculated through a nonlinear fit of all intrinsic values to the Arrhenius equation for KIEs,
where kl and kh are the rates for light and heavy isotopes, respectively, Al/Ah is the isotope effect on the Arrhenius pre-exponential factor, ΔEah−l is the difference in energy of activation between the two isotopes, R is the gas constant, and T is the absolute temperature.
The competitive KIEs were measured at pH 9.0 to minimize kinetic complexity (see below). These values cannot be compared with observed KIEs measured under pre-steady-state conditions at different pH values 7–9 (3, 8). However, those observed KIEs (pH 7–9) can be compared with the intrinsic KIEs, or at least their temperature dependence, if the latter are pH-independent. This pH independence was expected, given both experimental and theoretical studies (46, 47), suggesting that the protonation of the N5 position of the substrate precedes the hydride transfer under study. Consequently, the commitment to the C-H→C hydride transfer was expected to increase with decreasing pH, as the H-transfer becomes less rate limiting. To verify that prediction, we measured the intrinsic KIEs at pH 9.0 and 7.0 (Table 1). The intrinsic KIEs for the WT are not changed from pH 9.0 to 8.0 but decreased slightly at pH 7.0. Notably, throughout this pH range the intrinsic KIEs are temperature-independent, indicating a well reorganized TRS. Although these differences are only marginally significant (within experimental error), a decrease in intrinsic KIEs indicates a slight reduction in average DAD form pH 8.0 to 7.0, but no change in DAD distribution (temperature-independent KIEs at all pHs). Importantly, the intrinsic KIEs remained temperature-independent at all pHs, which validates the use of these intrinsic KIEs to calculate the temperature dependence of commitments for observed KIEs measured at the 7.0–9.0 pH range.
TABLE 1.
H/T and D/T KIEs for WT ecDHFR at pH 7.0 and 9.0
Calculation of Kinetic Complexities
In most enzymatic reactions, observed KIEs on bond cleavage are generally smaller than their intrinsic values due to the kinetic complexity arising from the multistep nature of catalytic turnover (i.e. substrate binding, product release, conformational/protonation changes, etc.). As amply described in the literature (48, 49), the following equation relates the observed KIE with the intrinsic value on bond cleavage,
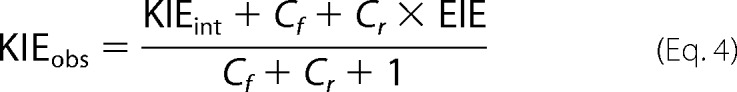 |
where KIEobs is the observed KIE, KIEint is the intrinsic KIE, EIE is the equilibrium isotope effect, and Cf and Cr are the forward and reverse commitments to catalysis, respectively. For the hydride transfer reaction catalyzed by ecDHFR under aerobic conditions, the Cr ≈ 0 and the EIE is close to unity because the reaction is very exothermic, oxygen consumes the product, and the H-isotope is bound to sp3 carbon in both reactant and product states. Therefore, Equation 4 can be simplified to Equation 5,
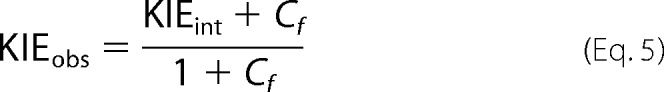 |
where the commitment Cf is the sum of the ratios between the rate of the forward isotopically sensitive hydride transfer step and each of the rates of the preceding backward isotopically insensitive steps (48). Consequently, Cf can be calculated from the observed and intrinsic KIEs obtained from Equations 1 and 2. This commitment is the quantitative measure of kinetic complexity masking intrinsic KIEs for any experimental measurement.
RESULTS
Temperature Dependence of Intrinsic KIEs for WT, N23PP, and N23PP/G51PEKN ecDHFRs
Previous studies showed that the steady-state turnover number (kcat) and single turnover rate (kH) of N23PP were ∼5- and ∼30-fold slower than the WT, respectively (3). As shown in Table 2, the kinetic parameters of N23PP were restored to that of the WT through insertion of G51PEKN (24). To test the effects of the ecDHFR mutants on the nature of the catalyzed hydride transfer, the KIEs on the second-order rate constant (kcat/Km) for N23PP and N23PP/G51PEKN were measured for both H/T and D/T KIEs, and the resulting data were used to calculate the intrinsic KIEs. As shown in Fig. 4 and Table 2, the intrinsic KIEs for N23PP/G51PEKN ecDHFR are, within experimental error, identical to the WT both in magnitude and temperature dependence. These results contrast those observed for the N23PP mutant, which showed temperature dependent intrinsic KIEs. This last result appears to be different than that of Refs. 3 and 8, which reported that the N23PP mutant presents the same observed KIEs for the experimental temperature range on the single turnover rate (kH) as WT. As discussed below, the reason for this apparent difference stems from the kinetic complexity on kH, which masked the differences in the intrinsic KIEs between the WT and N23PP.
TABLE 2.
Comparison of the rates, intrinsic KIEs, and the isotope effects on their activation parameters for WT, N23PP, and N23PP/G51PEKN ecDHFR
FIGURE 4.
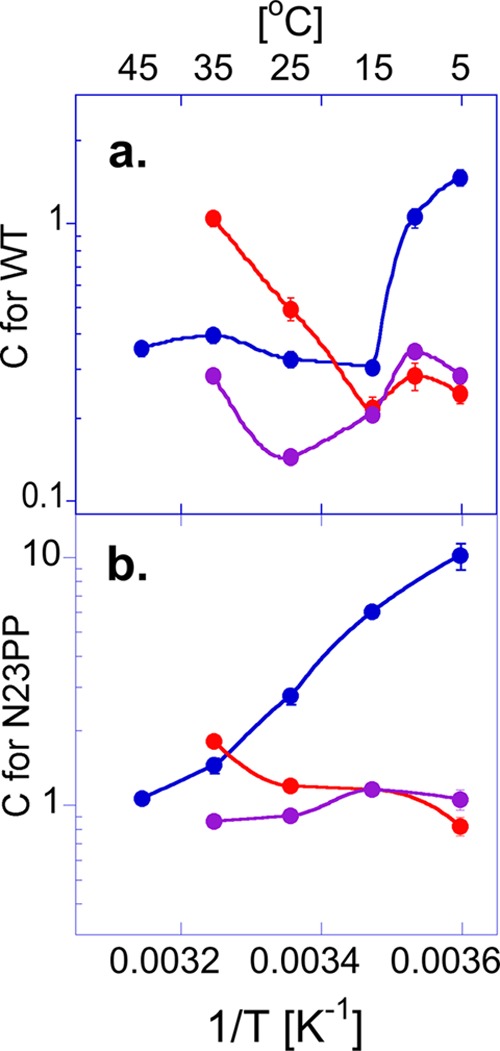
Arrhenius plots of commitments (Cf) for H-transfer. a, Cf for WT ecDHFR determined for the kcat/Km KIEs at pH 9 (blue circles) (14) and observed kH KIEs at pH 7 (red circles) (8) and at pH 9 (purple circles) (8). b, Cf for N23PP (same color codes). The Cf values are presented as average values with S.D. as calculated from Equation 5. The lines are an interpolation of the data and do not represent any fitting (from Ref. 24, with permission from the National Academy of Science).
Kinetic Complexities in WT, N23PP, and N23PP/G51PEKN ecDHFRs
The intrinsic KIEs for N23PP differ from the observed values measured for both second-order rate constants (kcat/Km) at pH 9.0 and pre-steady-state rates (kH) at pH 7.0 (3, 8). Because the intrinsic KIEs of ecDHFR do not vary much with pH and are temperature-independent at both pH 7.0 and 9.0 (Table 1), the explanation for the differences between the observed KIEs measured under steady-state conditions (for kcat/Km) as reported here, and under single turnover conditions (for kH) as reported in Ref. 8 for both the WT and N23PP mutant lies in their kinetic complexities (Cf in Equation 5). Fig. 5 shows the commitments (Cf) for these observed KIEs across the experimental temperature range. Although Cf has a non-linear temperature dependence in WT ecDHFR, a linear trend is observed in the case of N23PP. Also, Cf for kcat/Km is always larger than Cf for kH, due to the observed KIE on kcat/Km involving more microscopic rate constants than the observed KIEs for kH. As reported previously (19) and shown in Fig. 5, the chemical step is less rate-limiting at pH 7.0, resulting in larger Cf at that pH than at pH 9.0. Most importantly, the difference in the temperature dependences of the Cf for kH for the WT versus the N23PP mutant can explain the similarity in the observed KIEs for these enzymes as reported in Ref. 8. The Cf values for kH at pH 7.0 for N23PP are not only larger than for the WTs but are also temperature-dependent, which masks the differences between the WT and the N23PP mutant (Fig. 5). Consistent with the similarities between the intrinsic KIEs of the WT and N23PP/G51PEKN, the Cf values for KIEs on kcat/Km exhibit a similar trend of temperature dependence for the two enzymes. The results presented in Fig. 5 demonstrate that while single turnover measurements better expose the chemical step as compared with steady-state rates, kinetic complexity can still mask the observed KIE from its intrinsic value. These intrinsic values are assessed here by measuring all three isotopes of hydrogen (H, D, and T) and using the Northrop method as done and validated in Refs. 12–14 and 43.
FIGURE 5.
A representative segment of phylogenetically aligned DHFR sequences from human DHFR (hsDHFR) to ecDHFR (24). The phylogenetic tree (not to scale) on the left side illustrates the diverging relationship between species. The values at each divergence node represent the time of divergence for each evolutionary split in units of million of years ago. The human DHFR (hsDHFR) and ecDHFR residue numberings are at the top and bottom of the figure, respectively. homSap, Homo sapiens; macMu1, Macaca mulatta; calJac, Callithrix jacchus; musMus, Mus musculus; canFam, Canis familiarus; loxAfr, Loxodonta africana; monDom, Monodelphis domestica; ornAna, Ornithorhynchus anatinus; galGal, Gallus gallus; xenTro, Xenopus tropicalis; latCha, Latimeria chalumnae; lepOcu, Lepisosteus oculatus; gasAcu, Gasterosteus aculeatus; leuEri, Leucoraja erinacea; eptBur, Eptatretus burgeri; cioInt, Ciona intestinalis; braFlo, Branchiostoma floridae; sacKow, Saccoglossus kowalevskii; strPur, Strongylocentrotus purpuratus; escCol, Escherichia coli.
DISCUSSION
The goal of this study is to relate the role of protein dynamics in the catalyzed C-H→C transfer step in DHFR to the evolution of the enzyme. The effect of protein dynamics on the chemical step of the reaction has been studied through the examination of the temperature dependence of KIEs, as used previously for ecDHFR (8, 9, 12–14) and many other enzymes (25–29). Examination of the intrinsic KIEs for the WT, N23PP, and N23PP/G51PEKN ecDHFR gives insight to the effect that the dynamically altered mutants (3, 24) have on the catalyzed C-H→C transfer. In the framework of Marcus-like models (25–29, 36), the absence of a temperature-dependent KIE is caused by a well defined active site dynamics leading to a narrow distribution of DADs at the TRS. The presence of a temperature-dependent KIE implies a poorly reorganized TRS with broad distribution of DADs. WT ecDHFR exhibits temperature-independent intrinsic KIEs (12), which is consistent with a narrow and well defined DAD distribution at the TRS. The larger and more temperature-dependent KIE of the dynamically rigidified N23PP ecDHFR, however, indicate poorer reorganization of the TRS. This would mean that for the single mutant heavy atom motions do not properly reorganize the active site to achieve the optimal TRS in the WT. As a consequence, at elevated temperatures thermally activated DAD fluctuations populate shorter DADs, from which D can also tunnel, leading to deflation of intrinsic KIEs with increasing temperature (35–36). At low temperature, these fluctuations do not sufficiently populate short DAD from which Asp can tunnel, which leads to larger intrinsic KIE. The temperature independence of the intrinsic KIEs of the N23PP/G51PEKN mutant indicates that the restored dynamics provided by PEKN not only alleviates the reduction in rates observed for the N23PP mutant (24) but also restores the narrow DAD distribution at the TRS of the WT. This finding agrees with the thermally averaged Cα-Cα distance changes computed from the reactant state to the transition state for all pairs of residues in WT, N23PP, and N23PP/G51PEKN DHFRs (Fig. 3) (24). Those calculations suggested that relative to the WT and the double mutant in N23PP many residues across the protein exhibit a much broader spatial distribution along the reaction coordinate for the C-H→C transfer step.
Interestingly, although the NMR relaxation experiments for N23PP ecDHFR (3) suggest rigidification of the protein at the millisecond time scale relative to the WT, the intrinsic KIEs reported here and the dynamics presented in Fig. 3 (24) suggested a broader distribution of DADs at the TRS. This finding is consistent with the concept that the dynamics affecting the TRS formation and DAD distribution are at a much faster timescale than the millisecond time scale examined for the N23PP ecDHFR mutant (3). The elevated millisecond rigidity might reflect the slower kH rate for the mutant, and appears to lead to a poorly reorganized TRS relative to both the WT and the double mutant. The impaired millisecond motions in N23PP brings the system to a non-ideal TRS, where the average DAD is too long for efficient H-tunneling, resulting in larger intrinsic KIEs than for the WT. Thermally activated fluctuations of the DAD lead to a larger population of shorter DADs at higher temperature, resulting in more temperature-dependent KIEs than for the WT.
Comparisons of the commitments observed with the WT and N23PP reveal information regarding the effect of mutation on function. In WT ecDHFR, Cf has two phases at high and low temperatures; however, a linear trend is observed in the case of N23PP, which suggests that a single step is probably responsible for most of the commitment. From the kinetic prospective, that step has to be an isotopically insensitive backward step (48). Because the addition of the biproline sequence at the end of the Met-20 loop restricts its millisecond motion (3), the opening of the Met-20 loop and flipping out of the nicotinamide ring of NADPH from the active site could be slower at lower temperatures (a consequence of the higher Ea for these millisecond conformational fluctuations (3)), contributing significantly to the commitment on KIEs measured for kH.
CONCLUSIONS
From the perspective of the chemical step (C-H→C transfer), the current findings can be rationalized as a disturbance in the WT well reorganized TRS, which is induced by the dynamically altered N23PP mutant (3, 24). Interestingly, along the evolution from bacteria to human this disturbance seems to be prevented in natural DHFRs by the insertion of G51PEKN. Examination of Fig. 5 indicates that the N23PP mutation that altered the enzyme dynamics and is the focus of a heated debate (2, 3, 8) was only introduced in DHFR 325 million years ago (chicken, galGal), well after the “remedying” G51PEKN mutation was introduced 463 million years ago (skate, leuEri). Similarly, G51PEKN was introduced 797 million years ago (hedgehog, strPur), but the first insertion at Asn-23 was only 499 million years ago (hagfish, eptBur). These observations suggest that the controversial Asn-23 insertion was only introduced in species that already had the Gly-51 insertion. In short, the N23PP insertion never compromised the dynamics of the enzyme and the catalyzed H-transfer, as it only evolved after the Gly-51 modification.
Calculations with both WT ecDHFR and the humanized double mutant N23PP/G51PEKN presented more restricted dynamics along the reaction coordinate (from ground state to transition state) than the N23PP (24). As discussed above, this is consistent with the interpretation of the temperature dependence of the intrinsic KIEs (Fig. 4). This correlation between the protein dymanics of ecDHFR variants and their DAD distributions (associated with the temperature dependence of KIEs) implies a role of fast protein motions in enzymatic reactions. Although these motions may not be the dominant factor in enzymatic catalysis (acceleration by many orders of magnitude) (2, 23), they seem to play a critical role in tuning the reaction coordinate toward efficient H-tunneling. Even if tunneling from the TRS only contributes ∼2 kcal/mol to lowering the activation barrier (23), this translates to a factor of ca. 30 in rate acceleration, which can be critical to organism survival, and competitiveness under evolutionary pressure. Because most WT enzymes with their natural substrate and under physiological conditions were found to have temperature-independent KIEs (27), evolutionary pressure seems to preserve the protein dynamics and a narrow DAD distribution at the TRS of many native enzymes. Given DHFR evolution, in which N23PP is always accompanied by G51PEKN (24), it is apparent that evolutionary pressure maintained the native dynamics and narrow DAD distribution at the TRS as DHFR evolved from bacterial toward human enzyme.
Acknowledgments
We thank Stephan Benkovic and Sharon Hammes-Schiffer for fruitful discussions and for providing Ref. 24 before press.
This work was supported by the National Science Foundation (CHE 1149023) and National Institutes of Health (R01 GM65368).
- ecDHFR
- Escherichia coli dihydrofolate reductase
- KIE
- kinetic isotope effects
- DAD
- donor and acceptor distance
- TRS
- tunneling ready state.
REFERENCES
- 1. Boehr D. D., Dyson H. J., Wright P. E. (2006) An NMR Perspective on Enzyme Dynamics. Chem. Rev. 106, 3055–3079 [DOI] [PubMed] [Google Scholar]
- 2. Adamczyk A. J., Cao J., Kamerlin S. C., Warshel A. (2011) Catalysis by dihydrofolate reductase and other enzymes arises from electrostatic preorganization, not conformational motions. Proc. Natl. Acad. Sci. U.S.A. 108, 14115–14120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Bhabha G., Lee J., Ekiert D. C., Gam J., Wilson I. A., Dyson H. J., Benkovic S. J., Wright P. E. (2011) A dynamic knockout reveals that conformational fluctuations influence the chemical step of enzyme catalysis. Science 332, 234–238 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Boekelheide N., Salomón-Ferrer R., Miller T. F., 3rd. (2011) Dynamics and dissipation in enzyme catalysis. Proc. Natl. Acad. Sci. U.S.A. 108, 16159–16163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Dametto M., Antoniou D., Schwartz S. D. (2012) Barrier Crossing in Dihydrofolate Reductase does not involve a rate-promoting vibration. Mol. Phys. 110, 531–536 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Fan Y., Cembran A., Ma S., Gao J. (2013) Connecting Protein Conformational Dynamics with Catalytic Function As Illustrated in Dihydrofolate Reductase. Biochemistry 52, 2036–2049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Liu H., Warshel A. (2007) Origin of the temperature dependence of isotope effects in enzymatic reactions: the case of dihydrofolate reductase. J. Phys. Chem. B 111, 7852–7861 [DOI] [PubMed] [Google Scholar]
- 8. Loveridge E. J., Behiry E. M., Guo J., Allemann R. K. (2012) Evidence that a “dynamic knockout” in Escherichia coli dihydrofolate reductase does not affect the chemical step of catalysis. Nat. Chem. 4, 292–297 [DOI] [PubMed] [Google Scholar]
- 9. Maglia G., Allemann R. K. (2003) Evidence for environmentally coupled hydrogen tunneling during dihydrofolate reductase catalysis. J. Am. Chem. Soc. 125, 13372–13373 [DOI] [PubMed] [Google Scholar]
- 10. Pu J., Ma S., Garcia-Viloca M., Gao J., Truhlar D. G., Kohen A. (2005) Nonperfect synchronization of reaction center rehybridization in the transition state of the hydride transfer catalyzed by dihydrofolate reductase. J. Am. Chem. Soc. 127, 14879–14886 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Radkiewicz J. L., Brooks C. L. (2000) Protein Dynamics in Enzymatic Catalysis: Exploration of Dihydrofolate Reductase. J. Am. Chem. Soc. 122, 255–261 [Google Scholar]
- 12. Sikorski R. S., Wang L., Markham K. A., Rajagopalan P. T., Benkovic S. J., Kohen A. (2004) Tunneling and coupled motion in the Escherichia coli dihydrofolate reductase catalysis. J. Am. Chem. Soc. 126, 4778–4779 [DOI] [PubMed] [Google Scholar]
- 13. Stojković V., Perissinotti L. L., Willmer D., Benkovic S. J., Kohen A. (2012) Effects of the donor-acceptor distance and dynamics on hydride tunneling in the dihydrofolate reductase catalyzed reaction. J. Am. Chem. Soc. 134, 1738–1745 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Wang L., Goodey N. M., Benkovic S. J., Kohen A. (2006) Coordinated effects of distal mutations on environmentally coupled tunneling in dihydrofolate reductase. Proc. Natl. Acad. Sci. U.S.A. 103, 15753–15758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Wong K. F., Selzer T., Benkovic S. J., Hammes-Schiffer S. (2005) Chemical theory and computation special feature: impact of distal mutations on the network of coupled motions correlated to hydride transfer in dihydrofolate reductase. Proc. Natl. Acad. Sci. U.S.A. 102, 6807–6812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Sawaya M. R., Kraut J. (1997) Loop and subdomain movements in the mechanism of Escherichia coli dihydrofolate reductase: crystallographic evidence. Biochemistry 36, 586–603 [DOI] [PubMed] [Google Scholar]
- 17. Boehr D. D., McElheny D., Dyson H. J., Wright P. E. (2006) The dynamic energy landscape of dihydrofolate reductase catalysis. Science 313, 1638–1642 [DOI] [PubMed] [Google Scholar]
- 18. Venkitakrishnan R. P., Zaborowski E., McElheny D., Benkovic S. J., Dyson H. J., Wright P. E. (2004) Conformational changes in the active site loops of dihydrofolate reductase during the catalytic cycle. Biochemistry 43, 16046–16055 [DOI] [PubMed] [Google Scholar]
- 19. Fierke C. A., Johnson K. A., Benkovic S. J. (1987) Construction and evaluation of the kinetic scheme associated with dihydrofolate reductase from Escherichia coli. Biochemistry 26, 4085–4092 [DOI] [PubMed] [Google Scholar]
- 20. Chen S., Wang L., Fahmi N. E., Benkovic S. J., Hecht S. M. (2012) Two Pyrenylalanines in Dihydrofolate Reductase Form an Excimer Enabling the Study of Protein Dynamics. J. Am. Chem. Soc. 134, 18883–18885 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Miller G. P., Benkovic S. J. (1998) Strength of an interloop hydrogen bond determines the kinetic pathway in catalysis by Escherichia coli dihydrofolate reductase. Biochemistry 37, 6336–6342 [DOI] [PubMed] [Google Scholar]
- 22. Rajagopalan P. T., Lutz S., Benkovic S. J. (2002) Coupling interactions of distal residues enhance dihydrofolate reductase catalysis: mutational effects on hydride transfer rates. Biochemistry 41, 12618–12628 [DOI] [PubMed] [Google Scholar]
- 23. Kamerlin S. C., Warshel A. (2010) At the dawn of the 21st century: Is dynamics the missing link for understanding enzyme catalysis? Proteins 78, 1339–1375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Liu C. T., Hanoian P., French J. B., Pringle T. H., Hammes-Schiffer S., Benkovic S. J. (2013) Functional significance of evolving protein sequence in dihydrofolate reductase from bacteria to humans. Proc. Natl. Acad. Sci. U.S.A. 110, 10159–10164 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Hay S., Scrutton N. S. (2012) Good vibrations in enzyme-catalysed reactions. Nat. Chem. 4, 161–168 [DOI] [PubMed] [Google Scholar]
- 26. Kanaan N., Ferrer S., Martí S., Garcia-Viloca M., Kohen A., Moliner V. (2011) Temperature dependence of the kinetic isotope effects in thymidylate synthase. A theoretical study. J. Am. Chem. Soc. 133, 6692–6702 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Nagel Z. D., Klinman J. P. (2010) Update 1 of: Tunneling and dynamics in enzymatic hydride transfer. Chem. Rev. 110, PR41–PR67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Hammes-Schiffer S. (2006) Hydrogen tunneling and protein motion in enzyme reactions. Acc. Chem. Res. 39, 93–100 [DOI] [PubMed] [Google Scholar]
- 29. Wang Z., Abeysinghe T., Finer-Moore J. S., Stroud R. M., Kohen A. (2012) A remote mutation affects the hydride transfer by disrupting concerted protein motions in thymidylate synthase. J. Am. Chem. Soc. 134, 17722–17730 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Markham K. A., Sikorski R. S., Kohen A. (2003) Purification, analysis, and preservation of reduced nicotinamide adenine dinucleotide 2′-phosphate. Anal. Biochem. 322, 26–32 [DOI] [PubMed] [Google Scholar]
- 31. Antoniou D., Caratzoulas S., Kalyanaraman C., Mincer J. S., Schwartz S. D. (2002) Barrier passage and protein dynamics in enzymatically catalyzed reactions. Eur. J. Biochem. 269, 3103–3112 [DOI] [PubMed] [Google Scholar]
- 32. Roston D., Cheatum C. M., Kohen A. (2012) Hydrogen donor-acceptor fluctuations from kinetic isotope effects: a phenomenological model. Biochemistry 51, 6860–6870 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Sutcliffe M. J., Masgrau L., Roujeinikova A., Johannissen L. O., Hothi P., Basran J., Ranaghan K. E., Mulholland A. J., Leys D., Scrutton N. S. (2006) Hydrogen tunnelling in enzyme-catalysed H-transfer reactions: flavoprotein and quinoprotein systems. Philos. Trans. R. Soc. Lond. B Biol. Sci. 361, 1375–1386 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Wang Z., Roston D., Kohen A. (2012) Experimental and theoretical studies of enzyme-catalyzed hydrogen transfer reactions in Structural and Mechanistic Enzymology: Bringing Together Experiments and Computing (Christov C. Z., Karabencheva T., eds), pp. 155–180, Elsevier, Inc., Oxford, UK: [DOI] [PubMed] [Google Scholar]
- 35. Cheatum C. M., Kohen A. (2013) Relationship between femtosecond-picosecond dynamics to enzyme-catalyzed H-transfer. Top. Curr. Chem. 337, 1–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Klinman J. P., Kohen A. (2013) Hydrogen tunneling links protein dynamics to enzyme catalysis. Ann. Rev. Biochem. 82, 471–496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Kohen A. (2003) Kinetic Isotope Effects as Probes for Hydrogen Tunneling, Coupled Motion and Dynamics Contribution to Enzyme Catalysis. Prog. Reac. Kin. Mech. 28, 119–156 [Google Scholar]
- 38. Kohen A., Limbach H. H. (Eds) (2006) Isotope Effects in Chemistry and Biology, CRC Press, Taylor and Francis, Boca Raton, FL [Google Scholar]
- 39. Glowacki D. R., Harvey J. N., Mulholland A. J. (2012) Taking Ockham's razor to enzyme dynamics and catalysis. Nat. Chem. 4, 169–176 [DOI] [PubMed] [Google Scholar]
- 40. Blakley R. L. (1960) Crystalline dihydropteroylglutamic acid. Nature 188, 231–232 [Google Scholar]
- 41. McCracken J. A., Wang L., Kohen A. (2004) Synthesis of R and S tritiated reduced β-nicotinamide adenine dinucleotide 2′ phosphate. Anal. Biochem. 324, 131–136 [DOI] [PubMed] [Google Scholar]
- 42. Markham K. A., Sikorski R. S., Kohen A. (2004) Synthesis and utility of 14C-labeled nicotinamide cofactors. Anal. Biochem. 325, 62–67 [DOI] [PubMed] [Google Scholar]
- 43. Sen A., Yahashiri A., Kohen A. (2011) Triple isotopic labeling and kinetic isotope effects: exposing H-transfer steps in enzymatic systems. Biochemistry 50, 6462–6468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Melander L., Saunders W. H. (1987) Reaction rates of isotopic molecules, Malabar, FL [Google Scholar]
- 45. Kohen A. (2006) Kinetic isotope effects as probes for hydrogen tunneling in enzyme catalysis in Isotope effects in Chemistry and Biology (Kohen A., Limbach H. H., Eds.), pp. 743–764, Taylor & Francis, CRC Press, Boca Raton, FL [Google Scholar]
- 46. Ferrer S., Silla E., Tuñón I. A., Martí S., Moliner V. (2003) Catalytic Mechanism of Dihydrofolate Reductase Enzyme. A Combined Quantum-Mechanical/Molecular-Mechanical Characterization of the N5 Protonation Step. J. Phys. Chem. B 107, 14036–14041 [Google Scholar]
- 47. Loveridge E. J., Behiry E. M., Swanwick R. S., Allemann R. K. (2009) Different Reaction Mechanisms for Mesophilic and Thermophilic Dihydrofolate Reductases. J. Am. Chem. Soc. 131, 6926–6927 [DOI] [PubMed] [Google Scholar]
- 48. Cook P. F., Cleland W. W. (2007) Enzyme Kinetics and Mechanism, Garland Publishing, Inc., New York, NY [Google Scholar]
- 49. Northrop D. B. (1981) Minimal kinetic mechanism and general equation for deuterium isotope effects on enzymic reactions: uncertainty in detecting a rate-limiting step. Biochemistry 20, 4056–4061 [DOI] [PubMed] [Google Scholar]