Breast density quantification using magnetic resonance imaging (MRI) with bias field correction: A postmortem study

Abstract

Purpose: Quantification of breast density based on three-dimensional breast MRI may provide useful information for the early detection of breast cancer. However, the field inhomogeneity can severely challenge the computerized image segmentation process. In this work, the effect of the bias field in breast density quantification has been investigated with a postmortem study.

Methods: T1-weighted images of 20 pairs of postmortem breasts were acquired on a 1.5 T breast MRI scanner. Two computer-assisted algorithms were used to quantify the volumetric breast density. First, standard fuzzy c-means (FCM) clustering was used on raw images with the bias field present. Then, the coherent local intensity clustering (CLIC) method estimated and corrected the bias field during the iterative tissue segmentation process. Finally, FCM clustering was performed on the bias-field-corrected images produced by CLIC method. The left–right correlation for breasts in the same pair was studied for both segmentation algorithms to evaluate the precision of the tissue classification. Finally, the breast densities measured with the three methods were compared to the gold standard tissue compositions obtained from chemical analysis. The linear correlation coefficient, Pearson's r, was used to evaluate the two image segmentation algorithms and the effect of bias field.

Results: The CLIC method successfully corrected the intensity inhomogeneity induced by the bias field. In left–right comparisons, the CLIC method significantly improved the slope and the correlation coefficient of the linear fitting for the glandular volume estimation. The left–right breast density correlation was also increased from 0.93 to 0.98. When compared with the percent fibroglandular volume (%FGV) from chemical analysis, results after bias field correction from both the CLIC the FCM algorithms showed improved linear correlation. As a result, the Pearson's r increased from 0.86 to 0.92 with the bias field correction.

Conclusions: The investigated CLIC method significantly increased the precision and accuracy of breast density quantification using breast MRI images by effectively correcting the bias field. It is expected that a fully automated computerized algorithm for breast density quantification may have great potential in clinical MRI applications.

INTRODUCTION

Breast density, which is quantified as the volume percentage of glandular tissue over the whole breast volume, has been recognized as an independent risk factor associated with the development of breast cancer. The positive association between a qualitative classification of breast density and breast cancer risk was first suggested by Wolfe.¹ This relationship has been substantially confirmed by more recent studies.^{2, 3, 4} It has been suggested that women with a mammographic breast density higher than 75% have a four- to sixfold higher risk of developing breast cancer than women with little or no dense tissue.² Due to its significance, the Breast Cancer Prevention Collaborative Group (BCPCG) has suggested that models incorporating breast density should be developed to increase the predictive power for an individual's breast cancer risk.⁵ The members of BCPCG also recommended that quantitative estimations, especially using computer-assisted automatic methods, have the advantage over qualitative or semiquantitative classifications, such as the Wolfe or the Breast Imaging-Reporting and Data System (BIRADS),⁶ with respect to objectivity and accuracy, due to its continuous rather than a categorical scale. However, so far, no commonly accepted method exists for quantification of breast density, due to the difficulties in standardization and limitations in accuracy.

Currently, breast imaging techniques that have been approved by U.S. Food and Drug Administration (FDA) to view the internal tissue and detect suspicious lesions in a breast include mammography, digital breast tomosynthesis, and magnetic resonance imaging (MRI). Mammography is the most widely used breast screening tool, owing to its ease of implementation, high spatial resolution, and low cost. Because of this, most breast density estimations are based on areal measurements on mammograms. However, the 2D projection nature of the technique bears the intrinsic limitation of overlapping tissue and ignores the 3D characteristics of a breast. The areal measurements simply dichotomize each pixel as either pure glandular or pure adipose, which cannot provide an accurate measurement of volumetric breast density. In addition, the current mammography technique is designed for breast cancer detection, not for breast density estimation. The imaging protocols are routinely varied according to the compression thickness of the breast to improve the contrast. At the same time, clinical mammograms are usually preprocessed by built-in proprietary software for better visualization of suspicious lesions. The implementation of these techniques leads to great challenges for standardization of breast density estimation methods, particularly for computer-assisted fully automatic algorithms. Digital breast tomosynthesis, which has recently been approved by the FDA, is generally considered as a compromise between 2D projection-based and fully 3D imaging techniques.⁷ Typically, 9–25 low-dose projection images are acquired at different angles around the compressed breast, and then reconstructed to obtain multiple images at different depth of the entire breast volume.^{8, 9} This approach has shown to improve the contrast of the image for better lesion detection by reducing tissue overlap.¹⁰ However, tomosynthesis cannot remove the overlapping tissues completely among different slices due to poor resolution along the depth direction.¹¹ This introduces challenges in breast density quantification. Currently, there is no standard method for breast density estimation for the reconstructed images from digital tomosynthesis. One of the first breast density studies on digital tomosynthesis¹² used only the center projection images, in which case it shares somewhat similar limitations as mammography.

Breast MRI has been recently recommended by the American Cancer Society as an adjunct breast screening tool for high-risk patients.¹³ In contrast to mammography, the 3D information obtained from MRI can potentially be used to accurately quantify glandular volume in a breast. Furthermore, tissue contrast in MRI relies on differences in relaxation rates (T1 or T2) of the glandular and the adipose tissues. Since MRI does not involve any ionizing radiation, the imaging protocols can be easily optimized to improve the image quality without worrying about the dose to the patient. Several studies have reported on the use of MRI for breast density quantification,^{14, 15} most of which used T1-weighted imaging protocols. This allows for easy implementation of computer-assisted algorithms for threshold-based segmentation of glandular and adipose tissue. Unlike mammography, MRI produces hundreds of slices for each breast pair. Therefore, it is critical to develop a fully automated algorithm for breast density quantification. The main difficulty in MRI segmentation is the intensity inhomogeneity, which is usually referred to as the “bias field.” Studies have suggested that the bias field can result in intensity variations as much as 30%, which may lead to significant errors in breast density quantification.¹⁶

Bias field is usually introduced by inevitable imperfections in the radio frequency (RF) coil, by gradient-driven eddy currents, and by the patients’ anatomy.¹⁷ After inverse Fourier transformation, the bias field often presents as a slowly varying intensity variation across the image. This artifact, although sometimes ignorable by an experienced human observer, will severely sabotage the accuracy of computer-assisted segmentation methods. Therefore, the bias field has to be estimated and corrected for a reliable measurement of breast density.¹⁸ In general, bias field can be corrected both prospectively, through system calibration, and retrospectively with computer-based image processing algorithms. Prospective methods can be used to correct the bias field associated with the MRI hardware. However, inhomogeneity induced by patient positioning and anatomy can only be corrected using retrospective methods. MRI algorithms and methods specific to breast imaging are currently being explored in the literature in an effort to produce completely quantitative measures of breast density. A commonly used algorithm for bias field estimation is the expectation maximization (EM) method.^{19, 20} Wells et al. proposed an adaptive statistical approach based on the EM algorithm, which combines the task of bias field correction and tissue classification during the interleaved iterative process.¹⁹ The major problem with the EM algorithm is that it requires a priori knowledge of the tissue structure. A poor choice of the initial values may result in an incorrect estimation of both bias field and tissue classification, due to the fact that the iterative process may be trapped to a local minimum. A nonparametric nonuniform intensity normalization (N3) algorithm has been proposed by Sled et al. in 1998.²¹ N3 algorithm uses a Gaussian model for the bias field and does not require a priori tissue segmentation information. This technique, as well as its variation N4 algorithm,²² which has an improved B-spline fitting routine, can be implemented for fully automatic image processing and are widely used methods. However, the N3 algorithm was originally developed for brain images where the field inhomogeneity is generally less due to small field of view in comparison to breast imaging. A recent study has suggested that using N3 algorithm alone may not be sufficient for bias field correction of breast images.¹⁸ Recently, a new energy minimization method using coherent local intensity clustering (CLIC) was introduced by Li et al. based on the fuzzy c-means (FCM) algorithm.²³ CLIC method is robust to initialization and is capable of generating a smooth bias field due to the coherent nature of the criterion function. Both the bias field estimation and tissue classification can be calculated simultaneously with the CLIC method, which allows for fully automatic computer-assisted applications.

The CLIC method has been successfully applied in MRI brain imaging to segment white matter, gray matter, and cerebral spinal fluid (CSF).^{23, 24} There are only few studies on breast density quantifications using the CLIC method on MRI images.¹⁸ One major limitation for a clinical MRI segmentation study is the lack of a gold standard for breast density estimation. Since there is no grand truth in this case, the accuracy of the segmentation methods cannot be evaluated quantitatively. The qualitative assessment by radiologists introduces unavoidable inter- and intraobserver variability in the study results. In the present study, we investigate the bias field effect on MRI breast density quantification by comparing the standard FCM algorithm and the CLIC method on 40 postmortem breasts. After imaging, samples were chemically decomposed into water, lipid, and protein contents. This definitive measurement of the chemical composition of the postmortem breasts was used as the gold standard.²⁵ The linear correlation between the breast density obtained from MRI and the result from chemical analysis was studied for both methods.

METHODS

Subjects

Twenty pairs (left and right) of postmortem breasts were acquired from the Willed Body Program in the School of Medicine at the University of California, Irvine. The right and left breasts were surgically removed from the cadaver to the pectoralis major muscle. They were carefully labeled and frozen inside plastic bags. The mass of the breast samples varied from 136 to 2330 g. The breast densities also varied in a large range, according to our chemical analysis. The breast samples were removed from the freezer and kept at approximately 4 °C for a day before the experiment. To prevent any water loss during the experiment, each sample was packed in a plastic bag during the scan. Before each scan, samples were kept at room temperature for at least 20 min to allow for tissue relaxation.

Breast MRI was carried out on an Aurora 1.5 Tesla dedicated breast MRI scanner (Aurora Imaging Technology, Inc., North Adnover, MA). The left and right breasts from the same pair were scanned together using the FLASH sequence to generate a set of 3D T1-weighted images without fat saturation. The repetition time (TR) and the echo time (TE) were set at 11 and 4.7 ms. The flip angle was 20°. The field of view (FOV) was set to 30 cm with a matrix size of 320 × 320 and a slice thickness of 2 mm for all samples. The total imaging time for each postmortem breast pair was approximately 2.5 min.

Bias field correction and tissue classification

Generally, segmentation algorithms split a collection of objects into a number of distinct groups based on some measure of distance between the objects. Such algorithms are used in diverse fields such as image analysis, pattern recognition, data mining, and computer vision. For the specific case of analyzing images of biological tissues, the algorithm separates the pixels by gray value into a number of nonoverlapping regions. K-means clustering is a fundamental clustering algorithm. In mathematical terms, the goal is to separate a set of N pixels, p_i, into k classes, denoted by {S₁, S₂, …, S_k} with unique cluster centers (c₁, c₂, …, c_k) in order to minimize the sum of squares within cluster:

$$\begin{array}{c}\hfill {}_S{}^{\arg \min }\sum _{i=1}^k{\sum }_{pj\in S_i}{\left|p_j-c_i\right|}^2\mathrm{where}{c}_i=\frac{1}{\left|S_i\right|}{\sum }_{pj\in S_i}{p}_j.\end{array}$$ (1)

The FCM algorithm generalizes this “hard” segmentation to fuzzy logic by allowing each pixel to belong to each of the classes. Instead of partitioning into sets, fuzzy c-means calculates a membership matrix U s.t. $\forall i{\sum }_{j=1}^k{u}_{ij}=1$. This fuzzy classification improves the robustness of the algorithm, producing segmentations that are more accurate.²⁶

However, FCM algorithm is generally not sufficient to perform the bias field correction on images. In this study, the CLIC method was used to evaluate and correct the bias field as well as quantify glandular volumes in the images. CLIC is a FCM-based algorithm that combines the processes of bias field correction and segmentation into a single iterative process. The method assumes that the bias field is a multiplicative factor that varies slowly across the image volume and is therefore approximately piecewise constant. Then the measured signal in each voxel, I(x), is given by¹⁶

$$I\left(x\right)=b\left(x\right)\times j\left(x\right)+n\left(x\right),$$ (2)

where b is the bias field, J is the true signal from the tissue, and n is additive zero-mean Gaussian noise. Then the goal is to estimate b and J simultaneously. This is done by considering small spherical neighborhoods of radius ρ for each pixel x within which the bias field can be estimated as a constant, i.e., as b(x). Then we can segment the local region using a FCM algorithm where the cluster centers under the bias field are given by b(x)c_i. Also, we would want the weight of intensities I(y) far from the cluster center x to have less influence on the clustering. The goal of minimizing the global energy is reached by minimizing the local energy in each of the small regions, or equivalently, minimizing the integral of the local function over the whole volume. Note that by the definition of the weighting kernel, pixels outside of the region of interest contribute nothing. This leads us to defining the global energy function as

$$\begin{array}{ccc}& & {\mathcal{J}}_x\left(U,\mathit{c},b\left(x\right)\right)\hfill \\ & & =\int {\sum }_{i=1}^k\int u_i^q\left(y\right)K(x-y){\left|I\left(y\right)-b\left(x\right)c_i\right|}^{2}dydx,\hfill \end{array}$$ (3)

where K(x − y) is the weight assigned to the intensity I(y) and is chosen to be a truncated Gaussian kernel and q is called the fuzzifier, which relates to the “fuzziness,” or spread in the distribution, of the segmentation.

The minimization of the above function, which is convex in each of its variables, is then carried out in an iterative process of minimization with respect to the variables U, c, and b separately. The best estimates for each of these variables at each iteration are given by the following three equations:

$${\widehat{C}}_i=\frac{\int (b*K)I{u}_i^{q}dx}{\int (b^2*K)I{u}_i^{q}dx},i=1,...,k,$$ (4)

$$\widehat{b}=\frac{\left(I{\sum }_{i=1}^k{c}_i{u}_i^q\right)*K}{I{\sum }_{i=1}^k{c}_i^2{u}_i^q*K},$$ (5)

$${\widehat{u}}_i^q\left(y\right)=\frac{1}{{\sum }_{j=1}^k{\left(\frac{d_i\left(I\left(y\right)\right)}{d_j\left(I\left(y\right)\right)}\right)}^{\frac{1}{q-1}}}.$$ (6)

More details of the CLIC method can be found in the report by Li et al.²³

To evaluate the effect of bias field, we compared the breast segmentation results from three studies: (a) FCM clustering on raw images; (b) CLIC clustering on raw images; and (c) FCM clustering on bias-field-corrected images. In study (a), Basic FCM algorithm was applied to the raw MRI images of the postmortem breast samples. Six clusters were used for the image segmentation based on previous segmentation studies of breast images.^{15, 18} Other cluster numbers were also tested. However, less than six clusters were generally insufficient for successful segmentation as determined by visual assessment. Increasing the number of clusters above six showed only minimal improvement in tissue segmentation. After the clustered images were generated by the FCM algorithm, a physicist, who has two years of training in clinical image processing, reviewed the entire image data set for glandular segmentation. One or more clusters were assigned as glandular tissue with visual assessment by comparing the clustered and raw images. The segmentation and visual assessment were accomplished with ImageJ, an open source scientific image processing program.²⁷

In the second study, the CLIC method was applied on the raw images to correct the effects of the bias field and segment the 3D images into two tissues (k = 2), glandular and adipose. The fuzzifier, q, was also set to 2 for this algorithm. In order to accurately segment the images using two clusters, the background was first removed from the calculations. Since only postmortem breasts without any other anatomical structures were imaged, the background of the images was homogenous. In the nonfat saturated MRI images, the breast tissue generally has high voxel values with significant contrast with respect to the background. Therefore, removing the background was relatively easy in this study. In principle, this can be done by standard histogram thresholding method using a single threshold. However, in order to implement a fully automatic segmentation process, we performed an automatic five-cluster FCM on the entire volume image and then selected the lowest cluster as the background. The voxels that were assigned as background were excluded in the following CLIC segmentation. For CLIC segmentation, the local regions were chosen to be spheres with a radius of 7 mm, and the standard deviation of the Gaussian kernel, K, was set to 3.5 mm. After running the algorithm, the voxels that were selected as glandular and adipose tissue were counted and converted into volumes. Then, the breast densities were derived as the ratio of the glandular volume over the total breast volume. Both FCM and CLIC methods have implemented edge removal functions, which can exclude skin during breast tissue segmentation. However, the skin removal function was not used in this study. This is mostly because of the fact that skin was also included during tissue chemical decomposition. Although skin is different from glandular tissue, its chemical compositions and imaging properties are quite similar to those of glandular tissue. To have a direct comparison between image-based breast density measurement and %FGV from chemical analysis, the contribution of skin was included for both FCM and CLIC methods.

The CLIC algorithm performed bias field correction and tissue segmentation simultaneously in an iterative process. Besides the clustered images, bias-field-corrected images were also obtained from the raw image. The basic FCM algorithm was used before and after bias field correction to evaluate the benefit of bias field correction in breast tissue segmentation. In the clustered images, the histogram separation of each cluster was generally large, so the bias induced by human observers can be substantially reduced. To evaluate the potential subjective variation in the semiautomatic FCM segmentation method, two physicists were asked to segment the glandular tissue from the clustered images independently. A two-hour training session was scheduled for both readers at the same time. Eight samples, which varied in size and breast density, were selected for the training session. After the training session, the two readers performed the glandular segmentation independently.

Chemical analysis

In order to have a gold standard for the tissue compositional analysis, all postmortem breasts, including skin, were chemically decomposed into their water, lipid, and protein contents after the MRI scans. The chemical analysis method was based on a standardized procedure devised by the United States Department of Agriculture to measure the amount of water, lipid, protein and minerals in a sample.²⁸

Each postmortem breast was weighed before and after the MRI scan. The change in sample mass was assigned to water loss, and added into the final water fraction. After imaging, each sample was cut into small cubical pieces of approximately 5 × 5 × 5 mm³ and placed into a vacuum oven maintained at approximately 95 °C for 48 h to evaporate all remaining water. The sample was removed from the vacuum and weighed once again. The mass lost during baking was assumed to be purely water. The dried sample was then mixed with petroleum ether, ground into a slurry, and agitated at 30 °C for approximately 1 h to dissolve the lipid contents of the fatty tissue into the ether solvent. The sample was then cooled at room temperature (approximately 20 °C) for 24 h. Next, the ether solution was vacuum filtered through a Buchner funnel. One additional liter of pure petroleum ether was passed over the sample to wash away any residual lipid contents. Therefore, the petroleum ether solution was assumed to contain the entire lipid from the sample. The lipid material was then isolated from the solution by evaporating the petroleum ether under vacuum distillation. The isolated lipid was weighed, yielding the lipid mass. The dried material remaining in the filter after filtration contained mostly protein with a very small amount of minerals, such as Na, K, and Ca. To separate the pure protein mass, we followed an “ashing” procedure adapted from the Handbook of Food Analysis.²⁹ Each sample was placed in a crucible and baked in a furnace with excess air at 550 °C for 18 h, so that all carbon-based compounds were oxidized and removed from the ash. The difference in weight before and after the high temperature baking was assigned to pure protein mass. Further analysis was performed on the remaining ash to determine the amount of Ca in the tissue by removing the water soluble components. Finally, the measured masses of water, lipid, and protein were converted into volumes, and the volumetric fractions of the three materials were used as the gold standard for the evaluation of breast density.

Statistical analysis

In the current study, the definitive measurements of the chemical decomposition of the postmortem breast samples were used as the gold standard for breast density estimation. However, water, lipid, and protein are common to both glandular and adipose tissues with different concentrations. In order to relate breast density from MRI image segmentation and compartment measurement from chemical analysis, the percent fibroglandular volume (%FGV) has previously been proposed as a tissue compositional metric, which is defined as the volumetric ratio of water and protein to the total volume.³⁰ The relation between breast density and %FGV can be analytically derived, assuming that the chemical composition, in terms of the volumetric fractions of water (W), lipid (L), and protein (P) contents, of either pure glandular (G), or pure adipose tissue (A) varies in a small range.³¹ The total fraction of each component can then be represented by the following three equations:

$$X=X_G*G+X_A*A\mathrm{for}X\in \{W,L,P\}.$$ (7)

Knowing that the sum of glandular and adipose tissues is the same as the sum of the water, lipid, and protein contents, one can then find breast density (BD) in terms of %FGV by simple algebra

$$\begin{array}{c}\hfill \mathrm{BD}=\frac{\%\mathrm{FGV}-(W_A+P_A)}{(W_G+P_G)-(W_A+P_A)}=\frac{\%\mathrm{FGV}-{\%\mathrm{FGV}}_A}{\%{\mathrm{FGV}}_G-{\%\mathrm{FGV}}_A},\end{array}$$ (8)

where %FGV_A and %FGV_G represent the fibroglandular ratios of pure adipose and pure glandular tissue, respectively. Equation. 8 can be easily justified through two extreme cases: (1) when the breast is completely glandular, i.e., %FGV = %FGV_G, breast density becomes 1; (2) when it is completely adipose, i.e., %FGV = %FGV_A, breast density becomes 0. It is clear that the relation between breast density and %FGV has the form of a simple linear function with a slope and an intercept that are related to the chemical composition of pure glandular and pure adipose tissues. More detailed discussion about this relationship has been reported in another study.³²

Two sets of statistical analysis were performed in this study. First, the precision of the investigated image segmentation and bias field correction methods was evaluated by linear regression of the breast densities measured from the left and right breasts of the same pair. Then, the accuracy of the two methods was further studied through the linear correlation between the measured breast density and the %FGV. In both cases, Pearson's r obtained from the linear regression was used to evaluate the effect of bias field on segmentation in breast MRI. Standard error of the estimate (SEE) was also used in the breast density and %FGV comparisons for different algorithms.

RESULTS

We first investigated the left-right correlation of breasts from the same donor using the standard FCM method without bias field correction and the CLIC method which simultaneously corrected the bias field and segmented the image. The left–right correlations of the glandular volume and the breast density as measured with FCM method are presented in Figs. 1a, 1b, respectively. Linear fittings of the measured data are shown as the straight lines in both figures. The slopes derived from the linear fittings were approximately 0.71 and 1.03 for the glandular volume and breast density correlation, respectively. Pearson's r derived from volume correlation analysis was estimated to be 0.70. A much better linear correlation was found when comparing the breast density data, where the Pearson's r was found to be 0.93. The left–right correlations obtained with the CLIC method are shown in Figs. 2a, 2b for the glandular volume and breast density, respectively. Similar statistical analysis was performed in this case, where the slopes derived from linear fittings were estimated to be 0.94 and 1.02 for the glandular volume and breast density, respectively. It should also be noted that the intercept in breast density fitting was almost negligible. Furthermore, Pearson's r was significantly improved when the effects of the bias field were corrected in the segmentation process. This is particularly true for glandular volume estimations. The left–right correlation obtained from the FCM segmentation on the bias-field-corrected images was very similar to that from the CLIC method. The linear correlation coefficient was estimated to be 0.96 for breast density comparison, which corroborates the above conclusion that the precision of the image segmentation techniques can be improved by correcting the bias field.

Figure 1.

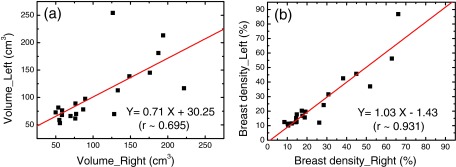
Left–right comparison between breasts from the same pair for the glandular volume (a) and breast density (b) measured with the standard FCM method, where the effect of bias field has not been corrected in the raw images. The linear fittings are shown as the straight lines in the plots. The fitting parameters and the correlation coefficients are shown for both plots.

Figure 2.

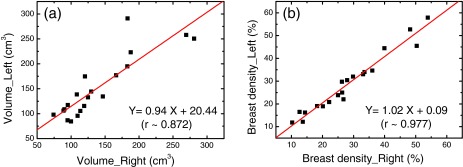
Left–right comparison between breasts from the same pair for the glandular volume (a) and breast density (b) measured with the CLIC method, which estimated and corrected the bias field during tissue segmentation. The linear fittings are shown as straight lines in the plots. The fitting parameters and the correlation coefficients are shown for both plots.

In order to quantify breast density in a set of 3D images of a breast, one needs to estimate two volumes. Besides the assessment of glandular volume, it is also necessary to accurately separate the breast from the background so that the total volume of the breast can be calculated. In a postmortem study, this step is relatively easy due to the absence of the surrounding anatomy and the high contrast between breast tissue and air background in nonfat-saturated images. Nevertheless, the total volume estimation remains a good way to assess the consistency and accuracy of the image segmentation algorithms used in this study. The estimated total breast volume is plotted as a function of that derived from chemical analysis in Figs. 3a, 3b for the FCM and the CLIC methods, respectively. To get the breast volumes from the image-based analysis, the homogenous background of the image was removed by rejecting the cluster with the lowest pixel values. Then the total number of tissue voxels was obtained by summing all the remaining clusters together. Finally, the size of the voxel determined by the imaging protocols was used to convert the total number of voxels into a volume measurement. Total volumes from the chemical analysis were calculated from the definitive mass measurements of water, lipid, and protein contents with the corresponding mass density values. Although breast tissue can also contain minerals, such as Ca, their contribution to the total volume is so small that they can be safely ignored. For both segmentation methods, the linear fittings in Fig. 3 gave a slope of 1 and negligible intercept with r > 0.99. The results indicate that both methods can accurately measure the total breast volume, suggesting that the bias field has minimal effect in total volume assessment of the postmortem breast samples.

Figure 3.

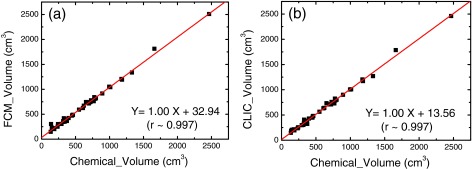
Total breast volumes measured with the FCM (a) and CLIC (b) methods as a function of that obtained from the chemical analysis. Both methods can successfully predict the breast volume with correlation coefficients over 0.99.

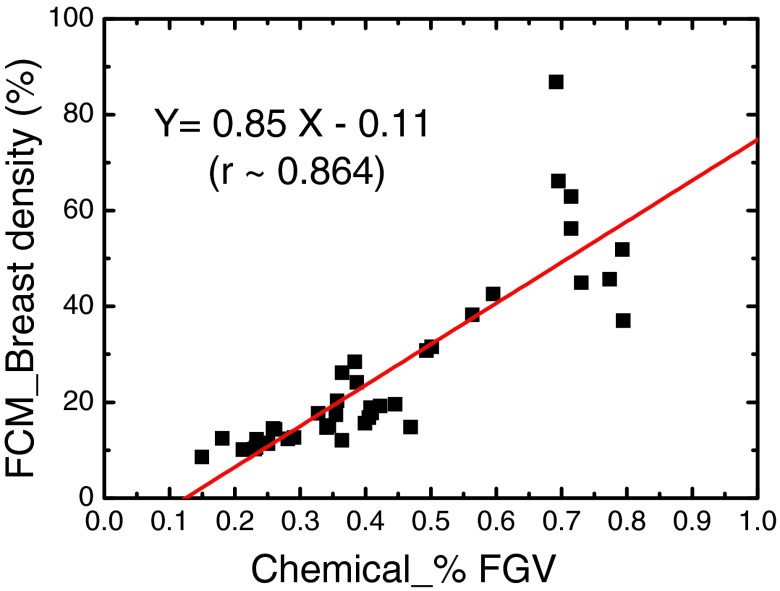
Finally, we compared the breast density measured with the two methods with the %FGV obtained from chemical analysis. As we discussed in Sec. 2D, a linear correlation is expected between the two variables. Since errors in the chemical analysis are expected to be negligible,²⁵ we used %FGV as the gold standard for objective evaluations of the investigated methods and the effects of the bias field correction by comparing the Pearson's r coefficients. In Fig. 4, the breast density estimated by the FCM method on the raw images is plotted as a function of the %FGV obtained from chemical analysis. The linear fitting is shown as the straight line in the plot. A fairly good linear correlation can be found with r equal to 0.86. However, the method seems to fail on some cases, as indicated by the outliers in the plot.

Figure 4.

The correlation between breast densities measured with the FCM method and the %FGV from chemical analysis. The linear fitting is shown as the straight line. The Pearson's r is estimated to be 0.86.

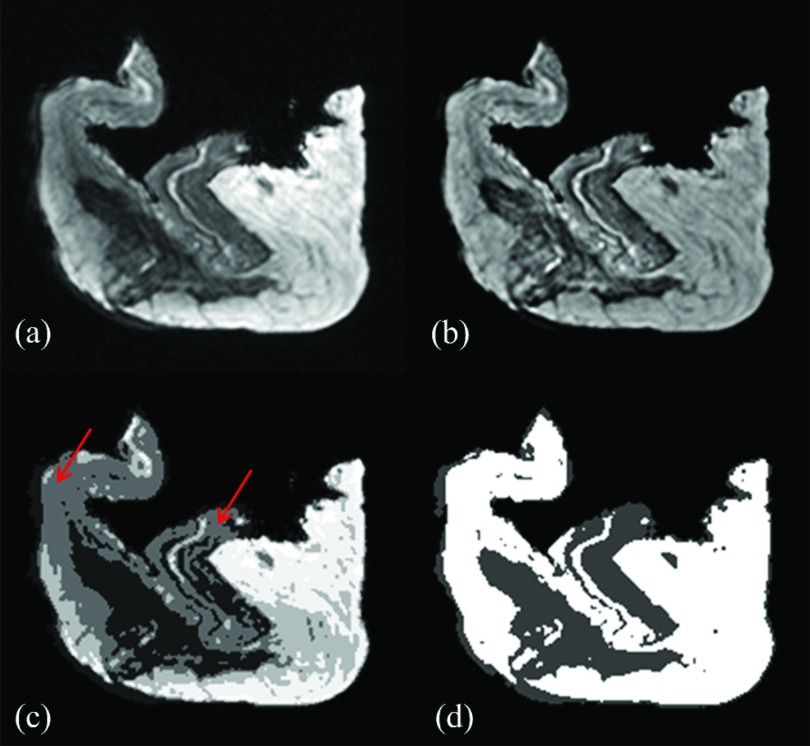
An example of the bias field effect is presented in Fig. 5a, where a representative postmortem breast image is shown in transverse view before any bias field correction. The surgically removed postmortem breast images appear different from the standard breast MRI images. The bright and dark regions of the image represent the adipose and glandular tissues, respectively. Intensity inhomogeneity induced by the bias field can be clearly identified in the adipose region in the upper–left corner, where the adipose tissue was significantly darker than the adipose tissue on the right side of the image. The presence of the bias field in this image severely hampers the application of the computerized image segmentation algorithms, since the narrow Gaussian tissue classification model fails to apply in this case. Figure 5b shows the same image after bias field correction, which corrected the intensity inhomogeneity. The pixel values in the image now truthfully represent the expected intensities of the corresponding tissue. The segmentations of the raw and bias field-corrected images are shown in Figs. 5c, 5d, respectively. Different clusters are shown in gray levels in both images. Due to the presence of the bias field, the standard FCM method on raw images was not able to differentiate the adipose tissue on the top-left and the glandular tissue in the middle of the image, as indicated by the arrows in Fig. 5c. As a result, when selecting the middle glandular tissue during the segmentation process by choosing two clusters, a large volume of adipose tissue will be mistakenly included as well. This led to significant overestimation of the glandular volume. At the same time, using only the lowest cluster resulted in an underestimation of the glandular volume. This contradiction cannot be easily solved with basic FCM algorithm by increasing the number of clusters, since the pixel values in those regions were too close to each other due to the presence of the bias field. On the other hand, the CLIC method, which estimated and corrected the bias field, was able to accurately perform the tissue segmentation, as shown in Fig. 5d. When FCM algorithm was applied to the bias-field-corrected image, a correct segmentation can then be obtained, which appeared very similar to that obtained from the CLIC method. Note that, in both methods, skin was included in the estimation of the glandular volume, so that the results can be directly compared to %FGV from chemical decomposition of the whole breast.

Figure 5.

An example of the effects of the bias field on segmentation: (a) raw image with the bias field present; (b) bias-field-corrected image produced by the CLIC method; (c) tissue classification using the FCM method on the raw image; (d) tissue classification using the CLIC method.

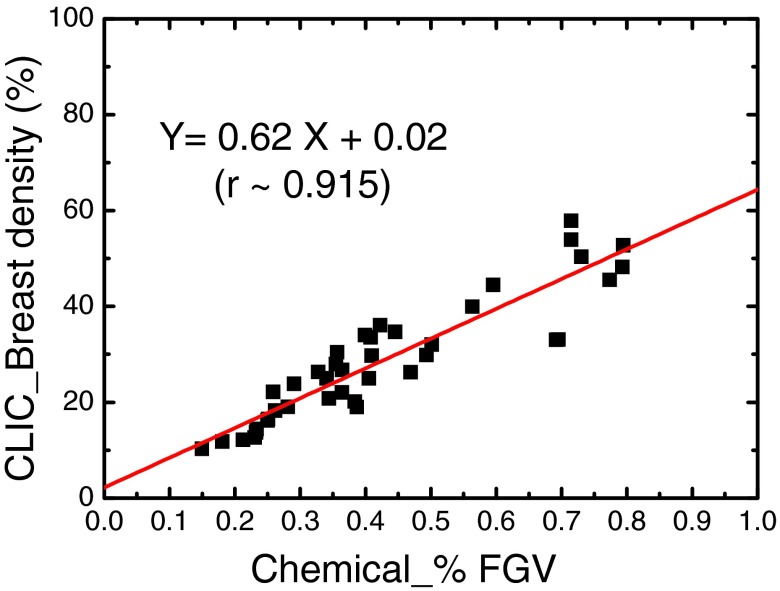
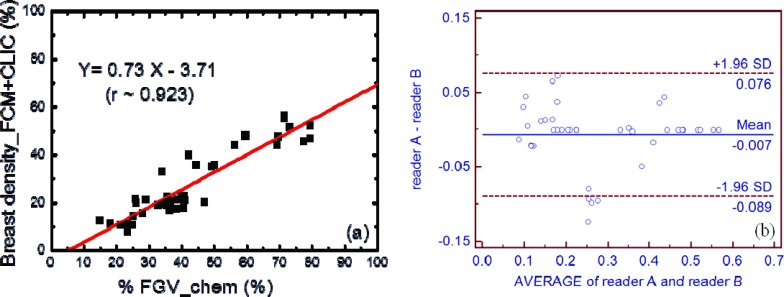
The correlation between breast densities estimated from the CLIC method and chemical decomposition (%FGV) is shown in Fig. 6. After the correction of the bias field, the Pearson's r increased from 0.86 to 0.92. The SEE was also reduced from 8.2% to 6.5%. The results of the FCM segmentations on the bias-field-corrected images are shown in Fig. 7. The breast density and %FGV correlations obtained by the two independent readers were very similar. Here, the result from one of the readers is presented in Fig. 7a. The linear correlation coefficients from the two readers were estimated to be approximately 0.92 and 0.90, respectively, which sets the limit for the variations induced by the subjective nature of the semiautomatic FCM segmentation method. More importantly, since the same tissue segmentation technique was used before and after bias field correction, as shown in Figs. 47a, respectively, the difference in the linear correlation can be used to show the effect of bias field correction on breast density quantification. It was shown that the linear correlation between breast density and %FGV has been improved after bias field correction. To further evaluate the inter-reader variation induced by the semiautomatic nature of the FCM segmentation method, a paired t-test was performed on the breast density measurements from the two independent readers, with a null hypothesis that the population means are the same. A p-value of 0.70 was obtained, suggesting that there is no significant difference from the two segmentation results. The Bland-Altman plot of the two measurements is shown in Fig. 7b. It can be seen that the bias between the two readers is almost negligible. Only four out of the 40 breasts processed by the two readers showed a breast density difference that is outside the 95% confidence interval.

Figure 6.

The correlation between breast densities measured with the CLIC method and the %FGV from chemical analysis. The linear fitting is shown as the straight line. The Pearson's r is estimated to be 0.92.

Figure 7.

(a) The correlation between breast densities measured with the FCM method on the bias-field-corrected images generated from the CLIC method and the %FGV from chemical analysis from one of the two readers. The linear fitting is shown as the straight line. (b) The Bland-Altman plot for the comparison between the results from the two readers. Only a small inter-reader variation was found in the FCM segmentation.

DISCUSSIONS

In this study, we investigated the feasibility of quantifying breast density with MRI images using automatic computerized algorithms. In particular, the effect of bias field in breast density quantification was evaluated by comparing the standard FCM clustering on the raw and bias-field-corrected images, as well as the fully automatic CLIC method which simultaneously estimated and corrected the bias field during the iterative process of tissue classification. Image nonuniformity could be due in parts to tissue degradation, but the majority of the contribution is likely to be from RF coil bias field because the spatial variations were consistent across all images. In order to have a reliable and quantitative system metric for the evaluation, we performed postmortem studies on 40 breasts. The major advantage of such a study is that it allows for a definitive compositional analysis through chemical decomposition. This provides a gold standard for an objective comparison, since the potential errors in chemical analysis can be controlled to be well below the required sensitivity.^{25, 32} Thus, it is the most straightforward way to evaluate the performance of an image-based segmentation algorithm. The results of this study suggest that although computer-assisted image segmentation based on a standard FCM algorithm can be used to estimate the volumetric breast density on breast MRI images, the presence of the bias field will reduce the accuracy of the tissue classification, and, in some cases, lead to significant errors in breast density quantification. Applying the same algorithm on the raw and the bias-field-corrected images increases the linear correlation coefficient from 0.86 to 0.92. The performance of the fully automatic CLIC algorithm was comparable to that of FCM on bias-field-corrected images, showing similar linear correlation with respect to %FGV from chemical analysis. The variation induced by the subjective assessment in the semiautomatic FCM method was estimated to be small, evidenced by the interobserver study on the bias-field-corrected image segmentation process. Therefore, the difference observed in the correlation coefficients can be attributed to the effect of bias field, which has to be estimated and corrected in order to achieve a reliable breast density measurement.

The left–right correlations of the glandular volume and the breast density were studied for the two computerized image segmentation methods. Such correlations have been used in clinical studies to evaluate the precision and the consistency of the methods.³³ The breast densities of the left and right breast from the same individual are expected to be similar, under normal conditions. Our chemical analysis of the postmortem breast samples also suggests an excellent match for the breast densities in the left and right breasts from the same pair.³² In the image segmentation studies, both methods yielded a slope very close to 1, suggesting a relatively good precision in breast density estimation. It should also be noted that the CLIC method performed better than the standard FCM method, which did not correct for the bias field, as exhibited by the negligible intercept and higher correlation coefficient. The effect of bias field correction is more significant in the left–right correlation of the glandular volumes. The slope of the linear fit increases from 0.71 to 0.94 after the intensity inhomogeneity induced by bias field was corrected by the CLIC method. The relatively poor Pearson's r of approximately 0.7 from the standard FCM method indicates the great challenges induced by the bias field for computerized clustering algorithms. This may be attributed to the fact that, when a pair of breasts was scanned at the same time with one RF coil, the presence of the low spatial frequency bias field alters the pixel values in the two breasts. Before bias field correction, the clustering program was not able to correctly segment the glandular tissue, which undermines the left–right volume correlation. After the issue of bias field has been properly addressed with the CLIC method, the Pearson's r of the left–right volume correlation was significantly improved, although it is still less than 0.90. However, unlike breast density, the glandular volume may not always match in the same breast pair. In fact, although most breast pairs had similar weights for the left and right breasts, a few breast pairs did have significantly different masses. This may be partly due to variations in sample preparation. Therefore, for the left–right volume correlation, on one hand, the slope of the linear fitting is still expected to be 1 due to volume consistency in most samples; on the other hand, the correlation coefficient is expected to be slightly reduced due to the presence of a few mismatched pairs. This agrees with what we have observed in the case of the CLIC algorithm.

The image-based segmentation algorithms quantify breast density by classifying each pixel as either glandular or adipose tissues. However, an accurate measurement of the glandular volume is very difficult, even with chemical analysis, due to the challenges in perfect tissue separation. Therefore, we proposed the use of a definitive measurement of tissue composition, in terms of the volumetric percentages of water, lipid, and protein, as a surrogate marker for breast density evaluations. The correlation between breast density and the %FGV has been studied with mammography, which confirms the linear relationship shown in Eq. 8.^{25, 34} Equation 8, which was derived under the assumption that the chemical compositions of pure glandular and pure adipose tissue are the same among all breast samples, results in a slope generally greater than 1 and a negative intercept. However, practically, water, lipid, and protein concentrations for the glandular and adipose tissues may vary in a small range as a Gaussian broadening.^{31, 35} The small variations will propagate to the slope and intercept estimations in a linear fitting. Thus, it is hard to predict the fitting parameters for the correlation between breast density and the %FGV, or to use them as an evaluation metric between different image segmentation algorithms. On the other hand, the correlation coefficient, i.e., Pearson's r, which is unaffected by the small variations in tissue compositions, can be used as a reliable system metric for quantitative comparisons.

In the present study, the correlation coefficient was improved after bias field correction for both the CLIC and FCM methods during the tissue classification process. One may also notice that the range of breast densities, especially on the high end, has been reduced. This can be attributed to the removal of those voxels that were mistakenly assigned to glandular in the presence of the bias field. The reduction of the glandular volume using the CLIC method can clearly be recognized in Fig. 5. After bias field correction, the breast densities of the 40 postmortem breasts ranged from approximately 8% to 57%, with an average value of 27.6%, which agrees well with the most recent estimates of clinical breast density.³⁶ It should be noted though that these numbers are volumetric measures of the breast density, which have a much smaller range than area-based measures such as the BIRADS classification of mammographic breast density.³⁷ We have also performed cone beam CT scans on the same postmortem breast samples to determine the breast density from the reconstructed 3D CT images. The range of breast densities measured by a standard FCM algorithm on the CT measurements is from 4% to 52%,³² which matches well with the result from the bias-field-corrected MRI images. However, using FCM directly on the raw images resulted in a breast density range from 9% to 87%, which clearly suggested an overestimation for some postmortem breasts due to the presence of the bias field. One concern about the quantitative analysis on 3D data sets is the partial volume effect. Generally, for a given imaging protocol, the recorded value in a particular voxel depends on the tissue composition in the corresponding volume. If the voxel contains a single tissue type, the signal will be characterized by that tissue type. However, the presence of more than one tissue type will lead to partial volume effect, where the signal depends on the combined contribution from all tissues. The impact of partial volume effect is particularly important for MRI, as the voxel size is generally much larger than that of CT. Studies have shown that ignoring this effect in MRI by establishing binary voxel-based segmentations introduces significant errors in quantitative measurements.^{38, 39} Most of these errors are associated with accurate quantification of small volumes, such as lesions, where the boundary contributes significantly in the total volume estimation. In the current breast density study, however, the quantification was carried out by averaging a large number of voxels, where the partial volume effects may be largely alleviated. It should also be noted that the impact of partial volume effect becomes more significant as the surface to volume ratio increases. Therefore, the error induced from such effect would be higher in cases where the glandular tissue is distributed more sparsely in the breast. Finally, as compared to a similar CT breast density study,³² the correlation coefficient and SEE with respect to the %FGV from chemical analysis are slightly worse for MRI segmentation after bias field correction. This may be partly attributed to the partial volume effect as a result of larger voxel size used in MRI than that of CT.

The endeavor to use volumetric radiographic breast imaging has been dramatically increased in recent years, because of the potential improvement in contrast resolution due to the elimination of the anatomical noise problem associated with mammography.⁴⁰ The use of MRI has been increasingly recommended for the detection and diagnosis of breast cancer.⁴¹ As a 3D imaging modality, MRI offers a great amount of valuable information to the radiologists. However, it also demands great efforts to process the information. In the case of breast density quantifications, an observer will be required to process hundreds of MRI images for each patient, rather than four images in standard two-view mammography. Therefore, computer-assisted automatic segmentation programs have to be developed to replace the current visual assessment and manual histogram segmentation methods. In addition, computerized algorithms help to remove the inter- and intraobserver variations in breast density assessment. A robust algorithm would provide a reliable and objective measure of the volumetric breast density. Both the FCM and CLIC algorithms investigated in this study have the potential to be implemented as fully automated methods for tissue segmentation. However, in this study, due to the presence of the bias field, the number of clusters used in the FCM algorithm and the assignment of the glandular clusters were accomplished manually using visual assessment. In contrast, the whole process for the CLIC method was fully automated without observer intervention. Although additional work may be done to automate the FCM method, as reported recently by Keller et al.⁴² on a clinical mammographic breast density study, the lack of bias field correction in image segmentation would still undermine the precision and accuracy of breast density quantification. Finally, the basic FCM algorithm had computation times from a few seconds to 10 s running on an Intel Xenon E5360 2.53 GHz processor. However, the computation time for the CLIC method ranged from 5 to 30 min for each breast due to the large variation in sample sizes. The algorithm was vectorized in MATLAB, and parts of the code that could not be vectorized were written in C and used as mex files. The computation time needs to be further improved by using a faster computer or using a graphics processing unit (GPU) for future clinical applications.

Bias field correction is one of the most difficult tasks in MRI image processing. Most of the current algorithms were developed for brain imaging.^{21, 22, 23} The implementation of these algorithms for breast MRI can be more challenging as a result of the increased FOV. Although N3 algorithm has been considered as an optimal method for intensity inhomogeneity correction by a recent review paper,¹⁷ a study on clinical breast images has shown that using N3 alone may still have problems in breast images, which cannot allow an accurate segmentation.¹⁸ The authors from that study also proposed a new bias field correction method by combining N3 with FCM, which was reported to be significantly superior to both N3 and FCM by themselves, and gave equivalent quality as CLIC algorithm in almost all patient images. The feasibility of using bias field correction methods other than CLIC is currently under investigation in our group. This will include the studies on the implementation of the combined method of N3 and FCM, as well as the N4 algorithm, which may solve some of the issues with the original N3 algorithm. Another ongoing study is on tissue segmentation for clinical breast images, where other anatomy, such as heart, pectoral muscle, and lung are also presented in the MRI images. In this case, the first step is to separate the breast from the body. This is usually done based on body landmarks for the initial cut, followed by boundary detection algorithms to define the posterior boundary based on chest wall muscle. A semiautomatic method based on FCM and N3 algorithms has been used to segment the breast region and B-spline fitting has been used to exclude the chest wall muscle in previous publications.^{15, 18} Generally, bias field correction is not needed for breast segmentation, as the process focused on boundary detection in a small region. However, the implementation of the bias-field-correction technique, such as the CLIC method, is extremely important for separation of dense tissue from adipose tissue within a relatively large field of view that covers bilateral breasts. There is no gold standard for the evaluation of the accuracy of a segmentation technique in a clinical study. Therefore, the validation of the investigated segmentation methods with the current postmortem study is crucial for future clinical applications.

In conclusion, we have investigated the feasibility of volumetric breast density quantification with two computer-assisted image segmentation methods on MRI scans of 40 postmortem breasts. The standard FCM method classified breast tissues into glandular and adipose based on the raw and bias-field-corrected MRI images, while the CLIC method directly estimated and corrected the intensity inhomogeneities induced by the bias field on the raw images during the iterative tissue classification process. The postmortem study allowed for a definitive measure of tissue composition from chemical analysis, which was used as the gold standard for breast density correlation comparisons. The precision and the accuracy of the segmentation algorithms and the effect of bias field were evaluated through left–right and breast density- %FGV correlations, respectively. The results of the current study suggest that the presence of the bias field in MRI introduces challenges in tissue segmentation with a standard FCM algorithm. It is therefore necessary to develop algorithms that can correct for the effect of the bias field. The CLIC method investigated in this study significantly increased the precision and accuracy of breast density quantification in MRI by effectively correcting the bias field. Such a fully automatic computerized algorithm may have great potential in clinical MRI applications.