Effects of MRTI sampling characteristics on estimation of HIFU SAR and tissue thermal diffusivity

Abstract

While the non-invasive and three-dimensional nature of magnetic-resonance temperature imaging (MRTI) makes it a valuable tool for high-intensity focused ultrasound (HIFU) treatments, random and systematic errors in MRTI measurements may propagate into temperature-based parameter estimates used for pretreatment planning. This study assesses the MRTI effects of zero-mean Gaussian noise (SD=0.0-2.0°C), temporal sampling (t_acq=1.0-8.0 s), and spatial averaging (Res=0.5-2.0 mm isotropic) on HIFU temperature measurements and temperature-based estimates of the amplitude and full width half maximum (FWHM) of the HIFU specific absorption rate (SAR) and of tissue thermal diffusivity. The ultrasound beam used in simulations and ex vivo pork loin experiments has lateral and axial FWHM dimensions of 1.4 mm and 7.9 mm respectively. For spatial averaging simulations, beams with lateral FWHM varying from 1.2-2.2 mm are also assessed. Under noisy conditions, parameter estimates are improved by fitting to data from larger voxel regions. Varying the temporal sampling results in minimal changes in measured temperatures (<2% change) and parameter estimates (<5% change). For the HIFU beams studied, a spatial resolution of 1×1×3 mm³ or smaller is required to keep errors in temperature and all estimated parameters less than 10%. By quantifying the errors associated with these sampling characteristics, this work provides researchers with appropriate MRTI conditions for obtaining estimates of parameters essential to pretreatment modeling of HIFU thermal therapies.

1. Introduction

For high-intensity focused ultrasound (HIFU) treatments to be broadly accepted in the clinic, progress must be made in patient-specific treatment planning, monitoring and control. A key component to this goal is accurate modeling of the bioheat transfer equation (BHTE) (Pennes 1948), for which investigators need accurate knowledge of the magnitude and spatial distribution of the ultrasonic specific absorption rate (SAR) and of tissue thermal properties (Roemer 1999). However, due to variations among and within different organs, variability across individuals, and limitations of treatment hardware or prediction software (Mahoney et al 2001, Payne et al 2011), the modeled SAR values and table thermal parameters used in the BHTE may cause significant errors in temperature calculations used to predict thermal dose.

Previous work has shown that a new analytical method for obtaining HIFU SAR from experimental temperature data is significantly more accurate than the traditional linear method (Guy et al 1974, Roemer et al 1985) and will be a valuable tool in assessing and improving SAR predictive software (Dillon et al 2012). This method estimates the amplitude of the focal SAR as well as its lateral full width at half maximum (FWHM). In addition to providing estimates for SAR amplitude and width, the method generates an estimate for thermal diffusivity of the tissue in the focal region. Utilizing these improved parameter estimates in the BHTE during therapy planning, monitoring and control has the potential to improve the efficacy and efficiency of HIFU thermal therapies.

In the past, estimation of thermal and acoustic properties from experimental temperatures was accomplished using thermocouples or thermistor probes (Guy et al 1974, Goss et al 1977, Parker 1983, 1985, Valvano et al 1984, Roemer et al 1985). More recent investigators have used thermistors (Kharalkar et al 2008) as well as infrared imaging (Milner et al 1996, Telenkov et al 2001, Bobkova et al 2010, Giridhar et al 2012), backscattered ultrasound imaging (Anand and Kaczkowski 2008, 2009) and magnetic-resonance imaging (Cheng and Plewes 2002, Dragonu et al 2009) for estimation of ultrasound intensities and thermal properties. The use of magnetic-resonance temperature imaging (MRTI) for HIFU thermal therapies and estimation of relevant parameters is extremely valuable since it can provide fully three-dimensional non-invasive temperature measurements in and around the focal zone. By utilizing the extensive data available from MRTI, significant improvements in estimating SAR profiles and tissue thermal properties should be possible.

Unfortunately, the MRTI acquisition process can introduce errors into temperature measurements which may be propagated into temperature-based estimations of tissue properties and treatment parameters, including SAR and thermal diffusivity. First, unavoidable noise in MR temperature measurements can have a marked effect on the accuracy of estimation methods. Second, the MR acquisition process necessitates measuring continuously changing temperatures over a finite time period and combining them into measurements ascribed to discrete time points. Finally, the spatially distributed temperatures are averaged to create discrete temperature measurements for each voxel. This spatial averaging may cause misrepresentation of temperatures and has already been assessed for its effect on temperature and thermal dose calculations (Todd et al 2011, O’Neill et al 2012).

This paper presents simulation and experimental results assessing the effects of MRTI noise, temporal sampling, and spatial averaging on HIFU temperature measurements and on estimation of SAR amplitude and FWHM, and thermal diffusivity. These three parameters are estimated using the analytical method of Dillon et al 2012. Several HIFU power deposition patterns are assessed with lateral FWHM values ranging from 1.2 mm to 2.2 mm, making these results applicable to a range of HIFU focal beam sizes and experimental conditions. By quantifying the errors associated with MRTI sampling characteristics, this work should provide researchers with an appropriate set of conditions for obtaining non-invasive accurate estimates of parameters essential to pretreatment modeling of HIFU thermal therapies.

2. Methods

2.1. Simulation of SAR and temperature data

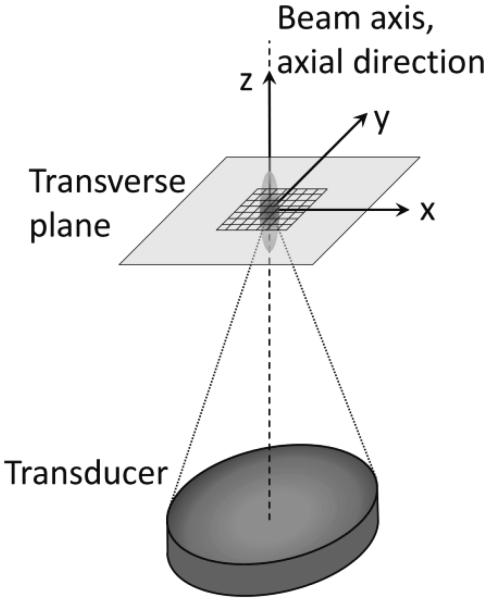
Simulated SAR patterns were generated by the hybrid angular spectrum method (Vyas and Christensen 2012) applied to a 256-element phased-array HIFU transducer and system (Imassonics, Besancon, France and Image Guided Therapy, Bordeaux, France) that was also used in experiments. The transducer had an aperture of 14.5 cm, frequency of 1 MHz, and radius of curvature of 13 cm. The simulated transducer power output was 10 acoustic watts focused 3-cm deep in the homogeneous tissue model, which had a tissue speed of sound of 1500 m/s, density of 1000 kg/m³, and acoustic pressure attenuation of 5.0 Np/m. These fixed values were used to generate the reference standard results for assessing the accuracy of estimates made from temperature data. The simulated SAR pattern had a lateral and axial FWHM of 1.4 mm and 7.9 mm, respectively, with a maximum SAR value of 15,300 W/kg. In both simulations and experiments, axial refers to the beam propagation direction (z) and terms laterral or transverse refer to directions perpendicular to beam propagation (x-y or r), as seen in figure 1.

Figure 1.

Orientation of coordinate axes in relation to the ultrasouund transducer and focal zone for simulations and experiments. The 7×7 voxel-fitting region used in each transverse plane and centered on the beam axis is also shown.

For each simulated SAR pattern, the BHTE was implemented in an explicit finite-difference (FD) solver to calculate temperatures for 32 s of heating. Thermal parameters used inn the model were thermal conductivity of 0.5 W/(m·°C), specific heat of 3500 J/(kg·°C), and density of 1000 kg/m³; thus, the thermal diffusivity reference valuue was κ=1.43×10⁻⁷ m²/s. Because the method will ultimately be applied in vivo, a Pennes perfusion coeffficient of 1.0 kg/(m³·s) was used in all simulations.

2.2. Simulation of MRTI noise

In simulations for the noise analysis, an isotropic grid spacing of 0.3 mm was used for generating FD temperatures with a temporal resolution of 0.1 seconds to maintain numeerical stability. Those temperatures were then undersampled to a 4.0-s temporal resolution, which is more representative of MRTI.

Following the undersampling of temperatures, zero-mean Gaussian noise was introduced to the simulated temperature data with standard deviations (SD) ranging from 0.5°C to 2.0°C, levels representative of noise in MRTI. The noise-free case was also analyzed for a refeerence comparison.

The estimation of parameters from these simulated temperatures is descrribed fully in section 2.5. Those estimations typically utilized a 7×7 voxel region of temperature-versus-time data centered about the beam axis in the transverse plane (figure 1). For the noisy temperature data, the parameters were also estimated using temperature data from 3×3, 5×5, 9×9, and 11×11 voxel-fitting regions. Noise introduction and parameter estimation was repeated 400 times for each noise level.

2.3. Simulation of MR temporal sampling

For temporal sampling studies, the 0.3-mm isotropic FD grid spacing was again used in temperature simulations for consistency. While this spatial resolution would be difficult to obtain experimentally, it is still appropriate because simulations for temporal sampling are independent of the FD grid spacing. In these simulations, the FD time step was varied to alter the temporal sampling as discussed below.

Measurements for a single 3-D volume of MR temperature images may take several seconds to acquire. Temporal sampling is a product of taking temperature measurements over this finite time period and attributing those temperatures to a single time point. The traditional method in which temperature data are temporally acquired and combined for proton resonant frequency MRTI (De Poorter et al 1995, Ishihara et al 1995) can be simulated with finite-difference and Fourier transform techniques.

First, temperature changes for a single FD time step (dt) are evaluated in a thermal model of the BHTE. The temperature changes are converted to phase changes and a constant magnitude (which does not affect temperature calculations) is added to the phase data to generate complex image data. Taking the Fourier transform of these complex images converts them to k-space. The data for the first line of k-space in the phase encoding direction are saved. The next time step of the thermal model is calculated, temperatures are again converted to k-space, and the second line of the k-space phase encoding direction is saved. The process is repeated until all of k-space is full. After a complete set of k-space has been saved, taking the inverse Fourier transform of those data will yield a complex image which can be converted to temporally sampled temperatures. Since the most significant information is found at the center of k-space, the temperature data are assigned to the simulation time at which data for the center of k-space was modeled and saved. With the next time step of the FD model, the first line of a new set of k-space data is saved and the process begins anew.

By varying the model time step dt, which is analogous to the MRTI pulse-sequence repetition time TR, the simulated MR acquisition time (t_acq) can be altered as

$$t_{acq}=dt\cdot nY,$$ (1)

where nY represents the number of k-space lines in the phase encoding direction. In this analysis, the time step dt was varied so that acquisition times of one to eight seconds could be achieved, times representative of the current capabilities of 2-D and 3-D MRTI. These simulations assume that the ultrasound start time is synchronized with the start of MR image acquisition, which is easily accomplished by pulse sequence triggering in the MR-guided HIFU system.

The parameter estimations for temporal sampling simulations, described in detail in section 2.5, used as many data points from the temperature-versus-time curves as were available for the 32 s of heating. Note that with longer acquisition times fewer data are available for fitting: for t_acq=1.0 s, 32 data points are available from each temperature-versus-time curve, whereas for t_acq=8.0 s, only four points are available in each curve.

2.4. Simulation of MR spatial averaging

For spatial averaging, the initial grid spacing for temperature simulations was set at 0.1-mm isotropic. The time step of the FD solver was 0.01 s for stability, and the data were undersampled to 4.0 s per measurement. These data were then spatially averaged with an algorithm that mimics the spatial averaging of MRTI (Todd et al 2011). Since the size of the focal zone plays a significant role in the errors induced by spatial averaging, simulations were generated for several different focal zone sizes with the lateral FWHM measurements varying from 1.2 mm to 2.2 mm in addition to the reference FWHM of 1.4 mm. Altering the size of the reference focal zone with the same ultrasound transducer was accomplished by adjusting the simulated transducer frequency while keeping the total attenuation constant at 5.0 Np/m. While adjusting the frequency to alter the focal zone size would not normally be applied in practice, doing so in simulations provides a variety of ultrasound power deposition patterns that could be used to assess errors of HIFU systems with different focal zone sizes.

Simulating the spatial averaging of MRTI requires temperature simulation data with very fine spatial resolution (0.1-mm isotropic). After changing the simulated temperatures to phase data, adding a constant magnitude term, and converting into k-space with a Fourier transform, the edges of k-space are masked to zeros. This masking causes the loss of the high frequency data in the k-space domain, which reduces the spatial resolution of the temperatures. In each direction that is masked, the ratio of the total original lines to the remaining unmasked lines will be the ratio of the new spatial resolution to the initial resolution. For example, a matrix size of 200×200×300 at an initial resolution of 0.1-mm isotropic could be masked with zeros except for the central 10×10×15 region, resulting in a resolution of 2.0-mm isotropic grid spacing since 200/10=300/15=2.0/0.1. Taking the inverse Fourier transform will convert the zero-filled k-space data back to complex images from which spatially averaged temperatures are calculated.

By zero-filling the k-space data, the spatially averaged temperature data will have the same grid spacing as the initial data but the spatial resolution will be altered. Essentially, the lower resolution data is being zero-filled interpolated so that the grid spacing remains unchanged.

For spatially averaged data, the parameter estimation methods used a subset of the final 0.1-mm grid spacing data. Data for the 7×7 voxel-fitting region were taken every 0.3 mm centered at the beam axis so the total region of data fitting was consistent for assessment of simulated noise, temporal sampling, and spatial averaging effects.

Since focused ultrasound beams are longer in the axial direction than in the transverse direction, the spatial distribution of temperature varies less in the axial direction. Because of this, high-resolution imaging in the axial direction is less important than in the transverse plane. Using a different ratio for the zero-filled mask in the k-z direction will change the resolution of the axial slices. In this study, after determining the isotropic resolution required for the reference focal zone, the voxel dimension in the z-direction was increased to assess effects of changing axial resolution while keeping the lateral voxel dimensions constant.

2.5. Estimation of SAR amplitude and FWHM, and thermal diffusivity

The analytical temperature solution used for the temperature-based parameter estimations assumes a 1-D radial Gaussian heating pattern (Parker 1983, 1985, Kress and Roemer 1987, Cheng and Plewes 2002, Dragonu et al 2009, Anand and Kaczkowski 2008, 2009) and that axial conduction and perfusion effects are negligible (Dillon et al 2012). The solution, at non-zero radial positions in the transverse plane, during heating is given by

$$T(r,t)=C\left(\frac{\beta }{4\kappa }\right)\left[Ei\left(\frac{-r^2}{\beta }\right)-Ei\left(\frac{-r^2}{\beta (1+4\kappa t∕\beta )}\right)\right],$$ (2)

where C=2αI₀/(ρc_p) and Ei represents the exponential integral. In term C, α represents the tissue acoustic pressure absorption coefficient, I₀ is the ultrasonic intensity on the beam axis, while ρ and c_p are the tissue density and specific heat, respectively. When the radial distance r from the beam axis and the time t since the onset of ultrasound heating are known, a least-squares three parameter fit of Eq. 2 to the simulated or experimental temperature data is possible by concurrently optimizing C, κ, and β. The fitting process utilizes temperatures from a 7×7 voxel-fitting region in a single transverse plane centered about the beam axis. The 7×7 region was selected because it includes data over the entire width of the ultrasound beam. Each of the 49 temperature-versus-time curves is fit to Eq. 2 simultaneously in a least squares manner, generating a single estimate for C, the thermal diffusivity κ, and the Gaussian variance β at each depth. Stepping through each transverse plane in the axial direction, the estimation process is repeated through the entire focal zone.

Because SAR is directly related to the initial slope of temperature rise, by taking the first derivative of Eq. 2 evaluated at t=0 and r=0, the maximum SAR amplitude in each transverse plane can be estimated from

$$SA{R}_{max}=c_{p}C.$$ (3)

The relationship between the Gaussian variance β and the estimated lateral FWHM of the SAR is given by

$$FWHM=2\sqrt{\beta \ln 2}.$$ (4)

Finally, an estimate for the tissue thermal diffusivity is found directly from fitting parameter κ at the depth of the global maximum SAR value, where the approximation of no axial conduction is most valid.

In the estimation of SAR amplitude, the only information required in addition to the temporal and spatial distribution of temperatures is the tissue specific heat capacity, which ultimately divides out when implemented in the bioheat equation. The tissue thermal diffusivity and FWHM of the ultrasound beam can be determined from the temperature data alone.

Due to the approximations of the 1-D radial Gaussian model, there are errors inherent to the estimation method prior to introduction of MR effects (Dillon et al 2012). Using this method in the absence of MR noise, temporal sampling and spatial averaging, for the reference focal zone size (lateral FWHM=1.4mm, axial FWHM=7.9 mm), maximum SAR is overestimated by 6-9%, FWHM is underestimated by 5-7%, and thermal diffusivity is overestimated by 2-6%. The effects of MR noise, temporal sampling, and spatial averaging upon estimation of SAR amplitude and FWHM, and diffusivity should therefore be considered with this initial offset in mind.

2.6. Experimental data

HIFU heating experiments were performed in ex vivo pork loin using the MR-compatible 256-element phased-array ultrasound system that was modeled in the simulation study, but operating at a power output of 8.8 acoustic watts. The maximum heating occurred 4.8 cm deep in the pork loin at the geometric focus of the ultrasound transducer. Deionized, degassed water coupled the ultrasound transducer to the pork loin sample.

For the reference case, images were acquired with a pair of two-channel surface coils built in-house at 1×1×3 mm³ resolution in a 3T Siemens Trio MRI scanner using a standard 3-D segmented echo planar imaging (EPI) sequence. Other imaging parameters included TR/TE=35/11 ms, FA=15°, bandwidth: 766 Hz/pixel, matrix: 192×108×10 (8 slices plus 25% slice oversampling), EPI factor=9, and a temporal resolution of 4.2 s per image volume. Imaging slices were oriented perpendicular to the axis of beam propagation in the transverse plane. Ultrasound heating was synchronized to begin with the acquisition of the fifth MR image and measurement times were assigned to the halfway point of each MR acquisition. The total heating time was 42 s. Temperatures were reconstructed using a reference-less (Rieke et al 2004) proton resonance frequency method (De Poorter et al 1995, Ishihara et al 1995) and post-processed with zero-filled interpolation to yield 0.5-mm isotropic voxel spacing (Todd et al 2011).

To confirm both system stability and that the pork loin’s thermal and acoustic properties were unchanged through the experiment, a total of four reference runs were interleaved between the heating runs used to assess the effects of temporal sampling and spatial averaging. Final reference results are combined and presented as the mean and standard deviation of these runs. A cooling period of 6-10 minutes was utilized between each heating run to ensure a uniform baseline temperature profile at the start of each ultrasound heating. Because the estimation method is based on changes in temperature, any increase in the baseline temperature from thermal accumulation in the tissue should not affect results.

To assess spatial averaging changes, the reference field of view in the lateral plane was doubled. This resulted in a spatial resolution of 2×2×3 mm³ while all other ultrasound and MR parameters were unchanged. To demonstrate effects of varied temporal sampling, the matrix size was increased to 192×162×10 (8 slices plus 25% slice oversampling) while maintaining the reference spatial resolution, thus altering the temporal resolution to t_acq=6.3 s per image volume. In this case, the total heating time was 44 s, slightly longer than the reference heating time. All other imaging and ultrasound parameters were kept the same as the reference case, and each set of temperature data was post-processed with zero-filled interpolation to 0.5-mm isotropic voxel spacing. The sampling characteristics of these MRTI data were selected to represent a practical and reasonable set of conditions that would be encountered in clinical, patient-specific applications.

In all cases, the axis of beam propagation (r=0) was found in each transverse slice by identifying the peak of a least-squares Gaussian fit to the radial temperature data from all images acquired during heating. Radial distances from the axis of beam propagation to the center of voxels in a square 7×7 region of interest (3.5×3.5 mm² centered on the beam axis) provided values for r in Eq. 2. At each depth, the 49 temperature-versus-time curves were fit with Eq. 2 simultaneously, minimizing the least-squares difference for all voxels at once and generating a single (planar) estimate for eacch parameter C, κ, and β. Assuming a pork specific heat of 2760 J/(kg·°C), the SAR amplitude was calcullated from Eq. 3 and the FWHM was estimated using Eq. 4. The tissue thermal diffusivity was determinned by parameter κ at the depth of the global maximum SAR.

3. Results

3.1. Simulated temperature-versus-time curves at maximum SAR location

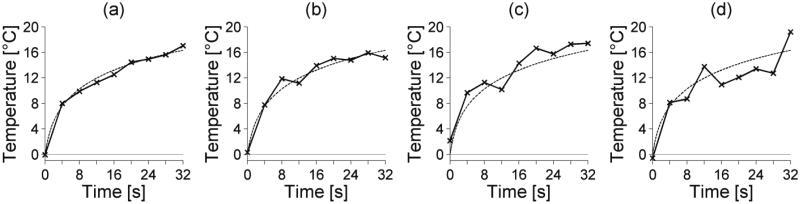
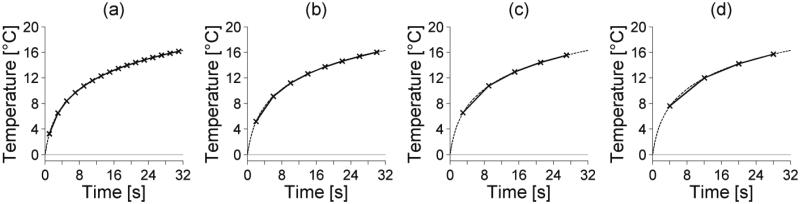
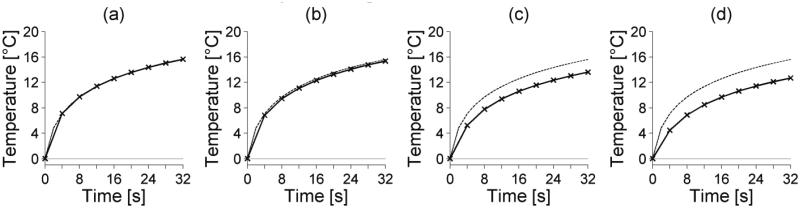
Figures 2, 3, and 4 show how noise, temporal sampling and spatial averaging, respectively, affect temperature-versus-time curves at the location of maximum SAR for the simulated reference case. In each plot, the unaveraged, noiseless temperatures are shown with dashed lines.

Figure 2.

Varying noise levels in simulated temperature-versus-time curves at the center of the focal zone. The standard deviation of the noise is (a) 0.5°C, (b) 1.0°C, (c) 1.5°C, and (d) 2.0°C. The dashed line represents the noiseless and unsampled FD temperature-versus-time curve.

Figure 3.

Temporal sampling effects on simulated temperature-versus-time curves at the center of the foccal zone. The simulated MR acquisition time is (a) 2 s, (b) 4 s, (c) 6 s, and (d) 8 s. The unaveraged FD temperature-versus-time curve is shoown as a dashed line.

Figure 4.

Spatial averaging effects on simulated temperature-versus-time curves at the center of the focal zone. The simulated isotropic spatial resolution is (a) 0.5 mm, (b) 1.0 mm, (c) 1.5 mm, and (d) 2.0 mm. The unaveraged FD temperature-versus-time curve is shown as a dashed line.

3.2. Parameter estimation: MRTTI noise simulations

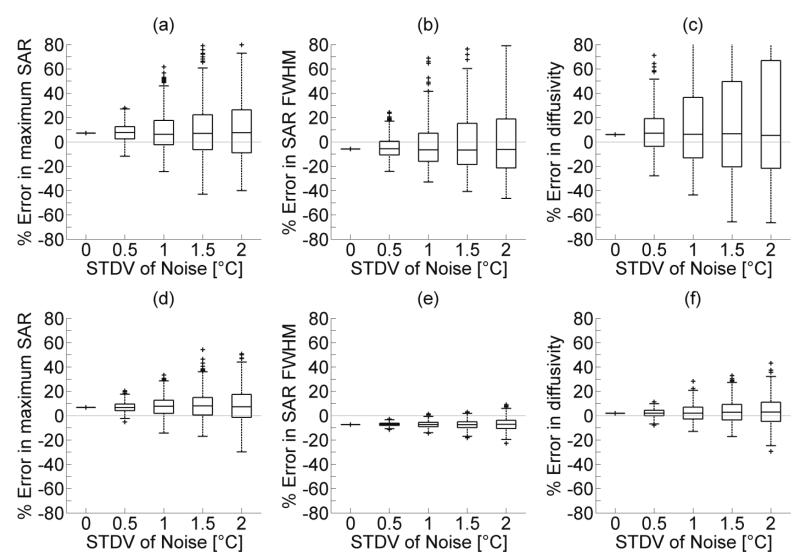
Errors in the estimated maximuum SAR, SAR FWHM, and thermal diffusivity for 400 simulations of noisy temperature data at each noise level are shown in figure 5. The horizonntal line within each box represents the median SAR error and box boundaries indicate the 25^th and 75^th percentiles. Whiskers extend to the most extreme data values or 1.5 times the interquartile range (IQR). Any values beyond 1.5 times the IQR are outliers marked with a plus sign. In each case, as noise levels increase, the spread of parameter estimation values also increases.

Figure 5.

Effects of simulated MR noise on parameter estimation of (a&d) maximum SAR, (b&e) SAR FWHM, and (c&f) thermal diffusivity. Figures 4(a-c) use temperature data from a 3×3 voxel-fitting region while figures 4(d-f) use temperature data from a 7×7 voxel-fitting region for parameter estimation. Simulations were repeated 400 times at each noise level and box plots include the median value (midline), upper and lower quartiles (box boundaries), with whiskers extending to the most extreme values or 1.5 times the IQR. Plus signs indicate outliers.

Figures 5a, 5b, and 5c use temperature-versus-time data from a 3×3 voxel-fitting region simultaneously for each estimation while figures 5d, 5e, and 5f use a 7×7 voxel-fitting region centered on the beam axis. For high levels of noise (SD=2°C), table 1 shows that increasing the number of temperature-versus-time curves for fitting reduces the IQR of estimates for maximum SAR, SAR FWHM, and thermal diffusivity.

Table 1.

Errors of estimated SAR amplitude and FWHM, and thermal diffusivity for different voxel-fitting regions. Simulations repeated 400 times with a noise standard deviation of 2°C. Errors are presented as the median percent error of the 400 simulations and the breadth of the interquartile range.

Size of voxel- fitting region	Maximum SAR Median % Error (IQR)	SAR FWHM Median % Error (IQR)	Thermal diffusivity Median % Error (IQR)
3×3	7.6 (35.4)	−6.3 (40.2)	5.4 (88.7)
5×5	8.2 (21.8)	−7.0 (9.4)	4.6 (23.3)
7×7	7.2 (18.9)	−7.2 (6.7)	3.0 (15.8)
9×9	7.5 (18.2)	−7.3 (6.1)	2.4 (13.1)
11×11	8.3 (17.6)	−6.9 (6.3)	6.0 (11.2)

3.3. Parameter estimation: MR temporal sampling simulations

While not shown, variation in errors caused by simulated temporal sampling were less than 5% for temperatures and all parameter estimates. In temperature measurements at the location of maximum heating, errors were less than ±1%. Errors in maximum SAR estimation ranged from 6.6% error for t_acq=1 s to 11.3% error for t_acq=8 s. Errors in FWHM estimation ranged from −8.5% to −9.4% for the same acquisition times. Diffusivity was overestimated consistently, ranging from 1.7% overestimation for t_acq=1 s to 5.8% for t_acq=8 s.

3.4. Parameter estimation: MR spatial averaging simulations

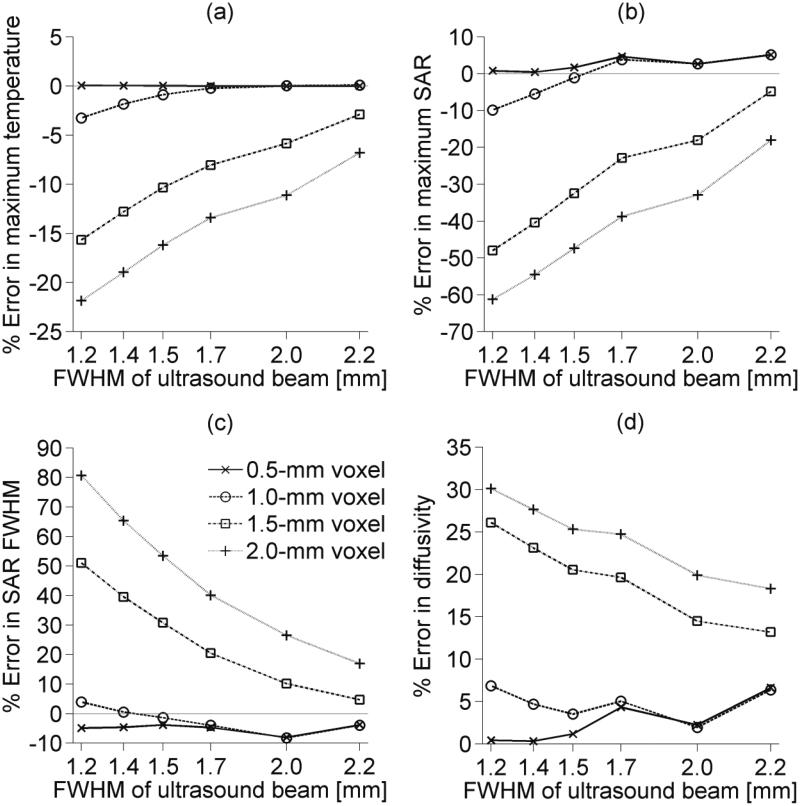
Simulated MR spatial averaging results for several HIFU focal zone sizes with lateral FWHM measurements ranging from 1.2 mm to 2.2 mm are presented in figure 6. Figure 6a shows that spatial averaging causes temperature measurements to be lower than the unaveraged values. Plots are only shown are for the location of maximum heating, where errors are the largest, though temperatures are underestimated throughout the focal zone. Using those inaccurate temperature measurements in parameter estimation generally leads to underestimation of maximum SAR (figure 6b) and overestimation of the SAR FWHM (figure 6c) and tissue thermal diffusivity (figure 6d). For the HIFU focal zone sizes studied, an isotropic voxel spacing no larger than 1.0 mm is required to measure the maximum temperature rise with less than 5% error. Using 1.0-mm isotropic voxel spacing also keeps all parameter estimation errors less than ±10% for beams with a lateral FWHM less than 2.2 mm.

Figure 6.

Simulated spatial averaging errors for varied isotropic voxel spacings and ultrasound focal zone sizes. (a) shows errors in spatially averaged temperatures at the location of maximum heating, while parameter estimation errors caused by spatial averaging are shown in (b) for maximum SAR, (c) for estimated beam FWHM, and (d) for thermal diffusivity.

3.5. Parameter estimation: Non-isotropic spatial averaging simulations

Though these simulation results are not shown, for the reference focal zone size (lateral FWHM=1.4mm, axial FWHM=7.9 mm) with a transverse voxel dimension of 1×1 mm², the axial voxel dimension can be increased from isotropy up to 3 mm without affecting the accuracy of temperatures and estimates of SAR amplitude and FWHM, and thermal diffusivity. The axial voxel dimension can bee increased up to 4.3 mm with errors in temperature, FWHM and diffusivity estimates still less than ±10%, and errors in SAR amplitude less than 20%. At 5 mm for the axial voxel dimension, errors in temperature deviate from the isotropic case by more than 10% and subsequent errors in parameter estimation can be affected by as much as 25%.

3.6. Experimental temperature results

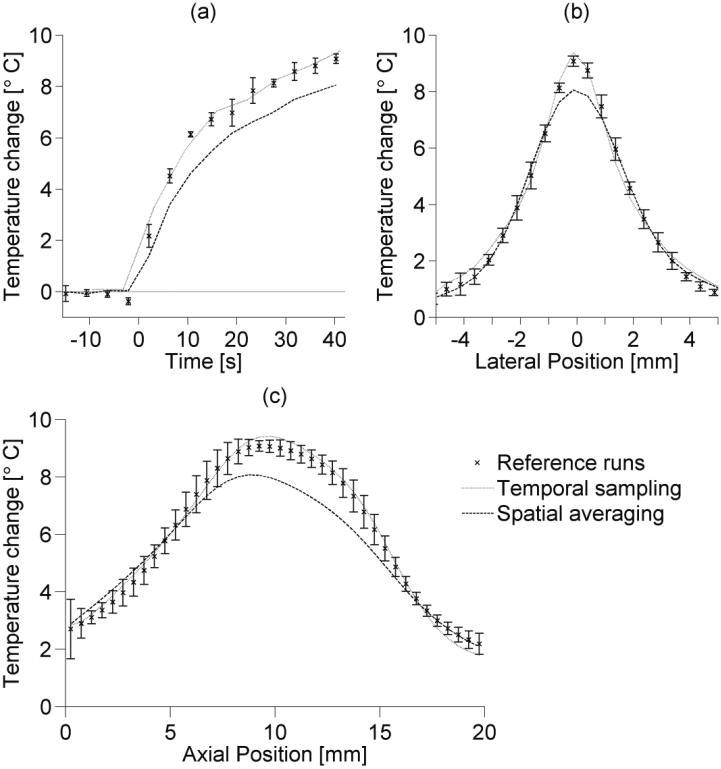
Figure 7 compares the temperature rise results from the reference experimental ruuns (1×1×3 mm³, t_acq=4.2 s) with altered temporal samplinng (1×1×3 mm³, t_acq=6.3 s) and spatial averaging (2×2×3 mm³, t_acq=4.2 s) cases. Error bars on reference teemperatures extend to plus or minus one standard deviation. Figure 7a is a temperature-versus-time plot at a the location of maximum heating within the foccal zone. The maximum temperature rise measured in the focal zone for the reference runs (N=4) had a mean of 9.15°C with a standard deviation of 0.18°C. For the temporal sampling and spatial averaging cases, the maximum measured temperature rises weere 9.42°C and 8.07°C, respectively. Those maximum temperatures occurred in the final measurements acquired during heating, at 40.2 s for thhe reference and spatial averaging cases and at 41.2 s for the temporal sampling case. Figures 7b and 7c show the lateral and axial temperature profiles through the focal zone at those times. Noise levels in temperature measurements for the reference, temporal sampling, and spatial averaging cases had a standard deviation of 0.26±0.01°C, 0.23°C, and 0.10°C, respectively.

Figure 7.

Experimental temperatures for reference runs (1×1×3 mm³ spatial resolution, t_acq=4.2 s), temporal sampling data (1×1×3 mm³ spatial resolution, t_acq=6.3 s), and spatial averaging data (2×2×3 mm³ spatial resolution, t_acq=4.2 s) in ex vivo pork loin. (a) is a temperature-versus-time curve at the location of maximum heating, while (b) and (c) are respectively lateral and axial temperature profiles from the last measurements of the ultrasound heating. Error bars (N=4) extend to ±1 standard deviation of the reference temperature data. Lateral positions are measured from the beam axis and axial positions are measured from the imaging plane nearest the transducer.

3.7. Parameter estimation: Experimental SAR, FWHM, and thermal diffusivity

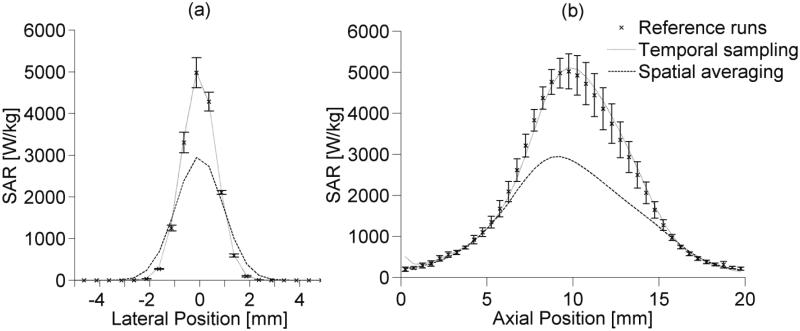
The estimated lateral and axial SAR profiles through the focal zone for the different cases are shown in figures 8a and 8b, respectively. Error bars mark one standard deviation above and below the mean value for the reference runs. Table 2 summarizes the experimental parameter estimation results showing the maximum SAR, SAR FWHM, a and thermal diffusivity values obtained by fitting Eq. 2 to the temperature data. Published values for pork loin thermal diffusivity range from 1.17×10⁻⁷ too 1.66×10⁻⁷ m²/s (Kent et al 1984, Sanz et al 1987).

Figure 8.

Experimentally estimated SAR profiles in ex vivo pork loin from reference, temporal sampling, and spatial averaging data in the (a) lateral and (b) axial directions. Error bars extend to ±1 standard deviation from the mean of reference runs. Lateral positions are measured from the beam axis and axial positions are measured from the imaging plane nearest the transducer.

Table 2.

Experimental parameter estimation results in ex vivo pork loin. Reference values are presented as the mean and standard deviation of estimates from the four reference runs.

	Maximum SAR [W/kg]	SAR FWHM [mm]	Thermal diffusivity [m2/s]
Reference mean (SD)	5023 (428)	1.56 (0.04)	1.44×10−7 (0.10×10−7)
Temporal sampling	5117	1.58	1.53×10−7
Spatial averaging	3148	2.21	1.79×10−7

4. Discussion

The primary finding of this study is that the accuracy of parameter estimates using the analytical method of Dillon et al 2012 is strongly dependent upon the accuracy of MRTI temperature measurements, which are influenced primarily by the degree of spatial averaging. Errors in temperature measurements caused by the MRTI acquisition processs are not only propagated, but are exacerbated when those temperatures are utilized for SAR and diffusivity estimation. Temporal sampling of temperature data caused by MRTI had little effect on temperatures or parameter estimation. Estimation errors caused by noise in temperature measurements, whille unavoidable, can be reduced by fitting with a voxel region that covers the entire focal zone.

4.1. MRTI noise

The simulation results of figure 5 show that utilizing temperature-versus-time data from a 7×7 voxel-fitting region, when compared with a 3×3 voxel-fitting region, significantly reduces both the incidence and magnitude of parameter estimation errors caused by noise. These results are even clearer from table 1; the more than fivefold increase in data of the 7×7 region compared to the 3×3 region reduced the IQR of maximum SAR, FWHM, and thermal diffusivity estimation error by 47%, 83%, and 82%, respectively.

While increasing the number of voxels for parameter estimation reduces errors, it also creates an increased computational burden during the fitting process. For example, parameter estimation for 40 slices of experimental temperature data using a 3×3 voxel-fitting region per slice took 26 s to compute in MATLAB on an Intel Core 2 Duo Processor T6500 at 2.1 GHz with 4.00 GB of RAM, while estimation for the same slices using data from a 7×7 voxel-fitting region took 144 s. In addition, voxels added to the fitting process are increasingly distant from the beam axis, their temperature changes are smaller, and noise makes up a larger portion of the overall temperature signal. In brief, there exist diminishing returns from increasing the number of fitting voxels in efforts to decrease noise-induced errors. Finding the appropriate balance between error reduction, computation time, and temperature signal-to-noise ratio becomes an important aspect in determining the number of voxels used in fitting for SAR amplitude and FWHM, and thermal diffusivity estimation. A good rule of thumb may be to only include voxel locations that are between the first zeros of the lateral SAR profile.

Increasing the time used to reach a certain temperature for parameter estimation could also mitigate the effects of noise. While Dillon et al 2012 showed that increasing the number of data points from each temperature-versus-time curve in the absence of noise did not significantly change the accuracy of SAR estimation, that is not the case for noisy temperature data. Just as increasing the number of voxels for fitting improves parameter estimation, increasing the number of data points in each temperature-versus-time curve introduces additional useful data to the fitting process, helping to reduce noise-induced errors in SAR amplitude, SAR FWHM, and diffusivity estimation. In this sense a longer heating time at a lower power during pretreatment sessions would allow more data points for fitting, reduce noise-induced errors, and provide more accurate estimations of the beam FWHM and tissue thermal diffusivity. Based on the results of Dillon et al 2012, the SAR could be scaled directly from these low-power pretreatment pulses to the higher powers to be used in the ablative treatment. It should be noted that accurately scaling SAR in this manner is limited to the linear acoustic propagation regime. At higher powers that could induce cavitation, non-linear effects can lead to enhanced heating, significantly changing the SAR distribution in addition to generating sharp temperature spikes which are difficult to measure with MRTI (Khokhlova et al 2009).

4.2. MR temporal sampling

The effects of temporal sampling upon MRTI temperatures appear to be minimal based on both simulation and experimental results. From simulated temperature and parameter estimations (section 3.3), there is a small decrease in accuracy with increasing acquisition time (<5% change). Because no ground truth temperature measurements are available for the experimental results and the actual parameter values are unknown, only trends in the experimental results can be commented upon. Comparing the reference experimental runs (t_acq=4.2 s) with the temporal sampling run (t_acq=6.3 s), there is no discernible change in the experimental temperature profile (figure 7) or parameter estimates (figure 8 and table 2), suggesting the minimal effect of temporal sampling.

It is known that the limiting factor in temporal sampling of MR temperature measurements is the rate of change of the temperature slope dT/dt. In this study, because the ultrasound is triggered to turn on and off in synchronization with the MRTI acquisition, the temperature slope does not vary enough within each measurement to greatly affect temperature measurements.

The standard progression through k-space for temporal sampling described in section 2.3 is not the same as the segmented EPI progression used in the experiments. In a segmented EPI sequence, k-space is divided uniformly into a number of segments determined by the EPI factor. One line of k-space in the phase encoding direction is acquired in each EPI segment for each pulse-sequence repetition time TR, effectively reducing the total MR acquisition time (t_acq) by the EPI factor. Because the EPI factor must be an odd number, data at the center of k-space, which is most significant, is always acquired at the midpoint in time of the image acquisition and progression through the central region of k-space does not include discontinuities that may occur at the transition between EPI segments. This matches the standard progression through k-space and additional simulations using the segmented EPI progression showed very little change in the temperature profiles (<±1 % difference) when compared with the standard k-space progression simulations.

One of the significant benefits of this estimation method is that the temporal resolution of temperature measurements plays such a limited role in the accuracy of parameter estimates. The traditional linear method for SAR estimation, on the other hand, has been shown to require temporal resolutions that are not currently feasible with three-dimensional MRTI (Dillon et al 2012). These results suggest that increasing the acquisition time per image to improve spatial resolution or minimize noise would be a useful approach for obtaining more accurate parameter estimates. However, a longer acquisition time would also generate fewer data points for fitting over the same heating period which may offset some of the gains from this approach. In other situations beyond parameter estimation, such as for thermal dose calculations, heating control and minimization of total treatment time, a short acquisition time is important so adjusting the temporal resolution should be used judiciously.

4.3 MR spatial averaging

Figure 6 shows that temperature errors caused by spatial averaging led to magnified errors in estimation of SAR amplitude and FWHM, and thermal diffusivity. A 15% error in the maximum temperature measurement could lead to SAR amplitude, SAR FWHM, and diffusivity errors of up to 50%, 50%, and 25% respectively. In order to obtain less than 5% error in temperatures and less than 10% error in parameter estimations using isotropic voxels, a 1-mm voxel dimension is necessary for the HIFU focal zone sizes (lateral FWHM=1.2-2.2 mm) assessed in this study.

With current imaging methods, obtaining MR temperature measurements at 1-mm isotropic resolution introduces significant noise. Simulations for the reference focal zone size (lateral FWHM=1.4 mm, axial FWHM=7.9 mm) suggest that an axial voxel dimension of 3 mm with transverse plane voxel dimensions of 1×1 mm² will produce temperature measurements nearly identical to those obtained from 1-mm isotropic voxels. Parameter estimation of SAR amplitude and FWHM, and thermal diffusivity are also unaffected by using 1×1× 3 mm³ voxels in place of 1×1×1 mm³ voxels. The stronger MR signal present from using these larger voxels should significantly reduce noise errors without introducing spatial averaging errors.

Trends in the experimental results support simulation results and highlight the importance of the degree of spatial averaging in MR-guided HIFU treatments. Peak experimental temperature measurements in the focal zone decreased by 12% when voxel spacing was increased from 1×1×3 mm³ to 2×2×3 mm³. Simulation results suggested those temperature measurements would decrease 10-17% (figure 6a). Experimental estimates of thermal diffusivity from temperature data obtained with 2×2×3 mm³ voxel spacing do not fall within the range of published data on pork loin thermal diffusivity (Kent et al 1984, Sanz et al 1987). The spatially averaged diffusivity estimates were 24% higher than the mean of reference estimates (table 2). This overestimation coincides with predicted simulation errors (figure 6d). Estimation differences between spatially averaged and reference data for SAR amplitude (-37%) and FWHM (42%) also correspond to anticipated errors from simulation data (figure 6b-c).

4.4. General observations

While this estimation method is intended to be used primarily in pretreatment planning, other applications are worth noting. Estimated SAR values could be used in the validation of ultrasound prediction techniques that include scattering, which is often neglected in current modeling practice. During therapeutic sessions, this method could be applied quickly for verification of pretreatment modeling and tissue property values if the pre-sonication temperature distribution is relatively uniform. The temperature fitting process could also be applied to forward-predict temperature and thermal dose profiles for improved control and monitoring.

The power deposition patterns used in this study are specific to the HIFU phased-array system used in simulations and experiments. However, many other HIFU systems have similar power deposition patterns and conclusions of this study may likely be applied without introducing significant errors. In particular, the different focal zone sizes assessed for spatial averaging effects demonstrate that the conclusions based on our reference focal zone size (lateral FWHM=1.4 mm, axial FWHM=7.9 mm) should be applicable to different systems and power deposition patterns. Inclusion of larger voxel-fitting regions to reduce noise effects would apply to any HIFU system. As discussed previously, temporal sampling is primarily a function of the rate of change of the temperature slope dT/dt, and would not be greatly affected by the application system.

The applicability of this estimation method is limited to the focal region. However, in the implementation of MRgHIFU for thermal therapies, temperatures and thermal dose in the near and far fields provide important safety constraints and should be considered in pretreatment planning strategies. One possibility for obtaining near and far field SAR would be to implement this method for determination of the focal SAR profile and use it as a guide for optimizing ultrasound modeling software that includes near and far field heating. Alternatively, since the SAR distribution in the near and far field are generally more diffuse and uniform than in the focal region, the traditional linear method for finding SAR (Guy et al 1974, Roemer et al 1985) from experimental temperature data could be implemented in those regions.

There are additional potential MRTI acquisition errors that were not assessed in this study. However, effects of those errors can be inferred. A systematic bias in the reference temperature (for example, if the baseline temperature was 33°C instead of an assumed 37°C) would not affect these results since SAR, FWHM, and thermal diffusivity estimates are based upon changes in temperature and not the absolute magnitude of temperature as is the case in thermal dose calculations. An error in the scale of the phase to temperature conversion would cause proportional errors in SAR estimates but would not affect FWHM or thermal diffusivity estimation. Temperature errors caused by phase drift during the scan are mitigated by using reference-less reconstruction techniques (Rieke et al 2004). Measurement discrepancies caused by grid placement that puts the maximum power deposition at edges or corners of a voxel were not assessed. However, zero-filling to 0.5×0.5 mm² in-plane will sufficiently mitigate most measurement discrepancy (Todd et al 2011).

5. Conclusion

This study demonstrates that estimates of HIFU SAR amplitude and FWHM, and thermal diffusivity are highly dependent upon the accuracy of MRTI temperature measurements. Specifically, errors in temperature measurements due to spatial averaging may lead to significant errors in parameter estimation. From simulated and experimental MRTI results, it is recommended that for HIFU beams with a lateral FWHM between 1.2 and 2.2 mm, a spatial resolution of 1×1×3 mm³ or smaller is required to accurately measure focal temperatures and estimate the maximum SAR, SAR FWHM, and tissue thermal diffusivity. Temporal sampling results show that for the temporal resolutions studied, longer acquisition times may be used to improve spatial resolution or image SNR without adversely affecting temperature measurements or parameter estimation accuracy. Effects of noise in temperature measurements, while unavoidable, can be reduced by simultaneous fitting of more voxels in the transverse plane and including more data points from each temperature-versus-time curve.

The MRTI sampling standards identified in this study will lead to accurate estimates of SAR amplitude and FWHM, as well as tissue thermal diffusivity. Such tissue- and patient-specific results will improve the efficacy and accuracy of treatment planning, reduce treatment times, and increase clinical acceptance of and confidence in HIFU thermal therapies.

PACS

87.50.yt

Therapeutic applications

87.19.Pp

Biothermics and thermal processes in biology

87.80.Lg

Biophysical techniques (magnetic resonance techniques)

87.85.jc

Physical properties of biomaterials