Vision-based flight control in the hawkmoth Hyles lineata

Abstract

Vision is a key sensory modality for flying insects, playing an important role in guidance, navigation and control. Here, we use a virtual-reality flight simulator to measure the optomotor responses of the hawkmoth Hyles lineata, and use a published linear-time invariant model of the flight dynamics to interpret the function of the measured responses in flight stabilization and control. We recorded the forces and moments produced during oscillation of the visual field in roll, pitch and yaw, varying the temporal frequency, amplitude or spatial frequency of the stimulus. The moths’ responses were strongly dependent upon contrast frequency, as expected if the optomotor system uses correlation-type motion detectors to sense self-motion. The flight dynamics model predicts that roll angle feedback is needed to stabilize the lateral dynamics, and that a combination of pitch angle and pitch rate feedback is most effective in stabilizing the longitudinal dynamics. The moths’ responses to roll and pitch stimuli coincided qualitatively with these functional predictions. The moths produced coupled roll and yaw moments in response to yaw stimuli, which could help to reduce the energetic cost of correcting heading. Our results emphasize the close relationship between physics and physiology in the stabilization of insect flight.

1. Introduction

Like most high-performance aircraft, insects use feedback control to help stabilize their flight. The feedback control system of an aircraft serves to modify the airframe's natural flight dynamics, so as to correct any instabilities and improve overall flight performance. The feedback control systems of insects have presumably evolved in concert with their flight morphology to achieve the same ends, but physiological studies of insect flight control have been largely divorced from physical studies of insect flight dynamics. Recent efforts combining modelling approaches with measurements of motor outputs have begun to bridge this gap [1–8], but whereas the physiology of insect flight control is understood well from a mechanistic perspective, it remains poorly understood on a functional level. In this study, we characterize the optomotor response properties of hawkmoths experimentally, before relating these properties functionally to flight stabilization and control with the aid of a published model of hawkmoth flight dynamics.

Insects use a combination of visual and mechanosensory feedback to stabilize and control flight. For example, the antennae are used to sense airflow in most insects, and are involved in inertial sensing of body rotations in hawkmoths [9–11]. The optomotor response properties that we measure in this study are therefore only one part of a bigger picture, but they are an important part of that picture in hawkmoths, which rely heavily upon vision in flight [12–14]. In common with other flying insects, hawkmoths possess motion-sensitive visual interneurons that respond to the optic flow generated by relative motion of wide-field visual stimuli [15–17]. The spatio-temporal sensitivity of these neurons appears to be tuned to the behavioural characteristics of the species concerned. For example, the visual interneurons of hawkmoths which fly in daylight, or which hover, typically have a faster response and a higher spatial resolution than those of species which are nocturnal or which do not hover [15–17]. Our study species, Hyles lineata (Fabricius), is a mainly crepuscular pollinator of the nectar-producing flowers at which it hovers to feed, so we would expect its visual system to have a comparatively fast response. Such findings offer broad insights into the visual ecology of flight, but do not relate vision to the insect's flight dynamics in a quantitative way.

Free-flight studies obviously have an important part to play in understanding how optomotor responses function under normal closed-loop conditions, but while it is possible to manipulate the dynamics of a free-flying insect to some extent [18], an insect's control responses can be measured completely separately from its flight dynamics through tethering. Rigidly tethering an insect leaves its controller physiologically intact, but eliminates the flight dynamics that would normally close its feedback loops [19,20]. It is of course possible that the insect might somehow perceive that it was tethered, and that it might alter the physiological properties of its control system to compensate, whether through learning, feedback or neuronal adaptation. There is no empirical evidence of any systematic time variance in our data (see §3), so although we cannot completely eliminate the possibility that tethering affects the physiological properties of the control system, we interpret the responses that we measure under the premise that the insect does not alter the physiological properties of its control system when tethered. In other words, we interpret the functional properties of optomotor responses measured in tethered flight conditional upon the assumption that the controller continues to behave as if the sensory input that it receives were still being obtained under normal closed-loop conditions. It is important to note that assuming that tethering has no effect upon the physiological properties of the control system is not the same as assuming that tethering has no measurable effect upon the output of the control system. For example, an integral controller would be expected to saturate in the presence of any persistent non-zero deviation from the insect's commanded state that tethering might impose [20], but this does not appear to be an issue here, because the responses that we have measured are evidently not saturated (see §3).

Most optomotor studies of tethered flight have measured only a single component of the total force or moment produced in response to only a single component of rotation or translation of the visual field, and have presented visual stimuli that stimulate only a part of the visual field (see [21,22] for reviews). Here, we measure all six components of force and moment produced in response to rotation of the entire visual field about three orthogonal axes, and use these measurements to characterize the overall response properties of the optomotor control system. Frequency domain approaches have been used successfully to characterize optomotor responses in a number of other insects [1,3,7,8,12,14], and we follow the same basic approach here. Having characterized the optomotor responses experimentally, we use a published theoretical flight dynamics model [23–25] to predict the natural flight dynamics of the insect (i.e. the free motions of the uncontrolled system). Any unstable modes of motion in the natural flight dynamics of the real insect must be stabilized by feedback control, and we therefore use the natural modes predicted by the theoretical flight dynamics model to provide functional interpretations of the optomotor responses that we measure.

2. Experimental methods

2.1. Animals

Hyles lineata pupae were obtained from breeding colonies two or three generations removed from wild stock. Pupae were stored at 12°C until required, and were warmed to 26°C to induce eclosion. We used a total of 17 adults (body mass: 0.58 ± 0.17 g; body length: 33.7 ± 2.5 mm; wingbeat frequency: 41.1 ± 2.4 Hz; mean ± s.d.). Each moth was flown for the first time 2 to 3 days post-eclosion, and on up to 5 days in total. Moths were cooled to 4°C and placed on a chilled stage for tethering, using CO₂ anaesthesis if required. The dorsal surface of the thorax was cleared of scales, and bonded to an aluminium tether using cyanoacrylate. The tether was bevelled to reproduce the 40° body angle typical of hovering hawkmoths [26]. At the beginning of each experiment, the moth was weighed and given 0.5 h to acclimate to laboratory light levels and temperature (26°C). At the end of each experiment, the moth was removed from the simulator, weighed, fed honey solution until sated and then stored overnight at 12°C.

2.2. Experimental apparatus

We measured the forces and moments produced by H. lineata in response to moving wide-field visual stimuli (figure 1a). The moths were tethered to a six-component strain gauge balance (Nano17, ATI Industrial Automation, NC, USA), with constant voltage excitation provided by a signal conditioning amplifier (2210A, Vishay, NC, USA). The amplified signals were low-pass filtered at 1 kHz, and sampled at 10 kHz (PowerLab/16SP, ADInstruments, NSW, Australia). The moths were mounted at the centre of a 1 m diameter hollow clear acrylic sphere coated with rear-projection paint (Rear Projection Screen Goo, Goo Systems, NV, USA). Two data projectors with DC lamps (LT170, NEC, Japan) were retrofitted with specialized micromirror chipsets (ALP-2, ViALUX, Chemnitz, Germany), and used to project eight-bit greyscale 1024 × 768 pixel images at 144 Hz onto the surface of the sphere (see §2.4 for details of stimulus design). The light levels inside the sphere (80 lux) were similar to those which would be encountered by the moths around dusk. The moths were not provided with any extrinsic airflow, but the flows induced by their own wingbeat would have induced a significant airflow stimulus over the antennae, as is known to be the case during hovering [27].

Figure 1.

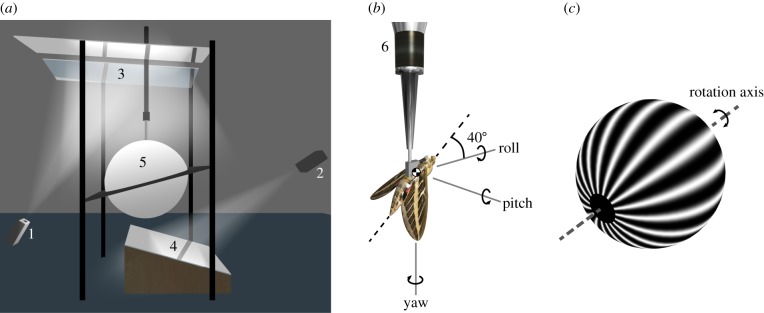
Overview of the experimental set-up. (a) Diagram of the virtual-reality flight simulator. Wide-field visual stimuli were provided by two modified data projectors (1,2) projecting via a system of mirrors (3,4), onto a hollow acrylic sphere coated with rear-projection paint (5). (b) The moth was tethered at the centre of the sphere to a six-component force–moment balance (6). The body axis system shown in the figure (see main text for definitions) was used to resolve the measured forces and moments, and was also used to define the axis of the visual stimulus. The angular velocity components shown here indicate the direction of self-motion of the moth corresponding to a positively signed visual stimulus in roll, pitch or yaw. (c) Diagram of the spherical sinusoidal grating used as a visual stimulus. The rotation axis of the grating was aligned with either the roll, pitch or yaw axis.

2.3. Axis systems

We used a right-handed axis system to define the moth's body axes, with the origin of the body axis system located at the centre of mass of the moth. We resolved the forces and moments in these body axes, and used the same set of body axes to describe the visual stimuli that we presented. The body axis system was oriented with its y-axis (i.e. pitch axis) normal to the moth's symmetry plane, and with its x-axis (i.e. roll axis) and z-axis (i.e. yaw axis) fixed by aligning the z-axis with the gravity vector when the moth was tethered (figure 1b). The same body-fixed axis system was used when modelling the flight dynamics, with the z-axis of the body axes fixed so as to be aligned with the gravity vector at equilibrium. For the purposes of the flight dynamics modelling, we used (u,v,w) and (p,q,r) to represent the (x,y,z) components of velocity and angular velocity relative to Earth-fixed axes. We defined the yaw angle (ψ), pitch angle (θ) and roll angle (γ) of the insect as the Euler angles of its body axis system, specified according to a (z,y,x) convention relative to Earth-fixed axes in which the z-axis was aligned with gravity.

2.4. Stimulus design

The visual stimuli were rendered using three-dimension modelling software (3ds Max, Autodesk, CA, USA). Each stimulus consisted of a spherical sinusoidal grating oscillated sinusoidally about its poles (figure 1c), which could be reoriented to simulate roll, pitch or yaw rotations (see figure 1b for axis definitions). The stimuli were designed to explore the effects of changing different visual motion parameters over a wide range of contrast frequency, defined as the number of pattern cycles per second passing each point in the moth's visual field. This is important, because the responses of the correlation-type motion detectors that are involved in insect motion vision depend fundamentally upon contrast frequency [28]. A quite different approach was taken by a recent study of abdominal responses in hawkmoths, which used visual stimuli designed to keep the peak angular velocity, and hence contrast frequency, of the stimulus constant [8]. This is a reasonable approach where the aim is to identify a linearized model of the flight controller, but will not excite any motion vision-dependent nonlinearities that may affect the overall system-level optomotor response. Because these nonlinearities may be functionally important, we designed our stimuli to explore the effects of contrast frequency, which may be at least as important in characterizing the optomotor system of an insect as the effects of temporal frequency that characterize linear systems.

The mean contrast frequency of a sinusoidal grating undergoing sinusoidal oscillation is proportional to the amplitude and temporal frequency of the oscillation, and the spatial frequency of the grating. We therefore presented three different sets of stimuli to the moths, varying each of these three parameters independently (table 1). In this first stimulus set, we presented a roll, pitch or yaw stimulus, varying the temporal frequency of oscillation between stimulus presentations, while holding the amplitude of oscillation and spatial frequency of the grating constant. In the second stimulus set, we presented only a roll stimulus, varying the amplitude of oscillation between stimulus presentations, while holding the temporal frequency of oscillation and spatial frequency of the grating constant. In the third stimulus set, we presented only a roll stimulus, varying the spatial frequency of the grating between stimulus presentations, while holding the temporal frequency and amplitude of oscillation constant.

Table 1.

Summary of stimulus set parameters.

stimulus set	rotation axis	temporal frequency (Hz)	oscillation amplitude (°)	spatial frequency (cycles per degree)
1	roll, pitch, yaw	1, 2, 3, 4, 6, 8, 12	5	0.05
2	roll	2	2.5, 5, 10, 20, 30	0.05
3	roll	2	5	0.025, 0.050, 0.100, 0.167, 0.333

We designed our stimuli to cover a range of stimulus frequencies and angular velocities up to and including the maxima at which hawkmoths have been shown to stop responding strongly to visual motion in electrophysiological [15–17,29,30] and behavioural [12–14,31] studies. The resulting stimuli covered the entire range of angular velocities over which the theoretical flight dynamics model was parametrized (see §4.1), with the fastest stimuli having a mean angular velocity of 240° s^–1 and peaking at 377° s^–1. The slowest stimuli that we presented had a frequency of 1 Hz, and although the moths would probably have responded to stimuli at lower frequencies, the resulting forces and moments would have been too small for us to measure reliably. Furthermore, the theoretical flight dynamics model predicted that the natural instabilities in the moths’ flight dynamics would have grown by three orders of magnitude over a single 1 Hz stimulus cycle (tables 2 and 3). Consequently, although the moths’ response to lower frequencies may be of relevance in guidance problems, such as station-holding at a flower, stimuli of lower frequency than those we presented would not have been relevant to the stabilization of the moths’ unstable flight dynamics.

Table 2.

Eigenvalues characterizing the longitudinal natural modes of motion of H. lineata predicted by the theoretical flight dynamics model.

	slow, unstable oscillatory mode	fast, stable monotonic mode	slow, stable monotonic mode
eigenvalue	7.72±16.38i	–19.92	–2.37
time to half/double (wingbeats)	3.7	1.4	12.0
frequency (Hz)	2.6	—	—

Table 3.

Eigenvalues characterizing the lateral natural modes of motion of H. lineata predicted by the theoretical flight dynamics model.

	slow, unstable monotonic mode	stable oscillatory mode	fast, stable monotonic mode
eigenvalue	7.88	–14.11 ± 9.10i	–84.38
time to half/double (wingbeats)	3.6	1.7	0.3
frequency (Hz)	—	1.4	—

2.5. Experimental design

Each stimulus set was presented as a block, to minimize the time between the different stimulus presentations being compared. The order of presentation of the blocks was randomized for each moth, as was the order of stimuli within each block. A roll stimulus with 2 Hz temporal frequency, 5° oscillation amplitude and 0.05 cycles per degree spatial frequency was presented between stimulus sets to serve as a reference to check for possible fatigue. Each stimulus was presented for long enough to enable recording of 60 s of flight. During the 30 s intervals between different stimulus presentations, the moths were presented with a static white background. Stimulus presentations were continued for as long as the moth continued to fly strongly, which we judged by eye during the experiments, looking for a stroke amplitude consistently greater than 90° during stimulus presentations.

2.6. Data processing

We discarded any recordings with obviously erratic variation in the peak forces, prior to downsampling the signals to 1 kHz, and converting the downsampled signals to forces and moments resolved at the estimated position of the centre of mass of the moth (see electronic supplementary material). The recordings of each force or moment component were normalized by body mass and transformed into the frequency domain using the chirp-Z transform [32,33] at frequency points from 0 to 60 Hz in 0.1 Hz steps, using Welch's method for window averaging with 80% overlapping Hanning windows of 8 s duration. This allowed us to compute the magnitude, phase and coherence of the response with reference to the angular position of the stimulus (see electronic supplementary material for further detail). Conceptually, the magnitude of the response measures the ratio of the output amplitude to the input amplitude at a given frequency, the phase of the response measures the phase difference between the output and the input at a given frequency, and the coherence measures the fraction of the power in the output spectrum that can be linearly attributed to the input spectrum at a given frequency [32,33]. We avoid referring to the response magnitudes as gains, because the units of input and output are different, so there is no special meaning to a response magnitude of 1 (i.e. 0 dB on a logarithmic scale).

Unsurprisingly, there was always a large peak in the output power spectrum at wingbeat frequency, but at frequencies less than 20 Hz almost all of the remaining output power was concentrated at the stimulus frequency (figure 2). This is a necessary, but insufficient, condition for linearity. In fact, as we show below, the system is fundamentally nonlinear. Consequently, although some of the graphs that we present resemble Bode plots familiar from linear systems analysis, they should not be interpreted as such. Instead, they should be thought of as graphical representations of describing functions approximating the full nonlinear system. A describing function is a quasi-linear approximation of a nonlinear system, which defines how input maps to output at the input frequency, as a function of input amplitude and frequency [34]. This is a reasonable way to approximate a nonlinear system if the harmonic content of the response is negligible, as is the case for our data (figure 2).

Figure 2.

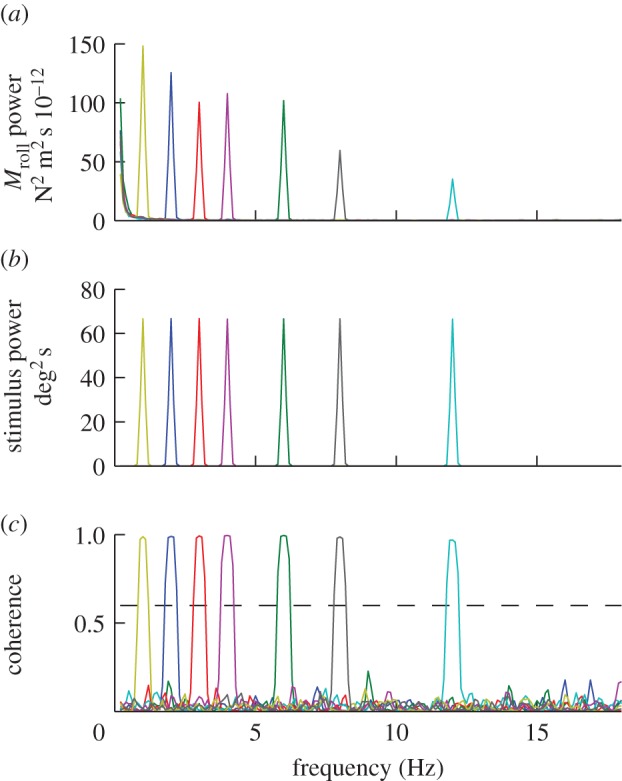
Power and coherence of the responses of a single moth to roll stimuli oscillating at different temporal frequencies. Each coloured line represents a different stimulus trial. (a) Output power spectra of the roll moments generated by the moth. (b) Input power spectra of the angular position of the visual stimulus. (c) Coherence of the roll moment response relative to the angular position of the visual stimulus.

We excluded responses with coherence less than 0.6 from further analysis, which is a recommended rule of thumb for quality control in aircraft system identification [33]. A total of 50 of 1040 stimulus presentations (i.e. less than 5% of recordings) were excluded by this criterion. For each moth in each stimulus condition, we computed the arithmetic mean of the response magnitude normalized by body mass, and the circular mean of the response phase. Finally, we pooled the mean responses of all of the moths and calculated their grand mean and standard error, using the appropriate circular statistics for phase [35].

3. Experimental results

Individual moths produced time-averaged flight forces that were usually close to body weight. The distribution of mean force production was skewed by the behaviour of a few weaker individuals, but the median of the means for all of the moths was 96% of body weight. Most moths had a tendency to generate a small nose-down pitch moment and a small excess of forward thrust, indicating that they were not quite at equilibrium. The moths modulated the forces and the moments that they produced in response to the stimuli that we presented, but as the effect of the measured forces would have been much smaller than the effect of the measured moments, we consider only the moment responses hereafter. The moths also modulated the orientation of their head and abdomen in response to the stimulus, but we treat these components of the moths’ optomotor response as part of a black box between the visual stimulus and the moments produced.

The analysis that follows treats the measured responses as time-invariant. We checked the appropriateness of this treatment in two different ways. First, we looked at the mean coherence of each of the measured responses, which we found to be high for all stimuli (typically greater than 0.8 over each stimulus presentation). This implies that the magnitude and phase of the responses were consistent within each stimulus presentation, from which we conclude that the responses cannot have been markedly affected by the phase of the wingbeat relative to the stimulus, which would have varied continuously through each recording. Second, we checked for possible changes in the response properties of the moths between the beginning and end of each stimulus presentation, by comparing the magnitude and phase calculated for the first and second halves of each recording. We found no systematic difference between them, from which we conclude that the moths had no general tendency to increase or decrease the magnitude or phase of their response between the beginning and end of each stimulus presentation.

3.1. Directional properties of the measured responses

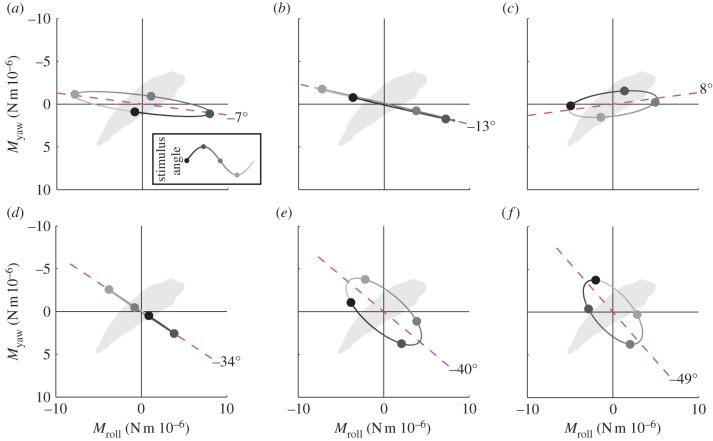
The moths responded to roll stimuli by producing large roll moments of the appropriate sense to counteract their apparent self-motion (figure 3a), together with smaller moments about the yaw axis (figure 3a). The accompanying pitch moments had low coherence (less than 0.6), so were not attributable to the roll stimulus. The yaw moment led the roll moment at stimulus frequencies less than 4 Hz, but lagged the roll moment at stimulus frequencies greater than 4 Hz (figure 3b). The cause of this variable phase relationship is unknown, but its consequence is that the total moment vector sweeps a narrow elliptical path through each roll stimulus cycle (figure 4a–c). We take the major axis of this ellipse to define the major axis of the moths’ response to roll stimuli, which was close to the roll axis at all stimulus frequencies (figure 4a–c).

Figure 3.

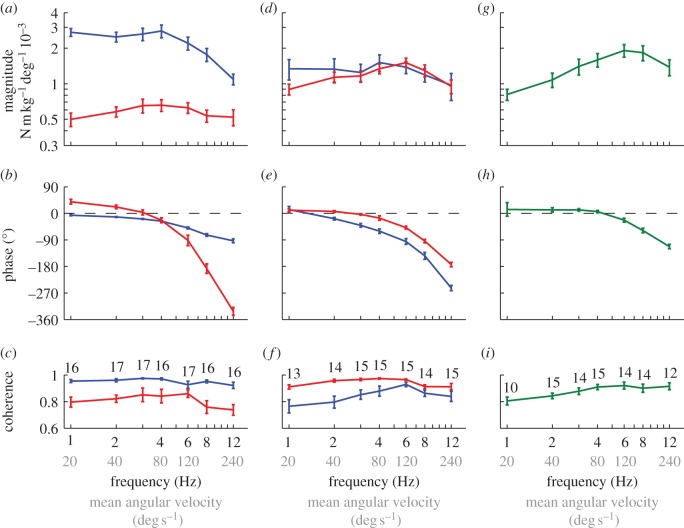
Measured responses to the stimulus set varying temporal frequency. Data points show means of the individual means ± 1 s.e. Blue, roll moment; red, yaw moment; green, pitch moment. (a–c) Response to roll stimuli. (d–f) Response to yaw stimuli. (g–i) Response to pitch stimuli. (a,d,g) Magnitude of the response relative to the angular position of the stimulus. (b,e,h) Phase of the response relative to the angle of the stimulus. (c,f,i) Coherence of the response. The numbers by each point indicate the number of moths that responded to that stimulus.

Figure 4.

Orientation of the mean major axis of the response to roll and yaw stimuli in the stimulus set varying temporal frequency. (a–c) Roll and yaw moments plotted against each other for 1, 4 and 8 Hz roll stimuli, respectively. (d–f) Roll and yaw moments plotted against each other for 1, 4 and 8 Hz yaw stimuli, respectively. The elliptical orbits represent the path traced by the tip of the total moment vector, where the direction of the vector defines the axis about which the moment is produced and where the length of the vector represents the magnitude of the total moment. The dashed magenta line indicates the major axis of the ellipse, which we take to define the major axis of the response. If the roll and yaw components of the response are in phase, then the ellipse collapses to a straight line. The grey-shaded circles correspond to the stimulus phases marked in the inset. The outline of the moth's body is shown to illustrate the direction of the major axis of the response relative to the moth's body axes.

The moths responded to yaw stimuli by producing roll and yaw moments of similar magnitude but varying relative phase (figure 3d). The small accompanying pitch moments had low coherence, so were not attributable to the yaw stimulus. The moments produced in response to a 1 Hz yaw stimulus were almost exactly in phase, but the roll moment lagged the yaw moment increasingly at higher stimulus frequencies (figure 3e). Consequently, the total moment vector swept a broad elliptical path through the course of each yaw stimulus cycle at stimulus frequencies greater than 1 Hz (figure 4d–f). The major axis of this ellipse, which we take to define the major axis of the moths’ response to yaw stimuli, was intermediate between the roll and yaw axes at all frequencies, and was approximately perpendicular to the long body axis.

The moths responded to pitch stimuli by producing large pitch moments of the appropriate sense to counteract their apparent self-motion (figure 3g). The small accompanying roll and yaw moments had low coherence, so were not attributable to the pitch stimulus. This is to be expected, because any other result would imply a lateral asymmetry in the response to symmetric motion in the left and right visual hemispheres.

3.2. Temporal frequency dependency of the measured responses

As explained earlier (see §2.6), our plots of response magnitude and phase against stimulus temporal frequency should not be treated as linear frequency responses, because the response of the system that they describe depends upon the amplitude as well as the temporal frequency of the stimulus. Nevertheless, for a given stimulus amplitude, the plots can still be used to identify the motion properties of the stimulus to which the moth is responding. For example, because we define the stimulus by its angular position, a flat magnitude response with zero phase would imply a proportional response to the angular position of the stimulus. At the other extreme, a response with a 90° phase lead whose magnitude increased linearly with frequency would indicate a proportional response to the angular velocity of the stimulus. This is because the angular velocity of the stimulus leads its angular position by 90°, and itself increases linearly with frequency. A mixed proportional response to the angular position and angular velocity of the stimulus would display a combination of these characteristics, with a linearly increasing magnitude response and an increasing phase lead less than 90°. These are idealized cases, and in practice, we would expect the measured responses to reflect the effects of nonlinearities, time delays and filtering. For example, the presence of a constant time delay would be expected to cause a phase lag that increased linearly with stimulus frequency.

It is important to note that a moth could, in principle, respond to the angular position of a stimulus either by detecting the angular position of the stimulus directly, or by detecting the angular velocity of the stimulus and integrating to estimate its position. These possibilities are not mutually exclusive, so in stating that a moth responds proportionally to the angular position of the stimulus, we neither imply that, nor exclude the possibility that, the moth detects the angular position of the stimulus directly. When describing the measured responses, we place particular emphasis upon whether the response leads or lags the angular position of the stimulus at the lowest stimulus frequency, and interpret the other properties of the response in the light of this. This is because the presence of a phase lead in a causal system is sufficient to demonstrate that the system is responsive to the derivative of its input. We use circular statistics to compute a 95% confidence interval for the response phase, under the assumption that the phase data follow a Von Mises distribution at a given stimulus frequency [35]. This approach avoids the need to make the more detailed assumptions about the system that would be necessary to enable formal system identification.

The roll component of the moths’ response to roll stimuli of varying temporal frequency had a small but statistically significant phase lag at a stimulus frequency of 1 Hz (circular mean: –6.4°; circular 95% confidence interval: –10.8, –2.0°), but no statistically significant variation in response magnitude up to a stimulus frequency of 4 Hz (figure 3a,b). Because the magnitude of the response is referenced to the angular position of the visual stimulus, this implies that the moths produced roll moments approximately in proportion to the angular position of the roll stimulus when the visual field was rolling slowly, albeit with a small lag. The phase lag increased linearly with increasing stimulus frequency from 1 to 4 Hz (figure 3b), which would be expected if there were a constant time delay in the system, because the same time delay constitutes a linearly increasing proportion of the stimulus period with increasing stimulus frequency. The response phase rolled off at a rate of –6.7° s between 1 and 4 Hz (regression slope of circular mean response phase on stimulus frequency), which would indicate a fixed time delay of 19 ms assuming that this were the only cause of the roll-off at low stimulus frequencies. A processing delay is expected to be present in any neural system, and delays longer than 10 ms are typical where visual processing is involved, so this result seems reasonable. Both response magnitude and phase decreased sharply at stimulus frequencies above 4 Hz, which cannot be explained by the presence of a fixed time delay, but could be caused by low-pass filtering and/or nonlinearities in the visual system's response to stimuli of increasing angular velocity. The yaw component of the moths’ response to roll stimuli of varying temporal frequency was much smaller in magnitude (figure 3a). However, the large phase lead at a stimulus frequency of 1 Hz (circular mean: 39.4°; circular 95% confidence interval: 17.3, 61.4°) and the apparent increase in response magnitude up to a stimulus frequency of 4 Hz (figure 3b) together indicate that the moths were responsive to the angular velocity, as well as angular position, of the stimulus.

The yaw component of the moths’ response to yaw stimuli of varying temporal frequency had a small but statistically significant phase lead at a stimulus frequency of 1 Hz (circular mean: 11.0°; circular 95% confidence interval: 1.8, 20.3°), which rolled off increasingly steeply with increasing stimulus frequency (figure 3e). The magnitude of the response increased up to a stimulus frequency of 6 Hz, but decreased sharply at higher frequencies (figure 3d). The statistically significant phase lead and increasing response magnitude at low-stimulus frequencies both indicate that the moths were responsive to the angular velocity of the stimulus, but the small size of the phase lead and the shallow slope of the response magnitude implies that the angular position of the stimulus was weighted much more heavily in the response. The sharply declining magnitude and phase of the response at higher frequencies could be due to low-pass filtering and/or nonlinearities in the system's response to stimuli of increasing angular velocity. The roll component of the moths’ response to yaw stimuli of varying temporal frequency (figure 3d,e) was qualitatively similar to the roll component of their response to roll stimuli (blue lines in figure 3a,b), but had a flatter magnitude response and a much faster roll-off in phase at stimulus frequencies from 1 to 4 Hz. The apparent phase lead observed at a stimulus frequency of 1 Hz was not statistically significant (circular mean: 12.8°; circular 95% confidence interval: –10.8, 36.4°), so we refrain from drawing any definite conclusions about the motion properties of the yaw stimulus to which the moths were responding when producing roll moments.

The moths’ response to pitch stimuli of varying temporal frequency had a small apparent phase lead at a stimulus frequency of 1 Hz, but this was not statistically significant (circular mean: 13.3°; circular 95% confidence interval: –67.2, 93.9°) owing to an unusually high degree of variability in the phase of the responses to the individual presentations of this stimulus. Moreover, 11 of these 29 individual stimulus presentations had coherence less than 0.6 and were therefore excluded from the analysis. This is an unusually high rate of exclusion, with odds of 10 : 1 that a measured response had coherence less than 0.6 for a pitch stimulus at 1 Hz, when compared with all other stimulus conditions. We therefore conclude that the moths did not respond consistently to pitch stimuli at 1 Hz. However, the phase response was almost flat across stimulus frequencies from 2 to 4 Hz, and had a statistically significant phase lead (pooled circular mean: 9.8°; pooled circular 95% confidence interval: 3.2, 16.4°). The response to pitch stimuli also showed a definite increase in magnitude up to a stimulus frequency of 6 Hz. Taken together, these features of the response indicate that the moths were responsive to both the angular position and angular velocity of the stimulus. However, given that the response to pitch stimuli had only a small phase lead at low frequencies (figure 3h), the angular position of the stimulus appears to be weighted much more heavily in the response. The sharp decrease in the magnitude and phase of the response at stimulus frequencies above 6 Hz could again be due to low-pass filtering and/or nonlinearities in the system's response to increasing angular velocity.

3.3. Contrast frequency dependency of the measured responses

The magnitude and phase response of a linear system depends only upon the temporal frequency of its input. Consequently, any effect of oscillation amplitude or spatial frequency would be clear evidence of nonlinearity in the measured responses. Of course, any real physical system is expected to saturate eventually, so the important question is whether there is evidence for nonlinearity within its useful working range (i.e. before the system saturates).

The roll moments that the moths produced in response to roll stimuli of varying amplitude increased with increasing oscillation amplitude up to a stimulus amplitude of 20°, but saturated beyond this point (figure 5a). The magnitude of the response decreased with increasing oscillation amplitude over the entire range of stimulus amplitudes that we presented, before decreasing sharply at the point of saturation (figure 5b). The phase of the response also varied with oscillation amplitude, advancing in phase up to a stimulus amplitude of 20° (figure 5c). These results demonstrate nonlinearity over the entire range of stimulus amplitudes that we presented. Hence, as the system only shows signs of saturating at the highest stimulus amplitudes, we conclude that the optomotor system is nonlinear within its useful working range.

Figure 5.

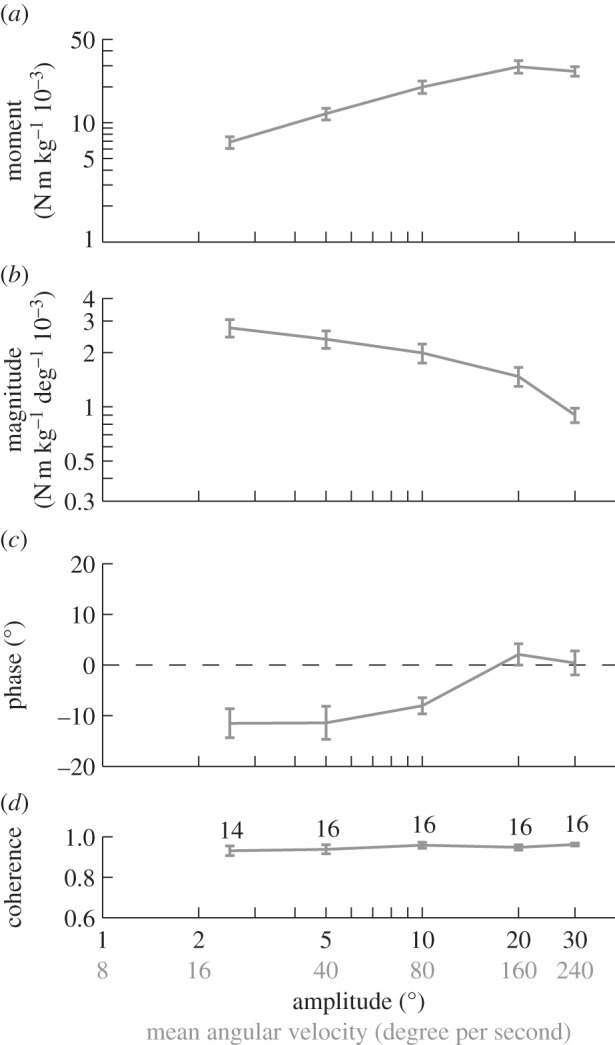
Roll moment response to the stimulus set varying oscillation amplitude. Data points show means of the individual means ± 1 s.e. (a) Roll moment normalized by body mass. (b) Magnitude of the roll moment relative to the angular position of the stimulus. (c) Phase of the response relative to the angle of the stimulus. (d) Coherence of the response. The numbers by each point indicate the number of moths that responded to that stimulus.

When presented with roll stimuli of varying spatial frequency, no moth responded coherently to stimuli at the highest spatial frequency of 0.333 cycles per degree, which suggests that the visual system may be unable to resolve a sinusoidal grating with a wavelength of 3°. The moths responded with high coherence at lower spatial frequencies, and their response phase advanced with increasing spatial frequency (figure 6b). The magnitude of the moths’ response did not vary significantly with spatial frequency between 0.025 and 0.050 cycles per degree, but decreased with increasing spatial frequency from 0.050 to 0.167 cycles per degree (figure 6a). Once again, this provides clear evidence that the response properties of the optomotor system are nonlinear within its useful working range.

Figure 6.

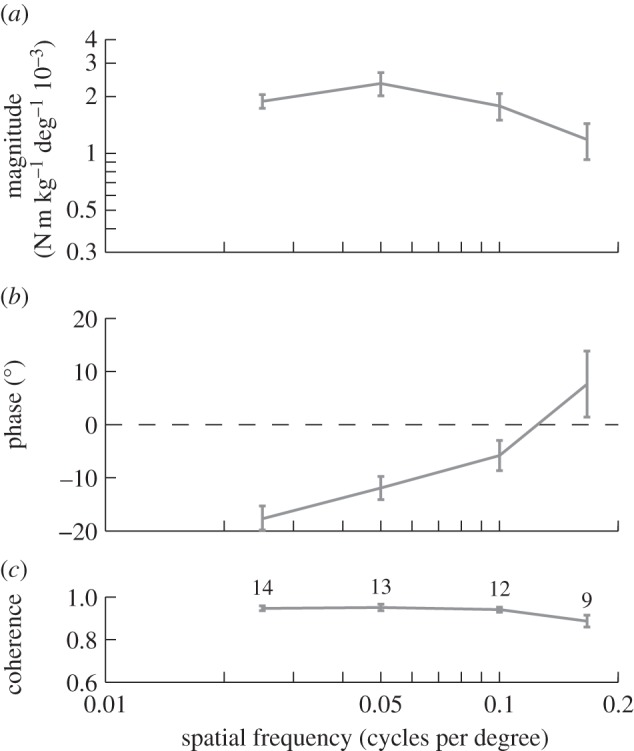
Roll moment response to the stimulus set varying spatial frequency. Data points show means of the individual means ± 1 s.e. (a) Magnitude of the roll moment relative to the angular position of the stimulus. (b) Phase of the response relative to the angle of the stimulus. (c) Coherence of the response. The numbers by each point indicate the number of moths that responded to that stimulus. No moth responded coherently to the stimulus with 0.333 cycles per degree spatial frequency.

We would expect to see evidence of such nonlinearity in any optomotor system based upon correlation-type motion detectors, because the response of such detectors depends nonlinearly upon contrast frequency [28]. The mean contrast frequency of the stimuli that we provided would have been proportional to the amplitude of oscillation, the spatial frequency of the grating and the temporal frequency of the oscillation. Hence, if the system's response depended only upon contrast frequency, then increasing the spatial frequency of the grating, while keeping the temporal frequency constant, would be expected to have precisely the same effect as increasing the oscillation amplitude by the same degree. Figure 7 compares the magnitude and phase of the measured responses to roll stimuli of varying oscillation amplitude and spatial frequency as a function of contrast frequency, and shows that the measured responses are essentially indistinguishable when presented in this way. Of course, the spatial frequency of the stimulus also has an effect independent of contrast frequency at the highest spatial frequencies, where the visual system appears to be unable to resolve the grating.

Figure 7.

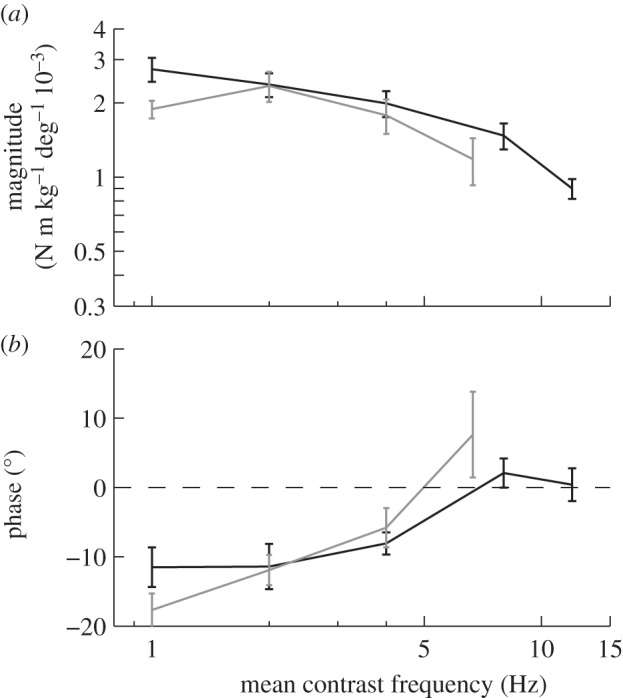
Roll moment response to the stimulus sets varying spatial frequency (grey lines) and oscillation amplitude (black lines), plotted as a function of contrast frequency. Data points show means of the individual means ± 1 s.e. (a) Magnitude of the roll moment relative to the angular position of the stimulus. (b) Phase of the response relative to the angle of the stimulus.

4. Flight dynamics analysis

4.1. Theoretical flight dynamics model

We used a previously published linear time-invariant model of hawkmoth flight dynamics [23–25] to predict the unstable motions that the measured optomotor responses might be expected to stabilize. This model was originally fitted for the larger species Manduca sexta (L.) [23–25], so we rescaled its parameters to take account of the smaller body mass, moments of inertia and wing area of our study species H. lineata (for details, see the electronic supplementary material). The original model [23–25] was derived from the Newton–Euler equations of rigid-body motion, and was parametrized using a computational fluid dynamics model to simulate the aerodynamic forces and moments during small perturbations from an equilibrium state of hover. Those simulations were used to fit the wingbeat-averaged forces and moments as linear functions of the insect's velocity and angular velocity, and the slopes of the fitted functions were then treated as estimating the partial derivatives of the forces and moments with respect to the motion state variables, and used to parametrize the system matrix. Because the aerodynamic forces and moments were originally simulated during disturbances corresponding to angular velocities within the range ±360° s^–1, the results from the rescaled flight dynamics model should not be extrapolated outside of this range.

The flight dynamics model is of the general form:

4.1

where t is time, A is a system matrix with time-invariant entries given in the electronic supplementary material and x(t) is the state vector. For a bilaterally symmetric system, the linearized equations of motion that describe the lateral and longitudinal flight dynamics are decoupled and can therefore be treated separately. For longitudinal motions, the state vector x(t) = [δu, δw, δq, δθ]^T represents small disturbances from equilibrium in forward velocity (u), dorsoventral velocity (w), pitch rate (q) and pitch angle (θ). For lateral motions, the state vector x(t) = [δv, δp, δr, δγ]^T represents small disturbances from equilibrium in sideslip velocity (v), roll rate (p), yaw rate (r) and roll angle (γ). Solutions to equation (4.1) are characterized by the eigenvalues (tables 2 and 3) and eigenvectors (tables 4 and 5) of the longitudinal or lateral system matrix (see also the electronic supplementary material).

Table 4.

Eigenvectors characterizing the longitudinal natural modes of motion of H. lineata predicted by the theoretical flight dynamics model.

	slow, unstable oscillatory mode		fast, stable monotonic mode		slow, stable monotonic mode
	magnitude	phase (°)	magnitude	phase (°)	magnitude	phase (°)
δu	0.52	123	0.52	0	7.65	0
δw	0.01	235	0.01	0	71.77	180
δq	18.11	65	19.92	180	2.37	180
δθ	1	0	1	0	1	0

Table 5.

Eigenvectors characterizing the lateral natural modes of motion of H. lineata predicted by the theoretical flight dynamics model.

	slow, unstable monotonic mode		stable oscillatory mode		fast, stable monotonic mode
	magnitude	phase (°)	magnitude	phase (°)	magnitude	phase (°)
δv	0.85	0	0.72	220	0.15	180
δp	7.88	0	16.79	147	84.38	180
δr	0.10	0	1.16	122	102.53	0
δγ	1	0	1	0	1	0

As a rule of thumb, it is reasonable to use a time-invariant model to approximate the body dynamics if the forcing frequency of the wingbeat is at least an order of magnitude higher than the highest natural frequency of the flight dynamics [36]. The flight dynamics model predicts longitudinal and lateral oscillatory modes of motion with periods of 16 and 28 wingbeats, respectively (tables 2 and 3). We would therefore expect from first principles that the wingbeat-averaged model should offer a reasonable first approximation to the lateral and longitudinal flight dynamics of H. lineata. The validity of the flight dynamics model was previously verified for M. sexta by comparing its analytical predictions with the results of simulations coupling the rigid-body equations of motion with the Navier–Stokes equations [24,25]. These simulations match the analytical results of the model quantitatively for the longitudinal flight dynamics [24], but only qualitatively for the lateral flight dynamics [25]. However, as the separation of timescales between the rigid-body flight dynamics and the wingbeat is predicted to be greater in H. lineata than in M. sexta, we would expect the rescaled flight dynamics model to perform no worse than the published flight dynamics model in this respect, and perhaps rather better.

The flight dynamics model predicts the existence of three longitudinal modes of motion in H. lineata: a slow, unstable oscillatory mode; a fast, stable monotonic mode; and a slow, stable monotonic mode (table 2). Exactly the same modal structure has been identified by every model of the natural longitudinal flight dynamics of hovering insects that has been published to date [23,24,37–44]. Furthermore, the unstable oscillatory mode has been found to involve coupled oscillations in fore–aft velocity and pitch in every case (see also table 4). We therefore have a high degree of confidence that the flight dynamics model correctly predicts the nature of the unstable longitudinal motions that the optomotor responses of H. lineata might be expected to stabilize. The flight dynamics model also predicts the existence of three lateral modes of motion: a slow, unstable monotonic mode; a fast, stable monotonic mode; and a stable oscillatory mode of intermediate timescale (table 3). The same modal structure has been identified by several other models of the natural lateral flight dynamics of hovering insects [25,44–46], but some simpler models of the lateral flight dynamics predict that the first monotonic mode is stable [41,47]. This discrepancy is attributable to an aerodynamic instability that is not captured by the simpler models [46]. We are therefore confident that the flight dynamics model correctly predicts the nature of the unstable lateral motions that the optomotor responses of H. lineata might be expected to stabilize.

4.2. Function of the measured optomotor responses in flight stabilization

The theoretical flight dynamics model predicts the existence of two unstable modes of motion that would have to be stabilized in the real insect through feedback control (see tables 2 and 3). One of these is a lateral motion involving a slow, monotonic divergence in roll rate and sideslip (figure 8a; see also table 5). Sideslip velocity (in ms^–1) is predicted to be approximately 0.1 times roll rate (in rad s^–1) in this roll divergence mode, which describes tangential motion along an arc of radius 0.1 m (i.e. approx. three body lengths). The same instability has been predicted by several models of the natural flight dynamics of hovering insects, so is expected to be a common feature of insect flight [25,44–46]. The second unstable mode is a longitudinal motion involving coupled oscillations in fore–aft velocity and pitch (figure 8c; see also table 4), and resembles the phugoid mode of a hovering helicopter [48]. The same longitudinal instability has been predicted by every other model of the longitudinal flight dynamics of hovering insects yet published, so is expected to be a general feature of insect flight [23,24,37–44]. Both unstable modes of motion are predicted to take approximately four wingbeats (0.1 s) to double in magnitude (see tables 2 and 3), so we would expect the insect to have sufficient time to observe their excitation, and to respond accordingly. Testing quantitatively whether the moths’ optomotor response is sufficient to stabilize their flight dynamics would require a more detailed model of the optomotor response than we have available, but an obvious question to ask is whether any of the optomotor responses that we have measured could, in principle, contribute to their stabilization?

Figure 8.

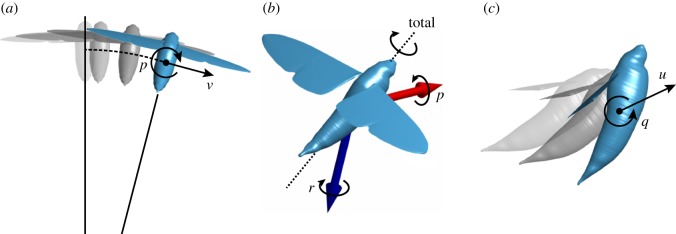
Diagrams illustrating three of the natural modes of motion that the theoretical flight dynamics model predicts. Animations accompany each of these figures as movies S1–S3 in the electronic supplementary material. (a) The roll divergence mode involves a slow, monotonic divergence in roll rate (p) and sideslip (v). In this mode, the moth's centre of mass effectively moves with increasing angular velocity along an arc of radius 0.1 m (dashed line). (b) The fast subsidence mode involves a fast, monotonic subsidence in roll and yaw. In this mode, roll rate (p) and yaw rate (r) have similar magnitude but opposite sign, so the mode involves heavily damped rotation about an axis close to the body's long axis (dashed line). (c) The unstable phugoid mode involves coupled oscillations in fore–aft velocity (u) and pitch rate (q). The grey outlines represent past states of the moth.

The roll divergence mode can be controlled through the application of a pure moment, and this is most effective if the moment is applied about an axis pitched 3° below the nominal roll axis (for details, see electronic supplementary material). Turning moments applied about this optimal axis must be commanded using roll angle feedback in order to provide stability: feeding back sideslip velocity or roll rate alone is insufficient to stabilize the roll divergence mode, and feeding back roll rate in addition to roll angle only serves to reduce the damping (figure 10a; for methods, see the electronic supplementary material). These qualitative conclusions are robust to assuming a constant time delay of as much as two wingbeats, and we therefore predict that any response involved in stabilizing the roll divergence mode should involve feeding back roll angle to roll moment. Consistent with this prediction, the roll moments that the moths produced in response to roll stimuli of varying temporal frequency were approximately proportional to roll angle at low-stimulus frequencies, with evidence of a time delay of less than one wingbeat (see §3.2). Furthermore, the direction of the major axis of the moths’ response to roll stimuli was close to the optimal axis for controlling the roll divergence mode (figure 9a). The moths’ measured optomotor response to roll stimuli therefore coincides with what we would expect to see in a response functioning to stabilize the predicted roll divergence mode.

Figure 10.

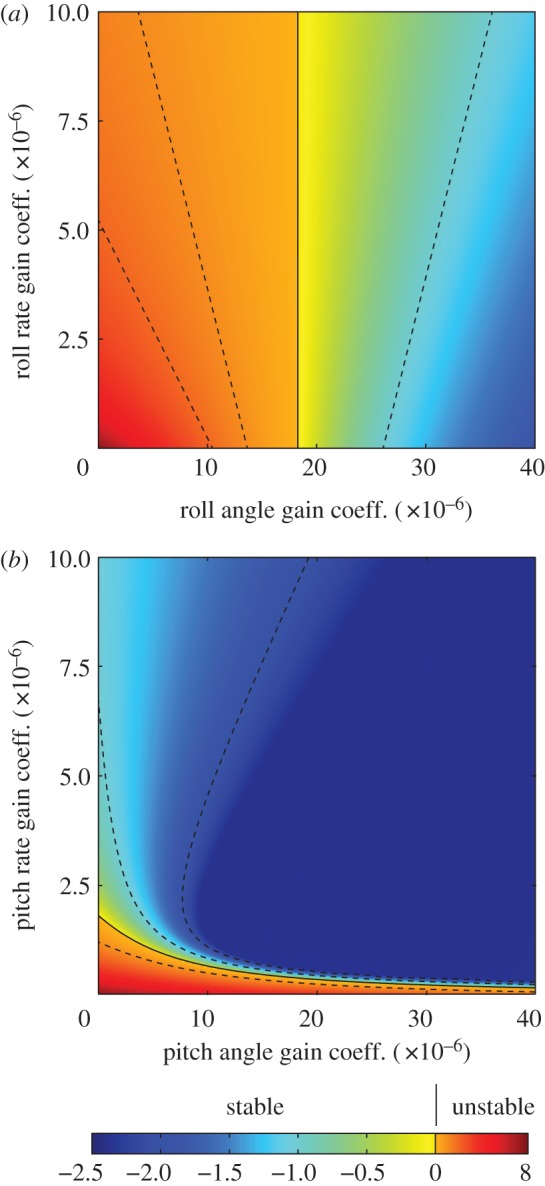
Eigenvalue plots showing how feedback control is predicted to affect the stability of the two modes of motion requiring active stabilization. (a) Closed-loop stability of the roll divergence mode, assuming proportional feedback of roll angle and/or roll rate to command a moment offset 3° below the roll axis. Moments applied about this axis contribute maximum energy to this mode, and therefore best control it. (b) Closed-loop stability of the unstable phugoid mode, assuming proportional feedback of pitch angle and/or pitch rate to command a moment about the pitch axis. The colour of the plot represents the real part of the corresponding eigenvalue, where a positive real part indicates an unstable mode, and where a negative real part indicates a stable mode. Dashed lines are contour lines, and the solid contour indicates the threshold between stability and instability. Note the difference in the scale of the colour bar for positive (i.e. unstable) and negative (i.e. stable) eigenvalues. See the electronic supplementary material for explanation of the gain coefficients.

Figure 9.

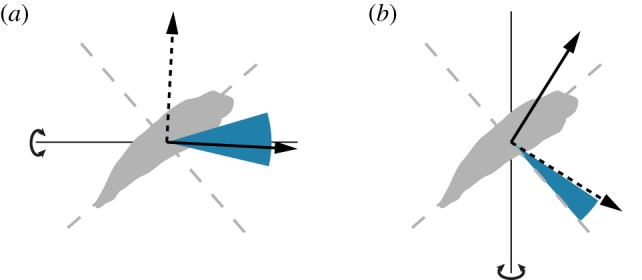
Directions of the major axes of the moths’ response to roll and yaw stimuli, compared with the direction of the moment that is predicted to transfer maximum or minimum energy into a given mode of motion. The stimulus axis is shown as a thin black line with a curved arrow, and the range of the major axes of the responses across all stimulus frequencies is shown by the blue-shaded wedge. The principal axes of inertia of the moth are marked with dashed grey lines. The axes about which applied moments would theoretically contribute maximum or minimum energy to a given natural mode of motion are indicated with solid and dashed black vectors, respectively. (a) Variation in the major axis of the measured response to roll stimuli compared with the direction of the moment that transfers maximum or minimum energy into the roll divergence mode. (b) Variation in the major axis of the measured response to yaw stimuli compared with the direction of the moment that transfers maximum or minimum energy into the fast subsidence mode.

The unstable phugoid mode can also be controlled through the application of a pure moment, which of course should be applied about the pitch axis. This mode can be stabilized by feeding back either pitch angle or pitch rate to command pitch moment, but stability is enhanced by feeding back pitch angle and pitch rate together (figure 10b; for methods, see the electronic supplementary material). These qualitative conclusions are robust to the assumption of a time delay of up to 1.75 wingbeats. Several modelling studies have also shown that a combination of pitch angle and pitch rate feedback could be used to stabilize the unstable phugoid mode of hovering insects [38,40,49]. We therefore predict that any response involved in stabilizing the longitudinal oscillatory mode should involve feeding back a mixture of pitch angle and pitch rate to control pitch moment. In accordance with this prediction, our moths responded to pitch stimuli of varying temporal frequency by producing an opposing pitch moment that approximated a mixed response to pitch angle and pitch rate. The phase of the moths’ response to pitch stimuli was inconsistent at a stimulus frequency of 1 Hz (figure 3h), but was consistent at higher stimulus frequencies, and was especially consistent at the 3 Hz stimulus frequency, which coincides most closely with the predicted frequency of the unstable phugoid mode (table 2). The moths’ measured optomotor response to pitch stimuli therefore coincides with what we would expect to see in a response functioning to stabilize the predicted unstable phugoid mode.

4.3. Function of the measured optomotor responses in control of heading

In addition to the two unstable modes of motion, the theoretical flight dynamics model also predicts the existence of four stable modes of motion in the natural flight dynamics (tables 2 and 3). Motions that are naturally stable do not require stabilization through feedback control, but they are important nonetheless, because their damping makes it energetically more costly to move about some axes than others. The most heavily damped of the four stable modes is a lateral motion involving a fast, monotonic subsidence in roll and yaw, which takes less than half a wingbeat (0.01 s) to halve in magnitude (table 3). This fast subsidence mode involves roll and yaw rates that are of similar magnitude but opposite sign (table 5). It therefore involves heavily damped motion about an axis close to the body's long axis, which is intermediate between the nominal roll and yaw axes in hover (figure 8b). A fast subsidence mode involving a highly damped rotation about an axis close to the body's long axis has been predicted by several models of the natural flight dynamics of hovering insects [25,41,45,46], so is expected to be a common feature of insect flight.

Although the fast subsidence mode involves coupled roll and yaw motions, it is primarily attributable to the ‘flapping counter torque’ [50] that results when a pair of flapping wings is rotated about an axis normal to their stroke plane [41,45]. This axis is always close to the yaw axis in hovering flight, so to a first approximation, the fast subsidence mode is driven by yaw rate damping. Flapping counter torques have been discussed extensively in the context of yaw turns [18,50–52], but a moment applied about the yaw axis will only produce an angular acceleration about the yaw axis if the yaw axis is itself a principal axis of inertia. If the yaw axis is not a principal axis, which it will not be if the long body axis is tilted with respect to the horizontal at equilibrium, then an applied yaw moment will couple into roll—an effect known as inertial coupling (see §5.2 and electronic supplementary material).

The natural flight dynamics of an insect are unaffected by its heading, so although yaw motions are expected to be heavily damped, the natural flight dynamics have no tendency to correct deviations in heading. We therefore hypothesize that the optomotor response to yaw stimuli serves to control heading. Control inputs that inject energy into the fast subsidence mode are expected to be energetically costly because of its high damping. A natural question to ask, therefore, is whether the optomotor response to yaw stimuli injects much energy into this mode. The major axis of the moths’ response to yaw stimuli was approximately normal to the body's long axis (figure 4e–f). Moments applied about this axis transfer comparatively little energy into rotations about the body's long axis, by virtue of being applied almost orthogonal to it. Consequently, the measured response to yaw stimuli transfers comparatively little energy into the highly damped fast subsidence mode (figure 9b; for methods, see the electronic supplementary material). The directional properties of the measured optomotor response to yaw stimuli therefore make sense if its function is to control heading in an energetically efficient way.

5. Discussion

5.1. Nonlinearity of the measured responses

The contrast frequency dependency of the measured responses, and the decrease in response magnitude that we observed at very high image velocities, is consistent with the hypothesis that the insects sense their apparent self-motion using correlation-type motion detectors [28]. The output of a correlation-type motion detector is approximately proportional to the angular velocity of local image motion over a certain range of stimulus parameters, but depends fundamentally upon the contrast frequency of the visual stimulus. The detector's response to contrast frequency is highly nonlinear, increasing to a maximum with increasing contrast frequency, but decreasing to zero at higher contrast frequencies. It has been suggested that these nonlinearities help to keep the optomotor control system stable [53], despite the substantial time delays inherent in visual processing. This being so, it is significant that our measurements of the moths’ optomotor responses appear to capture the effects of these nonlinearities. A quantitative analysis of the extent to which the properties of the visual system can explain the properties of the moths’ optomotor response will be provided elsewhere, together with an analysis of the role of head movements in flight stabilization and control.

5.2. Inertial coupling of roll and yaw

Our moths produced coupled roll and yaw moments in response to yaw stimuli. This makes sense in the light of the fact that the flight dynamics model predicts strong inertial coupling between roll and yaw (see also §4.3). This inertial coupling of angular acceleration in roll and yaw is completely distinct from the mechanical coupling of roll angle and yaw rate that characterizes banked turns, and is expected to be a general feature of hovering flight in insects. This is because the roll and yaw axes of a hovering insect are conventionally defined as those axes within the insect's plane of symmetry that are horizontal and vertical, respectively, at equilibrium. Because most insects hover with their long body axis tilted with respect to the horizontal, it follows that the roll and yaw axes will not be principal axes of inertia. Consequently, there is expected to be significant coupling of angular acceleration about the roll and yaw axes, and it is therefore most unlikely that the flight dynamics can be separated into orthogonal roll and yaw motions as conveniently as they can be for an aircraft, in which the longitudinal axis is horizontal at equilibrium.

The inertial coupling of roll and yaw has important implications for studies of insect flight control. For example, almost every optomotor response study that has recorded the moments produced by tethered insects to date has done so using a single-axis torque meter aligned with the axis of the rotational visual stimulus (see [21] for review). Such studies are likely to have missed important components of the optomotor response—especially in respect of yaw stimuli, which we have shown elicit roll and yaw moments of similar magnitude in hawkmoths. In a similar vein, several recent studies of turning flight have treated free-flying insects as if they were constrained to rotate about only the yaw axis [18,50–52,54]. This treatment makes sense only if the yaw axis is a principal axis of the body, and does not fully account for the insect's inertial properties if it is not.

5.3. Wider implications

Our results show how the physiological responses of insects can be related to the physics of their natural flight dynamics. We have shown by example how a theoretical flight dynamics model can be used to make detailed predictions about the natural flight dynamics of an insect. The model predicts the existence of two unstable modes of motion in the flight dynamics of the uncontrolled system, so if the same instabilities are present in the natural flight dynamics of the real insect, then they must necessarily be stabilized through feedback control. The model predicts that roll angle feedback without roll rate feedback is appropriate to stabilize the lateral flight dynamics through the application of a roll moment, but that a combination of pitch angle and pitch rate feedback will be most effective in stabilizing the longitudinal flight dynamics through the application of a pitch moment. The optomotor responses that we have measured involve feeding back roll angle to roll moment, and feeding back pitch angle and pitch rate to pitch moment. The measured optomotor responses therefore coincide qualitatively with the control responses that we would expect to see in a control system functioning to stabilize the unstable modes of motion whose existence is predicted by the theoretical flight dynamics model. Furthermore, the response properties that we have measured match qualitatively those that would be expected given the known properties of the interneurons that are responsible for processing motion vision. Our conclusions are therefore consistent with the broader hypothesis that the sensorimotor systems of insects are matched directly to the modes of motion that they control [22]. Future work will test this mode-sensing hypothesis directly by designing the visual stimuli that we present to coincide with the non-orthogonal directions that we predict are most relevant to the flight dynamics.

Funding statement

The research leading to these results has received funding from the European Research Council under the European Community's Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 204513. The virtual-reality flight simulator was built under BBSRC Research grant no. BBC5185731. R.J.B. is supported by EPSRC Fellowship EP/H004025/1.