Abstract
Two types of measurement are presented that relate molecular events to macroscopic behavior of F-actin networks. First, shear modulus is measured by oscillating an embedded microbead. Second, a microbead is translated at constant rate and transitions in the resisting force are observed. The loading rate dependence of the force at the transitions is similar to that of the molecular unbinding force, suggesting that they share a common origin. Reversibility tests of shear modulus provide further evidence that strain softening of F-actin networks is caused by force-induced rupture of cross-links.
Actin assembles into cross-linked networks of actin filaments (F-actin) that provide physical support for the cell and play important roles in numerous cellular processes. In vitro, reconstituted F-actin networks cross-linked with various actin binding proteins (ABPs) exhibit complex nonlinear mechanical behavior. At small strains, they exhibit frequency-dependent viscoelastic moduli [1]. At higher strains, the shear modulus first increases with applied strain, then softens as strain is further increased [2–5]. The elastic response of F-actin networks has been linked with the mechanical behaviors of F-actin [6] and is well characterized by the distance between cross-linking proteins [7]. When the network is subjected to external stress, stretching of the semiflexible F-actin induces network stress hardening [1, 4]. However, experiments also demonstrate that the properties of ABP are critical determinants of the dynamic behavior of the network under stress. The deletion of the hinge domain in filamin significantly alters the nonlinear behavior of a filamin/F-actin network [2]. Other experiments using various cross-linking agents demonstrate that the detailed molecular structure determines the critical stress for network softening [8]. Two properties of ABPs can cause stress relaxation at large strains: force-induced unbinding from the F-actin and sequential unfolding of internal domains. Sato et al. proposed molecular unbinding as a cause for the rapid rearrangement of the cytoplasm by examining the dependence of the mechanical properties of F-actin networks on deformation rate and temperature [9]. In recent studies, the unfolding of filamin have been well characterized by atomic force microscopy [10, 11], whereas optical trap measurements provided evidence of both unbinding and unfolding of a filamin cross-linking two F-actin over similar ranges of force [12]. Consequently, some uncertainty remains regarding the relative importance of unbinding and unfolding in the strain softening of F-actin networks.
In this letter, we prepare three F-actin gels: entangled F-actin solution, filamin/F-actin network and streptavidin/biotin-F-actin network, and measure the local, nonlinear shear moduli of those by relative oscillation of a 1 µm diameter polyethylene glycol-coated microbead within the matrix (see a protocol in the supplementary material [13]). We then present results from a second set of experiments in which a microbead is displaced linearly through the network while monitoring both the force level and displacement associated with sudden drops in force. By comparing the loading rate dependence of the transitions observed in the network responses with single molecule unbinding events, we suggest that network relaxation is due primarily to unbinding rather than unfolding of cross-linkers. Irreversible mechanical properties observed in the cross-linked F-actin network support the concept that network behavior is largely attributable to cross-link rupture.
To estimate the mechanical properties of F-actin gels, a microbead embedded in the gel is trapped by the optical tweezers and a sinusoidal excitation is imposed by oscillating the gel. The oscillation amplitudes are ±0.2–2.0 µm at a frequency of 10 Hz to apply controlled strains to the sample. The applied force (F) is calculated from the displacement of the microbead multiplied by the trap stiffness. Displacement relative to the network (x) is computed by subtracting the displacement of the microbead from that of the stage. We fit both the force and relative displacement to sinusoidal functions, and the shear moduli (G) are estimated from the equation,
| (1) |
where F̄ and x̄ are the amplitudes of F and x, respectively, and Δθ is the phase delay between F and x. G estimated at various amplitudes yield strain-dependent mechanical properties. G are normalized by their low-displacement values and displacements are normalized by the radius of the bead.
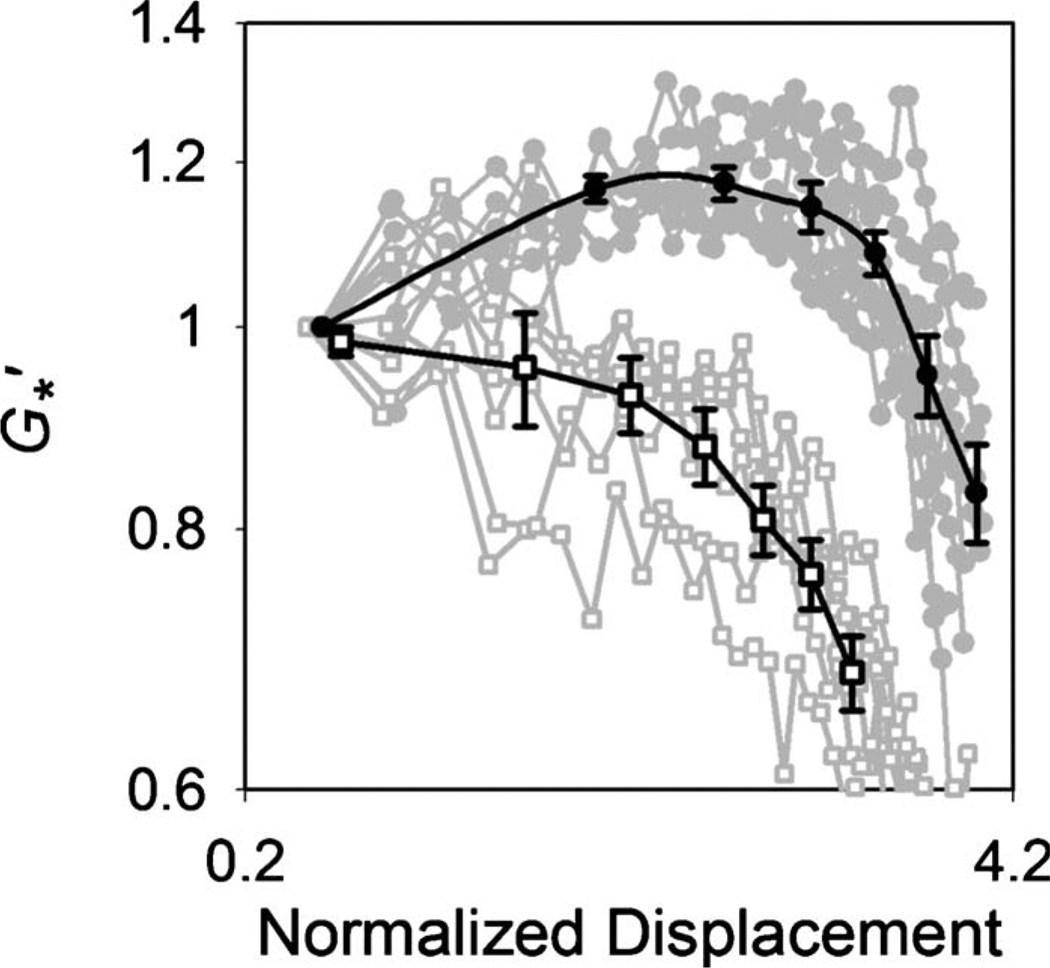
For the entangled F-actin solution to which no ABPs are added ([actin] cA=30 µM), the storage modulus (G′) monotonically decreases with increasing bead displacement [Fig. 1]. As there is no physical connection between actin filaments, they are displaced by the bead’s oscillation producing a lower local concentration of F-actin in the region. In contrast, the G′ of the cross-linked filamin/F-actin network (cA=30 µM, [filamin]/[actin] Rf=0.01) increases up to a critical level of bead displacement and then decreases suggestive of local collapse or softening of the network as large strain is applied. The network collapse occurs at approximately 20 pN. α-actinin/F-actin networks (cA=20 µM, Rα =0.01) exhibited amplitude-dependent mechanical properties similar in magnitude and shape to those of the filamin/F-actin networks (see Fig. S1 in the supplementary material [13]). This is likely due to the fact that ABPs have a conserved actin-binding domain exhibiting similar binding interactions with F-actin [14, 15]. The variations in G′ observed in these F-actin networks are qualitatively similar to those of F-actin networks under prestress probed at the macroscale [2, 16]. However, the increase in G′ in the strain-hardening region is considerably smaller in these experiments compared to the orders of magnitude difference observed in the macroscopic measurements. This inconsistency could be attributable to differences of measurement scale and force loading. In the macroscopic measurement, a small fraction of the network bears the bulk of the load while much of the rest is relatively relaxed. Excitation by an embedded bead, in our measurements, applies a highly localized stress with large strains close to the bead, falling off with distance. A complex strain field formed around the bead causes a large extension\compression\torsion on the actin filaments and cross-links close to the bead.
FIG. 1.
Normalized elastic modulus as a function of the normalized bead displacement. For the entangled F-actin solutions (□, n=6), monotonically decreases as bead displacement increases. For the filamin/F-actin networks (●, n=8), increases with bead displacement up to a critical value and then decreases. Black curves represent averages of gray curves.
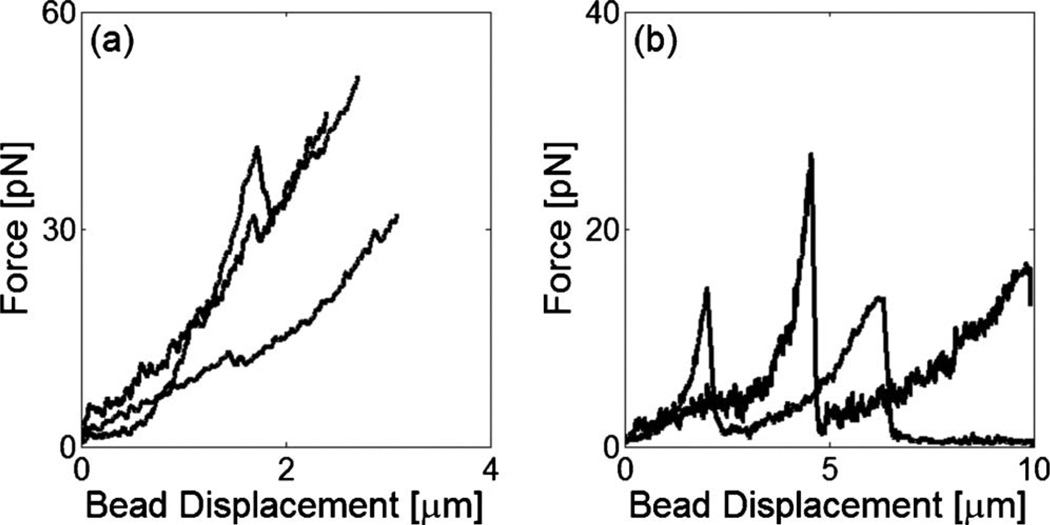
To elucidate the origin of the strain-hardening and strain-softening observed in the cross-linked F-actin networks, we obtain their mechanical responses to local, microscale forcing. An embedded microbead was captured by the fixed trap in space and the sample was displaced at a constant velocity of 5 µm/s using a piezocontrolled stage. For the filamin/F-actin network (cA=10 µM, Rf =0.01), the force-displacement traces exhibit single (61%) or multiple (39%) transitions at which the force does not drop to zero [Fig. 2(a)], suggestive of abrupt alterations in the network structure surrounding the bead. Similar force peaks were also observed in the rigidly cross-linked F-actin networks with streptavidin (see Fig. S2 in the supplementary material [13]). However, compared to the filamin/F-actin networks, they occurred at higher force with less probability implying that they were attributable to physical rearrangement of network structure or cross-link rupture. Transitions observed in the entangled F-actin solution (cA=10 µM) tended to exhibit larger displacement and lower force, and they generally relaxed to zero after the transitions, suggesting an event of a different kind [Fig. 2(b)]. The mechanical response of the F-actin solution should depend on local entanglement of F-actin. If the filaments are tightly entangled in the vicinity of the bead, they will be bent and accumulate in front of the bead during its displacement. Depending on the strength of entanglement, the F-actin can buckle with further bead displacement. The F-actin solutions polymerized at high-gelsolin concentrations ([gelsolin]/[actin]=1/100) did not exhibit force peaks, suggesting that F-actin entanglement plays a significant role in sustaining an external load. Alternatively, the microbead can slip through pores in the networks resulting in a transient reduction in force and a jump in displacement.
FIG. 2.
Representative force vs. displacement curves for cross-linked filamin/F-actin networks (a) and entangled F-actin solutions (b). Compared to the entangled F-actin solutions, the filamin/F-actin networks exhibit multiple transitions where the force does not relax to zero.
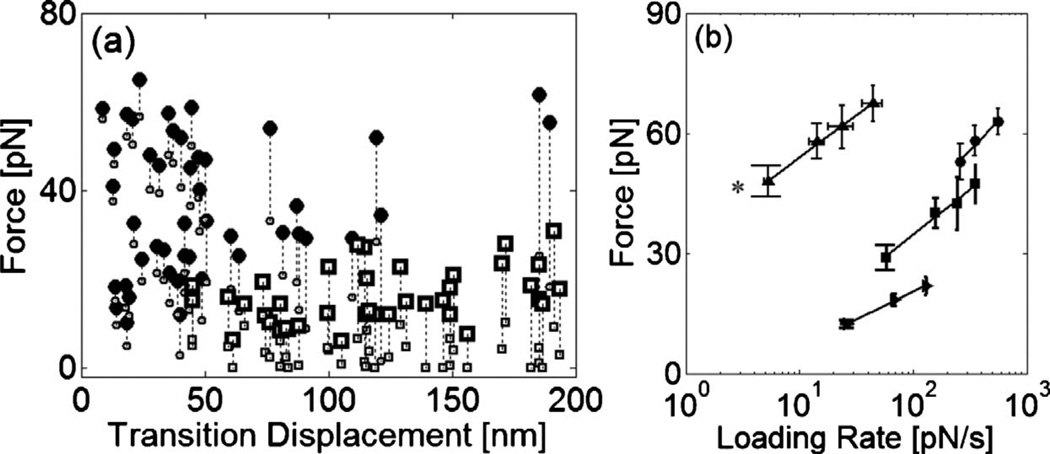
To further identify the cause of the transitions in the mechanical responses of the F-actin gels, we characterize the critical force and bead displacement at transition. Transition displacement measures a corresponding movement of the microbead at the force drop. Mean displacements at transition are 29±17 nm for the filamin/F-actin network, and 117±49 nm for the entangled F-actin solution [Fig. 3]. Transitions occur at 37±17 pN and 21±6.1 pN for the filamin/F-actin network and entangled F-actin solution, respectively. Compared to the F-actin solution, multiple transitions with smaller displacements were observed in the cross-linked F-actin network implying that abrupt decreases of force might result from force-induced rupture at cross-links or unfolding of cross-linking proteins. Unfolding of individual subdomains increases the contour length of filamin by ≈30 nm [11], which is similar to the average transition displacement in our measurements. Multiple transitions exhibited in Fig. 2(a) are also similar to the typical unbinding and unfolding traces exhibited in the direct pulling of ABP [10, 11, 17, 18].
FIG. 3.
(a) Relation of force and displacement at the transitions exhibited in the responses of the F-actin gels to linear bead displacement. For the filamin/F-actin network (●), the transitions occur at a force of 37±17 pN with a displacement of 29±17 nm. In contrast, for the entangled F-actin solution (□), they are observed at a lower force of 21±6.1 pN with larger displacement, 117±49 nm. Small symbols indicate forces after transition. (b) Dependence of transition force on loading rate for the F-actin solution (►), filamin/F-actin network (■), streptavidin/biotin-F-actin network (●). Rupture forces for actin gels increases as the loading rates increase. As the strength of cross-linker increases, the network rupture is observed at the higher force. Forces at the transitions observed in the filamin/F-actin networks’ responses exhibit a similar loading rate dependence of slope to unbinding force (▲) between a single filamin and F-actin. (*Results adapted from Ref. [12])
We also calculate the loading rate from the slope of a linear fit to the force versus time plot for each event. Compared to the previous measurements of loading-rate dependent bond strength [19], range of our loading rate is smaller being limited by the experimental constraints such as stage speed and data acquisition rate. The critical force scales as the logarithm of loading rate with a slope of 9.9, similar to the loading rate dependence of the molecular unbinding force between filamin and F-actin of 9.1 [Fig. 3(b)]. By comparison, the slope for non-cross-linked actin was 6.1. Differences in force magnitude are likely attributable to the fact that multiple bonds are loaded at varying distances from the bead and various types of forces are applied to the bonds in the network experiment. Since force on a bead is sustained through multiple cross-links, the probability that one of them will rupture is higher at a given level of force and the weakest of the populations will be probed in our measurement. Also, when a force is applied by a microbead, cross-links in the network undergo force at various angle. As unbinding force decreases significantly as pulling angle increases [20], a bond subject to angular torque should rupture at lower force. Despite these differences, the response of the F-actin network to a local excitation exhibits similarities in the trace pattern, the critical force for transition, and the loading rate dependence, compared with the molecular unbinding trace of a single filamin and F-actin complex [12].
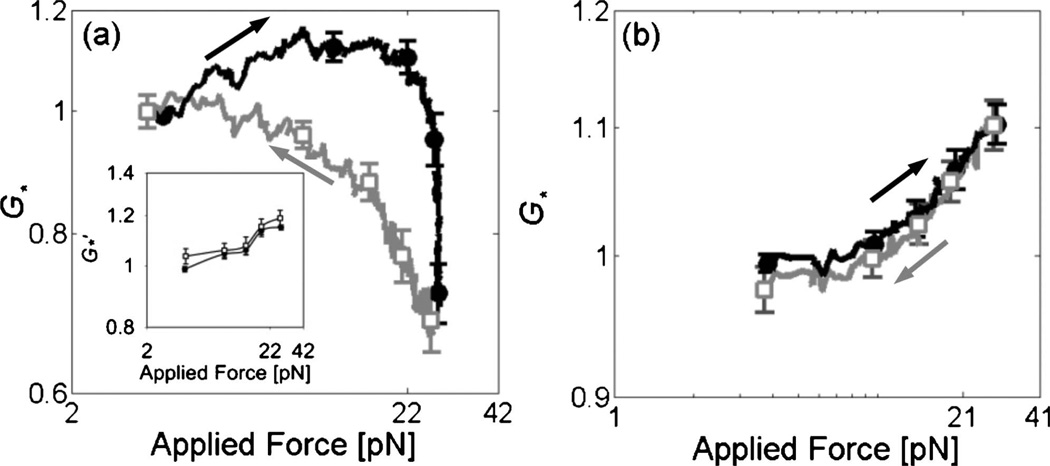
If unbinding occurs under high strains, some degree of irreversibility would be expected, which is in contrast to the potentially reversible process of unfolding or filament buckling [11]. Therefore, we examined the reversibility of mechanical behavior by calculating G for increasing and decreasing strain. For the filamin/F-actin networks (cA =30 µM, Rf =0.01), the mechanical properties were not reversible as indicated by the difference in G′ measured for increasing and decreasing force amplitude while they were reversible in the measurements at smaller deformations [Fig. 4(a)]. This suggests that strain softening in the cross-linked F-actin networks originates from an irreversible process such as unbinding. However, the G′ at the smallest force are similar. It indicates that the network recovers to its original state during the measurements at small deformation, since the bead oscillations are no longer of sufficient magnitude to disrupt bonds that form linking neighboring filaments. The association and dissociation rate constants of ABPs to F-actin are known to be 1–1.3×106 M−1· s−1 and 0.6–0.06 s−1respectively [12, 21, 22]. Considering the in- trinsic kinetic parameters, the duration of the entire experiment, ~3 min, can provide enough time for both remodeling of the network and return to its original form. The irreversibility and hysteresis in Fig. 4(a) should depend on the time scale of the measurements. However, experiments with longer time delay did not exhibit consistent behavior as stress relaxation and reorganization of network structure occurred at long time scales.
FIG. 4.
Normalized elastic modulus as a function of applied force in the measurements for increasing (●, black) and decreasing (□, gray) forces. (a) For filamin/F-actin networks (n=13), network elasticity measured for decreasing stress is not consistent with that for increasing stress. Inset: the stress-dependent mechanical properties are reversible in the measurement at smaller deformations. (b) For streptavidin/biotin-F-actin networks (n=17), similar values of shear modulus are exhibited for increasing and decreasing force.
The role of ABP unbinding in regulating the mechanical properties is further substantiated by comparing these results to experiments in streptavidin/biotin-F-actin networks. Biotinylated actin ([biotin-actin]/[unlabeled actin]=1/4) was polymerized with streptavidin to form a rigidly cross-linked F-actin network (cA=20 µM, Rs=0.01). We estimate the shear modulus as a function of force amplitude using the same method as above. The stress-dependent mechanical properties of the networks cross-linked with streptavidin are shown to be reversible [Fig. 4(b)], in contrast to the irreversible G for the networks cross-linked with filamin. The reversibility observed in streptavidin networks indicates that the strain softening observed in filamin networks is attributable to rupture at cross-links.
Our results present how the mechanical properties of an F-actin network are influenced by cross-link rupture. Although force-induced unbinding is shown to be the dominant mechanism in irreversible strain softening, we cannot exclude other possible contributions, due, for example, to ABP unfolding and F-actin buckling or breakage. In <20% of all experiments, the G measured for increasing and decreasing displacement exhibit similar values {see Fig. S3(a) in the supplementary material [13]}, suggesting that in these cases, the network might maintain its structure by ABP unfolding or F-actin buckling in response to a large deformation. The low probability of reversible behavior is consistent with the observation that unfolding is less frequent than unbinding when a single filamin cross-linking two actin filaments is loaded [12]. Together, occurrence of forced-induced unfolding of filamin seems to be more sensitive to dynamic conditions such as force and loading rate [20]. Even in the network responses, we note that some force-displacement curves exhibit undulation and a plateau region {see Fig. S3(b) in the supplementary material [13]}, which are similar to the saw-tooth pattern [11, 17, 23] and abrupt change [18, 24] of the force slope observed in protein unfolding. The average displacement in the region where the potential unfolding occurs is ≈137 nm, which is less than the total stretching of a single filamin [11]. In an F-actin network under stress, cross-linking proteins are subjected not only to extensional force, but to shear and torsional forces, as well. Complexity in the force application can cause cross-linker unbinding before full extension by unfolding [10].
We have obtained the microscale amplitude-dependent mechanical properties of F-actin gels using the oscillatory response of a microbead, and with linear pulling experiments. By relating the decrease of the network elasticity at high strain with multiple decreases of force in the linear pulling response, we suggest that molecular interactions between actin and ABPs regulate the mechanical properties of F-actin networks. In tests of network reversibility, we have provided evidence to support the theory that strain softening originates from the irreversible process of bond rupture. This study therefore highlights the role of molecular interactions in determining the nonlinear elastic properties of F-actin networks, and by implication, the actin cytoskeleton as well. Further studies using the same cross-linkers with different binding affinity and experiments at longer time scales will also provide a better understanding of microscopic origin of cytoskeleton dynamics.
Supplementary Material
Acknowledgments
We thank F. Nakamura and T. P. Stossel for providing filamin and gelsolin. The work was supported by the NIGMS (GM076689), the NSF (0643745), the Nicholas Hobson Wheeles, Jr. Fund, the W.M. Keck Foundation, the Westaway Research Fund, and the Singapore-MIT Alliance for Research and Technology.
References
- 1.Gardel ML, et al. Phys. Rev. Lett. 2004;93:188102. doi: 10.1103/PhysRevLett.93.188102. [DOI] [PubMed] [Google Scholar]
- 2.Gardel ML, et al. Proc. Natl. Acad. Sci. U.S.A. 2006;103:1762. doi: 10.1073/pnas.0504777103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gardel ML, et al. Science. 2004;304:1301. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 4.Storm C, et al. Nature (London) 2005;435:191. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- 5.Xu JY, Tseng Y, Wirtz D. J. Biol. Chem. 2000;275:35886. doi: 10.1074/jbc.M002377200. [DOI] [PubMed] [Google Scholar]
- 6.MacKintosh FC, Kas J, Janmey PA. Phys. Rev. Lett. 1995;75:4425. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
- 7.Tharmann R, Claessens MMAE, Bausch AR. Phys. Rev. Lett. 2007;98:088103. doi: 10.1103/PhysRevLett.98.088103. [DOI] [PubMed] [Google Scholar]
- 8.Wagner B, et al. Proc. Natl. Acad. Sci. U.S.A. 2006;103:13974. doi: 10.1073/pnas.0510190103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sato M, Schwarz WH, Pollard TD. Nature (London) 1987;325:828. doi: 10.1038/325828a0. [DOI] [PubMed] [Google Scholar]
- 10.Yamazaki M, Furuike S, Ito T. J. Muscle Res. Cell Motil. 2002;23:525. doi: 10.1023/a:1023418725001. [DOI] [PubMed] [Google Scholar]
- 11.Furuike S, Ito T, Yamazaki M. FEBS Lett. 2001;498:72. doi: 10.1016/s0014-5793(01)02497-8. [DOI] [PubMed] [Google Scholar]
- 12.Ferrer JM, et al. Proc. Natl. Acad. Sci. U.S.A. 2008;105:9221. doi: 10.1073/pnas.0706124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.See supplementary material at http://link.aps.org/supplemental/10.1103/PhysRevE.82.011919 for experimental protocol and data.
- 14.Gorlin JB, et al. J. Cell Biol. 1990;111:1089. doi: 10.1083/jcb.111.3.1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.McGough A, Way M, DeRosier D. J. Cell Biol. 1994;126:433. doi: 10.1083/jcb.126.2.433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gardel ML, et al. Phys. Rev. Lett. 2006;96:088102. doi: 10.1103/PhysRevLett.96.088102. [DOI] [PubMed] [Google Scholar]
- 17.Bhasin N, et al. J. Biol. Chem. 2004;279:45865. doi: 10.1074/jbc.M404103200. [DOI] [PubMed] [Google Scholar]
- 18.Kellermayer MSZ, et al. Science. 1997;276:1112. doi: 10.1126/science.276.5315.1112. [DOI] [PubMed] [Google Scholar]
- 19.Merkel R, et al. Nature (London) 1999;397:50. doi: 10.1038/16219. [DOI] [PubMed] [Google Scholar]
- 20.Lee H, et al. Cell. Mol. Bioeng. 2009;2:28. [Google Scholar]
- 21.Goldmann WH, Isenberg G. FEBS Lett. 1993;336:408. doi: 10.1016/0014-5793(93)80847-n. [DOI] [PubMed] [Google Scholar]
- 22.Miyata H, Yasuda R, Kinosita K. Biochim. Biophys. Acta. 1996;1290:83. doi: 10.1016/0304-4165(96)00003-7. [DOI] [PubMed] [Google Scholar]
- 23.Kellermayer MSZ, Bustamante C, Granzier HL. Biochim. Biophys. Acta. 2003;1604:105. doi: 10.1016/s0005-2728(03)00029-x. [DOI] [PubMed] [Google Scholar]
- 24.Tskhovrebova L, et al. Nature (London) 1997;387:308. doi: 10.1038/387308a0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.