Quantitative Imaging of Microtubule Alteration as an Early Marker of Axonal Degeneration after Ischemia in Neurons

Abstract

Neuronal death can be preceded by progressive dysfunction of axons. Several pathological conditions such as ischemia can disrupt the neuronal cytoskeleton. Microtubules are basic structural components of the neuronal cytoskeleton that regulate axonal transport and neuronal function. Up-to-date, high-resolution observation of microtubules in living neuronal cells is usually accomplished using fluorescent-based microscopy techniques. However, this needs exogenous fluorescence markers to produce the required contrast. This is an invasive procedure that may interfere with the microtubule dynamics. In this work, we show, for the first time to our knowledge, that by using the endogenous (label-free) contrast provided by second harmonic generation (SHG) microscopy, it is possible to identify early molecular changes occurring in the microtubules of living neurons under ischemic conditions. This is done by measuring the intensity modulation of the SHG signal as a function of the angular rotation of the incident linearly polarized excitation light (technique referred to as PSHG). Our experiments were performed in microtubules from healthy control cultured cortical neurons and were compared to those upon application of several periods of oxygen and glucose deprivation (up to 120 min) causing ischemia. After 120-min oxygen and glucose deprivation, a change in the SHG response to the polarization was measured. Then, by using a three-dimensional PSHG biophysical model, we correlated this finding with the structural changes occurring in the microtubules under oxygen and glucose deprivation. To our knowledge, this is the first study performed in living neuronal cells that is based on direct imaging of axons and that provides the means of identifying the early symptoms of ischemia. Live observation of this process might bring new insights into understanding the dynamics and the mechanisms underlying neuronal degeneration or mechanisms of protection or regeneration.

Introduction

Ischemia occurs when cerebral blood flow is insufficient to meet the metabolic demand. Poor supply of oxygen (hypoxia) and glucose causes neuronal damage. Ischemia disrupts the neuronal cytoskeleton by causing changes in the phosphorylation of the microtubule-associated protein, Tau (1–5). Microtubules are main components of the neuronal cytoskeletal system. They are essential to maintain the structure of axons and dendrites and are involved in cell trafficking and axonal transport, which are crucial for neurotransmission and normal neuronal function. Under normal conditions, Tau binds to microtubules, stabilizing neuronal structure and integrity (6,7). Ischemia was shown to dephosphorylate as well to increase phosphorylation of Tau (4). A hyperphosphorylation of Tau impedes its interaction with microtubules, which are destabilized (8). Excessive phosphorylation of Tau is also assumed to be the cause of the formation of paired helical filaments-neurofibrillary tangles, seen in Alzheimer disease (7–9). In addition to changes in Tau phosphorylation, Tau can undergo proteolysis (10). Microtubule-associated protein 2 and spectrin, cytoskeleton proteins, are also degraded by activation of calpain (11). Although dephosphorylation of Tau may facilitate the binding of microtubules, there is an increase of Tau susceptibility to the protease calpain (11), and the latter may also compromise the stability of microtubules. It is likely that all these processes will also disturb the stability of the microtubules.

Monitoring structural alterations of microtubules in living neurons after exposure to ischemic conditions will contribute to better understanding of the processes leading to neuronal cell dysfunction and death. In cortical cultured neurons, a model based on oxygen and glucose deprivation (OGD) can be used to produce a controlled neuronal lesion involving progressive axon degeneration. Neuronal OGD models are now well established for in vitro investigations and are widely used in both cellular biology and preclinical stroke research (12). Identification and quantification of structural alterations induced by OGD in living primary neuron cell cultures, in the absence of external contrast, will help us to understand the dynamics of axonal degeneration and neuronal death.

A well-established high-resolution imaging technique that can be used for such a task is based on exploiting the second harmonic generation (SHG) signal originated from the axons' microtubules (13–15). The SHG signal is produced when two excitation photons, upon interacting with matter (i.e., the sample), create one of double energy (i.e., double-frequency or at half the excitation wavelength). For this frequency doubling conversion process to occur, media-lacking inversion of symmetry is required. At the molecular level, such a condition is present in polar molecules (i.e., those possessing a permanent electric dipole) (16). Examples of such SHG active molecules are amylopectin (17), collagen triple helix (18–21), myosin (18–22), and tubulin heterodimers (23,24). Furthermore, an aligned array of such polarized molecules is able to produce, through constructive interference, an efficient SHG signal (14). This is indeed the case for starch, collagen, muscle, and microtubules, respectively. In this last particular case, SHG signal arises only from polarized microtubules such as those in the axons of neurons (13,14,25) and in other nonneuronal cell structures such as axonemes (23) and mitotic spindles (26).

This requirement on such particular molecular organization has two important implications in SHG microscopy:

Firstly, by analyzing the SHG response upon rotation of the linearly polarized excitation beam (referred to as PSHG microscopy (27,28)) it is possible to obtain structural information from the molecule itself.

Secondly, this is an intrinsic material property, not requiring any sample treatment, labeling, or staining, or genetic modification for generating contrast. This is highly advisable for in vivo microscopy studies. These properties are in contrast to other studies in ischemia where fluorescent signal was used (5).

In this study we identify, for the first time to our knowledge, early structural changes occurring in the microtubules of axons of neurons in vitro under the effect of different degrees of OGD, simulating mild or severe ischemic conditions. For that purpose, we use a three-dimensional generalization of the PSHG technique (without the use of an analyzer in the detection path) and analyze the PSHG images on a pixel-by-pixel basis. We find that in neurons exposed to a brief (60-min) period of OGD, no observable effects can be measured with PSHG when compared to the normoxic or control cultures. However, PSHG shows significant changes after exposing the neurons to 120-min OGD, which can be attributed to structural changes in microtubules. Such identification and quantification of structural neuronal changes could be used for monitoring and reflecting early signs of neuron degeneration, not only under ischemia but also in any other condition in which microtubules could be affected.

Materials and Methods

Neural cultures

Both primary cortical neuron and mixed neuron-glia cultures were prepared from 18-day-old Sprague-Dawley rat embryos (Charles River Laboratories, Wilmington, MA) as described earlier (24). Briefly, animals were anesthetized and sacrificed by cervical dislocation. All procedures were approved by the Ethical Committee for Animal Use at the University of Barcelona. Cells were resuspended in Modified Eagle’s Medium supplemented with 10% fetal calf serum and 100 μg/mL gentamycin and plated onto poly-L-lysine (5 μg/mL)-precoated glass-bottom dishes at a density of 1273 cells/mm² for mixed cultures. Neuron-enriched cultures were prepared similarly (final density 764 cells/mm²) but medium was partly changed on the seventh day in vitro with Modified Eagle’s Medium supplemented with B27, and cytosine arabinoside was added on the fourth day in vitro to limit glial proliferation. PSHG imaging experiments in neuronal processes were performed on the seventh day in vitro in both culture types.

Treatments

For performing oxygen and glucose deprivation (OGD), the culture medium of mixed neuron-glia cells was replaced by a glucose-free HEPES buffer (NaCl 135 mM, KCl 5 mM, CaCl₂ 2H₂O 1.8 mM, MgSO₄ 7H₂O 0.62 mM, and HEPES 10 mM). Cells were then incubated for 60 or 120 min in an hypoxic incubator (GalaxyR/RS Biotech; New Brunswick Scientific, Enfield, CT) containing 94% N₂, 5% CO₂, and 0,6% O₂. Reoxygenation was obtained by replacing HEPES buffer with normal feeding media and cells were returned to a regular incubator (95% atmospheric air and 5% CO₂). Normoxic conditions were achieved incubating the cells for 60 or 120 min with the same HEPES buffer supplemented with 5.5 mM glucose in a regular incubator (95% atmospheric air and 5% CO₂). Control sister cultures, kept in a regular incubator with no medium changes, were processed in parallel. Neuron-enriched cultures were treated with 0.5 μM colchicine. Six different mixed cultures and two different neuron-enriched cultures were used. PSHG imaging experiments were performed from 2 to 4 h after reoxygenation.

For glial fibrillary acidic protein (GFAP) and Tau immunocytochemistry, control cultures were fixed in 4% paraformaldehyde for 30 min, permeabilized 5 min with Triton 0.5% in phosphate-buffered saline (PBS), blocked 30 min in PBS+3% goat serum at room temperature, and incubated overnight at 4°C with rabbit anti-GFAP 1:500 (Dako North America, Carpinteria, CA) and mouse anti-Tau 1:300 (Millipore, Billerica, MA). The following day, cultures were incubated 1 h at room temperature with anti-rabbit Alexa Fluor 546 or anti-mouse Alexa Fluor 488 secondary antibodies. Photomicrographs were acquired in a model No. IX 71 fluorescence microscope (Olympus, Melville, NY).

PSHG microscope

The setup is based on an adapted inverted microscope (TE2000-U; Nikon, Tokyo, Japan) with the laser scanning performed by a pair of galvanometric mirrors (Cambridge Technology, Nyon, Switzerland). The whole microscope unit is enclosed in a plastic box, which was heated to control the temperature at 36.7°C. A 60× (NA = 1.4, Plan Apo-Achromat; Nikon) objective was used for excitation, while for collection of the signals in the forward direction a 1.4 NA (Nikon, Japan) condenser was used. For the excitation source, we used a Kerr lens mode-locked Ti:Sapphire laser (MIRA 900fl; Coherent, Santa Clara, CA), with pulses of 160 fs at a repetition rate of 76 MHz, and operated at a central wavelength of 810 nm. After the galvanometric mirrors, we placed a linear polarizer that was followed by a zero-order λ/2 wave plate (QWPO-810; CVI Melles Griot, Leicester, UK) on a motorized rotational stage (M-060.DG; Physik Instrumente, Cranfield, Bedford, UK). This was rotated in steps to change the polarization at the sample plane. A telescope arrangement was used to ensure that a collimated beam was filling the back-aperture of the objective lens.

In the forward collection geometry, a proper mount and detection unit was implemented. This home-made mount contained a long-wave-pass dichroic beamsplitter (FF665; Semrock, Rochester, NY), a BG39 filter (Schott, Mainz, Germany), a 10-nm FWHM band pass filter centered at 405 nm (FF01-405/10-25; Semrock), and a bi-alkali photomultiplier tube (PMT, H9305-03; Hamamatsu, Hamamatsu City, Japan). In the backward collection geometry of the microscope, we choose to use only a BG39 filter (Schott) and record any signal reaching a bi-alkali PMT (H9305-05; Hamamatsu). Any effect on the depolarization of the fundamental beam introduced by the several optical components before the sample plane was assessed by measuring the mean power of the fundamental for the polarization steps of the retardation-plate, as a function of the rotation angle of an analyzer positioned parallel and perpendicular to each incoming linear polarization. The fundamental input average power, under rotation of the linear polarization (nine steps of 20°), exhibited a mean extinction coefficient ratio of 63:1 and 25:1, without and with the 60× objective, respectively.

Second harmonic generation in microtubules

As mentioned before, axons are composed of an organized array of polarized microtubules that are able to produce an efficient SHG signal. Such microtubules are composed of tubulin, which in its more basic unit consists of the alpha-beta (α-β) tubulin dimers. These heterodimers possess a permanent electric dipole (13,14). Upon interaction with high intense light, a nonlinear dipole moment μ is induced. The component μ_ν along the molecule axis ν for a single molecule can then be described by

$${\mu }_{\nu }=\sum _{\kappa \zeta }{\beta }_{\nu \kappa \zeta }{E}_{\kappa }{E}_{\zeta },$$ (1)

where E_i is the light excitation electric field component in the ν, κ, and ζ molecule coordinate system and β_νκζ is the νκζ component of the microscopic third-rank hyperpolarizability tensor β. The tensor β is the one ultimately responsible for the SHG signal at the molecular level. The description of the SHG conversion is usually simplified by considering a main component β_ννν in one direction (16). In microtubules, β_ννν is associated to the α-β tubulin dimer (24). Then, the macroscopic SHG response in microtubules, which is described by a second-order susceptibility tensor χ⁽²⁾, results from the coherent addition of β_ννν. In our approach, the susceptibility tensor element χ_ijk in a region with a density N of α-β tubulin dimers can then be written as

$${\chi }_{ijk}=N\langle (\hat{i}·\hat{\nu })(\hat{j}·\hat{\nu })(\hat{k}·\hat{\nu })\rangle {\beta }_{\nu \nu \nu },$$ (2)

where 〈⋅⋅⋅〉 denotes average; i,j,k are indices indicating the microtubule coordinate system x,y,z; and $\hat{i}$ indicates a unit vector. Microtubules possesses cylindrical symmetry, resulting in only two tensor independent elements: χ_xxz = χ_yyz = χ_zyy =χ_zxx and χ_zzz (29), where z denotes the microtubule main symmetry axis along which it is oriented. Using an azimuth φ and a zenith θ angle to describe the ν direction and assuming a constant distribution of β_ννν in the azimuth plane (due to the microtubule cylindrical symmetry), the dependence of χ_ijk with φ disappears and the ratio between the two χ⁽²⁾ tensor independent elements can be expressed as (18)

$$\frac{{\chi }_{zzz}}{{\chi }_{zxx}}=\frac{2}{{\tan }^2{\theta }_e},$$ (3)

where θ_e can be interpreted as the angle of the β_ννν associated to the α-β tubulin dimer with respect to the symmetry axis z of the microtubules (see Fig. 1 c).

Figure 1.

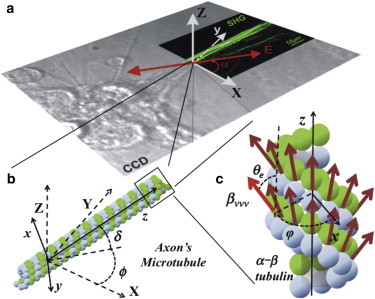
Coordinates system of the three-dimensional PSHG biophysical model for microtubules. (a) Superposition of bright field and SHG images from a neuron with the laboratory coordinate system X, Y, Z. SHG image corresponds to microtubules. (Double headed arrow) Orientation of the polarized excitation light. (b) Schematics of a microtubule composed of α- and β-tubulin dimers. The microtubule symmetric axis z orientation is determined by the off-plane angle δ and the in-plane angle ϕ. (c) Magnification of the microtubule showing the α-β tubulin heterodimer distribution. (Brown arrows) Hyperpolarizability β_ννν directions. (Hightailed red arrow) Angle θ_e and φ for β_ννν. The dimensions of the figure and directions are illustrative and do not correspond to reality.

The PSHG technique

The induced nonlinear dipole, when excited with different incoming linear polarizations (or equivalently by rotating the sample), provides a SHG response that is characteristic of the local molecular geometrical arrangement. Specifically, we assume that the laboratory coordinate system is X-Y-Z. The laser is propagating along the laboratory Z axis and its linear polarization can be rotated in the X-Y plane in an angle α with respect to the Y axis (see Fig. 1 a). The coordinate system of the microtubules is chosen in such a way that the Y axis is contained in the X-Y plane and the Z axis coincides with the principal symmetry axis (major axis orientation) of the microtubule (Fig. 1 b). With this geometry, the relation between the lab and the microtubule frames of reference is given by the elevation angle δ and the in-plane orientation angle ϕ. Then, the detected intensity in terms of the polarization α and microtubule ϕ orientations with respect to the lab coordinate system is given by

$$I^{2\omega }\left(\alpha \right)=I_0\left\{{\text{sin}}^2\left[2\left(\alpha -\varphi \right)\right]+{\left({\text{sin}}^2\left[\alpha -\varphi \right]+A{\text{cos}}^2\left[\alpha -\varphi \right]\right)}^2\right\},$$ (4)

where A is the anisotropy parameter. Note that A in Eq. 4 determines the SHG response with the polarization. To understand the nature of this differentiated SHG response, we follow the theory developed in Psilodimitrakopoulos et al. (30). Then, A can be written as

$$A=\frac{{\chi }_{zzz}}{{\chi }_{zxx}}{\text{cos}}^2\delta +3{\text{sin}}^2\delta ,$$ (5)

showing that there are two contributions that can cause changes in A: the elevation angle δ and the tensor ratio χ_zzz/χ_xxz.

Note that χ_zzz/χ_xxz is related to the effective orientation θ_e with respect to the microtubule axis z (Eq. 3), which in turn is determined by the polarization properties of the α-β tubulin dimer. A usual approach to determine the relation between the anisotropy parameter A and the angle θ_e is to set δ = 0 (the microtubules long axis z is assumed to lay parallel to the sample plane). Then Eq. 5 reduces to A = χ_zzz/χ_xxz, and using by Eq. 3 the effective angular orientation θ_e of the molecule nonlinear dipole can be found. Under this approach, any variation in A is attributed to a variation in χ_zzz/χ_zxx, and therefore to a change on the orientation of the β_ννν associated to the molecule, i.e., to a molecular change of the α-β tubulin dimer. Otherwise, an alternative approach can be assumed by fixing the value for χ_zzz/χ_zxx (30). This approach is equivalent to assuming that the α-β tubulin dimer does not change and any change in the experimentally retrieved anisotropy parameter A is attributed to the angle δ that describes off-plane microtubules. Then, using Eq. 5, the angle δ can be found. In a real situation, a change in the anisotropy parameter A is the result of both approaches described above, and the data must be carefully analyzed to determine the main contribution.

To retrieve the anisotropy parameter A, we use the fast-Fourier-transform (FFT)-based retrieving approach reported in Amat-Roldan et al. (31), Réfrégier et al. (32), and Gusachenko et al. (33). For that, Eq. 4 can be rewritten as a sum of Fourier components as (31–33)

$$I^{SHG}\left(\alpha \right)=a_0+a_2\text{cos}\left[2\left(\alpha -\varphi \right)\right]+a_4\text{cos}\left[4\left(\alpha -\varphi \right)\right],$$ (6)

where the absolute value of coefficients a₀, a₂, and a₄ and ϕ are the unknown variables that are retrieved using the FFT-based approach. This is performed in every pixel and therefore, the result is insensible to the main orientation of the microtubule in the image. Once a₀, a₂, and a₄ are determined, the anisotropy parameter A in microtubules can be obtained as

$$A=\sqrt{\frac{\left|a_0\right|+\left|a_2\right|-\left|a_4\right|}{\left|a_0\right|-\left|a_2\right|-\left|a_4\right|}}+\epsilon .$$ (7)

Note that the determination of the a₀, a₂, and a₄ coefficients are subjected to errors such as electronic noise and others such as the effect of axial components in the focus (34), depolarization (34), and sample birefringence (35). All these errors are modeled in the error coefficient ε in Eq. 7. Nine polarizations are considered adequate to retrieve the four free parameters of Eq. 6 (22).

The above model does not differentiate between Gaussian and cone molecular distributions, it only accounts for their relevant changes. A more general model, without a priori knowledge of the symmetry and molecular distribution, has been very recently presented (36,37). Nevertheless, this is a two-dimensional model that requires the molecule axis of symmetry to lie parallel to the sample plane. Our approach consists of using a three-dimensional model, which attributes changes of the anisotropy parameter A to the tilted off-plane filaments present in thick samples.

Statistics

To compare two groups we used the t-test. To compare all groups, the nonparametric Kruskal-Wallis test was performed with a post-hoc Dunn test in GraphPad Prism 4.00 for Windows (GraphPad, San Diego, CA). Differences were considered significant at P < 0.05. Results are shown as mean ± SE (standard error of the mean).

Results

Earlier studies show that the SHG signal in neurons arises from the microtubules contained in their axons (13–15,24,25). Therefore, we sought to determine whether it was possible to detect a PSHG signal from axons in living cortical cultured neurons. Throughout our experiments, we fixed the gain in the PMT and we fixed the excitation power to 10 mW at the sample plane. In this regime, no observable damage occurred for long imaging periods of time (>2 h). We observed that the SHG signal was mostly generated in the forward direction. Although weak from a single axon, bundles of several axons offered a strong SHG signal. This was expected, because the SHG intensity is quadratically dependent upon the concentration of SHG scatterers (the microtubules), and the higher the number of axons excited within the excitation volume, the higher the generated SHG signal. This signal was lost when we treated the neurons with colchicine (a microtubule-depolymerization agent (25)), strongly indicating that the SHG was indeed microtubule-generated. Specifically, we observed ∼92% reduction in the SHG after adding colchicine in the culture (data not shown). In our hands, when neurons are cultured in the presence of glial cells, axon bundles were thicker. Therefore, we decided to perform our experiments (normoxia-OGD) in mixed cultures. The SHG was specifically recorded in axons. These cannot be mistaken for glial processes because axons are much longer and thicker than astroglial processes, as shown by GFAP-Tau immunocytochemistry in Fig. 2.

Figure 2.

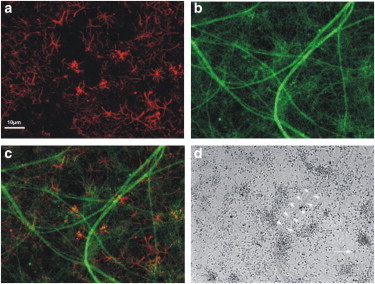
Photomicrographs of neuron and astrocyte processes in mixed cultures. Immunocytochemistry for glia fibrillary acidic protein (GFAP) (a) and Tau protein (b). Merge of A and B (c). Phase contrast image of the culture. (d) (Open arrowheads) Axons; (open arrow) an astrocyte. Scale bar, 100 μm.

We then proceeded to perform the PSHG analysis and retrieve the value of the anisotropy parameter, A, from cortical cultured neurons, including control (n = 9), normoxia (n = 19), and OGD applied during 60 min (n = 4) and OGD during 120 min (n = 38). Here n is the number of PSHG experiments, which are performed in four different regions in each dish. In Fig. 3 we show a typical intensity PSHG image from a control sample, acquired for each of the nine (0–160°) linear excitation polarization steps with increments of 20°. The time needed to acquire all the PSHG data was >3 min (we took three images of the same polarization, for each of the nine polarization steps). Fig. 3 shows how the SHG signal in every pixel varies with the incoming polarization. This reflects the effect of the anisotropy parameter A in the intensity modulation given by Eq. 3. In microtubules, the maximum signal is observed when the incoming linear polarization was parallel to the axons and minimum SHG signal when perpendicular. To retrieve the anisotropy parameter, the PSHG signal modulation from each pixel (the change of the SHG signal intensity due to the rotation of the excitation linear polarization observed in Fig. 3) was normalized to each pixel’s maximum intensity.

Figure 3.

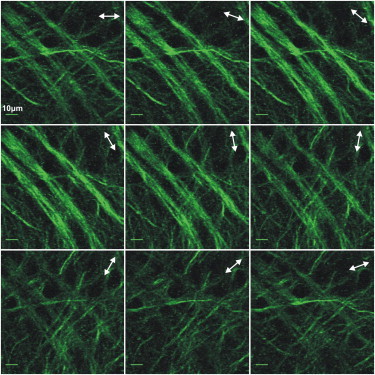
PSHG images of control cortical cultured neurons. (Arrows) Excitation linear polarization (nine steps rotation of 20°). Scale bar shows 10 μm. Each image of each polarization is composed by the average intensity of three images.

Moreover, only pixels that showed a polarization-dependent SHG signal modulation values >50% of the minimum signal were kept. The rest were considered noise and were removed. As an example, the resulting nine images of Fig. 3 were analyzed with the FFT PSHG algorithm. The result is shown in Fig. 4, a–c. The same procedure was applied to a different set of cultured neurons in which OGD was applied for 120 min. The results are displayed in Fig. 4, d–f. By simply comparing the intensity SHG images in Fig. 4, a and d, it is not possible to see any difference between the two samples. The situation is similar when the pseudocolor images of the retrieved anisotropy parameter A are compared (Fig. 4, b and e).

Figure 4.

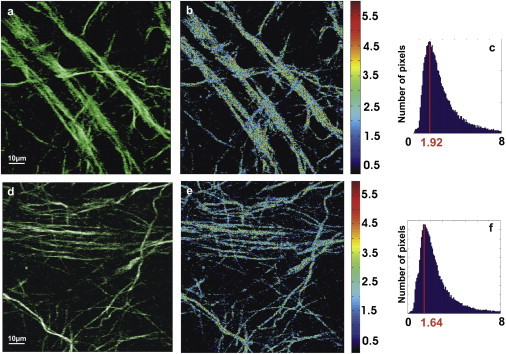
PSHG resulting images. (a) Noise filtered intensity image showing those pixels that are kept for analysis in control sample. (b) Image formed from the pixel-by-pixel values of the anisotropy parameter A. (c) Pixels’ histogram for the value of A for control with peak at A_peak = 1.92 and width = 1.88. (d) Noise-filtered intensity images of OGD-120 min. (e) Image formed from the pixel-by-pixel values of the anisotropy parameter A. (f) Pixels’ histogram for the value of A for OGD with peak at A_peak = 1.64 and width = 1.98.

In both cases a homogeneous spatial distribution of A is observed and it is difficult to identify differences. To quantify differences between images, we can make use of image-processing techniques. A simple and useful approach is to use the image histograms, which represents the number of pixels for each tonal value in an image. In our case, the tonal value corresponds to the retrieved value of the A parameter (22). Fig. 4, c and f, corresponds to the image histogram from Fig. 4, parts b and e, respectively. In this case, the histograms are significantly different. In the case of control, the anisotropy parameter, A, has its maximum frequency at A = 1.92, having a width (defined as 2σ) of 1.88. In the case of OGD-120 min, the peak is shifted to A = 1.64, and there is a measurable increase in the histogram’s width to 1.98. This result shows that variations in the histogram of the anisotropy parameter can be used to quantify the structural differences between control and ischemic neurons by comparing their peaks and width. To compare all groups, we first pooled the normo60min and normo120min conditions because using the t-test, we found that they were not significantly different. The results obtained from control and normoxic cultures were also undistinguishable.

We thus proceed to retrieve the value of A for different neuron culture samples and analyze the histogram of each image, obtaining its peak and width. The statistical results for the two parameters are shown in Fig. 5. When comparing the results for control and normoxia samples, we found that there were no significant differences in the peak (Fig. 5 a) nor in the width (Fig. 5 b) of the anisotropy parameter A (P > 0.05 in both cases). This means that normoxia does not affect the structure of the microtubules, or else that our technique is not sensitive to any change that could have happened. The same occurs for the samples with 60 min of OGD when compared with the normoxia: there is a reduction in the peak position of A, and width is slightly reduced, but these changes are not significant (P > 0.05). The situation drastically changed for samples subjected to 120 min of OGD. Comparing the control and the 120-min OGD conditions, we found that the peak in the A shifts on average to lower values in ischemic conditions. As it can be seen in Fig. 5, in this case, the mean peak value of the anisotropy parameter A is A = 1.720. This is significantly lower than the mean peak value found for the exposure to normoxic conditions: 2.107 (P < 0.001). In addition to the clear differences in the peak values of A between normoxia and samples after 120 min of OGD, the widths of the histograms were larger in the 120-min OGD condition than in the control condition (Fig. 5 b). The difference was significant, resulting in P < 0.05.

Figure 5.

Measurement of the anisotropy parameter A, for control, normoxia, OGD at 60 min, and OGD at 120 min. (a) The peak value of the anisotropy parameter A, A_c = 1.981 with mean ± SE = 0.079 for control, A_n = 2.107, mean ± SE = 0.051 for normoxia, A_OGD60 = 1.982 mean ± SE = 0.069 for OGD60min, and OGD120min with A_OGD120 = 1.720, mean ± SE = 0.052. (b) Statistics for the width of the pixels histograms of A, w_c = 1.876, mean ± SE = 0.022 for control w_n = 1.82, mean ± SE = 0.007 for normoxia w_OGD60=1.83, mean ± SE = 0.014 for OGD-60, and w_OGD120 = 1.996, mean ± SE = 0.012 for OGD120.

Discussion

All the above results show that by either using the peak value and/or the width of the pixels’ histograms of the anisotropy parameter A, one could mark significant differences between the ischemic and normal neurons. Note that although measurements of the histograms of the different samples can be greatly affected by errors, those are systematic, and throughout these set of experiments, care was taken to ensure that they were the same for the analyzed samples. This indicates that any change in the histograms can be related to a change in the contrast mechanism in the sample, which in our case can be related to structural changes in the microtubules by considering Eq. 5. In particular, as outlined in The PSHG Technique, Eq. 5 offers two explanations on the cause that can change the histograms (30):

• Case 1. The value of A can change due to a variation in the value of the tensor ratio χ_zzz/χ_zxx; and

• Case 2. The histogram can change due to an increase in δ, i.e., an increase of microtubules oriented off-plane.

In the first case, a variation in the value of the tensor ratio χ_zzz/χ_zxx can be related to a change in the angle θ_e between the hyperpolarizability β_ννν orientation (associated to the α-β tubulin) and the microtubule axis z through Eq. 3. In particular, the shift in the peak distribution for the anisotropy parameter from A = 2.107–1.720 can be interpreted as an average change in the orientation from θ_e = 44.3–47.1°. The statistical analysis showed that this change is significant (P < 0.001).

We advance two geometrical possible interpretations of this shift: The first one is a change in the heterodimer orientation with respect to the microtubule symmetry axis z, as sketched in the change from Fig. 6, panel a, to Fig. 6, panel b. The second possibility is a compression or broadening of the heterodimer, as shown in Fig. 6 c. However, while this last possibility cannot be related to any known phenomenon affecting the heterodimer, the change of orientation is consistent with a conformational change of the β-tubulin monomer from guanosine 5-triphosphate (GTP) to guanosine 5-diphosphate (GDP) observed in nonliving samples (38–41). This conformational change favors dissociation and causes a change of 27° in the orientation of the α-β-tubulin heterodimer with respect to the microtubule symmetry axis (40). This is consistent with the average shift in the peak histograms detected after 120 min OGD, which could indicate an increase in the population of conformational changes from GTP to GDP tubulin and the start of the microtubule dissociation. In addition, these conformational changes could also be consistent with changes in the phosphorylation of the Tau microtubule-associated protein, uniquely localized in microtubules in axons—a common feature of ischemic neurons, promoting destabilization of the axon and the neuronal cytoskeleton (1–11). These evidences indicate that the PSHG analysis is able to identify microtubule degradation induced by OGD in its initial stages. It also indicates that the conformational changes observed in nonliving samples (38–41) could also occur in living neuronal cells. Importantly, these changes are not detected for 60 min OGD (mild ischemia) but appear after 120 min OGD, indicating that, after an initial resistance to ischemia, the microtubule alterations described here are early markers of axonal degeneration and neuronal death.

Figure 6.

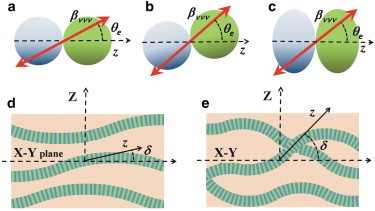
Biophysical interpretation of the change in the anisotropy parameter A, using Eq. 5. (a) Original α-β tubulin heterodimer, with the direction of the hyperpolarizability β_ννν given by the angle θ_e. (b) Geometrical interpretation of a shift in the angle θ_e caused by a change in the heterodimer orientation. This interpretation is consistent with conformational changes from guanosine 5-triphosphate (GTP) to guanosine 5-diphosphate (GDP) of the β-tubulin. (c) Alternative geometrical interpretation consisting of a hypothetical compression of the heterodimer. (d) Ordered microtubules results in a narrower range of angles δ than (e) disordered microtubules. As a result, the width of the A histogram increases for a disordered microtubule.

The second contribution, i.e., the variation in the elevation angle δ, is sketched in Fig. 6, d and e. Initially, because the samples were prepared with the axons lying mainly parallel to the focal plane of the microscope, the microtubules are expected to be oriented around δ ≈ 0. Then, Eq. 5 suggests that the value of A corresponding to the peak histogram should be close to the tensor ratio χ_zzz/χ_zxx. After this point, it is clear from Eq. 5 that an increase in the angle δ would result in a shift on the peak values of the anisotropy parameter close to A = 3. However, the shift in the histogram peak measured for 120 min OGD was in the contrary direction, i.e., to lower values of A. This is only possible if all the microtubules would decrease the value of δ, i.e., increasing the order by induction of fiber lying parallel to the focal plane—a situation that is unlikely to happen because injury tends to increase tissue disorder, at least during the initial stages. The most plausible explanation is that under OGD, the range of angles δ at which the microtubule is oriented increases, resulting in a more disordered arrangement of microtubules (transition from Fig. 6, d and e). As a result, the width of the histogram would increase (30), partially explaining the increase on the width shown in Fig. 5 b after 120 min of OGD.

Conclusions

In this study, we present, for the first time to our knowledge, a quantitative, label-free and all optically based technique to monitor the degeneration of microtubules in axons of living primary neuronal cells during OGD progression. This methodology allows identifying subtle structural changes of the α-β tubulin dimer (the hyperpolarizable molecule) in microtubules in axons from cultured cortical neurons. In particular, the minimally invasive, high-resolution, polarization-sensitive, second harmonic generation (PSHG) imaging was able to quantitatively assign differences between healthy and ischemic neurons.

Our experimental results and analysis showed that after 120 min of OGD, two phenomena occurred at the microtubules’ level: First, a significant change occurs in the orientation of the α-β tubulin dimer, which can be related to conformational changes from GTP to GDP tubulin and the beginning of the microtubule dissociation (38–41). Second, a significant increase in the microtubule disorder is identified. The conformational change is consistent with the well-known modification in the phosphorylation of Tau microtubule-associated protein (1–11) and with studies performed in nonliving samples (38–41). It is important to state that these changes were not observed for 60 min of OGD, showing certain neuron resistance to ischemic processes. This procedure could be used to follow not only ischemic neurons but also other types of neurodegenerative illnesses or the study of neuroprotective agents.