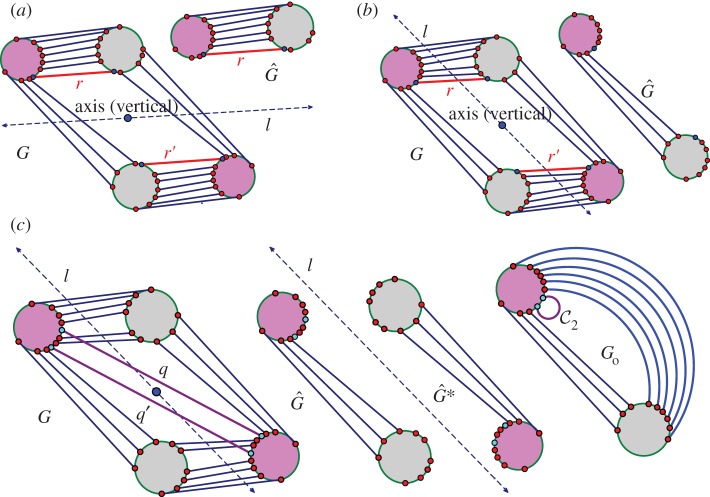
Figure 8.

Three samples for the runs of algorithm 7.2. See also [35] for a detailed demonstration of the symmetric pebble game. (a) The algorithm declares the edges r and r′ to be in R₁ in the first step, if tested last in the run on 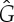. It accepts all other edges not crossing ℓ in 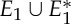and all bridging edges (crossing ℓ) in E₂. So, in step (1), the algorithm predicts no non-trivial motion since |E₁∪E*₁∪E₂|= 6+6+6=18=6|B|−6. In step (2), the algorithm predicts a non-trivial symmetric motion since |E₁∪E₃|=6+3=9<10=6|B₀|−2. (b) The algorithm (applied to the same graph as in (a), but with a different choice of representatives for the vertex orbits) accepts all edges not crossing the new line ℓ in 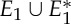. All bridging edges except r and r′ are placed in E₂, while r and r′ (tested last among bridging pairs) are placed in R₁. So the counts are |E₁∪E*₁∪E₂|=3+3+12=18=6|B|−6 (again predicting no non-trivial motion in step (1)) and |E₁∪E₃|=3+6=9<10=6|B₀|−2 (again predicting symmetric flexibility in step (2)). (c) All edges not crossing ℓ are placed in 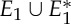, all bridging edges except q and q′ are placed in E₂, and q and q′ are placed in Q. Therefore, in step (1) of the algorithm we obtain |E₁∪E*₁∪E₂|= 3+3+12=18=6|B|−6, and in step (2) we obtain |E₁∪E₃|=3+7=10=6|B₀|−2, and hence no non-trivial motion is detected. (Online version in colour.)