Figure 2. Angular Dependence of Local Thiele Modulus in Elliptically Shaped Cells.
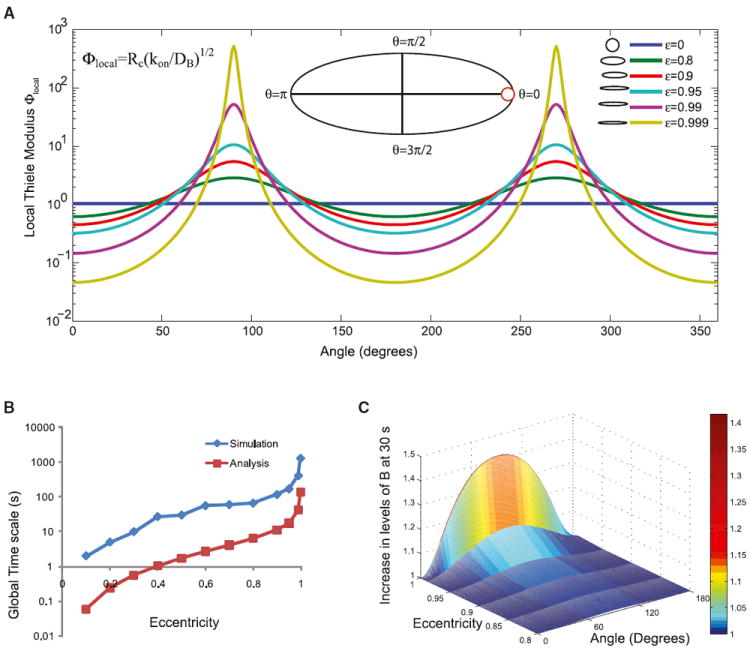
(A) Local Thiele modulus varies along the angle in an ellipse and results in competing reaction and diffusion processes along the membrane. The range of the local Thiele modulus also increases with increasing eccentricity of the ellipse. Inset shows a reference ellipse with the different angles marked. The red circle shows the osculating circle that determines the radius of curvature at the point θ = 0.
(B) The global timescales from analysis and numerical simulations follow similar dependence on eccentricity. Note that the simulation includes the timescale of the reaction, whereas the analysis is based on size and diffusivity alone.
(C) The fold change in component B along the membrane is calculated by normalizing the membrane concentrations by the value of B at θ = 0. The fold change in B depends on the eccentricity of the ellipse, and as the ellipse becomes more elongated (compare ε = 0.9 to ε = 0.999), the fold change in B increases.
