Denoising of 4D Cardiac Micro-CT Data Using Median-Centric Bilateral Filtration

Abstract

Bilateral filtration has proven an effective tool for denoising CT data. The classic filter utilizes Gaussian domain and range weighting functions in 2D. More recently, other distributions have yielded more accurate results in specific applications, and the bilateral filtration framework has been extended to higher dimensions. In this study, brute-force optimization is employed to evaluate the use of several alternative distributions for both domain and range weighting: Andrew's Sine Wave, El Fallah Ford, Gaussian, Flat, Lorentzian, Huber's Minimax, Tukey's Bi-weight, and Cosine. Two variations on the classic bilateral filter which use median filtration to reduce bias in range weights are also investigated: median-centric and hybrid bilateral filtration. Using the 4D MOBY mouse phantom reconstructed with noise (stdev. ~ 65 HU), hybrid bilateral filtration, a combination of the classic and median-centric filters, with Flat domain and range weighting is shown to provide optimal denoising results (PSNRs: 31.69, classic; 31.58 median-centric; 32.25, hybrid). To validate these phantom studies, the optimal filters are also applied to in vivo, 4D cardiac micro-CT data acquired in the mouse. In a constant region of the left ventricle, hybrid bilateral filtration with Flat domain and range weighting is shown to provide optimal smoothing (stdev: original, 72.2 HU; classic, 20.3 HU; median-centric, 24.1 HU; hybrid, 15.9 HU). While the optimal results were obtained using 4D filtration, the 3D hybrid filter is ultimately recommended for denoising 4D cardiac micro-CT data because it is more computationally tractable and less prone to artifacts (MOBY PSNR: 32.05; left ventricle stdev: 20.5 HU).

1. INTRODUCTION

The bilateral filter (BF) [1] is an edge-preserving smoothing filter constructed from the product of two kernels: (1) a spatially-invariant domain kernel which weights by spatial distance and (2) a spatially-varying range kernel which weights by intensity difference. Depending on the functions used to construct each kernel, their product performs a weighted average of similar pixels while effectively ignoring dissimilar pixels, balancing edge preservation against the smoothing of noise. While this sounds ideal, in practice, the BF flattens intensity gradients, yielding piecewise-smooth or “painted” results. Several papers have addressed this problem by explaining the BF within the broader framework of kernel structuring and regression and proposing modifications to the basic filter[2][3]. When filtering photographs, these modifications noticeably improve results; unfortunately, they also tend to increase computation time. Here, we investigate the application of bilateral filtration to cardiac micro-CT data. Unlike noisy photographs, the true information underlying noisy CT data is piecewise-smooth (to a very close approximation) because of the relatively low contrast sensitivity of CT. We expect BF may prove ideal for denoising our cardiac micro-CT data without relatively high computational costs.

The potential of BF in CT applications such as dose reduction has already been demonstrated, particularly when the filter is extended to four dimensions (x, y, z, time)[4]. The purpose of this work is to optimize the performance of BF for the removal of noise from 4D, murine cardiac micro-CT data by extending ideas which have proven effective in 2D. Specifically, this paper builds upon the 2D work of Francis and de Jager[5] which shows the benefits of replacing one or both Gaussian distributions of the classic BF[1] with another smooth or even piecewise distribution. The work of Francis and de Jager[5] also attempts to address an innate short-coming of the classic BF, the fact that the range weights are biased by noise in the voxel on which the kernel is centered. Here, we investigate their proposed solution to this problem, calculating range weights from the median value within the kernel (median-centric BF). We also propose a combination between the classic and median-centric BFs.

2. METHODS

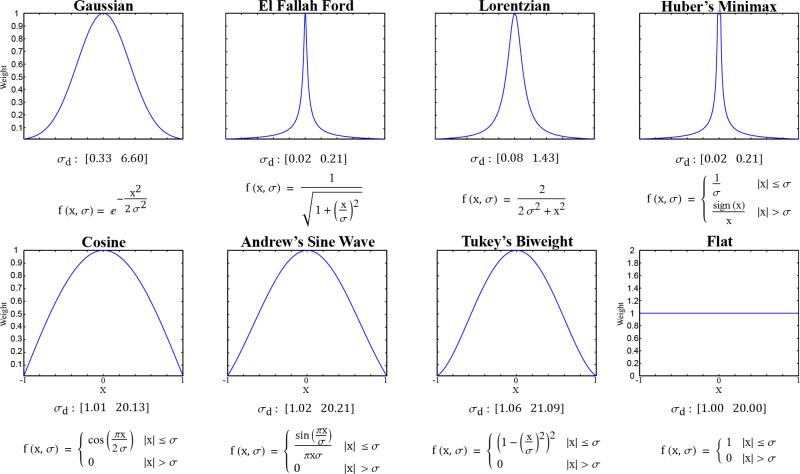
Following the work in Francis and de Jager[5], several robust weighting functions were investigated for both domain and range weighting: Andrew's Sine Wave (AW), El Fallah Ford (EFF), Gaussian (Gauss), Lorentzian (Lor), Huber's Minimax (HMM), and Tukey's Bi-weight (Tukey). Two additional weighting functions were also investigated: Cosine (Cos) and Flat. Similar to the Gaussian function used for both the domain and range in the classic filter, all of these functions are symmetric about and ultimately decrease with distance from zero. The functions can be further divided into continuous functions (e.g. Gauss) which approach zero as the distance from zero goes to infinity and piecewise functions (e.g. Flat). As a domain weighting function, the Flat function was particularly relevant because it gave equal weight to all voxels within a certain radius, converting the BF to an intensity-weighted average. One additional function, Average, was used only for range weighting, converting the BF to a spatially-invariant averaging filter and creating a control against which the performance of the true BFs could be evaluated. A summary of all weighting functions and their general shapes can be found in Figure 1.

Figure 1. Domain and Range Weighting Functions.

All weighting functions are normalized by the largest weight, scaling the weights from 0 to 1. The σ_d values shown below each plot represent the range over which the normalized weighting functions result in a domain kernel with a radius of 1 (lower bound) to a radius of 20 (upper bound) after normalization and thresholding of values smaller than 0.01. The Average function is the Flat function with σ_r = ∞. Variables: x, the distance from zero in units of the voxel size (domain weighting) or in HU (range weighting); σ, σ_d (domain weighting) or σ_r (range weighting).

Given a pair of domain and range weighting functions and using the space-tonal normalized convolution expression of van den Boomgaard and van de Weijer[6], BF proceeds as follows:

$$\frac{\begin{array}{c}\int \mathrm{f}\left(\mathrm{y}\right)\mathrm{v}\left(\mathrm{x}\text{-}\mathrm{y}\right)\mathrm{w}\left(\mathrm{f}\left(\mathrm{x}\right)\text{-}\mathrm{f}\left(\mathrm{y}\right)\right)\mathrm{dy}\hfill \\ {\mathrm{R}}^{\mathrm{d}}\hfill \end{array}}{\begin{array}{c}\int \mathrm{v}\left(\mathrm{x}\text{-}\mathrm{y}\right)\mathrm{w}\left(\mathrm{f}\left(\mathrm{x}\right)\text{-}\mathrm{f}\left(\mathrm{y}\right)\right)\mathrm{dy}\hfill \\ {\mathrm{R}}^{\mathrm{d}}\hfill \end{array}}$$ (1)

where f() represents intensities, v() computes domain weights, w() computes range weights, and where d is the dimensionality of the data being filtered. In practice, equation 1 is discretized to voxel coordinates and an upper limit is placed on the spatial extent of the domain. In the work performed here, the domain weights were thresholded at 99% probability density (i.e. domain weights less than 1% were set to zero) and the kernel sizes were determined by the smallest cube which held all non-zero domain weights. Given this criterion, the σ values for the domain weighting functions (σ_d) were restricted to a range on which the minimum deviation yielded a kernel radius of 1 (a kernel size of 3) and the maximum deviation yielded a kernel radius of 20 (a kernel size of 41). Kernels with a radius larger than 20 were considered computationally impractical. The appropriate σ_d ranges for each weighting function are reported in Figure 1. No restrictions were placed on the standard deviation of the range weighting functions (σ_r).

Three forms of BF were investigated: classic BF (cBF), median-centric BF (mBF), and hybrid BF (hBF). As previously introduced, cBF is the product of domain and range weights with the range weights centered on the intensity of the voxel at the domain's geometric center. If the intensity of the central voxel contains noise, however, the range weighting is biased; mBF addresses this problem by centering the range weights on the median intensity within the domain (after thresholding). Unfortunately, mBF with a large kernel size introduces median filtration artifacts, filling in narrow features with neighboring intensities. Our hybrid filter, hBF, attempts to address the shortcomings of both cBF and mBF. Given a voxel to filter, hBF first performs a median filter using a Flat domain with a radius of one voxel. The radius of this median filter is not varied. The domain and range weighting of the BF can then be optimized as in cBF, independent from the median filter which estimates a center point for range-weighting. This hybrid ensures that only the narrowest features are compromised by median filtration artifacts (features which are generally difficult to differentiate from noise in the first place) while eliminating some degree of range-weighting bias.

To determine the optimal BF for smoothing 4D cardiac micro-CT data, BF performance was first optimized in 3D. Range-weighting is independent of dimensionality. For domain weighting, BF in 3D is a direct extension of BF in 2D because the third dimension is an additional spatial dimension. Adding a fourth dimension to the domain, time, required special considerations. When producing domain kernels for 4D BF, space and time were considered equivalent with 1 unit of the voxel size separating neighboring voxels in space and separating the same voxel at different points in time. For computational tractability, the time domain was limited to the cardiac phases immediately preceding and following the phase being filtered. For 4D hBF, the median filtration kernel was extended to 4D via duplication between time points rather than in accordance with space-time equivalence (see 3.2 4D Bilateral Filtration).

2.1 Simulations

Simulations were performed using the 4D MOBY mouse phantom[7]. The intensity of the phantom's blood was modified to be ~300 HU greater than the intensity of soft tissue, similar to the enhancement obtained with in vivo blood pool contrast agents such as Fenestra VC (ART, Saint-Laurent, Quebec). Nine 3D volumes were generated corresponding to cyclic cardiac phases. Each phase (256³; 100 μm isotropic voxels) was used to create 225 virtual projections, replicating the logistics of our custom micro-CT system[8]. Reconstruction was performed with the Feldkamp algorithm[9] using projections with and without Poisson noise. Poisson noise was added with MATLAB's imnoise function (The MathWorks, Natick, MA) and resulted in a realistic level of noise within the blood of the reconstructed data (stdev. ~ 65 HU).

2.2 BF Optimization

To optimize the performance of the 4D BF in the MOBY phantom, all possible domain and range combinations of the previously described weighting functions were first tested in 3D. Observations from these brute-force experiments were then used to simplify the 4D optimization process. 3D filtration was performed using one transverse slice from phase 3 of the MOBY phantom and up to 20 neighboring slices before and after the slice being filtered (to accommodate domain kernels with a radius up to 20). After filtration with each combination, the filtered slices were compared against the same slice from the original phantom (before projection and reconstruction) using the peak signal-to-noise ratio (PSNR) computed as follows:

$$\text{Root Mean Square Error}\left(\mathrm{RMSE}\right)=\sqrt{\frac{1}{{\mathrm{N}}_{\mathrm{V}}}\sum _{\mathrm{i},\mathrm{j}}{(\mathrm{f}(\mathrm{i},\mathrm{j})-\mathrm{b}(\mathrm{i},\mathrm{j}))}^2}$$ (2)

$$\mathrm{PSNR}=20{\text{log}}_{10}\left(\frac{1408.49}{\mathrm{RMSE}}\right)$$ (3)

where N_v is the number of voxels in the 2D slice being filtered, f() represents intensities in the phantom, b() represents intensities in the filtered slice, and where 1408.49 is the intensity range of the phantom.

Brute-force optimization of 3D BF was conducted once using cBF and once using mBF. For each combination, the domain (σ_d) was computed at 20 increments between and including the lower and upper bounds (Figure 1). This tested domain kernels with each radius from 1 and 20. The range (σ_r) was sampled every 8 HU until a bounded global maximum was found. Because the same domain and range combinations were found optimal for cBF and mBF (Flat domain, Flat range and Flat domain, Gaussian Range) and because hBF is a combination of these two filters, brute-force optimization of hBF was conducted using these combinations only. Brute-force optimization of 4D BF was also conducted using these combinations only.

2.3 In Vivo Validation

The optimal BF filters, as determined in the MOBY phantom, were applied to 4D cardiac micro-CT data collected from a C57BL/6 mouse (Charles-River, Wilmington, MA; male, 12 weeks of age, 28.5g weight). It was anesthetized with a mixture of 1.5% isoflurane, 50% oxygen, and 48.5% nitrogen delivered through a nose cone. The ECG signal was monitored with electrodes (Blue Sensor, Medicotest, UK) taped to the footpads, and body temperature was maintained using heat lamps, a rectal probe, and a feedback controller (Digi-Sense®, Cole Parmer, Chicago, IL). A pneumatic pillow on the thorax was used to monitor breathing. All physiological signals were processed with Coulbourn modules (Coulbourn Instruments, Allentown, PA) and recorded using a custom-written LabVIEW application (National Instruments, Austin, TX). An intravascular catheter (24 ga, BD Medical Systems, UT) was inserted in the lateral tail vein to inject a liposomal blood pool contrast agent[10] (contains 135 mg Iodine/ml; 0.01 ml/g mouse injected). For imaging, the animal was placed in an acrylic cradle containing the nose cone, an upper incisor clamp, and the pneumatic pillow[11]. The cradle assembly was seated vertically on the base of an angular stepper motor. X-ray projections were acquired with one chain of our dual source/detector micro-CT system[8]. 342 projections were acquired per phase for a total scanning time of 40 minutes per mouse (4 minutes/phase, 10 phases). Scanning parameters included a peak voltage of 80 kVp, a current of 125 mA, and an exposure of 10 ms/projection. Imaging was gated prospectively at the coincidence of end-expiration and the appropriate 10% increment of the R-R interval[12] (first 10% phase 1, second 10% phase 2, etc.). Phases were acquired consecutively, with phases 1 and 5 representing ventricular diastole and systole, respectively. Reconstruction was performed with the Feldkamp (FDK) algorithm[9] and Parker weighting[13] as implemented in the software package COBRA (Exxim Computing Corp., Livermore, CA). Each phase was reconstructed as a 512³ matrix of isotropic, 88 μm voxels. The total radiation was 0.7 Gy. This animal study was approved by the Duke University Institutional Animal Care and Use Committee.

Before performing BF on the in vivo data, all phases were affine registered to phase 1 using ANTs, an open-source ITK-based registration toolkit (http://picsl.upenn.edu/ANTS/). This registration compensated for small-scale motion of the mouse over the course of the 40 minute acquisition process. Affine registration was not performed on the phases of the MOBY phantom because the phases of the MOBY phantom are innately registered.

2.4 Computation

Numerous methods exist for speeding up computation of BFs (ex. CPU and GPU-based parallelization). For simplicity, such methods were excluded from this work, and, as such, the computation times reported here represent a baseline given the computer hardware used: a Macintosh workstation with two, 2.66 GHz quad-core Xenon processors and 16GB of RAM. Computation time was used as a criterion for selecting the optimal 3D BFs to be considered for 4D filtration, under the assumption that each domain and range combination would benefit equally from computational speed ups. All BFs were implemented using MATLAB (The MathWorks, Natick, MA).

3. RESULTS

3.1 3D Bilateral Filtration

Table 1 summarizes the top results (highest PSNRs) for the brute-force optimization of all possible combinations of the domain and range kernels for both cBF and mBF. The top 10 domain and range combinations for cBF are seen to yield significantly higher PSNRs than the noisy and noiseless reconstructions as well as all mean and median filters, though the computation time for calculating the cBF results is more than double the computation time for the mean and median filters. While not in the top 10 combinations, the cBF of Tomasi and Manduchi^[1] is seen to compare favorably with the top 10 filters in terms of PSNR (Gaussian domain and range); however, the computation time for filters with a Gaussian domain is seen to be quite high (>20 seconds) because of the large optimal kernel size (21). The Flat domain, Flat range and Flat domain, Gaussian range combinations were chosen for optimization of the 4D cBF because of their compact kernel sizes and correspondingly fast computation times. While the second combination has a decidedly lower PSNR (31.45 vs. 31.67), its highly compact optimal domain and range made it worth further investigation. The top 10 results for mBF are seen to be less encouraging, with even the optimal combination (Flat range, Flat domain) resulting in a PSNR lower than the PSNR of the noiseless reconstruction (30.65 vs. 30.74); however, this optimal combination substantially outperforms the median filter at a comparable kernel size (30.65 vs. 29.33). Optimizing hBF using the domain and range combinations chosen as optimal for cBF and mBF, hBF is seen to yield significantly higher PSNRs for both combinations (31.67, cBF vs. 32.05, hBF for a Flat domain and range).

Table 1.

Optimal 3D Bilateral Filters

Type	Domain	Range	PSNR	Time (sec)	σ d	σr (HU)	Kernel Size
Noiseless Recon	-	-	30.74	-	-	-	-
Noisy Recon	-	-	25.74	-	-	-	-
Classic	Tukey	Flat	31.68	14.26	8.44	228.42	17
	Cos	Flat	31.68	11.32	7.05	236.26	15
	AW	Flat	31.67	14.30	8.09	228.42	17
	Gauss	Flat	31.67	23.81	3.30	228.42	21
	Flat	Flat	31.67	8.92	6.00	228.42	13
	Lor	Flat	31.60	23.90	0.72	228.42	21
	EFF	Flat	31.52	14.26	0.09	228.42	17
	HMM	Flat	31.52	18.05	0.09	228.42	19
	Flat	Gauss	31.45	8.45	6.00	150.00	13
	Cos	Gauss	31.43	11.08	7.05	150.00	15
	Gauss	Gauss	31.42	29.44	3.30	150.00	21
Median-Centric	Flat	Flat	30.65	6.29	3.00	228.42	7
	Flat	Cos	30.63	6.47	3.00	322.53	7
	Flat	AW	30.62	7.12	3.00	338.21	7
	Flat	Tukey	30.61	6.21	3.00	369.58	7
	Flat	Gauss	30.54	5.53	3.00	142.16	7
	Cos	Flat	30.48	6.31	3.02	228.42	7
	AW	Flat	30.45	6.32	3.04	244.11	7
	Cos	Cos	30.44	6.53	3.02	322.53	7
	Cos	AW	30.43	7.19	3.02	338.21	7
	Cos	Tukey	30.42	6.20	3.02	369.58	7
Hybrid	Flat	Flat	32.05	12.83	7.00	212.74	15
	Flat	Gauss	31.92	12.45	7.00	134.32	15
Reference: Mean	Flat	Average	28.02	3.51	1.00	-	3
	Flat	Average	27.55	3.69	2.00	-	5
	Flat	Average	25.74	3.88	3.00	-	7
	Flat	Average	24.58	4.32	4.00	-	9
Reference: Median	Flat	Average	28.17	1.90	1.00	-	3
	Flat	Average	29.53	2.17	2.00	-	5
	Flat	Average	29.33	2.67	3.00	-	7
	Flat	Average	28.63	3.58	4.00	-	9

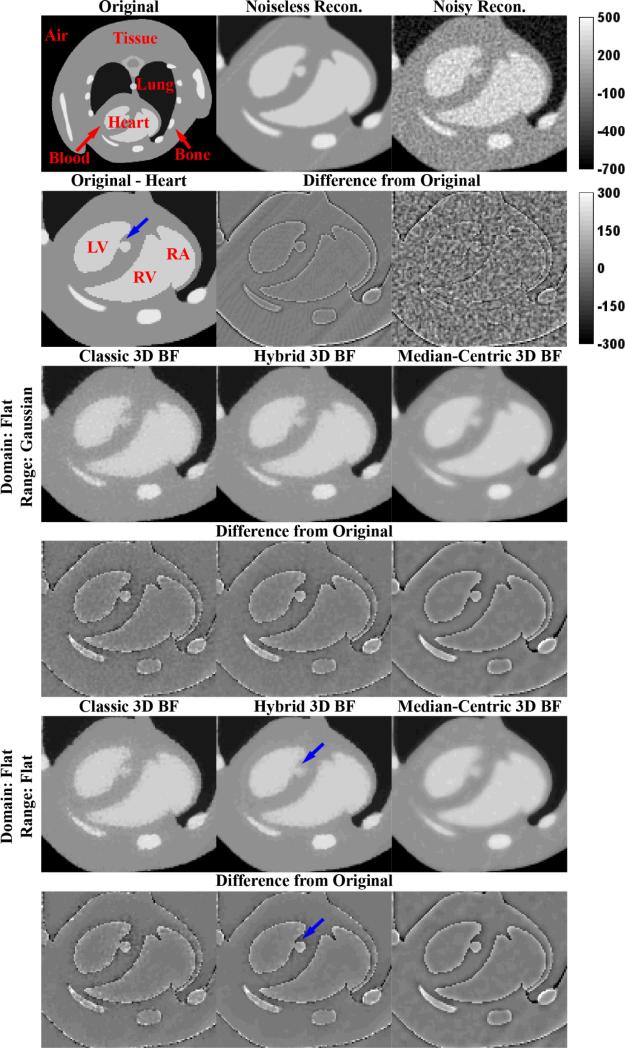
The results of applying the optimal filters from Table 1 (highlighted in yellow) to a transverse slice through phase 3 of the MOBY phantom are summarized in Figure 2. While the “Original” image shows the complete slice used for PSNR calculations, in the interest of comparisons with 4D filtration results, all filtration results are zoomed in to the “Heart” portion of the slice which changes between phases. For reference, Figure 2 also illustrates what the phantom looks like when reconstructed with the Feldkamp algorithm (“Noiseless Recon.”) and when reconstructed with the Feldkamp algorithm after the introduction of noise (“Noisy Recon.”). Because all PSNRs were calculated in reference to the “Original” phantom and not the “Noiseless Recon.”, a higher PSNR illustrates not only the ability to preserve edges in the phantom, but the ability to smooth reconstruction artifacts as well (artifacts seen most clearly in the “Noiseless Recon.” difference image). For both domain and range combinations, the cBF results are seen to do an excellent job of preserving edges; however, the edges remain quite noisy. The mBF results provide more consistent smoothing at edges, but median filtration artifacts are seen to adversely affect narrow features. The hBF results are seen to provide a compromise between edge preservation and smoothing while most accurately smoothing larger regions of constant intensity (e.g. the left ventricle).

Figure 2. Optimal 3D Bilateral Filters.

Application of the optimal 3D BFs (Table 1, highlighted in yellow) to a slice of phase 3 of the MOBY phantom reconstructed with noise (“Noisy Recon.”). Red labels highlight anatomic structures: LV, left ventricle; RV, right ventricle; RA, right atrium. Blue arrows denote a point of interest referenced in the text. The top intensity calibration bar applies to all grayscale images. The bottom intensity calibration bar applies to all difference images. All intensities are reported in HU.

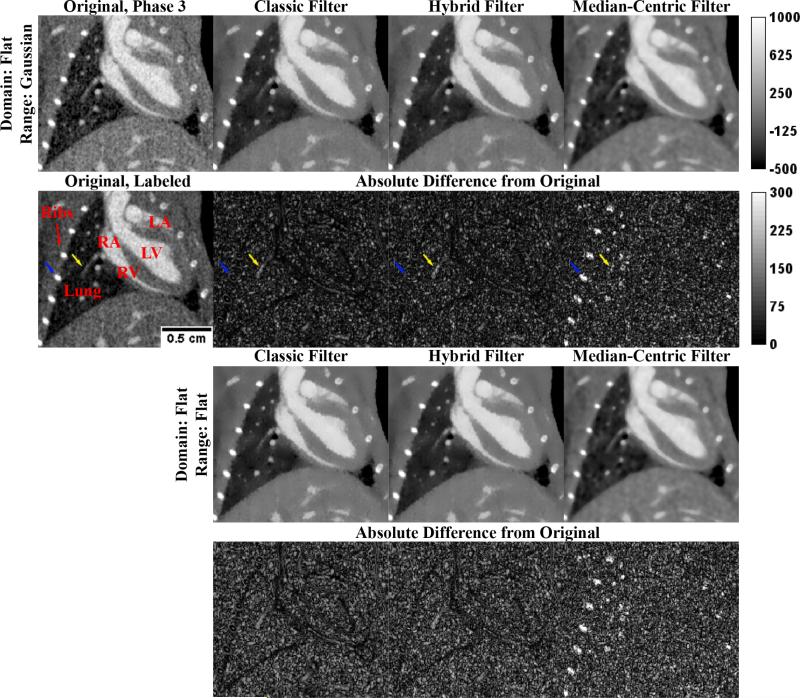
Figure 3 summarizes the results of applying these optimal 3D filters to a slice from phase 3 of the in vivo data. Relative filter performance is seen to closely mirror performance in the MOBY phantom. Blue arrows highlight a rib which is highly over smoothed by mBF. Yellow arrows indicate a blood vessel in the lung which is noticeably attenuated by both cBF and hBF. Using cBF, high contrast intensity boundaries (such as those between the heart and the lung) are black, indicating limited smoothing. This problem is seen to be less significant when using hBF, particularly when the Flat domain and range are used. To measure the degree of smoothing in large, constant regions, the standard deviation of the blood within the left ventricle was measured within the filtered slice, a region where the true standard deviation is assumed to be very close to zero. Results for the Flat domain and Gaussian range combination were as follows (filter, stdev.): original, 72.24 HU; cBF, 25.78 HU; mBF, 29.24 HU; hBF, 23.37 HU. Slightly smoother results were obtained for the Flat domain and Flat range combination: cBF, 23.72 HU; mBF, 29.07 HU; hBF, 20.52 HU. As in the MOBY phantom, hBF is seen to provide the most dramatic smoothing in constant regions.

Figure 3. Application of the Optimal 3D Bilateral Filters to In Vivo Data.

Application of the optimal 3D BFs (Table 1, highlighted in yellow) to a slice of the in vivo data (“Original, Phase 3”). Red labels highlight anatomic structures: LV, left ventricle; RV, right ventricle; LA, left atrium; RA, right atrium. Blue and yellow arrows denote points of interest referenced in the text. The scale bar on “Original, Labeled” applies to all images. The top intensity calibration bar applies to all grayscale images. The bottom intensity calibration bar applies to all difference images. All intensities are reported in HU.

3.2 4D Bilateral Filtration

Table 2 summarizes the performance of 4D BF using cBF, mBF, and hBF with the two previously selected domain and range combinations (Flat domain, Flat range; Flat domain, Gaussian range). The PSNRs, kernel sizes, and optimal σ_r values for cBF are seen to remain largely unchanged, even though the computation time more than doubles from the analogous 3D filter. The optimal kernel sizes and σ_r values for mBF remain roughly the same, but the PSNRs are seen to increase dramatically (31.58 vs. 30.65 for a Flat domain and range). Thanks to the compact kernel size, computation times for 4D mBF remain manageable (<11 seconds).

Table 2.

Optimal 4D Bilateral Filters

Type	Domain	Range	PSNR	Time (sec)	σ d	σr (HU)	Kernel Size
Classic	Flat	Flat	31.69	21.72	6.00	228.42	13
	Flat	Gauss	31.46	21.03	6.00	150.00	13
Median-Centric	Flat	Flat	31.58	10.56	3.00	220.58	7
	Flat	Gauss	31.40	10.51	3.00	134.32	7
Hybrid	Flat	Flat	32.25	35.49	8.00	197.05	17
	Flat	Gauss	32.19	42.17	9.00	118.63	19
Reference: Mean	Flat	Average	28.53	4.37	1.00	-	3
	Flat	Average	27.77	4.74	2.00	-	5
	Flat	Average	25.99	5.57	3.00	-	7
	Flat	Average	24.56	6.61	4.00	-	9
Reference: Median	Flat	Average	28.69	3.19	1.00	-	3
	Flat	Average	29.88	3.87	2.00	-	5
	Flat	Average	29.50	5.59	3.00	-	7
	Flat	Average	28.64	8.71	4.00	-	9

As previously mentioned, the results reported in Table 2 for hBF do not represent a direct, 4D extension of hBF as they do for cBF and mBF. Directly extending hBF to 4D while maintaining the one voxel radius for the median filter used to center the range weights would only include one voxel from each neighboring phase within the median filter. In practice, this did not have a meaningful impact on hBF performance (did not change the PSNR results). Therefore, hBF was instead extended to 4D by duplicating the median filtration kernel to the neighboring phases, considering 6 additional voxels from each neighboring phase instead of just 1. In terms of PSNR, this modification resulted in a noticeable improvement of 4D hBF performance over 3D hBF (32.05, 3D vs. 32.25, 4D for a Flat domain and range); unfortunately, this modification and an increased optimal kernel size approximately tripled the computation times for both domain and range combinations.

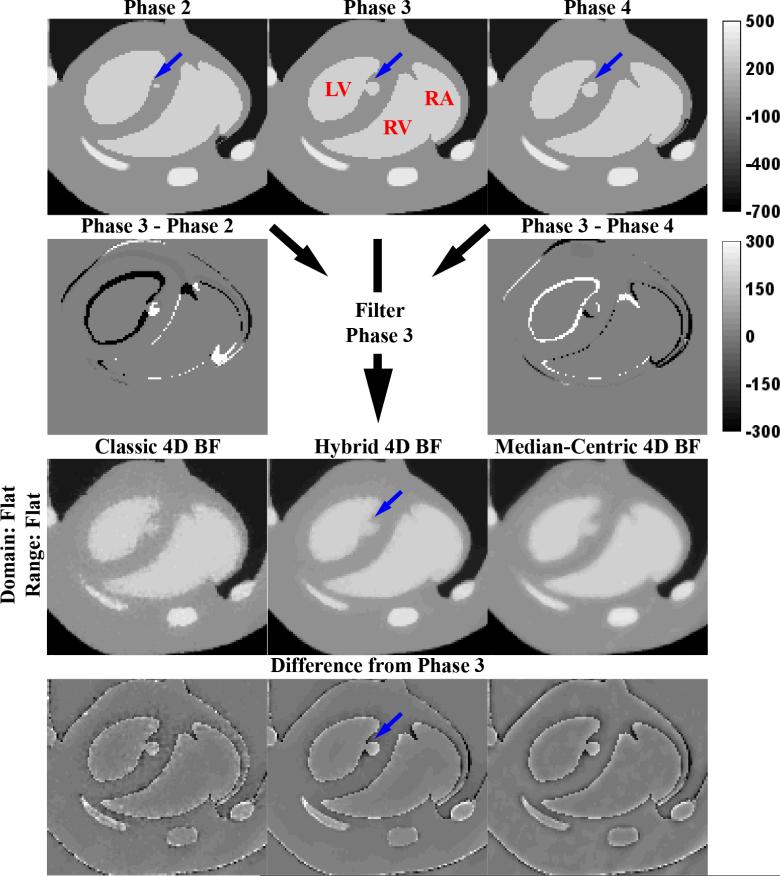
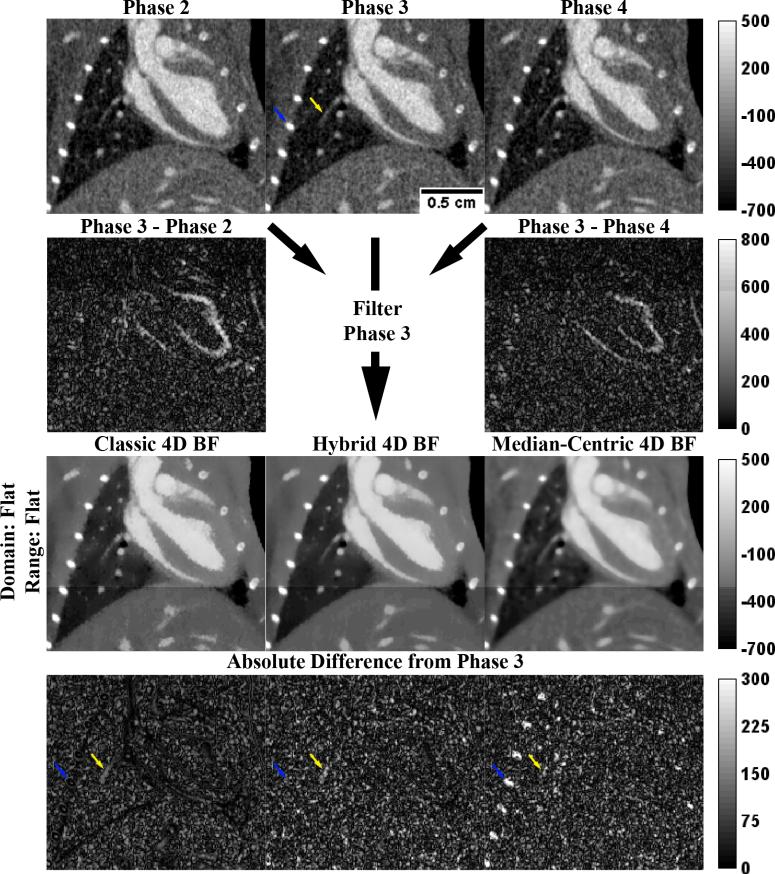
Figure 4 illustrates the performance of 4D cBF, mBF, and hBF. Corresponding slices (from the original phantom) are shown for phases 2, 3, and 4, all of which are used to filter the “Noisy Recon.” slice from phase 3 (Figure 2). Difference images between phases illustrate how the lungs and heart change over time. Consistent with the changes in the optimal PSNRs see when moving from 3D BF (Table 1) to 4D BF (Table 2), performance of the cBF remains largely unchanged. The increase in PSNR for mBF can be largely attributed to better smoothing in constant regions such as the left ventricle; however, median filtration artifacts around the heart are exacerbated by inclusion of neighboring phases within the filtering kernel. Extending hBF by duplication instead of direct extension is seen to introduce more severe median filtration artifacts into the hBF results (see blue arrows, compare with analogous blue arrows in Figure 2); however, this change is also seen to improve smoothing at the boundaries between the cardiac chambers and surrounding myocardium.

Figure 4. Optimal 4D Bilateral Filters.

Application of the optimal 4D BFs (Table 2, highlighted in yellow) to a slice of phase 3 of the MOBY phantom reconstructed with noise (“Noisy Recon.” From Figure 2). For 4D BF, the filtering kernel expands to the phases before and after (phases 2 and 4, respectively) the phase being filtered (phase 3). Red labels highlight anatomic structures: LV, left ventricle; RV, right ventricle; RA, right atrium. Blue arrows denote a point of interest referenced in the text. The top intensity calibration bar applies to all grayscale images. The bottom intensity calibration bar applies to all difference images. All intensities are reported in HU.

These observations carry over to the in vivo data in Figure 5. Visually, the 4D cBF and mBF results are very similar to the 3D cBF and mBF results from Figure 3. Owing to the modification made to the median filter used for 4D hBF, smoothing is seen to be more consistent at edges than it was for 3D hBF. The blue and yellow arrows (at the same anatomic potions as in Figure 3) illustrate that the treatment of ribs and the blood vessel within the lung remain largely unchanged between 3D BF and 4D BF. All 4D BFs are seen to more greatly smooth the blood within the left ventricle than their 3D counterparts (filter, stdev.): original, 72.24 HU; cBF 20.30 HU, mBF 24.14 HU, hBF 15.91 HU (Flat domain and range).

Figure 5. Application of the Optimal 4D Bilateral Filters to In Vivo Data.

Application of the optimal 4D BFs (Table 2, highlighted in yellow) to a slice of the in vivo data (“Phase 3”). For 4D BF, the filtering kernel expands to the phases before and after (phases 2 and 4, respectively) the phase being filtered (phase 3). Anatomic labels have been excluded for clarity (see Figure 3). Blue and yellow arrows denote a point of interest referenced in the text. The scale bar on “Phase 3” applies to all images. Intensity calibration bars apply to all images in their respective rows. All intensities are reported in HU.

4. DISCUSSION AND CONCLUSIONS

The true information underlying noisy CT data is piecewise-smooth (to a very close approximation) because of the relatively low contrast sensitivity of CT. Under the hypothesis that BF provides an ideal framework for denoising piecewise-smooth data, the purpose of this work was to optimize BF performance for denoising 4D cardiac micro-CT data. In simulations, brute-force optimization of every combination of eight domain and range weighting functions was used to find optimal combinations for filtering the MOBY phantom in 3D using both cBF and mBF. A new BF, hBF was invented to address shortcomings in these results. These three BFs as well as two optimal domain and range weighting function combinations were then extended to 4D. All optimal 3D and 4D BFs were validated using in vivo, murine, 4D cardiac micro-CT data.

In both 3D and 4D, several characteristics of each type of BF became apparent. The cBF was seen to strongly preserve high-intensity edges; however, denoising performance was seen to suffer at edges, likely due to noise bias in the intensity on which the range weights were centered. Because the optimal 3D kernel was already quite large (13 voxel kernel size), extension of the kernel to 4D had very little impact on denoising performance (optimal PSNR of 31.69, 4D vs. 31.67, 3D for a Flat domain and range). In 3D, mBF was seen to introduce median filtration artifacts around narrow features, resulting in a comparatively low optimal PSNR of 30.65. Extension of mBF to 4D yielded a dramatic improvement in the optimal PSNR (31.58); however, this increase can be largely attributed to improved smoothing in constant regions (in vivo left ventricle stdev. measurements: 29.07 HU, 3D vs. 24.14 HU, 4D). In spite of this increase in PSNR, the introduction of median filtration artifacts around the heart appeared similar, or possibly worse, when moving from 3D mBF to 4D mBF. In both 3D and 4D, hBF was seen to outperform both cBF and mBF in terms of optimal PSNR (32.05, 3D; 32.25, 4D). In 3D, this superior PSNR resulted from a compromise between the edge-sensitivity of cBF and the median filtration inherent in mBF. Surprisingly, the ability of 3D hBF to smooth constant regions was found to be superior to both cBF and mBF (in vivo left ventricle stdev. measurements: cBF, 23.72 HU; mBF, 29.07 HU; hBF, 20.52 HU), an ideal characteristic for filtering piece-wise smooth CT, particularly for applications such as dose reduction. This property was even more dramatic for 4D hBF (cBF 20.30 HU, mBF 24.14 HU, hBF 15.91 HU); however, the modifications made to hBF in extending it to 4D made it prone to the median filtration artifacts of 4D mBF (Figure 4, blue arrows).

Of all filters tested, it is clear that 3D hBF with Flat domain and range weighting functions provides optimal denoising results while minimizing potential filtration artifacts. Its performance comes with a proportional increase in computation time (from Table 1: 8.92 sec., cBF; 6.29 sec., mBF; 12.83 sec. hBF). Even if the exorbitant computation time of 4D hBF could be overcome (from Table 2: 21.72 sec., cBF; 10.56 sec., mBF; 35.49 sec. hBF), the risk of introducing heterogeneous median filtration artifacts between cardiac phases is too great when optimizing BF explicitly for cardiac studies. Therefore, of the 3D and 4D BF variants investigated, 3D hBF with Flat domain and range weighting functions is recommended for denoising 4D cardiac micro-CT data. This conclusion is particularly appealing because 3D BF performance is independent of the registration between phases. Furthermore, because the optimal filter's performance is not specifically tailored to provide optimal results for the heart, 3D hBF should denoise the lungs and other anatomic features of interest similarly well.