DrML: Probabilistic Modeling of Gene Duplications

Abstract

DrML is a software program for inferring evolutionary scenarios from a gene tree and a species tree with speciation time estimates that is based on a general maximum likelihood model. The program implements novel algorithms that efficiently infer most likely scenarios of gene duplication and loss events. Our comparative studies suggest that the general maximum likelihood model provides more credible estimates than standard parsimony reconciliation, especially when speciation times differ significantly. DrML is an open source project written in Python, and along with an on-line manual and sample data sets publicly available.

1. Introduction

Gene duplication and subsequent loss are a fundamental genomic process for acquiring new genetic function and therefore, adaptive innovations. Biologists have long acknowledged that there are extensive variations in evolutionary scenarios of gene duplication events among species, and, consequently, such events play a critical part in many evolutionary studies. Gene tree reconciliation problems have been traditionally used to infer evolutionary scenarios, and are based on the observation that duplication and loss events leave traces of discordance between their evolutionary history and the species tree along whose branches they evolve. However, the specific reconciliation problem taken to infer evolutionary scenarios will have critical impact on the successful estimation of meaningful phylogenetic relationships. A classical reconciliation problem is parsimony reconciliation that, given a gene tree and a species tree, seeks the evolutionary scenario with the minimum number of gene duplications and losses necessary to reconcile the discordance between the gene tree and the species tree. Although this problem has produced several credible estimates (Akerborg et al., 2009; Doyon et al., 2009), and exact solutions can be computed in linear time (Zhang, 1997), it is based on an overly simplistic model that is prone to failure in practice (Doyon et al., 2009) (e.g., when the divergence times of the species tree differ significantly). More recently, probabilistic reconciliation problems for estimating gene duplication and loss scenarios have been introduced and potentially can overcome limitations of the basic reconciliation problem. These problems can be solved efficiently by using exact algorithms (Górecki et al., 2011).

We introduce DrML, a software program that implies gene duplication and loss scenarios from a general maximum likelihood (ML) reconciliation model for a given gene tree and species tree with branch lengths (Fig. 1). To efficiently compute such scenarios, DrML implements, for the first time, the technically complex algorithms described previously (Górecki et al., 2011). Our run-time analyses demonstrate that DrML is able to compute large-scale studies of gene duplication and loss scenarios. Finally, our empirical studies using DrML suggest that the general ML model implies more credible evolutionary scenarios than the standard parsimony reconciliation.

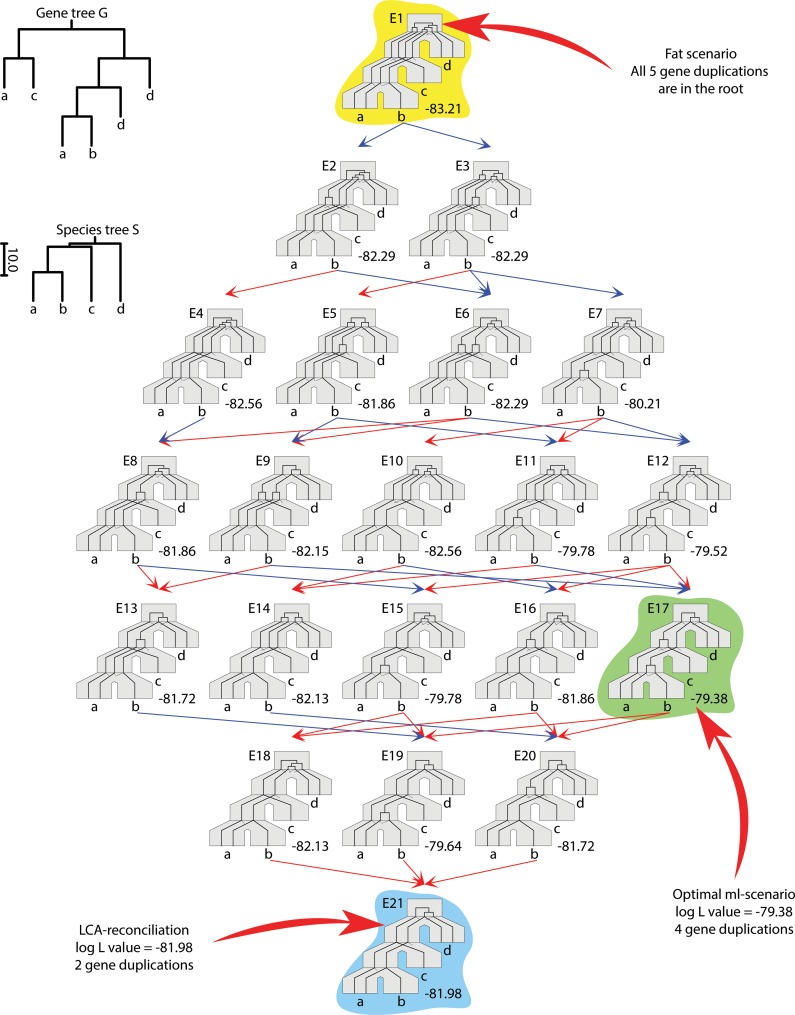
FIG. 1.

A gene tree G = ((a,c), (((a,b),d),d)) and a species tree S = (((a : 9, b : 9) : 8,c : 17) : 1,d : 18) : 2 with evolutionary scenarios (embeddings) in the duplication-loss model are depicted as a reduction diagram (for more details, see Górecki and Tiuryn, 2006). The log L values are computed for λ = 1.3. The most likely evolutionary scenario is E17 (log L = −78.38). DrML can compute this value as well as the optimal DLS tree(s). Additionally, DrML computes the number of gene duplications and log L values for the lca scenario (the minimal scenario in the duplication-loss model; see the bottom embedding E21) and for the fat scenario (the scenario having all possible gene duplications in the root of the species tree; see the top embedding E1).

1.1. Related work

Goodman et al.'s pioneering work (Goodman et al., 1979; see also Page, 1994) introduced a parsimony model for reconciling a gene tree with a species tree, where both trees are rooted and binary. In this model, the gene tree is embedded into the species tree by the least common ancestor (lca) mapping. The mapping relates every gene in the gene tree to the most recent species that could have contained the gene. In particular, every leaf of the gene tree is mapped to the leaf of the species tree representing the species from which it was sampled. The resulting embedding represents an evolutionary scenario of gene duplication and loss events. Genes that are embedded into the same species as one of their children are gene duplications, and maximum subtrees in the species tree without an embedding are losses. Although there are many other evolutionary scenarios possible (e.g., where some genes are mapped to proper ancestors of their lca mappings), the lca-based evolutionary scenario is the most parsimonious one in the number of gene duplication and loss events (Bonizzoni et al., 2005; Górecki and Tiuryn, 2006). Therefore, this model is referred to as the parsimony reconciliation model. Evolutionary scenarios under this model can be computed efficiently by algorithms that are implemented in various software packages (Górecki and Tiuryn, 2007; Chaudhary et al., 2010), and despite its simplicity appear to have produced some credible evolutionary studies for small rates of gene duplication and loss events (e.g., Page, 2000; Page and Cotton, 2002; Martin and Burg, 2002; Sanderson and McMahon, 2007). Subsequent programs based on variations of the parsimony model have attempted to improve biological realism (e.g., error correction of the given trees and unrooted gene trees) (Chaudhary et al., 2012; Dondi and El-Mabrouk, 2012; Górecki and Eulenstein, 2012). Moreover, many higher level approaches in evolutionary biology are based on this model, which includes the estimation of gene duplication episodes (e.g., Bansal and Eulenstein, 2008; Burleigh et al., 2009) and supertree inference (e.g., Wehe et al., 2008). For further background, the interested reader may wish to consult Eulenstein et al. (2010).

However, the parsimony model might be often too restrictive and ignore many reasonable evolutionary scenarios of gene duplication and loss events that are not inferred from the lca mappings. For example, the model often discards evolutionary scenarios of genes that evolve with rapid rates of gene duplication and loss events, and several of such genes are biologically appealing like the MHC gene family (e.g., Slade et al., 1994), the olfactory receptor genes (e.g., Xiao et al., 2011), and the rhodopsin genes (e.g., Sugawara et al., 2002). To make matters worse, the parsimony model does not consider evolutionary time that is usually represented as edge lengths in the species tree, and a gene duplication may occur more likely on an edge that represents 100 million years than on an edge representing a fraction of this time. Although probabilistic models for reconciling gene trees have largely focused on birth–death processes, they represent only a narrow range of potential models, and reconciliation problems based on these models are computationally complex or prohibitive (Arvestad et al., 2004, 2009; Akerborg et al., 2009; Doyon et al., 2010). Only recently, a novel algorithm has been described that efficiently implies evolutionary scenarios from the general ML model for gene tree reconciliation by solving the ML reconciliation problem (Górecki et al., 2011). This model infers evolutionary scenarios of gene duplication and loss events from a gene tree and a species tree with branch lengths. The branch lengths in the species tree represent the time between neighboring speciation events, which can be inferred from molecular branch lengths and fossil calibrations. An effective way to model the gene duplication process is with a Poisson distribution, which assumes a constant average rate of duplications that is frequently used to model gene mutations. However, the duplication rate may vary among evolutionary lineages (Friedman and Hughes, 2001). Therefore, the model allows the use of any discrete distribution to model gene duplications throughout the species tree. More precisely, it can be assumed that for every branch of the species tree there is a given discrete distribution, which is parameterized by its length that defines the probability of having n gene duplications on this branch. Based on this model, the ML reconciliation problem is defined as follows: Given a gene tree and a species tree with branch lengths, find the evolutionary scenario of the gene duplications that is most likely under the ML model. Although this reconciliation problem is complicated by the inherently complex structure of the solution space of all evolutionary scenarios (Górecki and Tiuryn, 2006), algorithms that are based on the theory of DLS trees can efficiently address the problem (Górecki and Tiuryn, 2006).

1.2. Contribution

We introduce DrML, an efficient software program that enables, for the first time, analyses of evolutionary scenarios for gene duplications and losses by solving the ML reconciliation problem. In our test data sets, DrML identifies optimal ML scenarios within minutes, even when the gene trees contain sequences from several hundred species. In many cases, these scenarios appear to be much more realistic than scenarios that are inferred using standard parsimony-based reconciliation. We also present advanced application of DrML that allows verification of evolutionary hypotheses of gene duplication events in a given gene family. In our empirical example, we demonstrate how to analyze the ML scenarios of bootstrap gene trees inferred from the set of DNA repair XRCC4 proteins from 15 animal and two plant genomes.

2. Methods

2.1. Overview of the model

Here we give a brief description of the model of DLS trees (Górecki and Tiuryn, 2006) that is used by DrML to represent evolutionary scenarios, or reconciliations. Please refer to Górecki and Tiuryn (2006) for more details on the model of DLS trees.

A DLS tree is a binary tree with two types of internal nodes, denoting gene duplications and speciations, and two types of leaves, denoting gene losses and gene sequences. DrML uses the standard nested parenthesis notation adequately adopted to represent scenarios in the duplication-loss model. By C(T) we denote the set of species names present in a scenario T. The following rules define reconciliations:

• • a is a single-noded reconciliation denoting a gene sequence from species a.

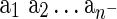• •  is a single-noded reconciliation denoting a lost gene lineage, where 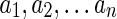is a non-empty list of species names; note that .

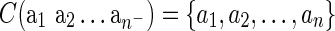• • (R₁, R₂)+ is a scenario whose root is a duplication node and its children are reconciliations R₁ and R₂ satisfying C(R₁) = C(R₂).

• • (R₁, R₂)∼ is a scenario whose root represents a speciation and its children are reconciliations R₁ and R₂ such that C(R₁) ∩ C(R₂) = ∅.

For example, ((x, y)∼, x y−)+ is a valid reconciliation in which one copy of a gene is immediately lost after a duplication event. Note that (a−, (a, b)∼)+ does not represent any scenario. The lca scenario depicted in Figure 2 has the following representation:

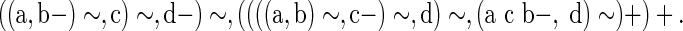FIG. 2.

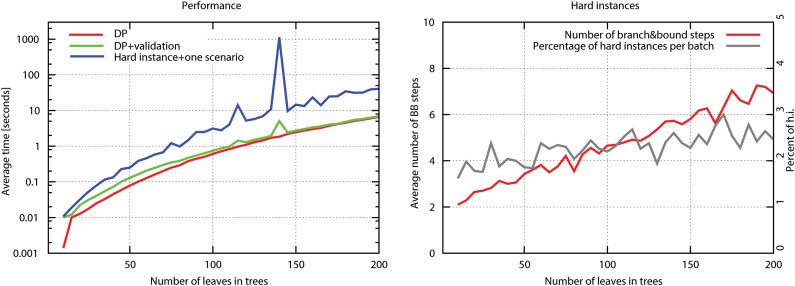
Performance of DrML. (Left diagram) The performance of the main phases of DrML for randomly generated instances of uniquely labeled gene and species trees with the same set of leaf labels: DP (option −dm) - computing log L value by the dynamic programming algorithm; DP + validation (option −dr) - inferring optimal scenarios for non-hard instances, and full (option −dh). (Right diagram) The percentage of hard instances with the average number of branch and bound steps required to resolve a given hard instance. The values on the x-axis denote the number of leaves in a single tree.

In general, it is rather straightforward to infer duplication and speciation nodes in a valid scenario, and therefore, + and ∼ can be omitted. For example, the latter scenario can be rewritten in the following way:

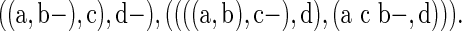Let S be a rooted species tree with branch lengths. For a node 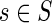we denote by |s| the length of the branch connecting s with its parent in S. Let P(τ,d|λ) denote the probability that d duplications occurred during the time period τ under the assumption of a constant duplication rate λ. Without loss of generality, we use the Poisson distribution:

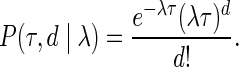The likelihood of a given reconciliation R of a species tree S and a gene tree G is defined by:

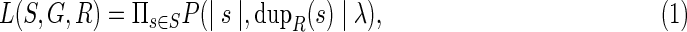where dup_R(s) is the number of gene duplication events associated with the species s in the reconciliation R. Given a species tree S with branch lengths and a gene tree G, we call the reconciliation R optimal if it maximizes the likelihood L(S,G,R) in the set of all reconciliations of S and G.

One of the most important problems that is solved by our software program is the inference of an optimal reconciliation for a given species tree S and a gene tree G. An instance of this problem with optimal solution is depicted in Figure 2.

2.2. Description of the software

DrML is a software program written in Python 2.7. It consists of several scripts to support M analyses of evolutionary scenarios under the gene duplication model. The effective algorithms from Górecki et al. (2011) are implemented in the main script drml.py. In particular, this script can be used to solve the problem of the optimal reconciliation inference.

DrML has a simple command line interface. Input trees can be defined by several options: −s TREE a rooted species tree with branch lengths, −g TREE a rooted gene tree, or −p FILE a file that contains a pair of trees separated by the newline (EOLN) character. The duplication rate, that is, λ parameter in Poisson distribution (1), can be set by −L option. The default value of λ is set to 0.005.

Given an instance of a rooted species tree S with branch lengths and a rooted gene tree G, DrML can infer one or all optimal ML reconciliations of G and S. Although in practice DrML can compute most instances of the problem efficiently, there are a few instances, called hard instances, that require more time to compute (Górecki et al., 2011).

For example, for random gene and species trees, when the gene tree is larger than the species tree, only 0.2% of the instances of the problem are hard (Górecki et al., 2011). For the trees with unique leaf labeling and the same size, the ratio is approximately 2% (see Section 3 for more details). Consequently, DrML implements several algorithms for processing hard and non-hard instances:

• • DP - a dynamic programming algorithm for computing the log L value only. ML values computed by the DP algorithm will be incorrect if the input instance is hard.

• • DP + validation - the DP algorithm with validation procedure that allows inference of optimal scenarios for non-hard instances. This algorithm detects hard instances.

• • Full - DP + validation and hard instance processing.

In summary, to initialize the ML analysis, the option −m should be provided. Additionally, the program can compute:

• • (DP) the likelihood of an optimal duplication-speciation setting value (option −dm); DP algorithm only without hard instance detection.

• • (DP + validation) one or all optimal reconciliations [options −dr (default) or −dra]; hard instances are detected, but optimal ML scenarios will be inferred only for non-hard instances.

• • (Full) one or all optimal reconciliations (options −dh or −dha); inference of optimal scenarios.

For example, the optimal scenario, with log-likelihood −79.38, from Figure 2 can be inferred by DrML by the following command line:

drml.py −m −L1.3 −g “((a,c),(((a,b),d),d))” −s “(((a:9,b:9):8,c:17):1,d:18):2”

An example of a hard instance processing is given below:

drml.py −m −dh−L1.0 −g “((a,c),((((b,c),c),c),d))”−s“(((a:9,b:2):8,c:3):1,d:13):2”

The log L score equals −37.712318 and the optimal reconciliation is:

((((a,b−),c),d−),((((((b,a−),c),(c,a b−)),(c,a b−)),d−),(d,a b c−))).

The main output file of DrML is drml.dls, which contains the input gene tree, the input species, and the set of optimal DLS trees. DrML can also read and analyze multiple dls files. For example, in our experiments we performed multiple runs of DrML using bootstrapped trees that were inferred from a given gene family. The following command line can be used to collect frequencies of events from many optimal scenarios inferred by DrML:

drml.py −Df *.dls

For instance, for the following input file (drml.dls) with three scenarios:

# gene tree

(a,(b,b))

# species tree

(a,b)

# scenarios

((a,b−)^∼,((a−,b)^∼,(a−,b)^∼)+)+

((a,b−)^∼,((b,b)+,a−)^∼)+

(a,(b,b)+)^∼

DrML will create file drml.freq.txt:

a b

+ {0: 1, 1: 1, 2: 1}

− {0: 3}

∼ {1: 1, 2: 1, 3: 1}

a

+ {0: 3}

− {0: 1, 1: 1, 2: 1}

∼ {1: 3}

b

+ {0: 1, 1: 2}

− {0: 1, 1: 2}

∼ {2: 3}

For each node in the species tree, denoted by its corresponding cluster, the numbers in brackets denote the frequency of a given event type. For example, the second line of the output describes the frequencies for the gene duplications (+) located in the root of the species tree. In particular, we have the following frequencies: (i) one scenario with no duplication in the root, (ii) one scenario with one duplication, and (iii) one scenario with two duplications in the root, and so on. Speciation frequencies (∼) for the leaves denote the number of genes. For example, in the last line, we have two genes from b for each scenario. An example of a species tree with histograms of event frequencies is depicted in Figure 3.

FIG. 3.

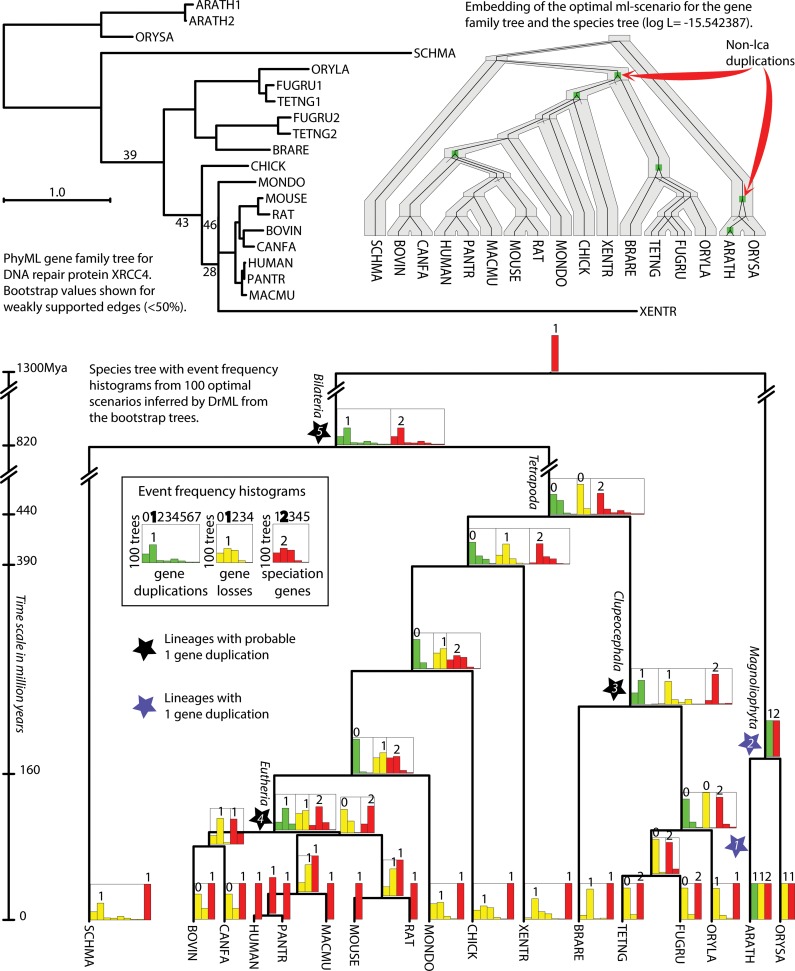
Gene duplication analysis by gene tree bootstrapping and using DrML. (Top left) PhyML gene tree for DNA repair proteins XRCC4 rooted by Urec (Górecki and Tiuryn, 2007). Bootstrap values for 100 samples are shown for the edges with the support less than 50%. (Top right) Embedding of the ML scenario inferred by DrML into the species tree (shown below). This optimal scenario has two more duplications than the lca scenario. These non-lca duplications are indicated by red arrows. The log L of the optimal scenario equals −15.542387 (−18.649822 for the lca scenario). (Bottom) The species tree with branch lengths proportional to time with event frequency histograms computed for the set of 100 optimal DrML scenarios inferred for the 100 bootstrap gene trees. For each edge of the species tree, we present three histograms showing the frequencies of given type of events. Each histogram has a number shown above the highest bar. This number denotes the most frequent number of events associated with a given edge among analyzed set of scenarios. Stars denote the edges where gene duplication events are the most likely.

Other options are described in the documentation included in the software package.

DrML is an open source project written in Python, with an on-line manual and sample data sets publicly available at http://bioputer.mimuw.edu.pl/gorecki/drml.

3. Experiments

3.1. Run-time analysis

We tested the performance of DrML with randomly generated species and gene trees generated by the software program Urec (Górecki and Tiuryn, 2007). For each 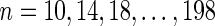, we randomly generated 10⁵ pairs of a species tree and a gene tree with n uniquely labeled leaves. The branch lengths of the species trees were sampled from a uniform distribution across the interval [1 … 20].

DrML performs well with the simulated data sets even for large trees with almost hundreds of leaves; the algorithm still finishes in less than 50 sec on average.

Hard instances occurred in only 2% of the simulated data sets (see Fig. 1), whereas most of the instances were solved by using 2–4 steps of the branch and bound algorithm. We observed the increase of random hard instances to 2% from 0.2% as tested by a preliminary prototype of DrML described previously (Górecki et al., 2011). The difference is caused by a different model of gene tree generation. Here, the gene trees have unique leaf labeling, whereas in the previous study (Górecki et al., 2011) for a species tree with size n, the gene tree was generated with 1.25 * n randomly labeled leaves.

In general, the current version of DrML is approximately 30% faster than its prototype (Górecki et al., 2011).

3.2. Empirical data set

We first obtained 20 gene sequences of DNA repair XRCC4 proteins from the TreeFam v8.0 database (Li et al., 2006; Ruan et al., 2008) (gene family id TF101204), and aligned them using the program MUSCLE (Edgar, 2004). Then, for the alignment, we performed an ML phylogenetic analysis with bootstrapping (100 samples) using PhyML version 20111216 (Guindon et al., 2009) with the default parameter setting. All ML analyses were used with the default program setting. To root the gene tree, we identified the rooting that minimizes the number of gene duplications and gene losses by using the program Urec (Górecki and Tiuryn, 2007). The rooted gene family tree is depicted in Figure 3, together with weakly supported edges determined by the bootstrap analysis.

We used a species tree generated from TreeFam (based on NCBI taxonomy), with the branch lengths obtained from diversification dates in the TreeTime database (Hedges et al., 2006). The species tree is depicted at the bottom of Figure 3 with branch lengths representing time.

For the analysis, we set the duplication rate (λ) to 0.005 following the estimated rate of gene duplication and loss in the vertebrate genome by Cotton and Page (2005).

The optimal scenario inferred by DrML has six gene duplications, which is two more than for the lca scenario. The log L value of the optimal scenario equals −15.542387, whereas for the lca scenario it is equal to −18.649822 (four gene duplications) and for the fat scenario −153.349489 (19 gene duplications).

First, we observe that a single optimal scenario might be insufficient to verify evolutionary hypotheses. As shown in the embedding (top right in Fig. 3), we have two non-lca duplications detected by DrML. Both duplications seem to be related to the long branches: ∼1,000 Mya for plant Magnoliophyta and ∼400 Mya for the Tetrapoda. The first duplication can be resolved by adding more genes from plant genomes. In general, both duplications require additional analysis, especially as the gene tree has four poorly supported edges. To resolve the problem, we perfomed multiple runs of DrML on 100 bootstrap trees inferred by PhyML from the multiple alignment of gene sequences from the input gene family. Then we computed the frequencies of evolutionary events for each of the optimal scenarios (−Df option). They are visualized on the species tree in Figure 3. First, we have the duplication of Arabidopsis thaliana (ARATH), which is fully supported by the embedding and bootstrap analysis (blue star 1). The second duplication in Magnoliophyta is supported by the bootstrap analysis (blue star 2). The next duplication (black star 3) in Clupeocephala is clearly related to the presence of paralogous genes from Tetraodon nigroviridis (TETNG) and Takifugu rubripes (FUGRU). Possible incongruence in the gene tree in Eutheria clade can be explained by one gene duplication (black star 4). The last duplication (black star 5) is not well supported by the bootstrap analysis. We can also observe an increased frequency of one duplication in Tetrapoda. Both can be explained by the sequence of poorly supported edges from the gene tree (top left part of Fig. 3) with support values 39, 43, 28, and 46. In general, we observe that four gene duplications marked by stars 1–4 are in agreement with the duplications from the embedding. However, the bootstrap analysis suggests higher (older) location of two gene duplications (e.g., one in Bilateria and less likely in Tetrapoda) than proposed by the single DrML analysis.

Similar analysis, by the prototype version of DrML, was performed for the class II peroxidases from wood decaying fungi (Floudas et al., 2012).

4. Conclusion

With DrML it is now possible to efficiently solve the ML reconciliation problem. DrML can facilitate refined estimates of gene duplication scenarios that take the branch lengths of the species tree into account using our generalized ML model.

Future work will include extensions of DrML that implement solutions to unrooted versions of the ML reconciliation problem and supertree inference based on this problem.

Acknowledgments

This work was conducted in part with support from Gene Tree Reconciliation Working Group at NIMBioS through NSF award EF-0832858. Paweł Górecki and Oliver Eulenstein were supported by a grant from NCN (2011/01/B/ST6/02777). Oliver Eulenstein was supported in part by NSF awards 0830012 and 10117189.

Disclosure Statement

The authors declare that no competing financial interests exist.