FIG. 1.
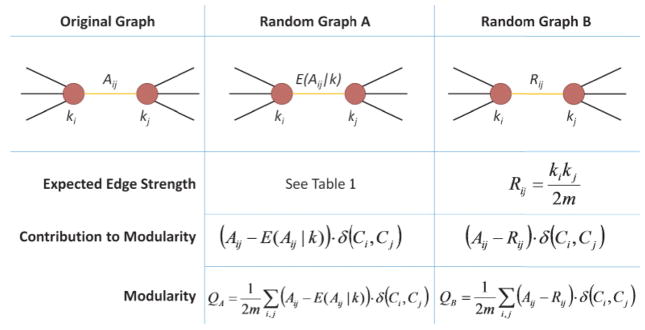
Random graph models and modularity. First column: Nodes i and j of the original graph are connected with an edge Aij. Second column: Random graph A has the same node degrees ki and kj as the original graph, but the edge strength is replaced by its conditional expected value E(Aij|k), with analytic expressions given in Table I. The contribution of this edge to modularity is Aij − E(Aij |k) when the two nodes are assigned to the same group, and the total modularity involves a sum over all edges of the graph. Third column: Similarly for random graph B, with the exception that Rij in Eq. (1) is used instead of the conditional expected edge strength.
