Figure 3.

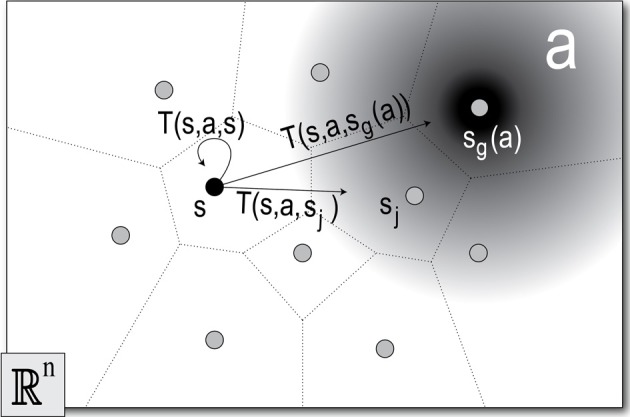
The discrete state-action space. The sample set Q = {q_j|j = 1 … m} (dots) defines the Voronoi regions, or states S = {s_j|j = 1 … m} (bounded by dotted lines). An action a (gradient), exploits MoBeE's attractor dynamics to pull the robot toward some goal state, s_g(a) ∈ S. When the robot is in the initial state, q(t₀) ∈ s, and the agent selects a, MoBeE switches on the attractor (Equation 1) at the point q_g ∈ s_g(a). The agent then waits for the dynamical system to settle or for a timeout to occur, and at some time, t₁, checks which of the states, s_j contains the final real valued configuration of the robot, q(t₁). Often the state-action, (s, a), terminates in the goal state s_g(a), but sometimes, due to constraint forces, it does not. This gives rise to a set of state transition probabilities T(s, a) = {T(s, a, s′₁), T(s, a, s′₂), …, T(s, a, s′_m)}, which correspond to the states, {s_j|j = 1 … m}.