Two Barriers or not? Dynamic Force Spectroscopy on the Integrin α₇β₁ Invasin Complex

Abstract

Dynamic force spectroscopy was used to test force-induced dissociation of the complex between the integrin α₇β₁ and the bacterial protein invasin. Both proteins were used in truncated forms comprising the respective binding sites. Using the biomembrane force-probe, the bond system was exposed to 14 different loading rates ranging from 18 pN/s to 5.3 nN/s. At each rate, bond rupture spectra were collected. Median forces ranged from 8 to 72 pN. These showed two linear regimes when plotted against the logarithm of the force-loading rate. However, a statistical analysis of the full rupture force spectra including the detection limits of the setup showed that all measured data are well described by dissociation over a single barrier.

Introduction

Integrins are heterodimeric transmembrane proteins that mediate adhesion to the extracellular matrix (ECM) and cell-cell-interactions. Their extracellular domains bind directly to molecules of the ECM, whereas their intracellular domains associate with several adaptor and signaling molecules and also connect to the force-generating actin-myosin cytoskeleton (1–3). Integrins not only convey mechanical forces but also relay signals of the ECM into the cell and vice versa, called outside-in and inside-out signaling, respectively (1). These regulatory processes are brought about by several, still only partially understood, conformational changes of the integrin molecules (2).

The unique mechanical function of integrins is exploited by bacteria of the Yersinia family, which presents invasin as a surface molecule that had been shaped by convergent evolution to mimic the physiological integrin binding partner fibronectin (3). Invasin is recognized by the integrins α₇β₁, α₃β₁, and α₆β₁, which finally results in the active uptake of the pathogenic bacterium by the host cell (4). The pathological complex of invasin and integrin is characterized by a very high affinity as compared to other integrin-ligand interactions (4). This exceptional stability of the bond serves to maximize bacteria uptake. Moreover, it offers unique possibilities to explore the intrinsic features of the bond by dynamic force spectroscopy.

The basic experiment in dynamic force spectroscopy is to expose a single bond to a slowly increasing force in the picoNewton range and measure the force at bond rupture, which is called “yield force” in the following. Because the bond system is subject to thermal fluctuations, bond breakage is a stochastic process resulting in a spread of yield forces. Thus, the basic experiment must be repeated many times to collect spectra of yield forces (5). Experimental realization of dynamic force spectroscopy requires a very soft force sensor and immobilization of the binding partners to at least micron-sized objects for manipulation.

For our experiments we used the biomembrane force-probe (BFP) (6,7), which employs an osmotically swollen red blood cell as the ultrasoft spring. As is very common in dynamic force spectroscopy, rupture forces of single bonds ranged from <1 picoNewton to >100 picoNewtons in one spectrum. In this situation, it is unavoidable that the lowest rupture forces are obscured by thermal fluctuations of the ultra-soft force transducer and the environment. This sets a natural low-force detection limit of the method. Obviously, such a limitation might affect the final interpretation of the experiment. In our force spectroscopy experiments of α₇β₁-invasin integrins, we carefully determined force detection limits for each experimental condition applied and discuss their possible impact on the features of the bond energy landscape derived from data analysis.

Materials and Methods

Biomembrane force-probe technique

The biomembrane force-probe (BFP) (6) consists of an osmotically swollen human erythrocyte aspirated by a micropipette, the so-called probe pipette. In this setup, the complementary binding partners were covalently anchored to two sets of microbeads. A bead carrying invasin was glued to the apex of the biotinylated erythrocyte by biotin-neutravidin bonds, whereas a bead carrying integrin was held directly by an opposing pipette, the test pipette.

The suction pressure of the probe pipette induces mechanical tension in the erythrocyte membrane, which enforces a shape of constant mean curvature on the free part of the membrane. The deformation of the erythrocyte upon application of an external force is governed by membrane tension, shown to dominate over other deformation modes (6,8). This gives rise to a linear force-elongation relation for bead displacements below ∼300 nm (7) and ensures that at fixed retraction speed, the bond formed between a pair of complementary beads is loaded at a constant force rate, r. The rupture force can be calculated from the elongation of the erythrocyte at bond rupture, if axial symmetry is maintained throughout the pull. In our setup, the elongation was monitored by video microscopy and real-time tracking of the probe bead position. The spring constant of the BFP was varied from 37 pN/μm to 580 pN/μm by changing pipette pressure and diameter.

Protein immobilization on beads

We based the immobilization protocol on previous works (9,10) and adapted it for our studies on integrin α₇β₁-invasin, as detailed in Ligezowska et al. (11). In this procedure, molecules are linked to the bead surface via a swollen and charged layer of dextran. All linkages are covalent, ensuring that, once formed correctly, bonds also break at the correct location. Moreover, the dextran hydrogel prevents protein denaturation. The electrostatic repulsion between probe and test bead is tuned to minimize nonspecific attachments, and charged carboxyl groups in the hydrogel serve as reactive groups for protein binding.

Ligands and receptors were immobilized onto melamine beads with diameters of 2.55 and 3.27 μm. Melamine particles give highly contrasted microscopic images due to a high index of refraction. Moreover, they carry free amino groups that are well suited for covalent coupling of molecules to the bead surface. The larger bead, referred to as the test bead, carried the integrins. The smaller bead, called the probe bead, carried the invasin alongside with neutravidin that allowed attachment to biotinylated erythrocytes. Protein coupling was performed exactly as described in Ligezowska et al. (11) via covalent attachment of dextran followed by carboxylation of the polymer and subsequent coupling of proteins by active ester chemistry.

We used a recombinant α₇β₁ integrin molecule, which comprised the entire extracellular domains of both integrin subunits and harbored the ligand-binding site. This integrin construct, termed soluble α₇β₁ integrin (12), abrogates the usage of detergents that might damage erythrocyte membranes. The domain of invasin containing the integrin-binding site was produced as in Eble et al. (4). Neutravidin was commercially obtained (Pierce, Stowe, VT and Invitrogen, Carlsbad, CA) and used as in Ligezowska et al. (11). Biotinylation of erythrocytes was performed with Biotin-PEG-NHS 3400 (Nektar Therapeutics, San Francisco, CA) as in Ligezowska et al. (11).

In a previous study, we showed that the binding activity of integrin α₇β₁ is strongly influenced by the divalent cations Mn²⁺ and Mg²⁺ (11). These ions act synergistically, and not only increase the strength of individual bonds but also affect the likelihood of multiple-bond formation. For this study, we used 5 mM Mn²⁺ and 2 mM Mg²⁺, which warranted full integrin activity (11). The measurement buffer contained 30 mM Tris (Sigma-Aldrich, St. Louis, MO), 5 mM MnCl₂ (Merck, Rahway, NJ), and 2 mM MgCl₂ (Sigma-Aldrich) in water, at pH 7.3. A round shape of erythrocytes, required for the proper force determination (7), was enforced by setting the osmolarity of the measurements buffer to 155 mOsm/L by addition of NaCl (Merck).

Single-bond regime

To ensure predominantly single-bond rupture, we used the strategy of competitive blocking. That is, we reduced the number of integrins available for bond formation by titrating with the soluble invasin as blocking agent (11). A concentration of 9 nM invasin optimally reduced the formation of multiple bonds without compromising high binding frequencies. Increasing invasin concentration to 12 nM only had a minor effect on the rupture force distribution while significantly reducing the specific binding frequency of α₇β₁-integrin (11). The frequency of nonspecific bindings was found to be 8%.

Occasionally, highly active and strongly binding beads were observed within each bead preparation lot. Such beads, which probably presented a protein aggregate at an unfavorable location, were immediately discarded. As further precaution, beads were changed frequently within each measurement series to minimize the effect of interbead variation. On average, 12 different bead combinations were used for one complete measurement series.

Experimental setup

The instrument was described in detail in Strigl et al. (9) with modifications as described in Loritz et al. (13). In essence, the experiments were conducted on the stage of a bright-field microscope equipped with a CMOS camera for fast image recording (∼400 Hz frame rate). Micromanipulation was performed with two glass micropipettes, prepared and calibrated according to procedures developed by Evans (8) and as described in detail in Ligezowska et al. (11). Pipette inner diameters ranged from 1.7 to 2.0 μm. Suction pressures calculated to achieve the desired stiffness of the force probe (7) were applied with an accuracy of 0.5 Pa (14). Glass surfaces were blocked with 1% (w/v) BSA (Sigma-Aldrich) in measurement buffer. Pipettes were also filled with this supplemented buffer, whereas the chamber was filled with unsupplemented buffer. The chamber was open on two opposing sides for easy pipette access. The test bead was moved back and forth by a piezo actuator. Probe bead positions were determined to an accuracy of 5 nm by a nonlinear least-squares Gaussian fit.

Data analysis

The yield force (force at bond rupture) was calculated from the maximum displacement of the probe bead during bond loading. The displacement was determined as the difference between probe bead positions at rest and at bond rupture (compare to Fig. 1). To avoid biasing caused by discrete sampling, maximum positions were extrapolated with half the piezo displacement between subsequent tracking points (9). Ruptures with tracking errors near the maximum were excluded. To minimize the influence of force probe relaxation (13) and to average out Brownian fluctuations, the rest position was calculated as the median of positions obtained in a 0.6 s time interval, the “rest” interval, starting 0.3 s after bond rupture. Rupture events were only accepted (99.7% confidence level) if the maximum displacement exceeded three times the SD, σ_x, of bead positions recorded during the rest interval.

Figure 1.

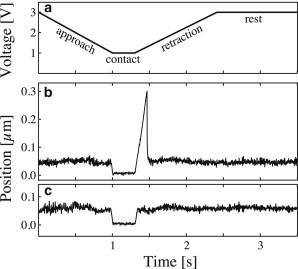
Typical probe bead tracking curves. (a) Piezo control motion cycle. (b) Probe bead tracking in case of a binding-rupture event. As piezo voltage decreases, the test bead is brought into contact with the probe bead, and the motion is stopped for 0.3 s to allow for bond formation. During contact, the erythrocyte is slightly compressed, and the probe bead is pushed away from its rest position (impingement force 6 pN). During retraction, the probe bead is pulled by the test bead until the point of bond rupture (force loading rate 286 pN/s, rupture force 39 pN). Finally, the probe bead returns to its rest position. (c) Probe bead tracking in the case of no bond formation, impingement force 8 pN. Probe stiffness was 150 pN/μm in panels b and c.

Binding frequency was defined as the ratio of the number of rupture events to contact events. An event was accepted as contact if the median probe bead position just before piezo retraction was below its rest position by at least 1σ_x. Impingement forces were calculated from the backward probe displacement recorded during bead contact. Although great care was taken to keep these displacements uniform by continuously monitoring and repositioning pipettes, measured impingement forces deviated up to 70% from the mean value within a measurement series. Between different measurement series, the variation was even greater, due to the wide range of spring constants (see Table 1 as well as Table S1 in the Supporting Material).

Table 1.

Key parameters of measurements

Series ID	No. of valid ruptures	Bond frequency [%]	k [nN/μm]	r [nN/s]	fl [pN]	f† [pN]
1	20	30	0.077	0.018	2.3	10
2a	25	14	0.037	0.024	1.3	8
2b	139	36	0.076	0.025	2.1	12
2∗	164	—	—	0.025	—	11
3	441	28	0.077	0.049	2.2	15
4a	259	42	0.16	0.11	3.4	18
4b	219	31	0.077	0.12	2.2	15
4∗	478	—	—	0.12	—	16
5a	174	42	0.15	0.20	3.6	24
5b	88	52	0.077	0.21	2.5	23
5∗	262	—	—	0.20	—	23
6a	275	40	0.14	0.27	2.8	26
6b	276	39	0.20	0.29	3.7	29
6∗	551	—	—	0.28	—	28
7	381	51	0.19	0.40	4.3	38
8a	49	39	0.35	0.53	7.3	34
8b	254	33	0.16	0.57	3.9	43
8∗	303	—	—	0.56	—	41
9a	426	36	0.35	0.81	6.7	43
9b	215	46	0.19	0.82	4.0	46
9∗	641	—	—	0.82	—	44
10	126	49	0.18	1.3	3.1	56
11	641	47	0.35	1.6	6.6	53
12	417	47	0.35	2.2	6.0	62
13	639	61	0.48	3.3	8.9	65
14	210	55	0.58	5.3	10.1	72

Series have been sorted according to increasing loading rate. Series that are labeled with identical numbers but different characters have almost the same force-loading rates, but possess different spring constants. Whereas these series were treated separately during analysis, they have been merged in Figs. 4 and 5 for clarity. Merged series are denoted with an asterisk. With the exception of binding frequency, all parameters were calculated after a preprocessing routine that filters out events with abnormal pulling velocities. Abbreviations: k, spring constant; r, loading rate; f_l, detection limit; and f^†, median yield force. For statistical uncertainties, see Table S1 in the Supporting Material.

To correctly identify and categorize measured yield forces, individual force loading rates, r, were estimated for each binding. Due to the extension-dependent elasticity of bonds and linkers (15), r is a monotonically rising function of the stretch length. In this study, r was approximated by $k\times {\overline{\nu }}_{\text{bfp}}$ where k is the calculated spring constant of the probe, and ${\overline{v}}_{\text{bfp}}$ is the average velocity of the probe bead during bond stretching. The values summarized in Table 1 and Table S1 are ensemble medians.

Estimates of the statistical uncertainties of fit parameters and median yield forces were produced by nonparametric bootstrapping (16). We used the software routine BOOTRSP.M published in Zoubir and Iskander (16) to create synthetic data sets from the original data by random resampling with replacement. The generated data sets were treated and fitted exactly as the measured data.

Theoretical Considerations

Our understanding of force-induced bond dissociation is rooted in the pioneering work of Bell (17) and Evans and Ritchie (5), who explained bond breakage as a thermally driven process within the framework of chemical reaction rate theory. In this framework, the unbinding rate, ν_→, is proportional to the likelihood of reaching a transition state in a quasi-static equilibrium set by a sharp energy barrier, U_b, located at coordinate z_b along the reaction path. As a consequence of the work performed by the force f, this barrier is lowered by f × z_b resulting in

$${\nu }_{\to }\left(f\right)\propto \text{exp}\left(-\frac{U_b-f{z}_b}{k_{\text{B}}T}\right),$$ (1)

from Evans and Ritchie (5). Thus, the unbinding rate is expected to rise exponentially with force (17)

$${\nu }_{\to }\left(f\right)={\nu }_0\text{exp}\left(\frac{f}{f_b}\right),$$ (2)

where ν₀ is the force-free dissociation rate and f_b is the characteristic force given by k_BT/z_b.

In the simplest case, chemical kinetics of first order can be assumed. Moreover, the force is ramped up in a linear fashion, f = r × t. Therefore, in the kinetic equations, time can be effectively replaced by force. Because an external force strongly diminishes the probability of rebinding, the latter can be neglected entirely, resulting in a likelihood of bond survival given by Evans and Ritchie (5):

$$P_r\left(f\right)=\text{exp}\left(-\frac{1}{r}\underset{0}{\overset{f}{\int }}{\nu }_{\to }\left(f^{\text{'}}\right)d{f}^{\text{'}}\right).$$ (3)

For a single barrier, integration yields

$$P_r\left(f;{\nu }_0,\alpha \right)=\text{exp}\left(-\frac{{\nu }_0}{r}\frac{\text{exp}\left(\alpha f\right)-1}{\alpha }\right).$$ (4)

Here, the reciprocal of the characteristic force, α ≡ f_b⁻¹, has been introduced for convenience. From the likelihood of bond survival, the observable distribution of yield forces, p(f), is easily calculated by p(f) = dP/df, while the most probable yield force, f^∗, is calculated as maximum of p(f) resulting in

$$f^{\ast }=f_b\text{ln}\frac{r}{r_0},$$ (5)

from Evans and Ritchie (5), where r₀ ≡ ν₀f_b. Thus bond strength, f^∗, is a dynamic property that depends logarithmically on the loading rate.

The simplification above breaks down at very low force loading rates due to rebinding of already broken bonds (18) and at very high rates due to insufficient relaxation (19). Moreover, it neglects shifts of the barrier position with the acting force that may cause additional deviations (20). Still in most instances, this straightforward description, often called standard theory, adequately describes measured data.

In the traditional approach of dynamic force spectroscopy, measured strengths, f^∗, are plotted against loading rates, r, in a semilogarithmic plot to extract the model parameters f_b and ν₀ by the best line fit. If, however, force spectra are broad and exhibit no clear maxima, or if significant parts of the spectra are below the detection limit, f_l, of the measurement technique, it is advantageous to instead plot median forces, f^†, of the spectra against r and obtain model parameters by a fit to (9)

$$f^{†}=f_b\text{ln}\left[\text{exp}\left(\frac{f_l}{f_b}\right)+\frac{r}{r_0}\text{ln}\left(2\right)\right].$$ (6)

Whenever the potential exhibits several (sharp) barriers, the logarithmic behavior of Eqs. 5 and 6 complexifies into a sum of logarithmic regimes (21–23). In a semilogarithmic plot, this manifests as a set of piecewise linear relations with increasing slopes; compare to Fig. 2. Each increase in slope signifies that an outer barrier has been suppressed by the force f, and that dynamics is now governed by a barrier closer to the potential minimum. In this way, the standard theory can be used to estimate both position and relative strength of principal energy barriers.

Figure 2.

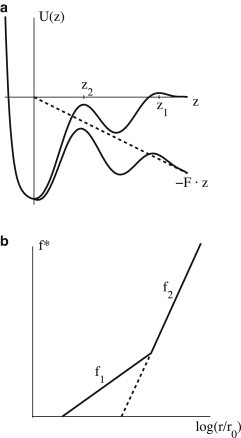
Effect of multiple barriers. (a) A binding potential exhibiting two barriers. Without force (upper curve), unbinding is controlled by the outer barrier at z₁. Application of a force along the z axis (dashed line) lowers the energy progressively and consequently changes the relative strength of the barriers. Beyond a certain force, dynamics is governed by the peak at z₂ (lower curve). (b) In a semilogarithmic plot of bond strength, f^∗, versus loading rate, r, the suppression of the outer barrier results in an abrupt increase of slope. f₁ = k_BT/z₁ is the slope caused by the outer barrier, while f₂ = k_BT/z₂ corresponds to the inner barrier.

For a single-barrier binding energy potential, standard theory predicts a sharply peaking probability density that rapidly falls at forces larger than f^∗. As pointed out by Raible et al. (24), this behavior is observed rarely if ever; instead distributions are consistently found to be much broader with tails extending far into the high force regime—and this indeed is also the case in our measurements.

According to Raible et al. (24), a major shortcoming of conventional theory is that it neglects the statistical spread of the dissociation rate, ν_→, caused by variations in the molecular environment of the bonds, structural and orientational fluctuations, and the stochastic impact of nonspecific interactions (24). To cope with this complexity, the group proposed a probabilistic extension to the formalism in which the single value of the reciprocal characteristic force α is replaced by a distribution, ρ(α). This accounts for the fact that dynamic force spectroscopy probes ensembles of bonds; each bond experiences its own unique environment. The most obvious choice for ρ(α) is a Gaussian (width σ, center α_m) truncated by a Heaviside step function at zero:

$$\rho \left(\alpha ;{\alpha }_m\mathrm{,}\sigma \right)=N\text{exp}\left(-\frac{{\left(\alpha -{\alpha }_m\right)}^2}{2{\sigma }^2}\right)\Theta \left(\alpha \right).$$ (7)

Indeed, this choice convincingly reproduces experimental data (24). By introducing a spread in α, the total number of fitting parameters is increased to three. The likelihood of bond survival in this formalism is found from a convolution of ρ(α; α_m, σ) and Eq. 4,

$$P_r\left(f;{\nu }_0,{\alpha }_m,\sigma \right)=N\underset{0}{\overset{\infty }{\int }}\text{exp}\left(-\frac{{\nu }_0}{r}\frac{\text{exp}\left(\alpha f\right)-1}{\alpha }-\frac{{\left(\alpha -{\alpha }_m\right)}^2}{2{\sigma }^2}\right)d\alpha ,$$ (8)

where the normalization constant, N, is inherited from Eq. 7.

With the convolution approach of Eq. 8, the logarithmic relationship between bond strength, f^∗, and loading rate, r, is lost, and the justification of parameter determination via linear interpolation of a (ln(r), f^∗) plot breaks down. Although numerically this approach still works surprisingly well (24), direct fits to measured force spectra also exploit the fact that the model parameters ν₀, α_m, and σ not only affect f^∗ but also the specific shape of the force spectra. The latter method is thus more stringent. Additionally it sidesteps elegantly the problem of localizing maxima in broad and noisy spectra.

In the following, we first use the conventional approach based on the standard theory (5,6) to extract the parameters f_b and ν₀. Because measured spectra are broad, with smeared-out peaks and long tails toward high forces, we plot median forces, f^†, versus r, instead of most probable force, f^∗, versus r, as in the standard method. We define and include detection limits, f_l, of each force spectrum, which are often neglected in the conventional approach. Because measured spectra exhibit long tails toward high forces, which cannot be accounted for in the standard methods, we apply in a second step the probabilistic extension to the standard theory, as proposed by Raible et al. (24). We compare intrinsic bond parameters obtained from the conventional and from the extended approach. Moreover, we explicitly included force detection limits and discuss possible consequences for data interpretation.

Results

Imperative to any study of single-bond force spectroscopy is to reduce as much as possible the impact of rupture events that do not originate from the correct bond-pair or that were not measured under controlled conditions. In this study, we adopted several measures to minimize the impact of such ill-defined events. One important step was to optimize the immobilization protocol and experimental procedures as described in Materials and Methods. As an additional step, we devised a data filtering approach that removed some of the remaining ill-defined events.

Data filtering

At the level of individual measurements, the BFP technique offers no direct way to distinguish between single and multiple bond ruptures or nonspecific events, but the instantaneous probe bead velocity, v_bfp, during bond stretching provides indications of the nature of the bond. Due to the combined elasticity of bonds and linkers, designated below by k_link, the probe bead velocity, v_bfp, lags that of the piezo, v_piezo, by

$$v_{\text{bfp}}=v_{\text{piezo}}\frac{k_{\text{link}}}{k+k_{\text{link}}},$$ (9)

where k is the spring constant of the erythrocyte membrane. Usually the difference amounts to a few percent (see Table S1). An abnormally high ratio of v_bfp to v_piezo corresponds to a connection between beads of extreme stiffness likely caused by specific or nonspecific bonds acting in parallel. In fact, based on the substantially higher spatial resolution of AFM, a similar argument has been previously used to determine the number of bonds contributing to single dissociation events (25). Extremely stiff contacts might involve regions where the dextran layer is shallow and, accordingly, nonspecific interactions between beads are highest.

Aberrantly low ratios of v_bfp to v_piezo were observed in approximately one of four events. In most of these cases, the position of the probe bead suddenly stopped for a retraction length of up to ∼120 nm, after which it resumed its normal motion according to Eq. 9. A similar phenomenon has been reported for AFM experiments, as published by, e.g., Florin et al. (26) and Lo et al. (27), where it has been assigned to the serial rupture of multiple bonds. For our system, a stop-go behavior might be attributed to occasional unraveling or entanglement of loaded dextran filaments held together by nonspecific interactions, or alternatively, breakage of weak bonds caused by denatured protein.

Abnormal probe bead velocities indicate nonidealities like the stop-go behavior mentioned above and cause an additional spread in the force spectrum. Therefore, rupture spectra were filtered according to the mean velocity of the probe bead during bond stretching, discarding rupture events belonging to the upper 5% and the lower 30% of recorded bead velocities. This procedure is in many ways analogous to the jump-length selection criterion used in AFM-based experiments (28,29).

Fig. 3 shows the effect of velocity filtering on a representative measurement series. Our filter procedure primarily removes events at the low force end of the distribution, pointing at nonspecific events as sources of abnormal rigidities of interbead connections.

Figure 3.

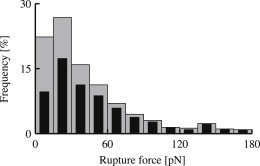
Effect of filtering. (Histogram) Detected bond ruptures during measurement series 7 (Table 1), depicting rupture force distribution before (shaded bars) and after (solid bars) data filtering with respect to recorded probe bead velocity during bond stretching.

Detection limit of force measurement

The detection limits, f_l, listed in Table 1 correspond to different choices of probe spring constants, k. The rupture identification procedure (see data analysis) effectively sets a lower detection limit of

$$f_l=k\times 3{\sigma }_x,$$ (10)

where k is the spring constant of the probe, and σ_x is the SD of the bead rest position after bond rupture (see Materials and Methods). The values listed in Table 1 were calculated from Eq. 10 using ensemble medians, encompassing all recorded fluctuations of the probe during its resting intervals. These fluctuations arise from two sources: measurement uncertainty and thermal noise. The latter can be estimated from the equipartition theorem. Assuming uncorrelated noise sources, an approximate expression for f_l can be given in terms of temperature, T, and spring constant, k:

$$f_l=3{\left(k{k}_{\text{B}}T+k^2{\sigma }_{det}^2\right)}^{1/2}.$$ (11)

Here, σ_det denotes the SD due to measurement uncertainty which, for the current system, was estimated to ∼5 nm by a similar approach as in Simson et al. (7). With this value, Eq. 11 closely reproduces the experimentally determined values of f_l given in Table 1.

Twenty distinct rupture spectra of the bond system integrin α₇β₁-invasin

In dynamic force spectroscopy, measurements at different force-loading rates are compared to gain insight into the energy landscapes of the bonds. Here, the rupture force spectrum for α₇β₁ integrin-invasin was measured at 20 distinct combinations of pulling speed, ${\overline{v}}_{\text{bfp}}$, and spring constant, k. In a previous BFP study conducted on protein A-IgG bonds, Nguyen-Duong et al. (30) reported yield forces to systematically increase with transducer stiffness, even when correcting for the expected shift in the probe detection limit. Thus, in six cases we realized approximately the same loading rate by two different combinations of speed and stiffness resulting in 14 distinct force loading rates that cover an interval from 18 pN/s to 5.3 nN/s. In our case, however, no significant differences between these series of loading rates could be observed. For this reason, Figs. 4 and 5 present only merged series. The key parameters of each spectrum are listed in Table 1. Fig. 4 depicts the spectra as force histograms with a universal bin size of 15 pN, whereas Fig. 5 shows accumulated distributions, in which force events have been summed up according to

$${\Phi }_r\left(f\right)=\frac{1}{N_r}\sum _{n=1}^{N_r}\Theta \left(f-f_n\right).$$ (12)

Here f_n represents the N_r discrete yield forces measured at loading rate r.

Figure 4.

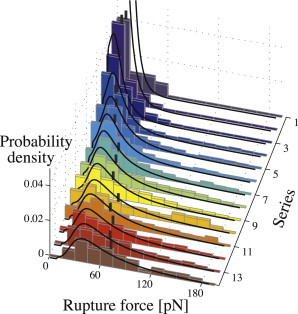
(Histogram) Measured yield force spectra. The numbering scheme of the z axis has been adapted from Table 1. Loading rate increases toward the front. (Vertical bars) Individual median yield forces. (Curves) Best fit of the Raible model (24) obtained through minimization of Eq. 16 resulting in the model parameters ν₀ = 1.4 s⁻¹, α_m = 10⁻¹⁰ pN⁻¹, and σ = 0.103 pN⁻¹.

Figure 5.

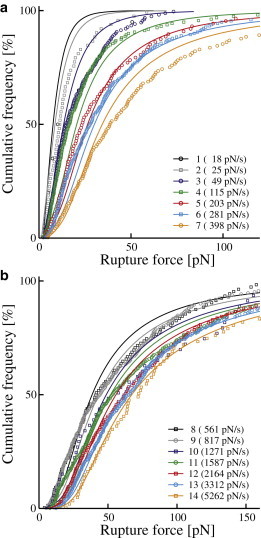
Cumulative rupture force distributions. (a) Measurement series 1–7 and (b) measurement series 8–14. Only every third measurement point is depicted to reduce complexity. The legends show identification number (Table 1) as well as median force loading rate for each measurement series. (Circles and squares) Measured data; (solid curves) best fit of the Raible model as shown in Fig. 4.

As predicted by theory, both shape and position of the force distributions are affected by the loading rate. An increase in loading rate broadens the spectrum while shifting the entire distribution toward higher values. The resulting increase in median yield forces—from 10 pN to 72 pN—is illustrated in Fig. 4.

Fig. 6 depicts the explicit relation between median yield force, f^†, and loading rate, r. Horizontal error bars mark the 16th and 84th percentile of the loading rate distribution, which was calculated as the product of the probe spring constant, k, and individually recorded probe bead velocities, ${\overline{v}}_{\text{bfp}}$. The corresponding uncertainties on the median yield forces were estimated by 2500 iterations of bootstrapping on the respective data set (compare to Materials and Methods). The vertical bars shown mark the 16th and 84th percentile of the calculated parametric distribution of f^† (see also Table S1).

Figure 6.

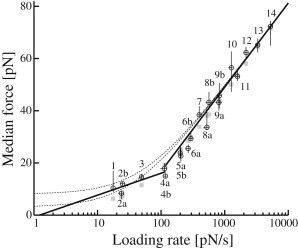
Semilogarithmic plot of median yield forces, f^†, versus loading rate, r. (Circles) Measured data points (see main text for error bars). (Solid lines) Best line fits—weighted according to error bars—of points 1–4 and points 8–14, respectively. Points 5–7 were left out to avoid a possible crossover regime. From the steep line at high force loading rates, standard theory model parameters f_b = 14 pN and ν₀ = 1.5 s⁻¹ were estimated using the approach of Evans and Ritchie (5). (Dashed curves) Extrapolations of this fit into the low loading rate regime using Eq. 6 and, for demonstration, two realistic force detection thresholds, fl = 3 pN (lower curve) and fl = 8 pN (upper curve). (Shaded squares) Fitted values produced by nonlinear cost function minimization including individual force-detection limits (see Eq. 14). Fit results f_b = 15 pN and ν₀ = 2.3 s⁻¹.

The conventional approach of Evans and Ritchie

In the conventional approach of Evans and Ritchie (5), the model parameters, f_b and ν₀, are determined from a semilogarithmic plot of measured bond strength, f^∗, versus applied loading rate, r. This straightforward approach requires a precise determination of the distribution peaks. In our case, distributions are relatively broad with smeared-out peaks. Moreover, some spectra extend substantially below the detection threshold, f_l, with an inherent risk that the true peak of the distribution remains hidden. Therefore, we applied the alternative approach of plotting force medians, f^†, instead of bond strengths, f^∗, versus r; see Theoretical Considerations and Fig. 6.

The standard theory predicts a logarithmic dependence of bond strength on loading rate (see Eq. 5). From Eq. 6, the same kind of relation can be expected between f^† and r whenever

$$\frac{r\text{ln}2}{{\nu }_0{f}_b}>>\text{exp}\left(f_l/f_b\right).$$ (13)

The corresponding semilogarithmic plot of our data, Fig. 6, exhibits two linear regimes: a low slope regime at force loading rates below 100 pN/s and a regime with a steeper slope at higher rates. This seemingly indicates a multiple-barrier bond system, in which a dominant outermost energy barrier is suppressed as force ramps-up, whereby dynamics is controlled by a barrier closer to z = 0 (21,23).

For the very highest loading rates, the criterion Eq. 13 is fulfilled, and the parameters of the standard model can be estimated from the line fit provided in Fig. 6 for which error bars of both force loading rate and force median have been taken into account. This gives f_b = 14.1 pN and ν₀ = 1.5 s⁻¹. Uncertainties were analyzed by bootstrapping (see Materials and Methods, 5000 iterations) revealing symmetrical fluctuations of the fit results with SD of 1.3 pN and 0.4 s⁻¹, respectively. The normalized χ² value of the fit was 0.2.

To check the validity of Eq. 13 in the low force regime, we used the model parameters f_b and ν₀ found for the high force regime along with the detection limits, f_l, estimated for the low force regime (see Table 1). We conclude that although force spectra in this regime were measured with soft springs and consequently low detection limits, the loading rates are still too low to ensure a purely logarithmic relation. As a consequence, linear behavior of median yield forces cannot be expected below ∼400 pN/s. This is illustrated in Fig. 6 where median yield forces as expected from Eq. 6 have been plotted over the full range of loading rates (dashed curves). The values of f_b and ν₀ determined for the high loading rate regime and two realistic values of the detection limit, 3 and 8 pN, respectively, were used for this extrapolation. A detection limit of 3 pN is representative at the lowest loading rates (see Table 1) and, strikingly, the corresponding curve approximates the measured points surprisingly well in exactly that part of the plot.

This demonstrates that the unavoidable low force cutoff of the method may give rise to an entirely artificial two-regime behavior. When bond rupture forces are of the same order as force detection limits, which is the case in the low force regime of our data (Table 1 and see Table S1), a strong artificial shift of the force median is inevitable because a large part of the spectrum remains hidden. By linear fitting, this artificial shift might be mistaken for a second, outlying energetic barrier.

The value of f_l = 8 pN used as basis for the second curve of Fig. 6 roughly corresponds to the detection limit of the probe at very high loading rates. In this part of the regime, f_l is seen to be of minor importance because both curves approach the experimental data asymptotically. This is to be expected for high force loading rates, where the major part of the force spectrum falls far away from the detection limit, and only a small fraction of ruptures remains hidden. Please note that the dashed curves were included merely to illustrate the influence of (realistic) fixed force thresholds on median forces and do not present actual fits. The necessary data fitting is complicated by the fact that detection limits vary discretely from spectrum to spectrum (Table 1), thus a discrete fitting approach is necessary.

The entire data set of median forces versus loading rates can be included if a nonlinear fit is conducted on the full expression, Eq. 6. This approach, however, must be designed carefully because f_l changes from one measurement to another due to the variety of spring constants applied (see Table 1). In the procedure chosen here, the nonlinear fit is obtained by minimization of the cost function,

$$Q\left({\nu }_0,f_b\right)=\sum _r{\left(f_r^{†}\left({\nu }_0,f_b\right)-{\tilde{f}}_r^{†}\right)}^2,$$ (14)

where f_r^†(ν₀,f_b) represents the theoretical expression of Eq. 6, and ${\tilde{f}}_r^{†}$ is the measured median at loading rate r. For the calculation of the former, spectrum specific values of f_l have been taken from Table 1. Minimization leads to f_b = 15.3 pN and ν₀ = 2.3 s⁻¹. Again, uncertainties were analyzed by bootstrapping (see Materials and Methods, 5000 iterations). We found symmetrical fluctuations of the fit results with SDs of 0.9 pN and 0.2 s⁻¹, respectively. The normalized χ² value was 4.3. One cause for this somewhat high value is that SD of f_l and force-loading rate could not be included.

The approach of Raible et al.

We used the approach of Raible et al. (24) in addition to the conventional approach because measured spectra displayed pronounced tails toward high forces whereas standard theory predicts a rather sharp decay of spectra beyond the maximum. In the approach of Raible et al. (24), parameter determination relies on a full-scale fitting method whereby each measured yield force is taken into account. To correctly compare measurements with theory, theoretical distributions obtained through Eq. 8 must be restricted to the detection limits of the measurement technique by imposing a lower threshold, f_l:

$$P_r^{\text{'}}\left(f;{\nu }_0\mathrm{,}{\alpha }_m\mathrm{,}\sigma \right)=(\begin{array}{cc}1& \text{for}f\le f_l\mathrm{,}\\ \frac{P_r\left(f;{\nu }_0\mathrm{,}{\alpha }_m\mathrm{,}\sigma \right)}{P_r\left(f_l;{\nu }_0\mathrm{,}{\alpha }_m\mathrm{,}\sigma \right)}& \text{for}f>f_l.\end{array}$$ (15)

The comparison is conducted through an adequate cost function, Q(ν₀, α_m, σ), which upon minimization leads to optimum fit parameters. Here, we adopted the norm-2 approach of Raible et al. (24) that treats every measurement point on an equal footing:

$$Q\left({\nu }_0,{\alpha }_m,\sigma \right)=\sum _{n,r}{\left\{P_r^{\text{'}}\left(f_n;{\nu }_0,{\alpha }_m,\sigma \right)-\left[1-{\Phi }_r\left(f_n\right)\right]\right\}}^2.$$ (16)

The sum runs over the complete set of yield forces f_n from each series, labeled by r. Φ_r(f) is the measured distribution at r defined by Eq. 12. The force thresholds, f_l, can be set independently for each distribution, P′_r(f). In the implementation presented here, f_l were taken from Table 1.

The best fit obtained through minimization of Eq. 16 is presented as solid curves in Figs. 4 and 5. Although, to reduce complexity, only merged series are depicted, all 20 spectra have been considered individually during fitting. The optimum parameter set was found to be ν₀ = 1.4 s⁻¹, α_m = 1.0 × 1.0⁻¹⁰ pN⁻¹, and σ = 0.103 pN⁻¹. However, the value of 10⁻¹⁰ pN⁻¹ is merely a necessary boundary of the fitting procedure, and the true optimum for α_m is likely to be even closer to zero. Uncertainties of the remaining fit parameters were analyzed by bootstrapping (see Materials and Methods, 110 iterations). Fluctuations in both parameters were symmetrical with SD of 0.004 pN⁻¹ for σ and 0.11 s⁻¹ for ν₀. Root mean-square deviation between fitted and measured cumulative distributions (i.e., (Q(ν₀,α_m,σ)/N)^1/2 with N the number of measured yield forces; see Eq. 16) was 0.06.

A calculation of the average α,

$$\overline{\alpha }\equiv {\int }_0^{\infty }{\alpha }^{\text{'}}\rho \left({\alpha }^{\text{'}};{\alpha }_m\mathrm{,}\sigma \right)d{\alpha }^{\text{'}},$$ (17)

allows the parametric set of the Raible model to be compared with the parameters found with the standard model. Inserting the above results into Eq. 17 gives $\overline{\alpha }\approx 0.0824$ pN⁻¹ corresponding to ${\overline{f}}_b\approx$ 12.1 pN. Setting α_m to zero yields indistinguishable values. Gaussian error propagation results in uncertainties of $\overline{\alpha }$ and ${\overline{f}}_b$ amounting to 0.003 pN⁻¹ and 0.5 pN, respectively.

Discussion

In any study of single-bond force spectroscopy it is of paramount importance to minimize the impact of rupture events that are not measured under well-controlled conditions or do not originate from the specific bond pair to be studied. Besides standard measures to reduce the influence of ill-controlled events (see Materials and Methods), we could further improve data by discarding measurements with abnormal average retraction speed of the probe bead. As detailed under Results, this filtering procedure mostly removes nonspecific events at low forces (see Fig. 3). Whereas this clearly facilitates data analysis and interpretation, it has little effect on the bond parameters retrieved.

Although the Raible approach with its concept of distributed bond properties generally fits the measured force spectra quite well—and indeed much better than the standard theory—some measurement series significantly deviate from the expected behavior (Fig. 4 and 5). For series 8, 10, and 11, the deviation is strongest toward the high end of the spectrum, indicating an unfavorably high contribution of multiple bonds. For other series, e.g., 3 and 7, the discrepancy is distributed more evenly and corresponds to a homogenous noise contribution of nonspecific nature, as illustrated in Fig. 7. Experimental variations, especially those related to the preparation of beads, protein activity and buffer stability are the most likely candidates for this. For the specific case of measurement series 1, poor statistics also plays a significant role. On an overall scale, however, the Raible approach is robust because all data points are included on an equal footing. As a consequence, the results are hardly influenced by deviating measurement series.

Figure 7.

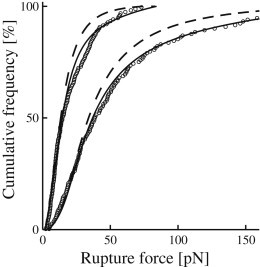
Effect of noise. Cumulative rupture force distributions for measurements series 3 (upper curves) and 7 (lower curves). (Circles) Measured data points (only every third point is depicted). (Dashed curves) Raible fit with fitting parameters as in Figs. 4 and 5. (Solid curves) Raible fit supplemented with a 10% homogeneous noise contribution that covers the full range of measured forces.

At a first glance, the results of the Raible fit of Fig. 4 and 5 are surprising because the (somewhat arbitrary) location of the distribution maximum, α_m = 10 × 10⁻¹⁰ pN⁻¹, corresponds to a dissociation length Δx = α_mk_BT ≈ 4 × 10⁻¹⁹ m, well inside the nucleus of the atom. For other single-bond systems, maximum dissociation lengths in the Ångstrom range have been reported (24). On the other hand, the estimated width of the distribution, σ = 0.103 pN⁻¹ is quite representative for a single-bond system (24). Interestingly, all systems studied by Raible et al. have α-distributions extending into the phenomenological forbidden subatomic scale, and in this light, our system is not substantially different. Our data are in agreement with a notion from Raible et al. (24) that the average, but not the maximum, should be interpreted when using a truncated Gaussian for the distribution of α.

The characteristic force, f_b = 14.1 pN (SD 1.3 pN), and the force-free dissociation rate, ν₀ = 1.5 s⁻¹ (SD 0.4 s⁻¹) ( found in the conventional approach of plotting median-yield forces against loading rate on a logarithmic scale and extracting model parameters by a best-line fit), as well as the values f_b = 15.3 pN (SD 0.9 pN) and ν₀ = 2.3 s⁻¹ (SD 0.2 s⁻¹) (found in the slightly more advanced approach that additionally takes into account a variable detection limit (see Results)), coincide reasonably well with the calculated average value, ${\overline{f}}_b$ ≈ 12.1 pN (SD 0.5 pN) and ν₀ = 1.4 s⁻¹ (SD 0.11 s⁻¹) of the Raible model. Our results thus again confirm an observation made by Raible et al. that the conventional method of Evans and Ritchie (5) leads to good results, even though the theory behind it produces unrealistic narrow distributions of wrong skewness (24).

As highlighted in our analysis, whenever bond strength is of the same order as the detection limit, measured bond strengths deviate from the expected logarithmic dependence on the force-loading rate (Eq. 6) in a manner that can be easily mistaken for a second regime corresponding to an outer barrier with a low characteristic force, f_b. In our case (compare to Fig. 6), the existence of this second linear regime, exhibiting a slope that corresponds to f_b = 3.6 pN and the second barrier at ∼1 nm distance, could not be confirmed by our approach.

Please note that our analysis is based on median values in contrast to the more often used maxima of the yield force distributions. In the latter approach, this maximum is usually found by fitting a Gaussian to the central part of the histogram of yield forces. If the true maximum of the distribution is well above the detection limit of the technique and no part of the fit range is influenced, this approach should be less prone to bias than the median. However, if data are used where thermal and other noise overlap true events, the low-force sides of the measured spectra are distorted. This also produces a bias of the fitted maxima of distributions toward higher values. Thus, no matter which parameter is used in the analysis to describe the dependence of yield forces on force loading rates, one has to take great care to avoid artifacts produced by detection limits of the apparatus. Here, we chose to use the median because the effect of a low-force cutoff on this parameter can be easily incorporated into the respective equations.

Properties of the bond between invasin and α₇β₁ integrin

Invasin forms, with integrins, a complex of very high affinity, exceeding by two orders of magnitude the integrin affinities of native EMC ligands (4) such as fibronectin or laminins. In fact, invasin has been shown to mimic fibronectin, especially by exhibiting two noncontiguous binding sequences, which in three-dimensional protein structures reach out across two neighboring domains (3), but the interdomain sequence linking these two neighboring domains is substantially different in terms of flexibility. In fibronectin, the two binding patches that reside on neighboring domains are flexibly linked, whereas in invasin those two domains are rigidly connected without any structural flexibility. It is hypothesized that this rigidity is the reason for the exceedingly high affinity of invasin for integrins This rigidification could also abolish the ability of the invasin-integrin complex to exist in several distinct states of different bond strengths, exhibited by a fibronectin-integrin α₅β₁ bond (31,32).