Figure 2.

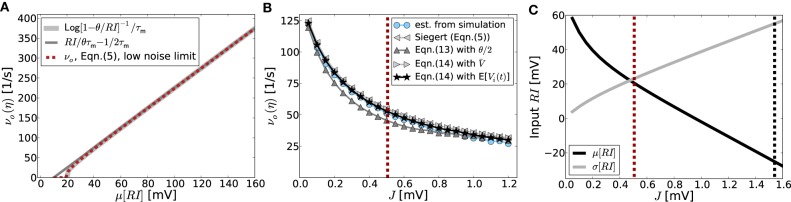
(A) Demonstrates that the input-output-relation of the LIF neuron Equation 5 indeed gets linear in the strongly mean-driven regime. The light gray line shows the f-I-curve in the noise-less case [Equation (10)], dark gray corresponds to its linear approximation Equation (11), while the red curve is the corresponding self-consistent rate given by Equation (5) in the low-noise limit σ[RI] → 0. (B) Shows the output rates as a function of network coupling strength J as they are actually obtained from network simulations averaged over 10 trials (blue dotted curve) vs. the prediction from Equation (5) (gray left-pointing triangles), as well as the linear model prediction Equation (13) with E[V(t)] = θ/2 (dark gray triangles). Also shown is the prediction from solving Equation (14) self-consistently with V = ∫^∞_−∞ VP(V) dV [with stationary membrane potential probability density function P(V) as derived in Brunel (2000); gray right-pointing triangles], as well as from using the estimated average membrane potentials E[V_i(t)] obtained from simulations (black asterisks). The vertical red line represents the expected critical coupling strength J^md_c for the mean-driven regime. The external drive is constant Poissonian noise (η = 3.5), while the local network coupling strength J, and hence μ[RI_s] and σ[RI_s], vary. In this setting the system undergoes a regime change from the mean-driven to the fluctuation-driven scenario. This is demonstrated in (C), where the total mean and standard deviation of RI = R(I_x + I_s) are shown as function of J in black and gray, respectively. The red dashed line corresponds to that in (B), while the black dashed line indicates the critical J^fd_c expected from Equation (9). The corresponding spike activity is shown for three exemplary cases in Figures 1G–I. Other parameters in (B,C) are N = 2500, κ = 250, θ = 20 mV, τ_m = 20 ms, τ_ref = 0.1 ms, and g = 6.