Figure 9.

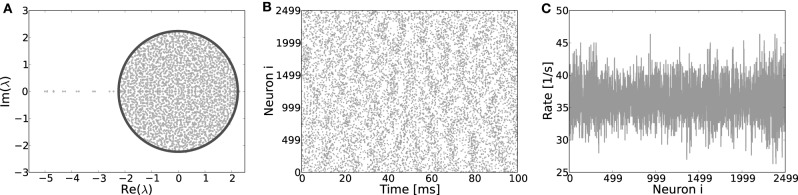
(A) Eigenvalue distribution in the complex plane of a ring network with random assignment of weights, irrespective of the identity of a neuron, hence each existing synapse has weight J with probability β and −gJ with probability (1 − β). These ring coupling matrices have eigenvalue spectra very akin to those of corresponding random networks and most of the eigenvalues adhere to the circle law prediction (Girko, 1984) for random networks $r=\sqrt{Np(\beta +g^2(1-\beta ))-{\mu }^2/N}$ (dark line). Only a few singular eigenvalues on the left of the center indicate the underlying ring topology. The eigenvectors of such “hybrid” ring matrices have no apparent structure and no pattern formation occurs when the system becomes supracritical, as clearly visible from the spiking activity (B) and the rates per neuron (C). Here, J_c ≈ 0.44 mV, simulation parameters J = 0.6, g = 6 and N = 2500.