Figure 2.

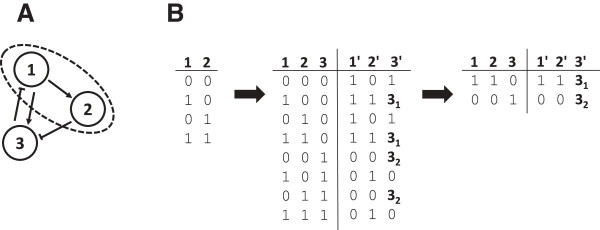
For this simplified account of the algorithm described in the text, we analyze a 3-node network (A). We start with the full listing of all value combinations for nodes 1 and 2 in a 2 x 22 matrix, then add node 3 as described to obtain a (2 + 1) x 22+1 matrix (B). We start with the full listing of all value combinations for nodes 1 and 2 in a 2 x 2² matrix, then add node 3 as described to obtain a (2 + 1) x 2²⁺¹ matrix. For this, we also specify the images 1′, 2′, 3′ to which the three nodes tend for any input combination, using logical parameters. In this simple example, only node 3 receives multiple inputs and thus has non-trivial logical functions. Removing the states which cannot match their image state for any valid choice of the logical functions, we obtain two candidates for fixed states. Comparing the states to their image states, we realize that state (1, 1, 0) is a fixed state if 3₁ equals 0 (i.e., node 3 is not activated by the presence of its activator 1 alone), whereas state (0, 0, 1) is fixed if 3₂ equals 1 (i.e., node 3 is already activated by the absence of its inhibitor 2 alone). Setting both 3₁ = 0 and 3₂ = 1 renders both states fixed. Experimental data in agreement with state (1, 1, 0) but not with (0, 0, 1) thus help in estimating the logical functions.