Differential-Private Data Publishing Through Component Analysis

Abstract

A reasonable compromise of privacy and utility exists at an “appropriate” resolution of the data. We proposed novel mechanisms to achieve privacy preserving data publishing (PPDP) satisfying ε-differential privacy with improved utility through component analysis. The mechanisms studied in this article are Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA). The differential PCA-based PPDP serves as a general-purpose data dissemination tool that guarantees better utility (i.e., smaller error) compared to Laplacian and Exponential mechanisms using the same “privacy budget”. Our second mechanism, the differential LDA-based PPDP, favors data dissemination for classification purposes. Both mechanisms were compared with state-of-the-art methods to show performance differences.

1 Introduction

Dissemination and meaningful use of patient data can help improve treatment satisfaction, quality of life, and various aspects of well-being [1]. However, privacy is a major concern when patient data is used for research purposes [2]. Healthcare data often contain sensitive information about individuals, and publishing such data might violate their privacy. Ensuring privacy while maintaining data utility is one of the most important problems in biomedical research [3, 4]. Loss of privacy is usually associated with failure to control access to information, to control the flow of information, or to control the purposes for which information is employed [5]. To provide strong privacy guarantees and to give researchers greater flexibility in conducting the required data analysis, it is necessary to develop utility-aware privacy preserving data publishing mechanisms. In this paper, we proposed two new privacy-preserving publishing algorithms that can effectively preserve data utility for various data workloads and achieves differential privacy, a rigorous definition that provides a provable privacy guarantee.

1.1 Motivation and Related Work

Data privacy has been an active research topic in statistics, database, and security community for the last three decades [6–9]. Many privacy models, such as k-anonymity [10] and its extensions [11, 12] have been proposed to thwart privacy threats caused by identity and attribute linkages in relational databases. The usual approach is to generalize the records into equivalence groups so that each group contains at least k records with respect to some quasi-identifier (QID) attributes, and the sensitive values in each QID group are diversified enough to prevent confident inferences. A large number of anonymization algorithms [13, 14], tailored for both general and specific data mining tasks, have been proposed based on these privacy models.

However, Wong et al. [15] showed that these algorithms are vulnerable to minimality attack and do not provide the privacy guarantees. Subsequently, more privacy attacks such as composition attack [16], deFinetti attack [17], and foreground knowledge attack [18] have emerged against these algorithms [13, 14].

Differential privacy has received considerable attention recently as a substitute for aforementioned partition-based models for privacy preserving data publishing (PPDP). A differentially-private mechanism ensures that the probability of any output (released data) is equally likely from all nearly identical input data sets and therefore guarantees that all outputs are insensitive to an individual’s data. Most of the research on differential privacy concentrates on non-data publishing with the goal to reducing the magnitude of added noise [19, 20], or releasing certain data mining results [21, 22]. These techniques completely prohibit the sharing of data. When compared to sharing the results of data mining, data sharing gives greater flexibility because recipients can perform their required analyses and data exploration, and apply different modeling methods and parameters.

Current techniques that allow data sharing publish contingency tables of the original data [20, 23–25]. These techniques generally add Laplacian noise to the raw counts of records to ensure differential privacy. The Laplacian mechanism has two main limitations. First, Laplacian noise on counts could eliminate almost half of the small counts, since negative counts are considered as zero. Second, Laplacian noise is unbounded, which could result in released data to be unexpectedly large, and with a few records sampled repeatedly, dominating the entire database. Thus, these techniques may significantly destroy the data utility. We also confirmed this point by experiments in Section 4.

1.2 Contributions

In this paper, we propose two privacy-preserving data publishing (PPDP) mechanisms: differential PCA and differential LDA. The proposed mechanisms build a compact, privacy-preserving synopsis based on component analysis with a fixed amount of privacy budget. Synthetic data are generated from the privacy-preserving synopsis to answer any queries or build data mining algorithms without decreasing the level of privacy protection. Our component analysis based privacy preserving data publishing (PPDP) mechanisms add noise, mostly on the first and second moments (i.e., mean and variance-covariance) rather than on the original data or their contingency tables. This reduces the required amount of noise and enables us to provide the same privacy protection with less perturbation compared to existing techniques. Next, we briefly present the key advantages of the proposed mechanisms.

1. The differential PCA-based PPDP generates synthetic data with a one-to-one mapping to the original data, and preserves the order information. This is essential for data custodians to publish time-series data (i.e., lab tests) or enable privacy preserving sequential release of attributes from the same database.

2. The differential LDA-based PPDP provides great flexibility in generating synthetic data, which provides a better preservation of the original data distribution. Experimental results demonstrated that the proposed LDA-based PPDP outperforms the recently proposed differentially-private data release algorithm [25] for different utility metrics.

A similar mechanism to our PCA-based PPDP called SuLQ [26], which is also based on principle component analysis, however, is different from our work in its purpose (i.e., query in the projected subspace vs. data publishing) and noise addition procedures (i.e., adding Gaussian noise to variance-covariance matrix in SulQ vs. adding Laplacian noise to both variance-convariance matrix and projected data in our case). We are not aware of similar works to our LDA-based PPDP.

The rest of the paper is organized as follows. Section 2 reviews Principle Component Analysis (PCA), Linear Discriminate Analysis (LDA), and Differential Privacy (DP). Our component-analysis based privacy preserving data publishing mechanisms are explained in Section 3. Section 4 experimentally evaluates the performance of our methods and compares to the state-of-the-art models. Section 5 concludes the paper.

2 Preliminaries

Principle Component Analysis (PCA) is an analysis method that converts observations of random vectors into orthogonal principal components, while the number of principal components can be either equal or smaller than the dimension of the original data. When the number of components is smaller than the dimension of the original data, we can project the original data to the space of these principal components to get a low-rank approximation. The idea behind this approximation is to preserve as much information of the original data (i.e., the criterion is to minimize the F-norm of the approximation error) as possible. Mathematically, given a matrix X_n×p representing the n-record and p-dimensional data, PCA decomposes the variance-covariance matrix D = Var [X] = U^TVU, where U is an orthogonal matrix consists of eigenvectors, and

$$V=\mathit{\text{diag}}\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_p\},{\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_p\ge 0$$

are the eigenvalues. The eigenvectors are also called principal components. Suppose U_k is the first k eigenvectors of Var [X], we can get an approximation of X by computing

$$(X-E[X])U_k^T{U}_k+E[X].$$

Based on linear algebra, we know that

$$\parallel (X-E[X])U_k^T{U}_k+E[x]-X{\parallel }_F^2=\frac{{\lambda }_{k+1}+\cdots +{\lambda }_p}{{\lambda }_1+\cdots +{\lambda }_p}\parallel X-E[X]{\parallel }_F^2.$$

For correlated data, the ratio between meaningful eigenvectors and total eigenvectors is usually small, i.e., there exists some k ≪ p $\frac{{\lambda }_{k+1}+\cdots +{\lambda }_p}{{\lambda }_1+\cdots +{\lambda }_p}\simeq 0$.

Linear Discriminant Analysis (LDA) is a classification algorithm based on component analysis. It assumes that data in each class comes from a Gaussian distribution, and it uses the probability density to classify new samples. For example, suppose the data in class C_i have a mean of μ_i and a variance-covariance matrix Σ, then for each new data x, the probability

$$P(x\in C_i)\propto \text{exp}(-\frac{1}{2}\text{log}|\mathrm{\Sigma }|-\frac{1}{2}{(x-{\mu }_i)}^T{\mathrm{\Sigma }}^{-1}(x-{\mu }_i)).$$

To predict the class to which the sample belongs, we just need to compare the probabilities.

Differential privacy (DP) is a cryptographically motivated privacy criterion proposed by Dwork [27], which assumes that any results (i.e., through query operations) of a “private” data set should not drastically change with an addition, deletion, or update of a single record. The Laplacian mechanism is a common way for achieving differential privacy.

Definition 1 (ε-Differential Privacy). A randomized algorithm (or mechanism) Ag is differentially private if for all data sets 𝒟 and 𝒟′, where their symmetric difference contains at most one record, and for all possible anonymized data sets 𝒟̂,

$$\text{Pr}[Ag(𝒟)=\widehat{𝒟}]\le e^{\epsilon }\times \text{Pr}[Ag(𝒟\prime )=\widehat{𝒟}],$$ (1)

where the probabilities are over the randomness of the algorithm Ag.

Theorem 1 [20] (Laplacian mechanism) For any function f : 𝒟 → R, the algorithm Ag that adds noise with distribution Lap(s/ε) (where s = max_{𝒟, 𝒟′} ∥(f(𝒟) − f (𝒟′))∥₁ denotes sensitivity and ε stands for the privacy budget) to the outputs of f (·) satisfies differential privacy.

3 Methodology

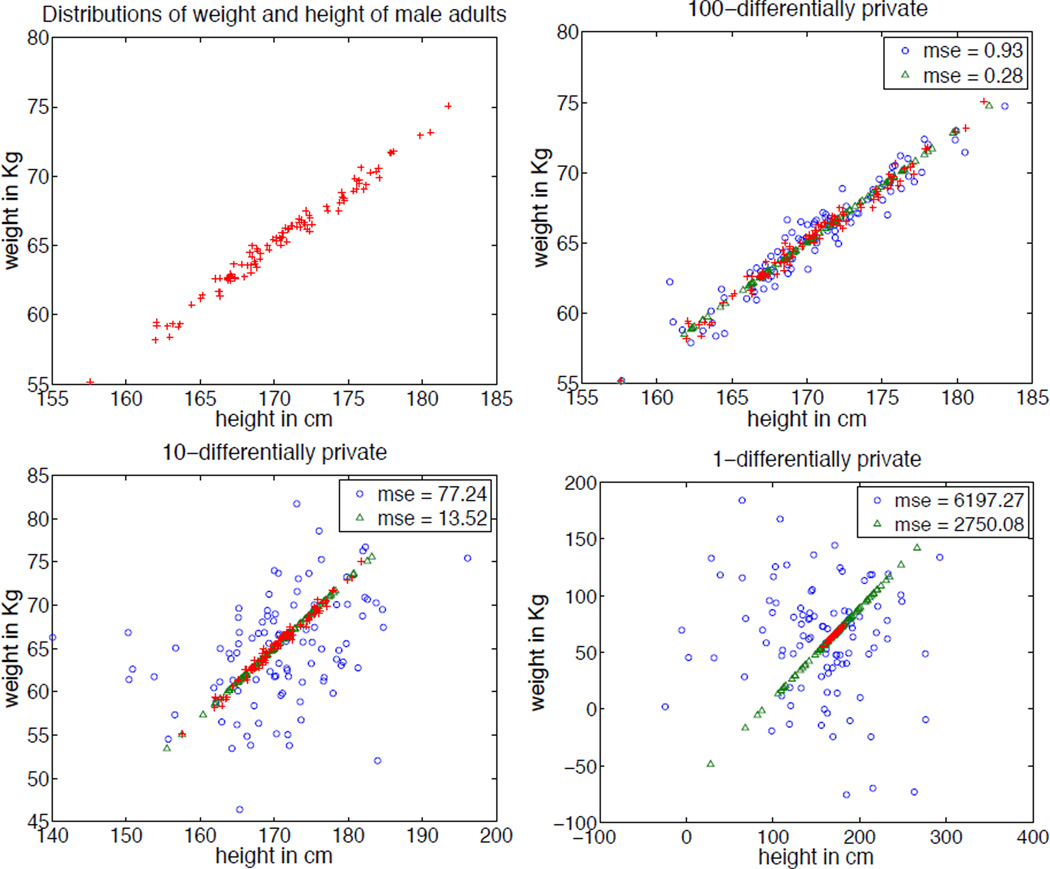
We first illustrate our intuition why component analysis could help. In the simplified example showed in Figure 1, we considered a data set of 100 male adults with two highly correlated attributes: height and weight. Here, we considered the identity query as in [28]. It publishes the data matrix directly instead of some other queries (e.g., count query) that preserves the property of the data set. To ensure privacy for identity query, one should intuitively perturb each data point. Note that since each record can be considered as a disjoint data set, parallel composition [29] holds, and thus we can ensure the entire data set to be ε-differentially private as long as each record is ε-differentially private. However, the height and weight queries do not apply to disjoint sets of record. Therefore, based on sequential composition [29] , we evenly split the ε budget separately into the two attributes for ensuring each of them to be ε/2-differentially private ¹. On the other hand, if the appropriate “component” is picked (i.e., using common knowledge about weight and height), we do not need to split the budget but can use the entire ε for a single dimension. As a result, the mean squared error (MSE) can be significantly reduced. More importantly, as illustrated in the figure, the statistics of the data change drastically if we naively apply noise to each dimension (attribute) independently. This could make the data virtually unusable. In reality, the common knowledge about components does not always exist. Therefore, it is necessary to use component analysis to find the major components so that noise is added to fewer but most important “parts” of data without decreasing the level of privacy protection. In this paper, all the expectations mean empirical expectation. A replace of sample will not change the expectations on the underlying distribution, but it does change the empirical expectation.

Figure 1.

Two versions of noisy data after applying the Laplacian mechanism to: (1) a principal component (noisy results indicated by ‘Δ’), (2) the original domain (noisy results indicated by ‘o’), of simulated weight and height data of male adults (’+’). The difference of mean squared errors (MSE) between component aware and unaware approach increases as the privacy budget decreases. For example, for privacy budget, ε = 1, the difference is (6197.27 − 2750.08) as shown in the lower-right figure. Our interested ranges for both weight and height were predetermined before getting the data, therefore, sensitivity is independent of the data.

3.1 Differential PCA

In differentially PCA, we add noise in both projection and recovery steps as mentioned in Section 2. First, we decompose a noisy variance matrix instead of the exact matrix. Second, we add noise to the projected matrix before recovery. Suppose the samples are p-dimensional i.i.d. random vectors X₁, X₂, …, X_n, this mechanism guarantees better better performance than the Laplacian mechanism (i.e., on the raw data) in terms of F-norm, if nε ≫ p² and ε² + k² ≤ p² (the latter is often true since we usually have k < p and small ε).

Both conditions will be justified in Theorem 3 but let us first discuss how to get differentially private E [X] and upper triangle E [XX^T] from X, which are essential to this mechanism. Specifically, we only consider the upper triangle of E [XX^T] because of its symmetry, i.e., if we change its upper triangle, we can just copy the noisy entries to the lower triangle.

Suppose each variable is clamped to [0, 1], and there are p numerical variables in total, the sensitivity of Σ_x∈X x and upper triangle Σ_x∈X xx^T are s = p + (p + 1)p/2. The detailed differential PCA is as follows. (The mechanism for data set with categorical variables will be discussed later).

PCA-based PPDP Mechanism

1. Given a data set (or matrix) X_{n × p}. Suppose each entry in the set is bounded to [0, 1], we compute Σ_x∈X x and Σ_x∈X xx^T.

2. Get noisy sums of x and xx^T by adding Lap(2s/ε) on each entry of Σ_x∈X x and upper triangle of Σ_x∈X xx^T, then fill in the lower triangle of Σ_x∈X xx^T with the upper triangle symmetrically.

3. Get E[X]_noisy and E[XX^T]_noisy by dividing the noisy sums by sample number n.

4. Step 3 ensures that

   $$\overline{D}=E{[X{X}^T]}_{\mathit{\text{noisy}}}-E{[X]}_{\mathit{\text{noisy}}}E{[X]}_{\mathit{\text{noisy}}}^T$$

   is a symmetric matrix. Thus, we can eigen-decompose it D̅ = U̅^T V̅ U̅, and select the k ≤ p eigenvectors that have the largest eigenvalues from U̅ to form U̅_k.

5. Add noise $Lap(2\sqrt{kp}/\epsilon )\text{on}(X-E{[X]}_{\mathit{\text{noisy}}}){\overline{U}}_k^T$, multiply it by U̅_k, and add E[X]_noisy to each sample to get noisy X̅.

Proof of differential privacy

Lemma 1 E[X]_noisy and E[XX^T]_noisy are ε/2-differentially private.

Proof. The sum of sensitivities of Σ_x∈X x and Σ_x∈X xx^T is s, thus the noisy sums in the second step are ε/2-differentially private, and so are E[X]_noisy and E[XX^T]_noisy in the third step.

Lemma 2 Given ${\overline{U}}_k^T$, the sensitivity of $(X-E{[X]}_{\mathit{\text{noisy}}}){\overline{U}}_k^T\text{is}\sqrt{kp}$.

Proof. Since $X{\overline{U}}_k^T$ is an n × k matrix, and each sample only affects one row in it, we only need to prove that for any x₁ and x₂ there is

$$\parallel (x_1-x_2){\overline{U}}_k^T{\parallel }_1\le \sqrt{kp}$$

Since there are k orthogonal components in U̅_k which are all unit length vectors, we can use u₁ to u_k to represent them. The maximum value of $\parallel (x_1-x_2){\overline{U}}_k^T{\parallel }_1$ is max ${\sum }_{i=1}^k\left|{(x_1-x_2)}^T{u}_i\right|$. Since

$${(\sum _{i=1}^k|{(x_1-x_2)}^T{u}_i|)}^2\le k\sum _{i=1}^k|{(x_1-x_2)}^T{u}_i{|}^2\le k\parallel x_1-x_2{\parallel }_2^2\le kp,$$

the maximum value is therefore less than $\sqrt{kp}$.

Lemma 3 The noise added $(X-E{[X]}_{\mathit{\text{noisy}}}){\overline{U}}_k^T$ is also ε/2-differentially private.

Proof. In step 5 of the PCA-based PPDP mechanism, we add noise $Lap(2\sqrt{kp}/\epsilon )\text{to}(X-E{[X]}_{\mathit{\text{noisy}}}){\overline{U}}_k^T$ (i.e., which has a sensitivity of $\sqrt{kp}$), therefore making it ε/2-differentially private.

Theorem 2 The differential PCA mechanism is ε-differentially private.

Proof. For any data sets 𝒟₁ and 𝒟₂ that differ at most one entry, we have (suppose the data matrix in 𝒟₁ is X₁ and that in 𝒟₂ is X₂)

$$\left|\frac{P(\overline{X}|X_1)}{P(\overline{X}|X_2)}\right|=\left|\frac{\int P(\overline{X}|E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}},X{\overline{U}}_{k(\mathit{\text{noisy}})}^T)P(E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}},X{\overline{U}}_{k(\mathit{\text{noisy}})}^T|X_1)}{\int P(\overline{X}|E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}},X{\overline{U}}_{k(\mathit{\text{noisy}})}^T)P(E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}},X{\overline{U}}_{k(\mathit{\text{noisy}})}^T|X_2)}\right|\le \underset{E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}},X{\overline{U}}_{k(\mathit{\text{noisy}})}^T}{\text{max}}\left|\frac{P(E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}},X{\overline{U}}_{k(\mathit{\text{noisy}})}^T|X_1)}{P(E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}},X{\overline{U}}_{k(\mathit{\text{noisy}})}^T|X_2)}\right|\le \underset{E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}},X{\overline{U}}_{k(\mathit{\text{noisy}})}^T}{\text{max}}\left|\frac{P(X{\overline{U}}_{k(\mathit{\text{noisy}})}^T|E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}},X_1)P(E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}}|X_1)}{P(X{\overline{U}}_{k(\mathit{\text{noisy}})}^T|E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}},X_2)P(E{[X]}_{\mathit{\text{noisy}}},E{[X{X}^T]}_{\mathit{\text{noisy}}}|X_2)}\right|\le \text{exp}\left(\frac{\epsilon }{2}\right)\text{exp}\left(\frac{\epsilon }{2}\right)=\text{exp}(\epsilon ).$$

Theorem 3 Differential PCA based PPDP adds smaller noise compared to the Laplacian mechanism in terms of F-norm, given: (1) nε ≫ p²; (2) ε² + k² < p².

Proof. The noise of this method comes three ways: approximation of p-dimension data with projection on k-dimensional space, the noise on the variance-covariance matrix D, and on $X{\overline{U}}_k^T$. The first is $\frac{{\lambda }_{k+1}+\dots +{\lambda }_n}{{\lambda }_1+\dots +{\lambda }_n}\parallel X-E[X]{\parallel }_F=\frac{{\lambda }_{k+1}+\dots +{\lambda }_n}{{\lambda }_1+\dots +{\lambda }_n}O(pn)$. The second part is very small when nε ≫ p² because the sensitivity is at most O(p²=nε). When nε ≫ p², the difference between D and D̅ are small, thus the approximation error is also small. The third part is the main source of noise. Its variance is about O(k² pn/ε²) (kn entries, each added noise $Lap(\sqrt{kp}/\epsilon )$ has variance O(kp/ε²)). The noise of the Laplacian mechanism is O(p³n/ε²) (pn noise, each Lap(p/ε)). Thus, our method is better by F-norm when

$$\frac{{\lambda }_{k+1}+\dots +{\lambda }_n}{{\lambda }_1+\dots +{\lambda }_n}O(pn)+O(k^{2}pn/{\epsilon }^2)\le O(p^{3}n/{\epsilon }^2).$$

That is, if $\frac{{\lambda }_{k+1}+\dots +{\lambda }_n}{{\lambda }_1+\dots +{\lambda }_n}\le 1$ is always true and ε² + k² < p², our method adds smaller noise.

How to deal with categorical variables

Although PCA was developed for numerical variables, we can use them for categorical variables. Suppose there are p₁ numerical variables which have been normalized to [0, 1], and p₂ categorical ones. We followed the common practice to change them into dummy variables, and treat these dummy variables as numerical variables in the PCA.

There are two differences introduced by categorical variables. First, the sensitivity is significant lower. Although one categorical variable may generate many dummy variables, only one of them can be one in a sample, and the others are all zeros. The largest change of Σ_x∈X x and upper triangle of Σ_x∈X xx^T is achieved by changing all numerical variables from zero to one (or from one to zero), and all categorical ones at the same time. In this case, p₂ (or p₁ + p₂) values are changed from one to zero and p₁ + p₂ (or p₂) are changed from zero to one. Thus Σ_x∈X x changes with (p₁ + 2p₂) in terms of L₁ norm, and the upper triangle of Σ_x∈X xx^T changes with [(p₁ + p₂) (p₁ + p₂ + 1) + p₂(p₂ + 1)]/2. Therefore, the sensitivity s of (Σ_x∈X x, upper triangle of Σ_x∈X xx^T) is (p₁ + 2p₂) + [(p₁ + p₂)(p₁ + p₂ + 1) + p₂(p₂ + 1)]/2. Note that the number of different values of one variable does not contribute to the sensitivity.

The second difference comes from the value recovery. Since the noisy outputs are continuous, it is necessary to recover the categorical variables from dummy variables. In differential PCA, the recovery is simply picking the largest value of noisy outputs so that one category is selected. In this way, the output can keep the same format (i.e. categorical) as the input.

3.2 Differential LDA

This mechanism aims at preserving as much information as possible for classification algorithms instead of the original data, which makes it different from the first mechanism.

As the LDA only uses the means and variance-covariance matrices (here we assume that all classes have the same variance matrix to reduce sensitivity) of data in different classes, we must preserve as much information on them as we can. Our idea is first to get these noisy statistics, and then generate data from them. Suppose there are two classes (in fact, it can be generalized to multi-class classification easily). Assume all the p variables are numerical variables in [0, 1], the mechanism is elaborated as follows:

LDA-based PPDP Mechanism

1. Given data set (or matrix) X_n×p for classes i = 1,2 and suppose each entry in the set is clamped to [0, 1]. We obtain Σ_x∈Classi x and Σ_{x∈both class} xx^T.

2. Add noise Lap([2p + p(p + 1)/2]/ε) on noisy sums and then divide them by sizes of two classes and the whole data set to get E_i[X]_noisy, i = 1, 2 and E[XX^T]_noisy. The E[XX^T]_noisy shall be symmetric by the same method in PCA (add noise on the upper triangle and copy values to the lower triangle).

3. Draw samples that approximately minimize the L₁ distance between their statistics and the noisy statistics. The detail of this sampling procedure will be provided later.

In experiments, the sampling algorithm not only generates new data in the original format, but also reduces the noise in the noisy statistics. Note that publishing the samples offers better utility than publishing the noisy statistics.

Proof of Differential Privacy

The key is to prove the noisy statistics in step 2 are differentially private. The replacement can happen in one class or between classes. If the replacement is within one class, then the proof for the differentially private PCA also works here. If one sample s₁ in Class 1 is replaced by a sample s₂ in Class 2, the change of E_i[x], i = 1, 2 are as follows. Suppose the two classes are denoted X₁ and X₂, and have n₁ and n₂ samples originally. Then the statistics changes from

$$\frac{1}{n_1}\sum _{x\in X_1\cup \{s_1\}}x\text{and}\frac{1}{n_2}\sum _{x\in X_2}x$$

to

$$\frac{1}{n_1-1}\sum _{x\in X_1}x\text{and}\frac{1}{n_2+1}\sum _{x\in X_2\cup \{s_2\}}x.$$

The L1 norms of the changes of the two statistics are

$$|\frac{1}{n_1}\sum _{x\in X_1\cup \{s_1\}}x-\frac{1}{n_1-1}\sum _{x\in X_1}x{|}_1\le \text{max}\{|\frac{1}{n_1(n_1-1)}\sum _{x\in X_1}x{|}_1,|\frac{1}{n_1}{s}_1{|}_1\}\le \text{max}\{\frac{p}{n_1},\frac{p}{n_1}\}=\frac{p}{n_1}|\frac{1}{n_2}\sum _{x\in X_2}x-\frac{1}{n_2+1}\sum _{x\in X_2\cup \{s_2\}}x{|}_1\le \text{max}\left\{\right|\frac{1}{n_2(n_2+1)}\sum _{x\in X_2}x{|}_1,\left|\frac{1}{n_2+1}{s}_2{|}_1\right\}\le \text{max}\{\frac{p}{n_2+1},\frac{p}{n_2+1}\}=\frac{p}{n_2+1}.$$

If a sample in the second class is replaced by a sample in the first class, the changes are bounded by $\frac{p}{n_1+1}\text{and}\frac{p}{n_2}$. As the noise added to the sums are Lap([2p + p(p + 1)/2]/n₁ε) and Lap([2p + p(p + 1)/2]/n₂ε) respectively, the two statistics are at least 2ε/(p + 5) differentially private each.

As the largest change of upper triangle of Σ_{x∈both class} xx^T is still p(p + 1)/2 and the noise added to each component of the upper triangle is Lap([2p + p(p + 1)/2]/ε), the noisy covariance matrix (after divided by n₁ + n₂) is at least (p + 1)ε/(p + 5)-differentially private. Therefore, the three statistics are 2ε/(p + 5), 2ε/(p + 5) and (p + 1)ε/(p + 5) differentially private, respectively. The combination of them preserves ε differential privacy.

Since the statistics in step 2 of this mechanism are ε differentially private, and the algorithm does not use the original data in the following steps, this algorithm preserves ε differential privacy.

Sampling

As the LDA depends on the inverse of covariance matrix and the noisy matrix might contain negative elements, the noisy statistics cannot be used in classification directly. One solution is to eigen-decompose the matrix and change all the eigenvalues to be positive, however, its performance might be undermined. We want the output data useful for meaningful tasks, for example, classifiers. Therefore, it is necessary to draw samples from the noisy statistics.

Our sampling procedure is to reduce the noise (i.e., in the statistics) by rectifying some projected errors introduced in the previous steps for maintaining differential privacy. We treat the sampling as an optimization problem, which aims at minimizing the following target function (i.e., equals to maximizing the likelihood):

$$Y={\text{argmin}}_{{\{y_j\}}_{j=1,\dots ,n}}\sum _i{\left|\sum _{y_j\in \left|\text{Class}i\right|}{y}_j-n_i{E}_i[x]\right|}_1+{\left|\sum _{y_j}{y}_j{y}_j^T-(n_1+n_2)E_{[x\in \text{both class}]}[x{x}^T]\right|}_1.$$

We use a greedy algorithm to solve this problem iteratively, and each sample is obtained in one iteration. In each iteration, one of the two classes are chosen, then the sample approximately minimizing the target function is calculated (in the target function, the three noisy statistics E_i[X]_noisy, i = 1, 2 and E[XX^T]_noisy are multiplied by the number of samples obtained so far instead of n₁ and n₂).

To get a sample, we calculate features one by one using the greedy algorithm. When choosing the best value z for one feature, we have p + 1 items related to z in the target function. Among them, there is 1 item like |z − z₀| in the first item of target function, 1 item like |z² − z₁| and p − 1 items like |z₂z − z₃| in the second items (here z₀, z₁ and z₃ are pre-determined constants, and z₂ is other feature’s value). The first step is to change all items to the form of |az − b| (a and b are constants). We replace the z² in |z² − z₁| by the product of z and its noisy mean, and replace all z₂ with constants in this way: if the corresponding value has been got, then that value will replace z₂; if the corresponding value has not been decided, the noisy mean will replace z₂. As the target function reduced to sum of functions like |az − b|, which is piecewise linear, one of zero points of those az − b = 0 must be the optimal value, therefore, only the target function on those zero points shall be compared (if there are other constraints on the value, they can be considered in the selection here. For example, if the values must be in [0, 1], then 0 and 1 may also be the optimal value). Therefore, we just use O(p) time to get O(p) possible optimal values and O(p²) time to get the target function for them and select the true optimal. As there are p features in a samples, O(p³) operations are needed in each iteration. Experiments show that the statistics of the samples are closer to the true statistics than the noisy statistics, which validates the usefulness of this method.

Categorical variables

The categorical variables also bring two challenges to LDA after we convert them to dummy variables. The first is sensitivity. With p₁ numerical variables and p₂ categorical variables, the sensitivity of E_i [x], i = 1, 2 are (p₁ + p₂)=n₁ and (p₁ + p₂)/n₂, and the sensitivity of the upper triangle of E_{x∈both class} [xx^T] is bounded by [(p₁ + p₂ + 1)(p₁ + p₂) + p₂(p₂ + 1)]/2(n₁ + n₂). Therefore by the similar analysis as above, it’s easy to prove that to add noise Lap({2(p₁ + p₂) + [(p₁ + p₂ + 1)(p₁ + p₂) + p₂(p₂ + 1)]/2}/ε) to each component of the sums preserves ε differential privacy.

The second problem is sampling. The main idea is still the same as used in the numerical variables situation, but the complexity is lower than O(p³). Suppose that there are K possible values for a categorical feature, only K possible values shall be tested for the K dummy variables as only one of them can be 1, and each value’s target function still needs O(p) time. The time complexity to choose the best value for this categorical value is at most O(K_p). As there are p variables including dummy variables in total, the number of all dummy variables is less than O(p²). If the categorical variables are chosen before numerical variables, to select the numerical variables need only O(p₁(p₂ + p₁)²) time. Therefore the time complexity for each sample is O(p² + p₁(p₂ + p₁)²). When there are a lot of dummy variables (p >> p₁ + p₂), this sample algorithm has about the same time complexity as computing LDA’s variance matrix, O(p²).

4 Experiments

In this section, we first compared differential PCA with the Laplacian mechanism [20] and Exponential mechanism [30] in terms of F-norm of the introduced noise (i.e., cumulative mean squared errors). The utility function q for the baseline Exponential mechanism is defined as the one used in [31]. Regarding differential LDA, which aims at preserving information for classification, we compared it with DiffGen [25], a state-of-the-arts data publishing mechanism that preserves classification information.

4.1 Data sets

We used the adult data set from UCI machine learning repository [32]. It is the US census data of 1994, which contains 45,222 records. Each corresponds to a person. In each record, there are 15 features on the person’s gender, education level, race, nationality, job, income, etc. The first 14 features are often used to predict the last one (i.e., whether this person earned more than $50k per year).

Since there are a lot of categorical values (i.e., nationality, zipcode, and etc.) in the data set (the number of unique categories from all categorical attribute values is about 22,000), there can be severe over-fitting and the Laplacian noise can be large (i.e., when we introduce dummy variables, the scales of the noise are in the order of square of total unique values). Therefore, we removed features: final weight, education, occupation and nationality, and used dummy variables to represent the rest of the categorical variables. Since our mechanisms require the data to be in [0, 1], we normalized the continuous variables. After these pre-processing, there were 35 features remaining.

4.2 Design

All the dummy variables are binary in the original data. However, we cannot add Laplacian noise directly to them. Therefore, we treated them as real-numbered variables and expanded their domains to R. Although the data in each class were not from a normal distribution even if we expanded the domain, we can still use the LDA mathematically. This data-independent use of LDA is also required in practice because if we only use the mechanism when data are normally distributed, it may leak some information about the data.

4.3 Differential PCA Results

We evaluated our differential PCA-based PPDP by F-norm and compared results with those of Laplacian and Exponential mechanisms. The same experiments were repeated 10 times, and we reported the average performance of all three mechanisms in Figure 2.

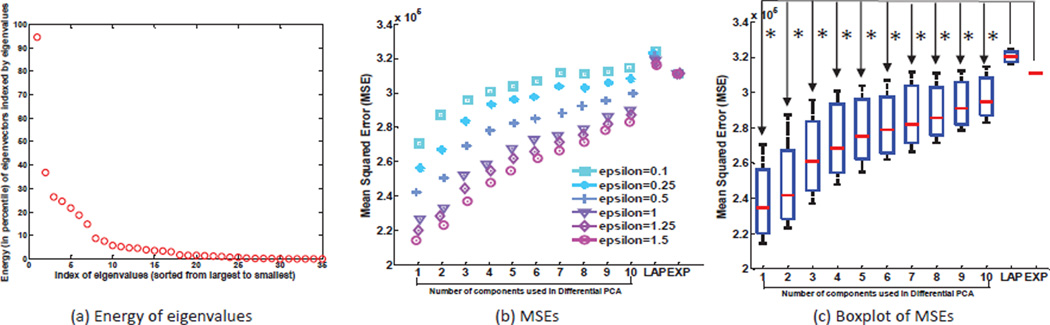
Figure 2.

Differential PCA is compared to Laplacian (LAP) and Exponential (EXP) mechanisms in terms of the F-norm, i.e., Cumulative mean squared errors (MSE). (a) Energy in percentile carried by eigenvectors sorted by their eigenvalues. (b) Comparison of MSEs between three mechanisms at six different privacy budgets, i.e., ε = 0.1, 0.25, 0.5, 1, 1, 25, 1.5. (c) Boxplots of MSEs. In (b) and (c), we implemented differential PCA-based PPDP with various numbers of components (i.e., 1–10), and all results are averaged from 10 trials. T-test shows that MSEs of PCA are significantly smaller than those of LAP and EXP and PCA (p < 0:01), indicated by stars.

The first subfigure indicates that the top 10 eigenvectors carried more than 90% of the entire energy of the data, and there is not much information left for the rest of the eigenvectors. As opposed to the ordinary PCA, the mean squared errors for the differential PCA increase rather than decrease when more components were used, which implies the noise required for satisfying differential privacy overshadows information carried by additional components.

The second and third subfigures show differential PCA-based PPDP has a clear advantage over Laplacian and Exponential mechanisms, and such differences are statistically significant based on Student-t tests. Indeed, differential PCA outperformed the other two methods in the entire range of component sizes (i.e., k = 1 to 10). Note that we used the strategy introduced in Section 3.1 to convert numerical variables back to categorical ones in order to make the outputs look reasonable.

4.4 Differential LDA Results

4.4.1 Classification performance

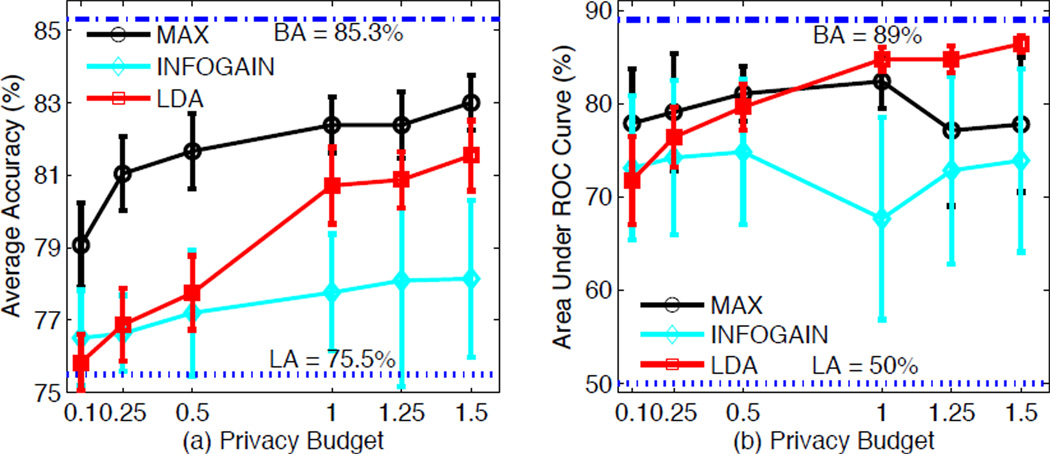
In the first part of this section, we compared the proposed differential LDA with other two data publishing mechanisms targeted at preserving classification information, i.e., DiffGen-INFOGAIN and DiffGen-MAX [25]. First, we use the output of both diffential LDA, DiffGen-INFOGAIN and DiffGen-MAX to train a LDA classifier model and a C4.5 classifier model, respectively. Second, we compare their classification performance in terms of average classification accuracy (ACA) and area under the ROC curves (AUC) based on 10 trials, where we used 2/3 of the records to generate training data and the remaining 1/3 of the records to test the classification performance. To better visualize the performance of the mechanisms, we provide additional measures: error bar is the standard deviation of each data point based on 10 trials, best achievable (BA) and lowest achievable (LA) performances are the best and lowest possible performances of ACA and AUC measurements given original data or completely generalized data [25], respectively.

Figure 3(a) depicts the ACA among three different methods (i.e., DiffGen-INFOGAIN, DiffGen-MAX, and LDA) with the privacy budget ε = 0.1, 0.25, 0.5, 1, 1.25, 1.5. In addition, BA and LA accuracies are 85.3% and 75.5%, respectively. In Figure 3(a), we can see that the ACA of all three methods increases as the privacy budget increases. Moreover, the ACA of the proposed method outperforms that of DiffGen-INFOGAIN given the privacy budget ε ≥ 0.25, although it is still slightly lower than the ACA of the DiffGen-MAX at high privacy budgets. Furthermore, Figure 3(a) also shows that both the proposed method and DiffGen-MAX have significantly smaller standard deviations compared to these of the DiffGen-INFOGAIN. Next, in Figure 3(b), the AUC performances are also studied to measure the classification performance of the three different anonymization methods. The AUCs of the proposed method are clearly higher than these of the other two methods, when the privacy budget is larger than 0.5. More important, our proposed method always offers the lowest standard deviation for all different budgets among all three methods. The experimental results suggested that the proposed differential LDA method achieves a comparable ACA with DiffGen-MAX, but higher AUC on average and a lower AUC standard deviation.

Figure 3.

Comparison of (a) the average accuracy and (b) average AUC between DiffGen-INFOGAIN, DiffGen-MAX, and LDA. BA: best achievable; LA: lowest achievable.

4.4.2 Information preservation

In the second part, we also compared all the three methods in terms of information preservation. We measure the preserved information of these mechanisms by two information theoretic metrics: entropy and Kullback-Leibler (KL) divergence [33]. In Information Theory, the entropy provides a measure of how much information the data contain. A larger entropy for the released data implies a greater amount of information that a released data might contain, however, does not indicate how relevant such infromation is about the original data. The KL divergence (a.k.a. relative entropy) was introduced to measure the difference D_KL(P∥Q) between the distribution of released data P and that of the original data Q, where D_KL (P∥Q) is a non-negative metric with D_KL(P∥Q) = 0 if and only if P = Q.

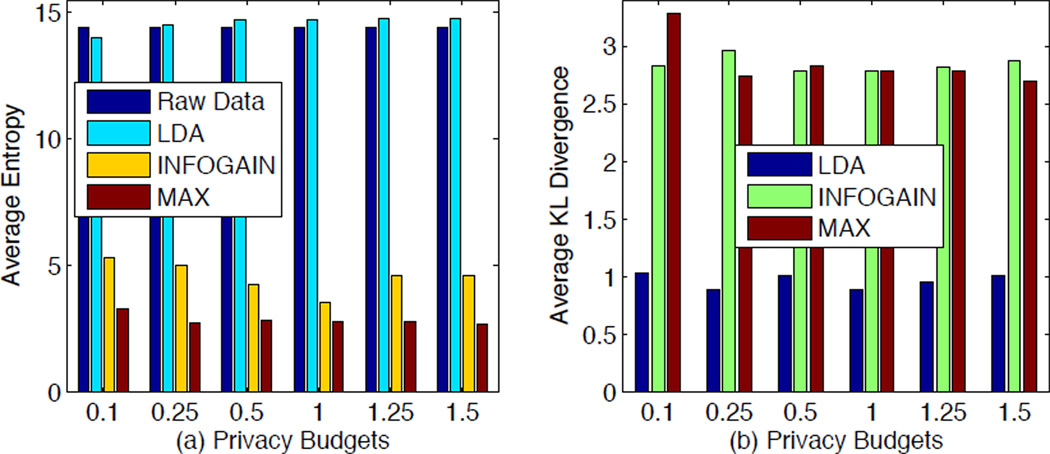
Figure 4(a) shows the entropies of released data by using DiffGen-INFOGAIN, DiffGen-MAX and the proposed differential LDA, where the entropy of original data is given as a reference. We can see that the entropy obtained by the proposed method is similar to that of the original data, whereas the entropies of the other two methods (i.e., DiffGen-INFOGAIN and DiffGen-MAX) are quite lower than that of the original data. In other words, the amount of information preserved by our proposed anonymization method is comparable to that of the original data, while the amount of released information in DiffGen-INFOGAIN and DiffGen-MAX methods are only about 30% and 20% of the original data, respectively. These results indicate that both the DiffGen-INFOGAIN and DiffGen-MAX methods merely intend to preserve useful information for classification purpose. In contrast, the proposed method could preserve an equivalent amount of information as the original data, which offers greater usability for general-purpose data mining tasks other than classification.

Figure 4.

Comparison of the capability of information preservation among DiffGen-INFOGAIN, DiffGen-MAX, and LDA: (a) the average entropy of released data; (b) the average KL divergence between released data and the original data.

Second, in Figure 4(b) we investigated how the released information from different anonymization methods is relevant to the original data, in terms of KL divergence. Figure 4(b) shows that the proposed method achieves the minimum average KL divergence among all three anonymization methods, where the KL divergence of the proposed method is only about one thirds of the other two methods. This shows that differential LDA outperforms the other two methods, as it maintains a more similar distribution in the released data, as well as preserves a larger amount of information.

5 Conclusions

In this paper, we proposed two novel mechanisms for privacy preserving data publishing that achieve ε-differential privacy and provide better utility than the existing techniques. Two mechanisms, differential Principle Component Analysis and differential Linear Discriminant Analysis were studied in this paper. The former method serves as a general-purpose data dissemination tool that guarantees better utility (i.e., lower error) when compared to Laplacian and Exponential mechanisms, that use the same privacy budget. The method is applicable to data dissemination for classification purposes. Through theoretically justification and experimental comparisons, we showed that the proposed privacy preserving data publishing mechanisms are more effective than the state-of-the art alternatives in retaining data utility.