Longitudinal data analysis with non-ignorable missing data

Abstract

A common problem in the longitudinal data analysis is the missing data problem. Two types of missing patterns are generally considered in statistical literature: monotone and non-monotone missing data. Non-monotone missing data occur when study participants intermittently miss scheduled visits, while monotone missing data can be from discontinued participation, loss to follow-up and mortality. Although many novel statistical approaches have been developed to handle missing data in recent years, few methods are available to provide inferences to handle both types of missing data simultaneously. In this article, a latent random effects model is proposed to analyze longitudinal outcomes with both monotone and non-monotone missingness in the context of missing not at random (MNAR). Another significant contribution of this paper is to propose a new computational algorithm for latent random effects models. To reduce the computational burden of high dimensional integration problem in latent random effects models, we develop a new computational algorithm that uses a new adaptive quadrature approach in conjunction with the Taylor series approximation for the likelihood function to simplify the E step computation in the EM algorithm. Simulation study is performed and the data from the Scleroderma lung study are used to demonstrate the effectiveness of this method.

1 Introduction

Longitudinal study designs are frequently used in clinical studies to monitor disease progression and treatment efficacy over time. One of the most common problems in the longitudinal data analysis is the missing data problem. During the course of study, the outcomes of interest can be missing due to subjects’ non-response, missed visits, dropout, death and other reasons. There is a rich statistical literature on the analysis of missing data¹. If the missingness is independent of the observed and unobserved data, the missing mechanism is missing completely at random (MCAR). If given the observed data, the missingness is independent of unobserved data, it is defined as missing at random (MAR). For data of MCAR and MAR, the missing mechanisms are considered as ‘ignorable’ missingness, and likelihood methods provide valid inference without modeling the missing mechanisms. However, in practice it may be difficult to justify the independence assumptions of MCAR or MAR, and we need to consider missing not at random (MNAR), where the missing probability depends on unobserved data. For example, in our motivated example of the Scleroderma lung study, about 60% of patient dropouts are due to death and treatment failure, which are likely related to the lack of treatment efficacy.

In statistical literature, two types of missing data patterns are generally considered². The first type is called ‘intermittently missing’ or ‘non-monotone missing’, where a subject may miss particular visits during the course of study follow-up and return at later scheduled visits. On the other hand, “monotone missing” data refer to that a subject may leave the study at some point and never return. Most statistical models focus on one type of missing data pattern. For example, to handle non-monotone and non-ignorable missing data³, a full likelihood approach has been used to specify the joint likelihood of the outcome and missing indicator. Others^4,5 suggested the use of the pseudo likelihood approach for the analysis with non-monotone missing data. On the other hand, different methods⁶ are developed to handle monotone missing data. In reality, we often observe both types of missing patterns simultaneously in longitudinal studies.

In this paper we are interested in making statistical inference with both monotone and non-monotone missing data in longitudinal studies, assuming MNAR. We use the joint model approach to model longitudinal outcomes, intermittent missing data and patient death or treatment failure simultaneously. For example in the Scleroderma lung study, we will use a linear mixed effects model to characterize the longitudinal forced vital capacity (FVC) outcome, a logistic mixed effects model for the intermittent missing data, and a proportional hazards frailty model for the time to dropouts due to death or treatment failure. The correlations of the random effects in the three models represent the unobserved dependence among the longitudinal outcome, intermittent missingness, and time to death or treatment failure. This approach allows to access the dependence between missingness and longitudinal outcomes, to correct the bias in estimation due to missed visits, patient death or treatment failure, and to improve the efficiency of parameter estimation by using all available information.

Despite the advantages of the joint model approach, the computation of the joint model remains challenging due to its large number of parameters included in the models and high dimensional latent variables to capture the dependence among all observations. Many authors^7,8 employed the Bayesian approach and used the Markov chain Monte Carlo (MCMC) to estimate the posterior distribution of the parameters. MCMC method provides a straightforward approach to parameter estimation. However, MCMC is computationally expensive, difficult to determine convergence, and necessary to specify prior distributions. On the other hand, the EM algorithm is a popular frequentist approach in the joint model analysis⁹. However the computation in the E step may involve high dimensional integration if the number of random effects is large. Many computation strategies have been proposed to improve the computational efficiency for the estimation in joint models or high dimensional integration in general. For example, the Laplace method^10-13 has been used to approximate the likelihood function to avoid high dimensional integration. Although many found satisfactory results using the Laplace approximation, others^14,15 suggested poor performance of the Laplace approximation. Additional drawbacks of Laplace approximation include that it demands a larger number of repeated measurements for good approximations, and there are no feasible ways to control the approximation accuracy¹³. Alternatively, the adaptive Gaussian quadrature^16,17 and the sparse quadrature¹⁸ provided means to reduce the computational burden and to improve the computational efficiency in high dimension integration.

In this paper, we develop a new computational strategy for the high dimension integration in the E step of EM algorithm. This new approach seeks to reduce the number of evaluations in two ways. First, the adaptive Gaussian quadrature integration makes use of the moment estimates of random effects in the previous EM iteration to construct the importance distribution. Second, we use the Taylor series expansion to approximate the integration in the E steps based on the current moment estimates of random effects. These two techniques effectively reduce the computational burden in the EM steps.

1.1 Relationship to current literature

Our proposed model is an extension of Elashoff et al.¹⁹, which used the latent random effects model to handle non-ignorable monotone missing data. Most missing data literature solely devotes to one type of missing data pattern^3-6. However, both monotone and non-monotone missing data are often observed simultaneously in longitudinal studies. Our model is also similar to Wu et al.²⁰, who considered a nonlinear mixed-effects model for the longitudinal outcome, the proportional hazards model for the time-to-event outcome, and a logistic regression model for missing data. The interpretation of our model emphasizes on handling different types of non-ignorable missing data, whereas Wu et al.²⁰ highlighted the simultaneous modeling a longitudinal outcome and a time-to-event outcome. To characterize the dependence among outcome and different types of missing data, we assume that each outcome model and missing data model has its own random effects and jointly these random effects follow a multivariate normal distribution. Wu et al.²⁰ introduced single random effect that is shared by the longitudinal, time-to-event, and missing data models, with a scalar multiplying each random effect to account for the fact that the linear predictors in each model are measured on different scales and it is not reasonable to assume they have the same variance. The shared random effect model is more restricted that it only allows positive correlations between two outcomes²¹. It has some unexpected consequence such as the marginal distribution to be always overdispersed. Our multivariate random effects represent a more flexible correlated random effects model, which allows a full range of covariance and is a generalization of the shared parameter model in Wu et al.²⁰.

In this paper, we present a new computation strategy to reduce the computation burden on high dimensional integration in the EM algorithm. An efficient method will achieve same accuracy in integration with fewer numerical evaluations. The adaptive quadrature method^16,17 can be viewed as a deterministic version of importance sampling, and the Laplace method is generally used to find a Gaussian density as the importance distribution with the same mode and curvature of the posterior distribution. However, the Laplace method may not be feasible in a multiple level random effects model, while the moment estimates are always available. Naylor et. al²² and Rabe-Hesketh et. al²³ estimated mean and variance of the importance distribution in the context of Newton-Ralphson iteration in searching for maximum likelihood estimates. We use a Gaussian distribution with the same first two moments of the random effects as the importance distribution for adaptive quadrature. To further reduce the number of evaluations in integration, the Taylor series approximation is used for the integrals of complex functions. Others^13,24 have proposed to approximate integrals through the moment generating function in the context of Laplace approximations. Due to the Taylor series approximation, we only need to evaluate the first two moments of the random effects, and we use the same importance distribution to obtain all the first two moments estimates to reduce the effort in searching for importance distributions.

The rest of the paper is organized as follows. In section 2, we present the model specification, the inference procedure and the description of adaptive Gaussian quadrature in the EM steps. Section 3 demonstrates the method with a real example from a Scleroderma clinical trial. In section 4, we conduct simulation studies to examine the effectiveness and the proposed method. We provide the conclusions in section 5.

2 The Joint Model

In this section, we formulate the joint model for non-ignorable missing data with both monotone and non-monotone missingness. Let Y_ij ∈ ℝ be the repeated measurement outcome of the ith subject at visit j, and M_ij be the intermittent missingness indicator of the ith subject at visit j, where M_ij=1 if Y_ij is missing, and M_ij=0 if Y_ij observed. i = 1, …, N and j = 1, …, K; N is the number of subjects and K is the total number of visits. LetS_i = (T_i, δ_i) denote the dropout data on the ith subject. T_i = min(T_Fi, T_Ci) is the minimum of failure time (T_Fi) and censoring time (T_Ci), and δ_i takes value in (0, 1), with δ_i = 0 being a censored event and δ_i = 1 indicating that subject i drops out for reasons associated with unfavourable outcomes, such as death or treatment failure.

In this model Y_ij is missing when M_ij=1 or the subject drops out before the jth visit. Both Y_ij and M_ij are censored by failure/censoring time T_i.

We use a linear mixed effects model for the repeated measurement Y_ij,

$$Y_{ij}=X_{1ij}{\beta }_1+Z_{1i}{b}_{1i}+\sigma {∊}_{ij},$$ (1)

where X_1ij ∈ ℝ^p₁ is a vector of fixed effect covariates, Z_1i ∈ ℝ^q₁ is a vector of random effect covariates, σ is the dispersion parameter, β₁ ∈ ℝ^p₁ is a vector of regression coefficients and b_1i ∈ ℝ^q₁ is a vector of random effects. In the Scleroderma example, we use a t distribution with 3 degrees of freedom for residuals, ∊_ij ~ t-distribution with 3 degrees of freedom, to reduce the impact of outlying observations and achieve robust inference. There are various ways to incorporate the t distribution model for robust inferences²⁵. For example, given sufficient data, one can estimate the degree of freedom based on the likelihood method. In this paper, we use a fixed v = 3 degrees of freedom throughout for robust inference. It simplifies the model and computational effort, as recommended in the literature^25,26. The t distribution with 3 degrees of freedom has sufficient long tails and will provide a considerable degree of down-weighting for extreme outliers²⁵. If outlying observations are not of concern, one can use a normal distribution model for the residuals; ∊_ij ∈ N(0, 1).

To model the pattern of intermittent missingness, we use a mixed effects logistic regression model. Let π_ij = Prob(M_ij = 1) be the probability of intermittent missingness for subject i at visit j,

$$\log \left(\frac{{\pi }_{ij}}{1-{\pi }_{ij}}\right)=X_{2ij}{\beta }_2+Z_{2i}{b}_{2i}$$ (2)

where X_2ij ∈ ℝ^p₂ is a vector of fixed effect covariates, Z_2i ∈ ℝ^q₂ is a vector of random effect covariates, β₂ ∈ ℝ^p₂ is a vector of regression coefficients and b_2i ∈ ℝ^q₂ is a vector of random effects.

The hazard of patient dropout due to death or treatment failure is characterized by a proportional hazards frailty model,

$$\begin{array}{cc}\hfill \lambda (t\mid X_{3i},Z_{3i},b_{3i})=& \underset{h\to 0}{\lim }\frac{Prob(t\le T_i<t+h\mid T_i\ge t,X_{3i},Z_{3i},b_{3i})}{h}\hfill \\ \hfill =& {\lambda }_0\left(t\right)\exp (X_{3i}{\beta }_3+Z_{3i}{b}_{3i}),\hfill \end{array}$$ (3)

where λ₀(t) is the baseline hazard function, X_3i ∈ ℝ^p₃ is a vector of fixed effect covariates, Z_3i ∈ ℝ^q₃ is a vector of random effect covariates, β₃ ∈ ℝ^p₃ is a vector of regression coefficients and b_3i ∈ ℝ^q₃ is a vector of random effects.

The latent random effects of the above 3 models, b_i = (b_1i; b_2i; b_3i), are a q₁+q₂+q₃ dimensional vector to capture the unobserved dependence among all observations. We assume that the random effects follow a multivariate normal distribution, b_i ~ N(0, Σ(θ)),

$$\Sigma \left(\theta \right)=\left(\begin{array}{ccc}\hfill {\Sigma }_{11}\hfill & \hfill {\Sigma }_{12}\hfill & \hfill {\Sigma }_{13}\hfill \\ \hfill {\Sigma }_{21}\hfill & \hfill {\Sigma }_{22}\hfill & \hfill {\Sigma }_{23}\hfill \\ \hfill {\Sigma }_{31}\hfill & \hfill {\Sigma }_{32}\hfill & \hfill {\Sigma }_{33}\hfill \end{array}\right)$$ (4)

Combining equations (1), (2),(3), and (4), this joint model implies that missing data from missed visits and study dropouts are non-ignorable missing data. If the missed visits are considered as ignorable, then equation (2) can be removed. Similarly, if missing data dude to study dropouts are ignorable missing data, then equation (3) can be removed. We also note that all fixed effects covariates (X_1ij, X_2ij, X_3i) and random effects covariates (Z_1i, Z_2i, Z_3i) can be disjoint or overlapped.

2.1 Likelihood and estimation

Let Y_obs and Y_mis be the observed and missing outcome measurements, and M_obs and M_mis be the observed and missing indicators for intermittent missingness. The death and treatment failure information S_obs is observed for all subjects. X_i = (X_1i1, …, X_1iK, X_2i1, …, X_2iK, X_3i) and Z_i = (Z_1i, Z_2i, Z_3i) are fixed and random effects covariates of the ith subject. The likelihood function for the ith subject is

$$\begin{array}{cc}\hfill L_i=& \int f({\mathit{Y}}_{i,obs},{\mathit{Y}}_{i,mis},{\mathit{M}}_{i,obs},{\mathit{M}}_{i,mis}{\mathit{S}}_{i,obs})d{\mathit{Y}}_{i,mis}d{\mathit{M}}_{i,mis}d{\mathit{b}}_i\hfill \\ \hfill =& \int f({\mathit{Y}}_{i,obs},{\mathit{Y}}_{i,mis}\mid X_i,Z_i,{\mathit{b}}_i)f({\mathit{M}}_{i,obs},{\mathit{M}}_{i,mis}\mid X_i,Z_i,{\mathit{b}}_i)f({\mathit{S}}_{i,obs}\mid X_i,Z_i,{\mathit{b}}_i)\hfill \\ \hfill \times & f\left({\mathit{b}}_i\right)d{\mathit{Y}}_{i,mis}d{\mathit{M}}_{i,mis}d{\mathit{b}}_i\hfill \end{array}$$

The latent random effects model assumes that the observed data (Y_i,obs, M_i,obs) and the unobserved data (Y_i,obs, M_i,obs) are conditionally independent given the random effects b_i. Furthermore, because ∫ f(Y_i,miss)dY_i,mis = 1 and ∫ f(M_i,miss)dM_i,mis = 1, the likelihood function is the likelihood of observed data:

$$L_i=\int f({\mathit{Y}}_{i,obs}\mid X_i,Z_i,{\mathit{b}}_i)f({\mathit{M}}_{i,obs}\mid X_i,Z_i,{\mathit{b}}_i)f({\mathit{S}}_{i,obs}\mid X_i,Z_i,{\mathit{b}}_i)f\left({\mathit{b}}_i\right)d{\mathit{b}}_i$$

Let ϕ = (β₁, β₂, β₃, σ, θ) and ${\Lambda }_0\left(t\right)={\int }_0^t\lambda \left(u\right)du$. Our goal is to calculate the maximum likelihood estimates for Θ = (ϕ, Λ₀), over a set in which ϕ is in a bounded set and Λ₀ is in a space of all the increasing function in t with Λ₀(0) = 0. Note that the random effects b_i, i ∈ 1, …, N are unobserved and considered as missing data.

Because the maximization is straight forward with complete data, we use the EM algorithm to calculate the maximum likelihood estimates. In the E-step, we calculate the expectation of complete-data log-likelihood given the observed data and the current values of the parameters. More specifically, at the (k+1)th iteration, the E-step consists of evaluating the expected value of functions of b_i with respect to its conditional distribution with parameters estimated in the kth iteration

$$f({\mathit{b}}_i\mid D_i,{\Lambda }^{\left(k\right)},{\varphi }^{\left(k\right)})=\frac{f(D_i,{\mathit{b}}_i\mid {\Lambda }^{\left(k\right)},{\varphi }^{\left(k\right)})}{\int f(D_i,{\mathit{b}}_i\mid {\Lambda }^{\left(k\right)},{\varphi }^{\left(k\right)})d{\mathit{b}}_i}$$

where D_i = (Y_i,obs, M_i,obs, S_i,obs) denotes the observed data of the ith subject, and Λ(^k) and ϕ(^k) are the estimates from the kth iteration. For example, the conditional expectation for function A(b_i),

$$\begin{array}{cc}\hfill & E\left(A\right({\mathit{b}}_i)\mid D_i,{\Lambda }^{\left(k\right)},{\varphi }^{\left(k\right)})=\int A\left({\mathit{b}}_i\right)f({\mathit{b}}_i\mid D_i,{\Lambda }^{\left(k\right)},{\varphi }^{\left(k\right)})d{\mathit{b}}_i\hfill \\ \hfill & =\frac{\int A\left({\mathit{b}}_i\right)f(D_i,{\mathit{b}}_i\mid {\Lambda }^{\left(k\right)},{\varphi }^{\left(k\right)})d{\mathit{b}}_i}{\int f(D_i,{\mathit{b}}_i\mid {\Lambda }^{\left(k\right)},{\varphi }^{\left(k\right)})d{\mathit{b}}_i}\hfill \end{array}$$ (5)

The E steps involves at least 3 dimensional integrations, which demand intensive computation. We use several techniques to reduce computational burden and to achieve better accuracy in evaluating equation (5) in the E step. First of all, we approximate the numerator and denominator separately by Gauss-Hermite quadrature. It has been suggested in the literature^13,27,28 that the two integrands in the numerator and denominator in equation (5) are similar in shape. By taking the ratio of the numerator and denominator, the leading error term in the approximation may cancel out and result in better approximation accuracy. However, the computational burden to evaluate the numerator and denominator in equation (5) can be large even with moderate number of random effects b_i and if many functions A(b_i) are evaluated in the E steps.

Here we use two strategies to reduce the computational burden: to use the Taylor series expansion to approximate E(A(b_i)) and to use adaptive quadrature to increase the computational efficiency. For the first strategy, we use the Taylor series expansion to approximate the expectation in the numerator for all functions A(b_i) by the first two moments of b_i

$$E\left(A\right({\mathit{b}}_i\left)\right)\approx A\left(E{b}_i\right)+\frac{1}{2}{A}^{\left(2\right)}\left(E{b}_i\right)V{b}_i$$

where Eb_i = E(b_i) is the expectation of b_i, V b_i = E(b_i − Eb_i)² is the variance of b_i, and $A^{\left(2\right)}\left(b\right)=\frac{{\partial }^{2}A\left(b\right)}{\partial b^2}$ is the second partial derivative of A(b). With the Taylor series approximation, the only integrals need to be evaluated in the E step are the first two moments of b_i.

We use the Gauss-Hermite quadrature to evaluate the expectation of the first two moments of b_i. The Gaussian quadrature approximates integrals of function with respect to a given kernel by a weighted average of integrand evaluated at predetermined abscissas. For a multi-dimensional integral, the number of abscissas required to achieve the same accuracy rises exponentially as the number of dimensions increases. The adaptive quadrature applies a linear transformation on b_i such that the integrand will be sampled in a suitable range. Following Liu et al.¹⁶, we use Gaussian Hermite quadrature for integrals of the form

$$\int g\left({\mathit{b}}_i\right)d{\mathit{b}}_i=\int h\left({\mathit{b}}_i\right)\psi ({\mathit{b}}_i,\widehat{\mu },\widehat{\sigma })d{\mathit{b}}_i\approx \sum _{k=1}^m\frac{w_k}{\sqrt{\pi }}h(\widehat{\mu }+\sqrt{2}\widehat{\sigma }{x}_k)$$

where $h\left({\mathit{b}}_i\right)=\frac{g\left({\mathit{b}}_i\right)}{\psi ({\mathit{b}}_i,\widehat{\mu },\widehat{\sigma })}$, m is number of nodes, x_k and w_k are the kth node and weight. The critical step for the success of adaptive quadrature is the choice of the importance distribution ψ and its parameters $\widehat{\mu }$ and $\widehat{\sigma }$. It is suggested^16,17 to use the Laplace method to estimate the mode and dispersion of g(b_i) for $\widehat{\mu }$ and $\widehat{\sigma }$. This choice of importance distribution is near optimal, however, it requires to find the importance distribution for every function g. As described above, with Taylor series approximation, we only need to compute the the first two moments of b_i to approximate E(A(b_i)).

We propose to use a single importance distribution to compute the first two moments of b_i. Specially, we recycle the mean and variance calculated in the previous E step as the importance distribution parameters ($\widehat{\mu }$ and $\widehat{\sigma }$) for the evaluation in the current E step. This choice of importance distribution parameters allows us to sample the integrand g(b_i) in a suitable range with minimal cost in computation. Table 1 compares the bias between Gaussian Hermite (GH) quadrature and proposed adaptive Gaussian Hermite (AGH) quadrature. In this comparison, we assume $\widehat{\mu }$ and $\widehat{\sigma }$ are known. Two random variables are considered in this experiment, a normal distribution Normal(1, 2) variable and a standard exponential distribution Exponential(1) variable. The first two moments of random variables are evaluated by both quadratures with number of nodes ranging from 2 to 30. The results suggest that the adaptive Gaussian Hermite (AGH) quadrature has no bias in estimating the first two moments for the normal random variable, while regular Gaussian Hermite quadrature has bias close to zero with 20 nodes. For the standard exponential random variable, the adaptive Gaussian Hermite quadrature can achieve the same accuracy with fewer number of nodes. For example, the adaptive Gaussian Hermite quadrature with 3 nodes has similar accuracy with the regular Gaussian Hermite quadrature with 10 nodes in evaluating the first two moments of standard exponential variable. In general, the bias diminishes as the number of nodes increases for both regular Gaussian Hermite quadrature and adaptive Gaussian Hermite quadrature. However, we also note that the bias is not reduced in estimating E(X) for the Exponential(1) variable when the number nodes increases from 10 to 20 with the adaptive Gaussian Hermite quadrature.

Table 1.

Comparison between Gaussian Hermite (GH) quadrature and proposed adaptive Gaussian Hermite (AGH)quadrature.

Distribution	X ~ N(1, 2)				X ~ Exp(1)
method	GH		AGH		GH		AGH
No of Nodes	E(X)	E(X2)	E(X)	E(X2)	E(X)	E(X2)	E(X)	E(X2)
2	0.14	0.30	1.00	3.00	0.51	0.36	0.56	1.12
3	0.32	0.72	1.00	3.00	0.48	0.58	0.95	1.50
5	0.61	1.54	1.00	3.00	0.68	0.99	0.94	1.75
10	0.93	2.67	1.00	3.00	0.93	1.53	1.02	1.93
20	1.00	2.99	1.00	3.00	0.99	1.86	0.97	1.99
30	1.00	3.00	1.00	3.00	1.00	1.95	1.01	2.00
true value	1.00	3.00	1.00	3.00	1.00	2.00	1.00	2.00

In the M-step, we solve the conditional score equations of the complete data given the observed data. If the longitudinal model is a linear mixed effects model with normal random effects and residuals, the score equations for the regression coefficients have a closed form solution in the M step. However, for the regression coefficients in the mixed effects logistic model, proportional hazard frailty model and the t-distribution longitudinal model, there is no closed form solution and one-step of Newton Raphson is carried out in the M step. We iterate between E- and M- steps until the estimates converge. Appendix A provides the details of our computational algorithm.

To estimate the standard errors, a direct calculation and inversion of the Fisher information matrix²⁹ is not feasible due to the infinite dimensional parameter λ₀. Standard errors are approximated by the inverse of empirical Fisher information of the log profile likelihood with the nonparametric baseline hazard λ₀ being profiled out. It has been suggested³⁰ that the inverse of empirical Fisher information underestimates standard errors and the bootstrap method is recommended to obtain standard error estimates. The bootstrap method requires intensive computation. In our simulation study it appears that this approximation has satisfactory performance on the inference of longitudinal outcomes. However, under-estimation in the standard error is observed for the parameters in the logistic model and proportional hazard model.

3 Scleroderma lung study data analysis

In this section, we demonstrate the use of our proposed model to handle non-monotone and monotone non-ignorable missingness in the analysis of the Scleroderma lung study³¹. The Scleroderma lung study is a multi-center placebo-control double bind randomized study to evaluate the effects of oral cyclophosphamide (CYC) on lung function and other health-related symptoms in patients with evidence of active alveolitis and scleroderma-related interstitial lung disease. In this study, eligible participants received either daily oral cyclophosphamide or matching placebo for 12 months, followed by another year of follow-up without study medication. The primary endpoint of the study is the forced vital capacity (FVC, expressed as a percentage of the predicted value), which is measured at baseline and at three-month intervals throughout the study. One hundred and fifty eight eligible patients underwent randomization, and about 15% of them dropped out of the study before 12 months. About 30% of dropouts are due to death and treatment failures. Intermittent missed visits also occurred during the course of the study. It is likely that the missing data are due to the ineffectiveness of treatment and related to the outcome of interest.

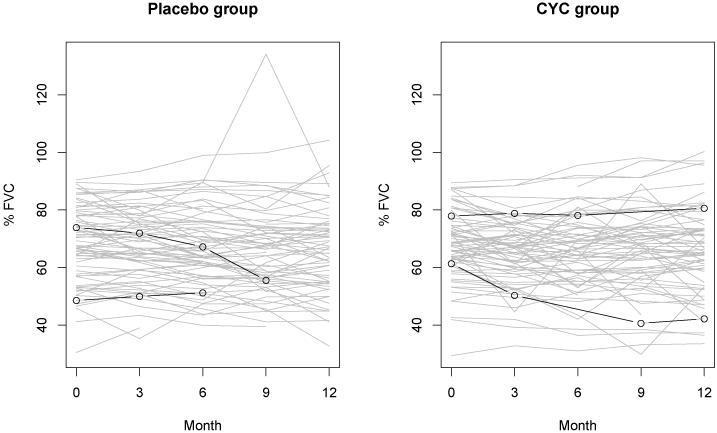
Here we present the analysis of the primary endpoint of FVC. Figure 1 gives the plot of FVC over time for each study group during the first year of the trial. In this figure, two subjects (01-ALS-013 and 04-JWW-010) in the placebo group are highlighted as examples of study dropouts at 6 and 9 months, and two subjects (08-S-L-018 and 09-NEP-005) in the CYC group are examples with missed visits at 6 and 9 months. Most subjects have small variation in FVC over time. However, a few observations show considerable changes between follow-ups. It suggests the possibility of outlying observations. For this analysis, the fixed effects model includes covariates of time, baseline FVC (FVC₀), baseline maximum fibrosis (MAXFIB₀), cyclophosphamide (CYC), and the interactions between treatment and baseline FVC, baseline maximal fibrosis and time. The random effects model includes a random intercept (b₁) which represents the unobserved subject level factor associated with FVC, and residuals (∊) with a t-distribution with 3 degrees of freedom to reduce the impact of outlying observations. σ is related to the variance of FVC.

$$\begin{array}{cc}\hfill \mathrm{FVC}=& {\beta }_0^{\left(1\right)}+{\beta }_1^{\left(1\right)}\text{Time}+{\beta }_2^{\left(1\right)}{\mathrm{FVC}}_0+{\beta }_3^{\left(1\right)}{\mathrm{MAXFIB}}_0+{\beta }_4^{\left(1\right)}\mathrm{CYC}\hfill \\ \hfill & +{\beta }_5^{\left(1\right)}\mathrm{CYC}\times {\mathrm{FVC}}_0+{\beta }_6^{\left(1\right)}\mathrm{CYC}\times {\mathrm{MAXFIB}}_0+{\beta }_7^{\left(1\right)}\mathrm{CYC}\times \text{Time}\hfill \\ \hfill & +b_1+\sigma ∊,\hfill \end{array}$$

For the intermittent missing data model, the mixed effects logistic model is used to model the probability (p) of missed visits. The fixed effect includes time effect and the random effect includes a random intercept (b₂).

$$logit\left(p\right)={\beta }_0^{\left(2\right)}+{\beta }_1^{\left(2\right)}\text{Time}+b_2$$

For time to death or treatment failure, the Proportional hazards frailty model includes covariates of baseline FVC (FVC₀), baseline maximum fibrosis (MAXFIB₀), and cyclophosphamide (CYC). b₃ is the random effect for time to death or treatment failure.

$$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp ({\beta }_1^{\left(3\right)}\mathrm{FVC}+{\beta }_2^{\left(3\right)}{\mathrm{MAXFIB}}_0+{\beta }_3^{\left(3\right)}\mathrm{CYC})+b_3$$

The random effects (b₁, b₂, b₃) in above 3 models are assumed to follow a 3 dimensional multivariate normal distribution to capture the unobserved dependence among FVC measurement, the missed visit events and time to death or treatment failure. Because there are 3 random effects in the joint model, the E steps involve 3 dimensional integration. With a 3 nodes Gaussian Hermite quadrature for each dimension, 27 nodes Gaussian Hermite quadrature is used for the integrations in the E steps.

Figure 1.

Longitudinal FVC in the placebo and CYC groups during the first 12 months. In the Scleroderma lung study, the forced vital capacity (FVC, expressed as a percentage of the predicted value) is measured at baseline and at three-month intervals throughout the study. In this figure, two subjects (01-ALS-013 and 04-JWW-010) in the placebo group are highlighted as examples of study dropouts at 6 and 9 months, and two subjects (08-S-L-018 and 09-NEP-005) in the CYC group are examples of missed visits at 6 and 9 months.

As this is a randomized trial, the assignment of CYC is independent of baseline characteristics. We can derive the overall treatment effect at time m:

$$\begin{array}{cc}\hfill E& (\mathrm{FVC}\mid \mathrm{CYC}=1,\text{Time}=m)-E(\mathrm{FVC}\mid \mathrm{CYC}=0,\text{Time}=m)\hfill \\ \hfill =& \int \left\{E\right(\mathrm{FVC}\mid \mathrm{CYC}=1,\text{Time}=m,{\mathrm{FVC}}_0,{\mathrm{MAXFIB}}_0,b_1)\hfill \\ \hfill -& E(\mathrm{FVC}\mid \mathrm{CYC}=0,\text{Time}=m,{\mathrm{FVC}}_0,{\mathrm{MAXFIB}}_0,b_1)\}\hfill \\ \hfill \times & f({\mathrm{FVC}}_0,{\mathrm{MAXFIB}}_0)d{\mathrm{FVC}}_{0}d{\mathrm{MAXFIB}}_0\hfill \\ \hfill \approx & 1∕n{\Sigma }_{i=1}^n{\mathrm{Eff}}_i\hfill \end{array}$$

where Eff_i is the treatment(CYC) effect for the ith subject at time m

$$\begin{array}{cc}\hfill {\mathrm{Eff}}_i=& E({\mathrm{FVC}}_i\mid \mathrm{CYC}=1,\text{Time}=m,{\mathrm{FVC}}_{0i},{\mathrm{MAXFIB}}_{0i},b_{1i})\hfill \\ \hfill & -E({\mathrm{FVC}}_i\mid \mathrm{CYC}=0,\text{Time}=m,{\mathrm{FVC}}_{0i},{\mathrm{MAXFIB}}_{0i},b_{1i}),\hfill \end{array}$$

Table 2 gives parameter estimates in the longitudinal model for the Scleroderma lung study, based on 6 to 18 months data. We observed that the FVC outcome is associated with baseline FVC measurement and maximum fibrosis score. In addition, the treatment effect appears to be modified by baseline FVC measurement and maximum fibrosis. Roth et al.³² also reported similar findings of the treatment-maximum fibrosis interaction effect using a different analysis. The estimated overall treatment effect is also reported in Table 2.

Table 2.

Analysis of FVC in the Scleroderma study, using data over 6 to 18 months

β	Est.	t model Std	p-value
β1 (Time)	−0.07	0.06	0.297
β2(FVC0)	0.92	0.013	<0.001
β3(MAXFIB0)	−1.62	0.16	<0.001
β4(CYC)	−1.08	1.15	0.416
β5(CYC×FVC0)	0.081	0.019	<0.001
β6(CYC×MAXFIB0)	1.50	0.25	<0.001
β7(CYC×Time)	0.24	0.09	0.009
overall effect at
6 months	0.36	0.71	0.609
9 months	1.08	0.51	0.036
12 months	1.79	0.41	<0.001
15 months	2.50	0.47	<0.001
18 months	3.21	0.69	<0.001
β4 = β5 = β6 = β7 = 0			<0.001

4 Simulation study

In this section, we carry out simulation studies to evaluate the effectiveness of the proposed method. The goal is to examine the amount of bias generated from the likelihood approximation by the Gaussian Hermite quadrature and Taylor series approximation. The simulation set-up includes a linear mixed model to generate longitudinal outcome data, a logistic mixed model for intermittent missing data, and a proportional hazard frailty model for time to dropout due to treatment failure or death.

Here are the specifications of 3 models:

$$Y_{ij}={\beta }_{10}+{\beta }_{11}{X}_{11ij}+b_{1i}+e_{ij},$$ (6)

$$Prob(M_{ij}=1)=\frac{\exp ({\beta }_{20}+{\beta }_{21}{X}_{21ij}+b_{2i})}{1+\exp ({\beta }_{20}+{\beta }_{21}{X}_{21ij}+b_{2i})},$$ (7)

$${\lambda }_i\left(t\right)={\lambda }_0\left(t\right)\exp (X_{31i}{\beta }_{31}+b_{3i}).$$ (8)

Y_ij is the longitudinal outcome value of the ith subject at the jth time i = 1, …, N, j = 1, …, K = 6. The sample size is n, and each subject has at most K = 6 visits including the baseline visit. X_11ij is the longitudinal covariate for the longitudinal outcome the ith subject at the jth time. β₁₁ represents the strength of the association between the outcome Y_ij and X_11ij. For example, if X_11ij is the indicator of treatment assignment, then β₁₁ quantifies the treatment effect. M_ij is the intermittent missing indicator; M_ij = 1 if Y_ij is missing due to missed visits, and 0 if Y_ij is observed. X_21ij is the longitudinal covariate for the intermittent missingness for the ith subject at the jth time. We assume that, for intermittent missed visit, X_21ij is always observed before it is censored by the dropout time or the end of study. β₂₁ indicates the association between missed visit M_ij and X_21ij, and β₂₀ determines the prevalence of intermittent missingness. About 10% visits are missing. Time to death or treatment failure is generated with proportional hazard model with a constant baseline hazard λ₀(t). The censoring time and the baseline hazard are simulated with constant hazard functions, such that about 15% subject are censored (loss to follow-up for other reasons) and p_s = 20% or 50% subjects drop out due to treatment failure or death before finishing 6 follow-up visits. All covariates in the models, X_11ij, X_21ij and X_31i, are generated according to standard normal distribution.

The true values of the regression coefficients are (β₁₀, β₁₁, β₂₁, β₃₁) = (2, 2, 2, 2). The random effect (b₁, b₂, b₃) follows multi-variate normal distribution with mean zero, common variance 2, and correlation 0.5 among the random effects. The residuals of the longitudinal outcome are generated based on a mixture of normal distributions to represent possible outlying observations.

$$e_{ij}~(1-p_e)N(0,{\sigma }_e^2)+p_{e}N(0,f_e^2{\sigma }_e^2),$$

where p_e corresponds to the percent of outlying observations, and f_e > 1 represents the degree that the outliers deviate from rest of the observations. A large f_e generates large variability in the outliers. A special case p_e = 0 gives normal distribution residuals without outliers. In the simulation we vary p_e among 0%, 10% and 25%, set f_e = 4, and vary sample size between n = 200 and 400. Five hundred simulations are carried out for each parameter combination. With 3 random effects in the joint model, the E steps involve 3 dimensional integrations. We use a 3 nodes Gaussian Hermite quadrature for the each dimension, which results in a 3³ = 27 nodes Gaussian Hermite quadrature for the 3 dimensional integrations in the E steps.

Table 3 provides the simulation results. The upper table gives the summary for the estimated regression coefficients in the longitudinal t-distribution model. It suggests that the estimates of β₀₁ and β₁₁ have minimal biases, the estimated standard errors are close to empirical standard deviation of the estimates, and the 95% coverage probability is satisfactory. This results also suggest good performance for the t-distribution model in the presence of outlying observations.

Table 3.

Simulation results with sample sizes N = 200,400. p_s is the propor tion of non-ignorable dropouts due to death and treatment failure. p_e is the proportion of outlying observations in the longitudinal model. β₁₀, β₁₁, β₂₁, and β₃₁ are the average estimates in 500 simulations, with standard deviation in parenthesis. SD is the average estimated standard errors. CP is the coverage probability for the 95% confidence interval. The true values of the regression coefficients are (β₁₀, β₁₁, β₂₁, β₃₁) = (2, 2, 2, 2).

N	ps	pe	β 10	SD(β10)	CP	β 11	SD(β11)	CP
200	0.2	0	2.01 ( 0.14 )	0.13	92 %	2.00 ( 0.09 )	0.08	94 %
		0.10	2.00 ( 0.14 )	0.13	93 %	2.00 ( 0.09 )	0.10	96 %
		0.25	1.99 ( 0.17 )	0.15	92 %	2.00 ( 0.12 )	0.13	95 %
	0.5	0	2.01 ( 0.15 )	0.14	91 %	2.00 ( 0.09 )	0.09	95 %
		0.10	2.02 ( 0.17 )	0.15	93 %	2.01 (0.11)	0.10	92 %
		0.25	2.00 ( 0.19 )	0.17	92 %	2.02 ( 0.12 )	0.13	96 %
400	0.2	0	2.01 ( 0.10 )	0.10	94 %	2.00 ( 0.06 )	0.06	92 %
		0.10	2.01 (0.11)	0.10	94 %	2.00 ( 0.07 )	0.07	93 %
		0.25	2.01 ( 0.12 )	0.11	93 %	2.00 ( 0.08 )	0.08	96 %
	0.5	0	2.02 ( 0.11 )	0.10	93 %	2.00 ( 0.07 )	0.06	93 %
		0.10	2.02 ( 0.12 )	0.11	93 %	2.00 ( 0.08 )	0.07	94 %
		0.25	2.02 ( 0.13 )	0.12	93 %	2.00 ( 0.09 )	0.09	96 %

N	ps	pe	β 21	SD(β21)	CP	β 31	SD(β31)	CP
200	0.2	0	2.00 ( 0.20 )	0.16	92 %	1.93 ( 0.23 )	0.17	82 %
		0.10	2.01 ( 0.20 )	0.17	90 %	1.92 ( 0.24 )	0.17	81 %
		0.25	2.03 ( 0.20 )	0.17	89 %	1.95 ( 0.26 )	0.17	79 %
	0.5	0	2.02 ( 0.21 )	0.18	92 %	1.90 ( 0.22 )	0.14	73 %
		0.10	2.03 ( 0.21 )	0.18	92 %	1.90 ( 0.23 )	0.14	73 %
		0.25	2.03 ( 0.22 )	0.18	91 %	1.89 ( 0.22 )	0.14	73 %
400	0.2	0	2.00 ( 0.14 )	0.11	91 %	1.98 ( 0.18 )	0.12	80 %
		0.10	2.01 ( 0.14 )	0.12	91 %	1.98 ( 0.18 )	0.12	80 %
		0.25	2.01 ( 0.14 )	0.12	91 %	1.97 ( 0.18 )	0.12	79 %
	0.5	0	2.01 ( 0.15 )	0.13	89 %	1.96 ( 0.17 )	0.10	71 %
		0.10	2.02 ( 0.15 )	0.13	90 %	1.95 ( 0.17 )	0.10	73 %
		0.25	2.02 ( 0.15 )	0.13	90 %	1.95 ( 0.17 )	0.10	72 %

The lower table provides the summary for the estimated regression coefficients in the intermittent missing logistic model (β₂₁) and the time to death or treatment failure model (β₃₁). We observe that β₂₁ is generally unbiased or minimally overestimated. A larger sample size (n = 400) appears to further diminish the biases. The standard errors are underestimated, which results in the slightly lower coverage probability ranging from 89% to 92%. Similar to the results in the Laplace approximation^11,12, we observe a relatively large bias in the estimates of β₃₁. A larger sample size (N = 400) appears to reduce the biases. However, the standard error are also underestimated. The 95% coverage probability ranges from 72% to 82%. The underestimation may be due to the approximation of integration with Gaussian Hermite quadrature and the Taylor series approximation of score function. In contrast, the longitudinal outcome in the simulation has a symmetric distribution, which may results in better approximation using Gaussian Hermite quadrature.

Our simulation suggests that the proposed model and our computational method can provide reliable inference for the parameters in the longitudinal model. In some applications, for example the Scleroderma lung study, the primary research interest is the treatment effect on the longitudinal outcome, and the underestimation of the parameters in time to event outcome may not be a big concern.

5 Conclusion

This paper presents a joint model approach to analyze longitudinal outcomes in the presence non-ignorable missing data due to both intermittent and monotone missingness. In the SLS clinical trial example, the intermittent missing data are due to patient missed visits and monotone missing data are from patient dropout due to death or treatment failure. We use a logistic model to describe the intermittent missingness pattern and a Cox proportional model for the dropout due to death or treatment failure. These probabilistic missing models reflect the fact that a subject may come back after missed visits, but will drop out the study if death or treatment failure occurs. Our proposed latent random effects model can easily be extended to models with multiple longitudinal outcomes, multiple intermittent missing outcomes processes, and a competing risk model for multiple causes of dropout. Alternatively, multi-state models are a viable approach to handle both intermittent and monotone missingness simultaneously³³. In a multi state model, one can specifies observed visits, missed visit, death and treatment failure as different states, where missed visits are transient states and death and treatment failure are absorbing states.

We use a t-distribution model to reduce the impact of outlying observations^25,34 in the longitudinal model. It is possible to consider the degrees of freedom as a parameter of the model and estimate it based on the data. One can also extend our model to use a multivariate t distribution to model outcome and random effects simultaneously³⁵. However, this may involve intensive computation, require larger sample size for stable estimation and the improvement in efficiency might be limited. The use of Huber function^36,37 also has been developed for the robust likelihood inference in longitudinal data analysis. Our joint model can easily accommodate the use of Huber function for robust inference.

We develop approximation methods to calculate the maximum likelihood estimates based on adaptive Gaussian Hermite quadrature and Taylor expansion approximation to reduce the computational burden and to improve the approximation accuracy. It will be interesting to compare our approach with other numerical integration methods, such as Laplace approximation^12,13, other adaptive Gaussian Hermite quadrature^16,17, and Monte Carlo integration²⁰. We observe satisfactory performance on the estimates of longitudinal model and logistic regression model. Methods to improve the estimation in the and time to event model warrant further research.

In this paper, standard errors are approximated by the inverse of empirical Fisher information of the log profile likelihood with the nonparametric baseline hazard λ₀ being profiled out. In our simulation study it appears that this approximation has satisfactory performance for the standard error estimation for the longitudinal model. However, under-estimation in the standard error is observed for the parameters in the logistic regression model and proportional hazard model, as suggested in the literature³⁰. Because in the Scleroderma study, the outcome of interest is the longitudinal FVC, our method can provide valid inference; the logistic model and proportional hazard model are incorporated to correct the potential bias due to non-ignorable missing data. Other examples of joint model with the primary interest mostly on longitudinal outcomes include the NINDS rt-PA stroke trial with the main outcome of modified Rankin Scale³⁸ and a breast cancer clinical trial with the quality of life outcome³. On the other hand, when the focus is on the survival outcome, the validity of the standard errors approximated by the inverse of empirical Fisher information may be questionable; for example, HIV clinical trial with patient survival as the outcome⁹ and NYU Women’s Health Study with the outcome of the onset of breast cancer³⁹. The bootstrap method was recommended to obtain standard error estimates³⁰. However, the bootstrap method increases the computational complexity. Other less computationally intensive standard error estimation procedures for semi-parametric models^40,41 in the literature may warrant further investigation.

In contrast to the Laplace approximation, the adaptive quadrature allows to control the error of integration approximation by the number of nodes. We use a fixed 3 nodes adaptive quadrature for each dimension of integration in this paper. It is possible to determine the number of nodes based on the some integration precision criterion. For example, the GLIMMIX procedure in SAS software determines the number of nodes by evaluating the log likelihood at the starting values at a successively larger number of nodes until a tolerance is met. However with a high dimensional integration, different integration function with different dimension (random effect) may require different number of nodes to reach the same precision. In our example, the integration related to the random effect of the Cox proportional hazards model may possibly require more nodes than the integration related to the random effect of the longitudinal model to achieve better efficiency in computation. Further research to determine optimal number of nodes for adaptive quadrature and to investigate the relationship between the number of nodes and the bias in parameter estimation is needed.

Finally, the latent random effects model provides inference for non-ignorable missingness with correlated random effects. However, the non-ignorable assumption is untestable. Fortunately, in a real life data analysis, one can often bring in knowledge and assumptions that are external to the data to provide evidence for missing mechanism. Therefore the non-ignorable missing data analysis must be carried out with great care. It also implies the importance of the information on the causes of missing data in data collection to determine possible missing mechanism. In our Scleroderma example, many missing data are due to lack of treatment efficacy (for example, death or treatment failure), and non-ignorability seems to be a reasonable assumption. In general, local sensitivity analysis can be performed to evaluate the effects of non-ignorability^42,43.

Appendix

Here we provide the detailed proposed computational algorithm for the EM steps to calculate the maximum Likelihood estimates. Let b_i be the (vector of) random effects, and θ(^k) be the (vector of) estimated parameters in the kth EM steps.

1. Start with initial θ⁽⁰⁾

2. For the kth EM step:

   • –
     E step 1: calculate E(b_i|θ(^k)) and $E({\mathit{b}}_i^2\mid {\theta }^{\left(k\right)})$ with Gaussian Hermite quadrature. The importance distribution is set to be normal distribution with the first two moments of E(b_i|θ^k−1)) and variance $E({\mathit{b}}_i^2\mid {\theta }^{(k-1)})$, which are readily available from the kth EM step.
   • –
     E step 2: approximate the expectation E(A(b_i))| θ^(k)) using the Taylor series expansion.

     $$E\left(A\right({\mathit{b}}_i\left)\right)\approx A\left(E{b}_i\right)+\frac{1}{2}{A}^{\left(2\right)}\left(E{b}_i\right)V{b}_i$$

     where Eb_i = E(b_i) is the expectation of b_i, V b_i = E(b_i − Ebi)² is the variance of b_i, and $A^{\left(2\right)}\left(b\right)=\frac{{\partial }^{2}A\left(b\right)}{\partial b^2}$ is the second partial derivative of A(b).
   • –
     M step: use the approximate E(A(b_i)) to solve the conditional score and obtain θ^(k+1)

3. Repeat 2 until convergence

Remarks:

1. ’E step 1’ reduces the computational effort in looking for the importance function in the adaptive Gaussian Hermite quadrature; we use the same importance function for all integrations, and the parameters in the importance function are readily available from previous iteration.

2. ’E step 2’ uses the Taylor series approximation to reduce the number of needed integrations to the first two moments of random effects. The moments estimates are also re-used in the next iteration to construct the importance distribution in ‘E step 1’.