Figure 4. Force (kcal/mol/Å) on Na⁺ (solid triangles) or K⁺ (open squares) ions in the z-direction as they are pulled step-wise through the KcsA channel.

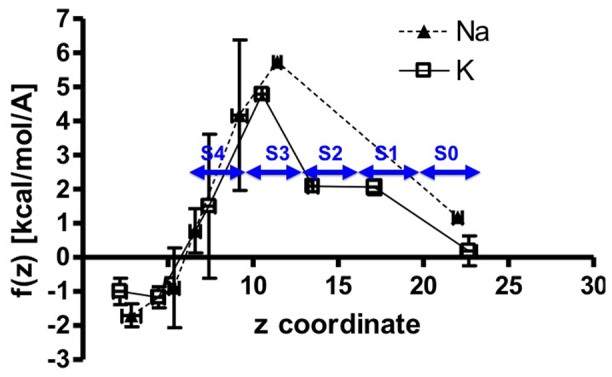
Zero on the z-coordinate axis represents the center of mass of the system. Site S4 in the selectivity filter occurs approximately at z = 7.1 Å, site S3 approximately at z = 10.4 Å, site S2 approximately at z = 13.6 Å, and site S1 approximately at z = 17.0 Å. Histograms of the z positions of each of the two ions were created from all different values of λ (Figure 2). Univariate normal mixture decomposition implemented in STATA (STATA Corp., State College, TX) was used to determine the number of Gaussians that contribute to the complex distribution of each ion distribution in Figure 3. The mean of each Gaussian was associated with a stable position for the ions along the z-axis of the KcsA channel. The 95% confidence interval for each Gaussian was used to partition the force, f(z), to an equal number of segments of normal distributions. Means and standard deviations (SD) for the force were calculated for each segment. Mean values of f(z) are shown in the plot with SD estimates in both z- coordinate and f(z). We define the probability of transition from one stable position to another, P(z_i−>z_i+1), as the probability that the force in the current position, f(z_i), is equal to or larger to the f(z_i+1) in the subsequent position, P(f(z_i)≥f(z_i+1)). Thus, we assume that the transitions between to stable positions of the ions can occur by diffusion or by attraction to the subsequent position without any energy cost. For transitions between two stable points with small SD around the mean f(z), we consider that the probability of transition to the subsequent position is 1 if the mean f(z_i)≥f(z_i+1). Subsequently, the probability for the ion of going back once it reaches stable position z_i+1 is 0. For transitions between stable position of the ion where either the mean for the force, f(z_i), or the subsequent f(z_i+1) has a small SD and the other one has a large SD, we calculate the probability P(f(z_i)≥f(z_i+1)) by focusing on the f(z) with the large SD. Within this given segment for f(z) we calculate the probability as sum of the observations that satisfy the inequality, f(z_i)≥f(z_i+1), divided by the total number of observations within that segment. Finally, for transitions between stable positions of the ion with coordinate z and a f(z) with very large SD, the probability of transition between two positions, P(f(z_i)≥f(z_i+1)), will be represented with P(f(z_i)≥f(z_i+1) ∩ f(z_i+1)≤f(z_i)) = P(f(z_i)≥f(z_i+1)) * P(f(z_i+1)≤f(z_i)). To calculate the two probabilities first find the observations in both segments that satisfy the inequality f(z_i)≥f(z_i+1) and then we divide the respective number by the total number of observations in the given segment. Furthermore, the above formula implies that we consider the two events independent.